2-12 Overflow Detection

"Overflow" means that the result of an arithmetic operation is too large or too small to be correctly represented in the target register. This section discusses methods that a programmer might use to detect when overflow has occurred, without using the machine's "status bits" that are often supplied expressly for this purpose. This is important because some machines do not have such status bits (e.g., MIPS), and because even if the machine is so equipped, it is often difficult or impossible to access the bits from a high-level language.

Signed Add/Subtract

When overflow occurs on integer addition and subtraction, contemporary machines invariably discard the high-order bit of the result and store the low-order bits that the adder naturally produces. Signed integer overflow of addition occurs if and only if the operands have the same sign and the sum has sign opposite to that of the operands. Surprisingly, this same rule applies even if there is a carry into the adder—that is, if the calculation is x + y + 1. This is important for the application of adding multiword signed integers, in which the last addition is a signed addition of two fullwords and a carry-in that may be 0 or +1.

To prove the rule for addition, let x and y denote the values of the one-word signed integers being added, let c (carry-in) be 0 or 1, and assume for simplicity a 4-bit machine. Then if the signs of x and y are different,

or similar bounds apply if x is nonnegative and y is negative. In either case, by adding these inequalities and optionally adding in 1 for c,

This is representable as a 4-bit signed integer, and thus overflow does not occur when the operands have opposite signs.

Now suppose x and y have the same sign. There are two cases:

Thus,

Overflow occurs if the sum is not representable as a 4-bit signed integer?that is, if

In case (a), this is equivalent to the high-order bit of the 4-bit sum being 0, which is opposite to the sign of x and y. In case (b), this is equivalent to the high-order bit of the 4-bit sum being 1, which again is opposite to the sign of x and y.

For subtraction of multiword integers, the computation of interest is x - y - c where again c is 0 or 1, with a value of 1 representing a borrow-in. From an analysis similar to the above, it can be seen that overflow in the final value of x - y - c occurs if and only if x and y have opposite signs and the sign of x - y - c is opposite to that of x (or, equivalently, the same as that of y).

This leads to the following expressions for the overflow predicate, with the result being in the sign position. Following these with a shift right or shift right signed of 31 produces a 1/0- or a -1/0-valued result.

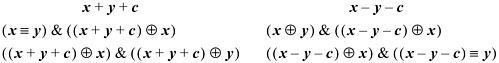
By choosing the second alternative in the first column, and the first alternative in the second column (avoiding the equivalence operation), our basic RISC can evaluate these tests with three instructions in addition to those required to compute x + y + c or x - y - c. A fourth instruction (branch if negative) may be added to branch to code where the overflow condition is handled.

If executing with overflow interrupts enabled, the programmer may wish to test to see if a certain addition or subtraction will cause overflow, in a way that does not cause it. One branch-free way to do this is as follows:

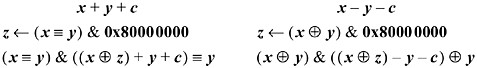
The assignment to z in the left column sets z = 0x80000000 if x and y have the same sign, and sets z = 0 if they differ. Then, the addition in the second expression is done with x and y having different signs, so it can't overflow. If x and y are nonnegative, the sign bit in the second expression will be 1 if and only if (x - 2³¹) + y + c 0—that is, iff x + y + c 2³¹, which is the condition for overflow in evaluating x + y + c. If x and y are negative, the sign bit in the second expression will be 1 iff (x + 2³¹) + y + c < 0—that is, iff x + y + c < -2³¹, which again is the condition for overflow. The term x y ensures the correct result (0 in the sign position) if x and y have opposite signs. Similar remarks apply to the case of subtraction (right column). The code executes in nine instructions on the basic RISC.

It might seem that if the carry from addition is readily available, this might help in computing the signed overflow predicate. This does not seem to be the case. However, one method along these lines is as follows.

If x is a signed integer, then x + 2³¹ is correctly represented as an unsigned number, and is obtained by inverting the high-order bit of x. Signed overflow in the positive direction occurs if x + y 2³¹—that is, if (x + 2³¹) + (y + 2³¹) 3 ?2³¹. This latter condition is characterized by carry occurring in the unsigned add (which means that the sum is greater than or equal to 2³²) and the high-order bit of the sum being 1. Similarly, overflow in the negative direction occurs if the carry is 0 and the high-order bit of the sum is also 0.

This gives the following algorithm for detecting overflow for signed addition:

Compute (x 2³¹) + (y 2³¹), giving sum s and carry c.

Overflow occurred iff c equals the high-order bit of s.

The sum is the correct sum for the signed addition, because inverting the high-order bits of both operands does not change their sum.

For subtraction, the algorithm is the same except that in the first step a subtraction replaces the addition. We assume that the carry is that generated by computing x - y as x + y?/span> + 1. The subtraction is the correct difference for the signed subtraction.

These formulas are perhaps interesting, but on most machines they would not be quite as efficient as the formulas that do not even use the carry bit (e.g., overflow = (x y) & (s x)for addition, and (x y) & (d x)for subtraction, where s and d are the sum and difference, respectively, of x and y).

How the Computer Sets Overflow for Signed Add/Subtract

Machines often set "overflow" for signed addition by means of the logic "the carry into the sign position is not equal to the carry out of the sign position." Curiously, this logic gives the correct overflow indication for both addition and subtraction, assuming the subtraction x - y is done by x + y?/span> + 1. Furthermore, it is correct whether or not there is a carry- or borrow-in. This does not seem to lead to any particularly good methods for computing the signed overflow predicate in software, however, even though it is easy to compute the carry into the sign position. For addition and subtraction, the carry/borrow into the sign position is given by the sign bit after evaluating the following expressions (where c is 0 or 1):

In fact, these expressions give, at each position i, the carry/borrow into position i.

Unsigned Add/Subtract

The following branch-free code may be used to compute the overflow predicate for unsigned add/subtract, with the result being in the sign position. The expressions involving a right shift are probably useful only when it is known that c = 0. The expressions in brackets compute the carry or borrow generated from the least significant position.

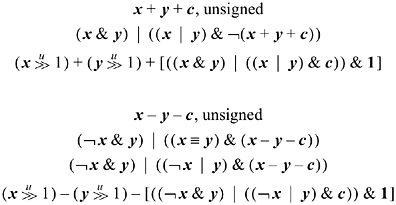
For unsigned add's and subtract's, there are much simpler formulas in terms of comparisons [MIPS]. For unsigned addition, overflow (carry) occurs if the sum is less (by unsigned comparison) than either of the operands. This and similar formulas are given below. Unfortunately, there is no way in these formulas to allow for a variable c that represents the carry- or borrow-in. Instead, the program must test c, and use a different type of comparison depending upon whether c is 0 or 1.

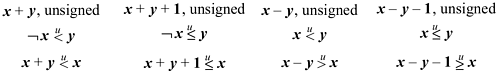
The first formula for each case above is evaluated before the add/subtract that may overflow, and it provides a way to do the test without causing overflow. The second formula for each case is evaluated after the add/subtract that may overflow.

There does not seem to be a similar simple device (using comparisons) for computing the signed overflow predicate.

Multiplication

For multiplication, overflow means that the result cannot be expressed in 32 bits (it can always be expressed in 64 bits, whether signed or unsigned). Checking for overflow is simple if you have access to the high-order 32 bits of the product. Let us denote the two halves of the 64-bit product by hi(x x y) and lo(x x y). Then the overflow predicates can be computed as follows [MIPS]:

One way to check for overflow of multiplication is to do the multiplication and then check the result by dividing. But care must be taken not to divide by 0, and there is a further complication for signed multiplication. Overflow occurs if the following expressions are true:

The complication arises when x = -2³¹ and y = -1. In this case the multiplication overflows, but the machine may very well give a result of -2³¹. This causes the division to overflow, and thus any result is possible (for some machines). Therefore, this case has to be checked separately, which is done by the term y < 0 & x = -2³¹. The above expressions use the "conditional and" operator to prevent dividing by 0 (in C, use the && operator).

It is also possible to use division to check for overflow of multiplication without doing the multiplication (that is, without causing overflow). For unsigned integers, the product overflows iff xy > 2³² - 1, or x > ((2³² - 1)/ y, or, since x is an integer, Expressed in computer arithmetic, this is

For signed integers, the determination of overflow of x * y is not so simple. If x and y have the same sign, then overflow occurs iff xy > 2³¹ - 1. If they have opposite signs, then overflow occurs iff xy < -2³¹. These conditions may be tested as indicated in Table 2-2, which employs signed division.

Table 2-2. Overflow Test for Signed Multiplication
	y > 0	y 0
x > 0	x > 0x7FFFFFFF ?/span> y	y < 0x80000000 ?/span> x
x 0	x < 0x80000000 ?/span> y

This test is awkward to implement because of the four cases. It is difficult to unify the expressions very much because of problems with overflow and with not being able to represent the number +2³¹.

The test can be simplified if unsigned division is available. We can use the absolute values of x and y, which are correctly represented under unsigned integer interpretation. The complete test can then be computed as shown below. The variable c = 2³¹ - 1 if x and y have the same sign, and c = 2³¹ otherwise.

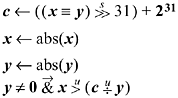
The number of leading zeros instruction may be used to give an estimate of whether or not x * y will overflow, and the estimate may be refined to give an accurate determination. First, consider the multiplication of unsigned numbers. It is easy to show that if x and y, as 32-bit quantities, have m and n leading 0's, respectively, then the 64-bit product has either m + n or m + n + 1 leading 0's (or 64, if either x = 0 or y = 0). Overflow occurs if the 64-bit product has fewer than 32 leading 0's. Hence,

For nlz(x) + nlz(y) = 31, overflow may or may not occur. In this case, the overflow assessment may be made by evaluating This will not overflow. Since xy is 2t or, if y is odd, 2t + x, the product xy overflows if t 2³¹. These considerations lead to a plan for computing xy but branching to "overflow" if the product overflows. This plan is shown in Figure 2-2.

Figure 2-2 Determination of overflow of unsigned multiplication.

unsigned x, y, z, m, n, t; 
 
m = nlz(x); 
n = nlz(y); 
if (m + n <= 30) goto overflow; 
t = x*(y >> 1); 
if ((int)t < 0) goto overflow; 
z = t*2; 
if (y & 1) {
   z = z + x; 
   if (z < x) goto overflow; 
} 
// z is the correct product of x and y. 

For the multiplication of signed integers, we can make a partial determination of whether or not overflow occurs from the number of leading 0's of nonnegative arguments, and the number of leading 1's of negative arguments. Let

Then, we have

There are two ambiguous cases: 32 and 33. The case m + n = 33 overflows only when both arguments are negative and the true product is exactly 2³¹ (machine result is -2³¹), so it can be recognized by a test that the product has the correct sign (that is, overflow occurred if m n (m * n) < 0). When m + n = 32, the distinction is not so easily made.

We will not dwell on this further, except to note that an overflow estimate for signed multiplication can also be made based on nlz(abs(x)) + nlz(abs(y)), but again there are two ambiguous cases (a sum of 31 or 32).

Division

For the signed division x ?y, overflow occurs if the following expression is true:

Most machines signal overflow (or trap) for the indeterminate form 0 ?0.

Straightforward code for evaluating this expression, including a final branch to the overflow handling code, consists of seven instructions, three of which are branches. There do not seem to be any particularly good tricks to improve on this, but below are a few possibilities:

That is, evaluate the large expression in brackets, and branch if the result is less than 0. This executes in about nine instructions, counting the load of the constant and the final branch, on a machine that has the indicated instructions and that gets the "compare to 0" for free.

Some other possibilities are to first compute z from

(three instructions on many machines), and then do the test and branch on y = 0 | z = 0 in one of the following ways:

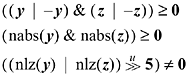
These execute in nine, seven, and eight instructions, respectively, on a machine that has the indicated instructions. The last line represents a good method for PowerPC.

For the unsigned division , overflow occurs if and only if y = 0.