2-17 Multibyte Add, Subtract, Absolute Value

Some applications deal with arrays of short integers (usually bytes or halfwords), and often execution is faster if they are operated on a word at a time. For definiteness, the examples here deal with the case of four 1-byte integers packed into a word, but the techniques are easily adapted to other packings, such as a word containing a 12-bit integer and two 10-bit integers, and so on. These techniques are of greater value on 64-bit machines, because more work is done in parallel.

Addition must be done in a way that blocks the carries from one byte into another. This can be accomplished by the following two-step method:

1. Mask out the high-order bit of each byte of each operand and add (there will then be no carries across byte boundaries).

2. Fix up the high-order bit of each byte with a 1-bit add of the two operands and the carry into that bit.

The carry into the high-order bit of each byte is of course given by the high-order bit of each byte of the sum computed in step 1. The subsequent similar method works for subtraction:

These execute in eight instructions, counting the load of 0x7F7F7F7F, on a machine that has a full set of logical instructions. (Change the and and or of 0x80808080 to and not and or not, respectively, of 0x7F7F7F7F.)

There is a different technique for the case in which the word is divided into only two fields. In this case, addition can be done by means of a 32-bit addition followed by subtracting out the unwanted carry. On page 28 we noted that the expression (x + y) x y gives the carries into each position. Using this and similar observations about subtraction gives the following code for adding/subtracting two halfwords modulo 2¹⁶ (seven instructions):

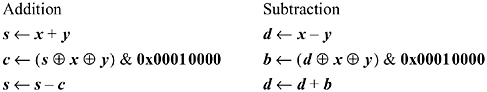
Multibyte absolute value is easily done by complementing and adding 1 to each byte that contains a negative integer (that is, has its high-order bit on). The following code sets each byte of y equal to the absolute value of each byte of x (eight instructions):

The third line could as well be m a + a - b. The addition of b in the fourth line cannot carry across byte boundaries, because the quantity x m has a high-order 0 in each byte.