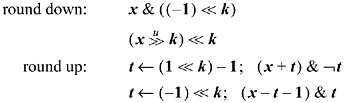3-1 Rounding Up/Down to a Multiple of a Known Power of 2

Rounding an unsigned integer x down to, for example, the next smaller multiple of 8, is trivial: x & -8 does it. An alternative is These work for signed integers as well, provided "round down" means to round in the negative direction (e.g., (-37) & (-8) = -40).

Rounding up is almost as easy. For example, an unsigned integer x can be rounded up to the next greater multiple of 8 with either of

These expressions are correct for signed integers as well, provided "round up" means to round in the positive direction. The second term of the second expression is useful if you want to know how much you must add to x to make it a multiple of 8 [Gold].

To round a signed integer to the nearest multiple of 8 toward 0, you can combine the two expressions above in an obvious way:

An alternative for the first line is which is useful if the machine lacks and immediate, or if the constant is too large for its immediate field.

Sometimes the rounding factor is given as the log₂ of the alignment amount (e.g., a value of 3 means to round to a multiple of 8). In this case, code such as the following may be used, where k = log₂(alignment amount):