4-1 Checking Bounds of Integers

By "bounds checking" we mean to verify that an integer x is within two bounds a and b—that is, that

We first assume that all quantities are signed integers.

An important application is the checking of array indexes. For example, suppose a one-dimensional array A can be indexed by values from 1 to 10. Then, for a reference A(i), a compiler might generate code to check that

and to branch or trap if this is not the case. In this section we show that this check can be done with a single comparison, by performing the equivalent check [PL8]:

This is probably better code, because it involves only one compare-branch (or compare-trap), and because the quantity i - 1 is probably needed anyway for the array addressing calculations.

Does the implementation

always work, even if overflow may occur in the subtractions? It does, provided we somehow know that a b. In the case of array bounds checking, language rules may require that an array not have a number of elements (or number of elements along any axis) that are 0 or negative, and this rule can be verified at compile time or, for dynamic extents, at array allocation time. In such an environment, the transformation above is correct, as we will now show.

It is convenient to use a lemma, which is good to know in its own right.

Lemma. If a and b are signed integers and a b, then the computed value b - a correctly represents the arithmetic value b - a, if the computed value is interpreted as unsigned.

Proof. (Assume a 32-bit machine.) Because a b, the true difference b - a is in the range 0 to (2³¹ - 1) - (-2³¹) = 2³² - 1. If the true difference is in the range 0 to 2³¹ - 1, then the machine result is correct (because the result is representable under signed interpretation), and the sign bit is off. Hence the machine result is correct under either signed or unsigned interpretation.

If the true difference is in the range 2³¹ to 2³² - 1, then the machine result will differ by some multiple of 2³² (because the result is not representable under signed interpretation). This brings the result (under signed interpretation) to the range -2³¹ to -1. The machine result is too low by 2³², and the sign bit is on. Reinterpreting the result as unsigned increases it by 2³², because the sign bit is given a weight of +2³¹ rather than -2³¹. Hence the reinterpreted result is correct.

The "bounds theorem" is

Theorem. If a and b are signed integers and a b, then

Equation 1

Proof. We distinguish three cases, based on the value of x. In all cases, by the lemma, since a b, the computed value b - a is equal to the arithmetic value b - a if b - a is interpreted as unsigned, as it is in Equation (1).

Case 1, x < a: In this case, x - a interpreted as unsigned is x - a + 2³². Whatever the values of x and b are (within the range of 32-bit numbers),

Therefore

and hence

In this case, both sides of Equation (1) are false.

Case 2, a x b: Then, arithmetically, x - a b - a. Because a x, by the lemma x - a equals the computed value x - a if the latter is interpreted as unsigned. Hence

that is, both sides of Equation (1) are true.

Case 3, x > b: Then x - a > b - a. Because in this case x > a (because b > a), by the lemma x - a equals the value of x - a if the latter is interpreted as unsigned. Hence

that is, both sides of Equation (1) are false.

The theorem stated above is also true if a and b are unsigned integers. This is because for unsigned integers the lemma holds trivially, and the above proof is also valid.

Below is a list of similar bounds-checking transformations, with the one of the theorem above stated again. These all hold for either signed or unsigned interpretation of a, b, and x.

Equation 2

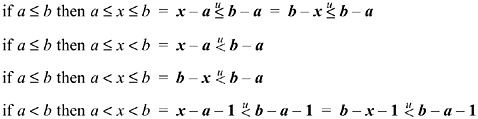
In the last rule, b - a - 1 may be replaced with b + ?span class=docemphbolditalic1>a.

There are some quite different transformations that may be useful when the test is of the form -2^n-1 x 2^n-1 - 1. This is a test to see if a signed quantity x can be correctly represented as an n-bit two's-complement integer. To illustrate with n = 8, the following tests are equivalent:

a.

b.

c.

d.

e.

f.

g.

Equation (b) is simply an application of the preceding material in this section. Equation (c) is as well, after shifting x right seven positions. Equations (c)-(f) and possibly (g) are probably useful only if the constants in Equations (a) and (b) exceed the size of the immediate fields of the computer's compare and add instructions.

Another special case involving powers of 2 is

or, more generally,