4-2 Propagating Bounds through Add's and Subtract's

Some optimizing compilers perform "range analysis" of expressions. This is the process of determining, for each occurrence of an expression in a program, upper and lower bounds on its value. Although this optimization is not a really big winner, it does permit improvements such as omitting the range check on a C "switch" statement and omitting some subscript bounds checks that compilers may provide as a debugging aid.

Suppose we have bounds on two variables x and y as follows, where all quantities are unsigned:

Equation 3

Then, how can we compute tight bounds on x + y, x - y, and -x? Arithmetically, of course, a + c x + y b + d; but the point is that the additions may overflow.

The way to calculate the bounds is expressed in the following:

Theorem. If a, b, c, d, x, and y are unsigned integers and

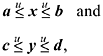
then

Equation 4

Equation 5

Equation 6

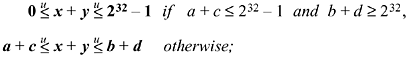
Inequalities (4) say that the bounds on x + y are "normally" a + c and b + d, but if the calculation of a + c does not overflow and the calculation of b + d does overflow, then the bounds are 0 and the maximum unsigned integer. Equations (5) are interpreted similarly, but the true result of a subtraction being less than 0 constitutes an overflow (in the negative direction).

Proof. If neither a + c nor b + d overflows, then x + y with x and y in the indicated ranges, cannot overflow, making the computed results equal to the true results, so the second inequality of (4) holds. If both a + c and b + d overflow, then so also does x + y. Now arithmetically, it is clear that

This, however, is what is calculated when the three terms overflow. Hence in this case also,

If a + c does not overflow but b + d does, then

Because x + y takes on all values in the range a + c to b + d, it takes on the values 2³² - 1 and 2³²—that is, the computed value x + y takes on the values 2³² - 1 and 0 (although it doesn't take on all values in that range).

Lastly, the case that a + c overflows but b + d does not cannot occur, because a b and c d.

This completes the proof of inequalities (4). The proof of (5) is similar, but "overflow" means that a true difference is less than 0.

Inequalities (6) can be proved by using (5) with a = b = 0, and then renaming the variables. (The expression -x with x an unsigned number means to compute the value of 2³² - x, or of ?span class=docemphbolditalic1>x + 1 if you prefer.)

Because unsigned overflow is so easy to recognize (see "Unsigned Add/Subtract" on page 29), these results are easily embodied in code, as shown in Figure 4-1 for addition and subtraction. The computed lower and upper limits are variables s and t, respectively.

Figure 4-1 Propagating unsigned bounds through addition and subtraction operations.

s = a + c;                             s = a - d;
t = b + d;                             t = b - c;
if (s >= a && t < b) {                 if (s > a && t <= b) {
   s = 0;                ?            s = 0;
   t = 0xFFFFFFFF;}                  ?t = 0xFFFFFFFF;}

Signed Numbers

The case of signed numbers is not so clean. As before, suppose we have bounds on two variables x and y as follows, where all quantities are signed:

Equation 7

We wish to compute tight bounds on x + y, x - y, and -x. The reasoning is very similar to that for the case of unsigned numbers, and the results for addition are shown below.

Equation 8

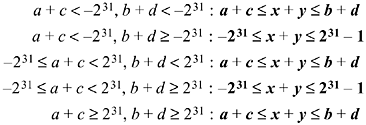
The first row means that if both of the additions a + c and b + d overflow in the negative direction, then the computed sum x + y lies between the computed sums a + c and b + d. This is because all three computed sums are too high by the same amount (2³²). The second row means that if the addition a + c overflows in the negative direction, and the addition b + d either does not overflow or overflows in the positive direction, then the computed sum x + y can take on the extreme negative number and the extreme positive number (although perhaps not all values in between), which is not difficult to show. The other rows are interpreted similarly.

The rules for propagating bounds on signed numbers through the subtraction operation can easily be derived by rewriting the bounds on y as

and using the rules for addition. The results are shown below.

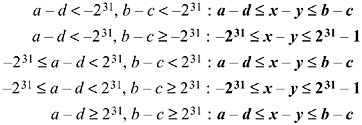
The rules for negation can be derived from the rules for subtraction by taking a = b = 0, omitting some impossible combinations, simplifying, and renaming. The results are as follows:

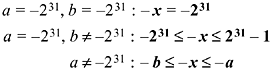
C code for the case of signed numbers is a bit messy. We will consider only addition. It seems to be simplest to check for the two cases in (8) in which the computed limits are the extreme negative and positive numbers. Overflow in the negative direction occurs if the two operands are negative and the sum is nonnegative (see "Signed Add/Subtract" on page 26). Thus, to check for the condition that a + c < -2³¹, we could let s = a + c; and then code something like "if (a < 0 && c < 0 && s >= 0) ?" It will be more efficient, ^[1] however, to perform logical operations directly on the arithmetic variables, with the sign bit containing the true/false result of the logical operations. Then, we write the above condition as "if ((a & c & ~s) < 0) ?" These considerations lead to the program fragment shown in Figure 4-2 below.

^[1] In the sense of more compact, less branchy, code; faster-running code may result from checking first for the case of no overflow, assuming the limits are not likely to be large.

Figure 4-2 Propagating signed bounds through an addition operation.

s = a + c; 
t = b + d; 
u = a & c & ~s & ~(b & d & ~t); 
v = ((a ^ c) | ~(a ^ s)) & (~b & ~d & t); 
if ((u | v) < 0) {
   s = 0x80000000; 
   t = 0x7FFFFFFF;} 

Here u is true (sign bit is 1) if the addition a + c overflows in the negative direction, and the addition b + d does not overflow in the negative direction. Variable v is true if the addition a + c does not overflow and the addition b + d overflows in the positive direction. The former condition can be expressed as "a and c have different signs, or a and s have the same sign." The "if" test is equivalent to "if (u < 0 || v < 0)—that is, if either u or v is true."