5-4 Counting Trailing 0's
If the number of leading zeros instruction is available, then the best way to count trailing 0's is, most likely, to convert it to a count leading 0's problem:
If population count is available, a slightly better method is to form a mask that identifies the trailing 0's, and count the 1-bits in it [Hay2], such as
Variations exist using other expressions for forming a mask that identifies the trailing zeros of x, such as those given in Section 2-1,"Manipulating Rightmost Bits" on page 11. These methods are also reasonable even if the machine has none of the bit-counting instructions. Using the algorithm for pop(x) given in Figure 5-2 on page 66, the first expression above executes in about 3 + 21 = 24 instructions (branch-free).
Figure 5-13 shows
an algorithm that does it directly, in 12 to 20 basic RISC instructions (for x 
0).
Figure 5-13 Number of trailing zeros, binary search.
int ntz(unsigned x) {牋 int n; 牋 if (x == 0) return(32); 牋爊 = 1; 牋爄f ((x & 0x0000FFFF) == 0) {n = n +16; x = x >>16;} 牋爄f ((x & 0x000000FF) == 0) {n = n + 8; x = x >> 8;} 牋爄f ((x & 0x0000000F) == 0) {n = n + 4; x = x >> 4;} 牋爄f ((x & 0x00000003) == 0) {n = n + 2; x = x >> 2;} 牋爎eturn n - (x & 1); }
The n + 16 can be simplified to 17 if that helps, and if the compiler is not smart enough to do that for you (this does not affect the number of instructions as we are counting them).
Figure 5-14 shows a variation that uses smaller immediate values and simpler operations. It executes in 12 to 21 basic RISC instructions. Unlike the above procedure, when the number of trailing 0's is small, the one in Figure 5-14 executes a larger number of instructions, but also a larger number of "fall through" branches.
Figure 5-14 Number of trailing zeros, smaller immediate values.
int ntz(unsigned x) {牋 unsigned y; 牋爄nt n; 牋 if (x == 0) return 32; 牋爊 = 31; 牋爕 = x <<16;?if (y != 0) {n = n -16;?x = y;} 牋爕 = x << 8;?if (y != 0) {n = n - 8;?x = y;} 牋爕 = x << 4;?if (y != 0) {n = n - 4;?x = y;} 牋爕 = x << 2;?if (y != 0) {n = n - 2;?x = y;} 牋爕 = x << 1;?if (y != 0) {n = n - 1;} 牋爎eturn n; }
The line just above the return statement may alternatively be coded
n = n - ((x << 1) >> 31);
which saves a branch, but not an instruction.
In terms of number of instructions executed, it is hard to beat the "search tree" [Aus2]. Figure 5-15 illustrates this procedure for an 8-bit argument. This procedure executes in seven instructions for all paths except the last two (return 7 or 8), which require nine. A 32-bit version would execute in 11 to 13 instructions. Unfortunately, for large word sizes the program is quite large. The 8-bit version above is 12 lines of executable source code and would compile into about 41 instructions. A 32-bit version would be 48 lines and about 164 instructions, and a 64-bit version would be twice that.
Figure 5-15 Number of trailing zeros, binary search tree.
int ntz(char x) {牋 if (x & 15) {牋牋?if (x & 3) {牋牋牋牋 if (x & 1) return 0; 牋牋牋牋爀lse return 1; 牋牋牋} 牋牋牋else if (x & 4) return 2; 牋牋牋else return 3; 牋爙 牋爀lse if (x & 0x30) {牋牋?if (x & 0x10) return 4; 牋牋牋else return 5; 牋爙 牋爀lse if (x & 0x40) return 6; 牋爀lse if (x) return 7; 牋爀lse return 8; }
If the number of trailing 0's is expected to be small or large, then the simple loops below are quite fast. The left-hand algorithm executes in 5 + 3ntz(x) and the right one in 3 + 3(32 - ntz(x)) basic RISC instructions.
Figure 5-16 Number of trailing zeros, simple counting loops.
int ntz(unsigned x) {牋 int n; 牋 x = ~x & (x - 1); 牋爊 = 0;牋牋牋牋牋牋牋牋牋牋牋 // n = 32; 牋爓hile(x != 0) {牋牋?牋牋牋牋// while (x != 0) {牋牋?n = n + 1;牋牋牋牋牋牋牋?//牋?n = n - 1; 牋牋牋x = x >> 1;牋牋牋牋牋牋牋 //牋?x = x + x; 牋爙牋牋牋牋牋牋牋牋牋牋牋牋牋?// } 牋爎eturn n;牋牋牋牋牋牋牋牋牋?// return n; }
It is interesting to note that if the numbers x are uniformly distributed, then the average number of trailing 0's is, very nearly, 1.0. To see this, sum the products pini, where pi is the probability that there are exactly ni trailing 0's. That is,
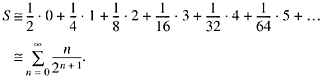
To evaluate this sum, consider the following array:
The sum of each column is a term of the series for S. Hence S is the sum of all the numbers in the array. The sum of the rows are
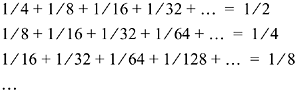
and the sum of these is 1/2 + 1/4 + 1/8 + ?= 1. The absolute convergence of the original series justifies the rearrangement.
Sometimes, a function similar to ntz(x) is wanted, but a 0 argument is a special case, perhaps an error, that should be identified with a value of the function that's easily distinguished from the "normal" values of the function. For example, let us define "the number of factors of 2 in x" to be
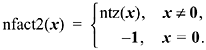
This can be calculated from
Applications
[GLS1] points out some interesting applications of the number of trailing zeros function. It has been named the "ruler function" by Eric Jensen, because it gives the height of a tick mark on a ruler that's divided into halves, quarters, eighths, and so on.
It has an application in R. W. Gosper's loop-detection algorithm, which will now be described in some detail because it is quite elegant and it does more than might at first seem possible.
Suppose a sequence X0, X1, X2, ?is defined by Xn + 1 = f(Xn). If the range of f is finite, the sequence is necessarily periodic. That is, it consists of a leader X0, X1, ? X?- 1 followed by a cycle X?/sub>, Xu + 1, ?span class=docemphasis1>X?+ l - 1 that repeats without limit (X?/sub> = X?+ l, X?+ 1 = X? + l + 1, and so on, where l is the period of the cycle). Given the function f, the loop-detection problem is to find the index m of the first element that repeats, and the period l. Loop detection has applications in testing random number generators and detecting a cycle in a linked list.
One could save all the values of the sequence as they are produced, and compare each new element with all the preceding ones. This would immediately show where the second cycle starts. But algorithms exist that are much more efficient in space and time.
Perhaps the simplest is due to R. W. Floyd [Knu2, sec. 3.1, prob. 6]. This algorithm iterates the process
with x and y initialized to X0. After the nth step, x = Xn and y = X2n. These are compared, and if equal, it is known that Xn and X2n are separated by an integral multiple of the period l梩hat is, 2n - n = n is a multiple of l. Then m can be determined by regenerating the sequence from the beginning, comparing X0 to Xn, then X1 to Xn+1, and so on. Equality occurs when X?/sub> is compared to Xn + ?/sub>. Finally, l can be determined by regenerating more elements, comparing X?/sub> to X?+ 1, X? + 2, ?This algorithm requires only a small and bounded amount of space, but it evaluates f many times.
Gosper's algorithm [HAK, item 132; Knu2, Answers to
Exercises for sec. 3.1, prob. 7] finds the period l, but not the starting
point m of the
first cycle. Its main feature is that it never backs up to reevaluate f, and it is quite economical in space and time. It
is not bounded in space; it requires a table of size log2(L) + 1, where L is the largest possible
period. This is not a lot of space; for example, if it is known a priori that L 
232, then 33 words
suffice.
Gosper's algorithm, coded in C, is shown in Figure 5-17. This
C function is given the function f being
analyzed and a starting value X0. It
returns lower and upper bounds on m, and the period l. (Although Gosper's algorithm cannot compute m, it can compute lower and
upper bounds ml
and mu such that mu - ml + 1 max(l - 1, 1).) The
algorithm works by comparing Xn, for
n = 1, 2, ? to a subset of size 
of
the elements of the sequence that precede Xn.
The elements of the subset are the closest preceding Xi
such that i + 1 ends in a 1-bit (that is, i is the even number preceding n), the closest preceding Xi
such that i + 1 ends in exactly one 0-bit, the
closest preceding Xi such that i + 1 ends in exactly two 0-bits, and so on.
Figure 5-17 Gosper's loop-detection algorithm.
void ld_Gosper(int (*f)(int), int X0, int *mu_l,
牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋int *mu_u, int *lambda) {牋 int Xn, k, m, kmax, n, lgl;
牋爄nt T[33];
牋 T[0] = X0;
牋燲n = X0;
牋爁or (n = 1; ; n++) {牋牋?Xn = f(Xn);
牋牋牋kmax = 31 - nlz(n);牋牋?牋牋?/ Floor(log2 n).
牋牋牋for (k = 0; k <= kmax; k++) {牋牋牋牋 if (Xn == T[k]) goto L;
牋牋牋}
牋牋牋T[ntz(n+1)] = Xn;牋牋牋牋牋牋 // No match.
牋爙
L:
牋?/ Compute m = max{i | i < n and ntz(i+1) = k}. 牋 m = ((((n >> k) - 1) | 1) << k) - 1;
牋?lambda = n - m;
牋爈gl = 31 - nlz(*lambda - 1); // Ceil(log2 lambda) - 1.
牋?span lang=EN-GB>*mu_u = m;牋牋牋牋牋牋牋牋牋牋牋 // Upper bound on mu.
牋?mu_l = m - max(1, 1 << lgl) + 1;// Lower bound on mu. }
Thus, the comparisons proceed as follows:
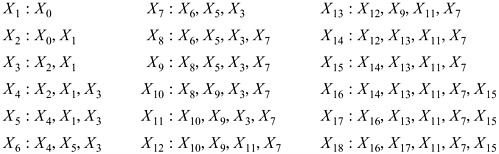
It can be shown that the algorithm always terminates with n somewhere in the second cycle梩hat is, with n < m + 2l. See [Knu2] for further details.
The ruler function reveals how to solve the Tower of Hanoi puzzle. Number the n disks from 0 to n - 1. At each move k, as k goes from 1 to 2n - 1, move disk ntz(k) the minimum permitted distance to the right, in a circular manner.
The ruler function can be used to generate a reflected binary Gray code (see Section 13-1 on page 235). Start with an arbitrary n-bit word, and at each step k, as k goes from 1 to 2n - 1, flip bit ntz(k).