6-1 Find First 0-Byte
The need for this function stems mainly from the way character strings are represented in the C language. They have no explicit length stored with them; instead, the end of the string is denoted by an all-0 byte. To find the length of a string, a C program uses the "strlen" (string length) function. This function searches the string, from left to right, for the 0-byte, and returns the number of bytes scanned, not counting the 0-byte.
A fast implementation of "strlen" might load and test single bytes until a word boundary is reached, and then load a word at a time into a register, and test the register for the presence of a 0-byte. On big-endian machines, we want a function that returns the index of the first 0-byte from the left. A convenient encoding is values from 0 to 3 denoting bytes 0 to 3, and a value of 4 denoting that there is no 0-byte in the word. This is the value to add to the string length, as successive words are searched, if the string length is initialized to 0. On little-endian machines, one wants the index of the first 0-byte from the right end of the register, because little-endian machines reverse the four bytes when a word is loaded into a register. Specifically, we are interested in the following functions, where "00" denotes a 0-byte, "nn" denotes a nonzero byte, and "xx" denotes a byte that may be 0 or nonzero.

Our first procedure for the find leftmost 0-byte function, shown in Figure 6-1, simply tests each byte, in left-to-right order, and returns the result when the first 0-byte is found.
Figure 6-1 Find leftmost 0-byte, simple sequence of tests.
int zbytel(unsigned x) {牋 if牋牋牋牋牋牋 ((x >> 24) == 0) return 0; 牋爀lse if ((x & 0x00FF0000) == 0) return 1; 牋爀lse if ((x & 0x0000FF00) == 0) return 2; 牋爀lse if ((x & 0x000000FF) == 0) return 3; 牋爀lse return 4; }
This executes in two to 11 basic RISC instructions, 11 in the case that the word has no 0-bytes (which is the important case for the "strlen" function). A very similar program will handle the problem of finding the rightmost 0-byte.
Figure 6-2 shows a branch-free procedure for this function. The idea is to convert each 0-byte to 0x80, and each nonzero byte to 0x00, and then use number of leading zeros. This procedure executes in eight instructions if the machine has the number of leading zeros and nor instructions. Some similar tricks are described in [Lamp].
Figure 6-2 Find leftmost 0-byte, branch-free code.
int zbytel(unsigned x) {牋 unsigned y; 牋爄nt n; 牋牋牋牋牋牋牋牋牋牋牋牋?/ Original byte: 00 80 other 牋爕 = (x & 0x7F7F7F7F) + 0x7F7F7F7F;牋 // 7F 7F 1xxxxxxx 牋爕 = ~(y | x | 0x7F7F7F7F);牋牋牋牋牋 // 80 00 00000000 牋爊 = nlz(y) >> 3;牋牋牋牋牋牋 // n = 0 ... 4, 4 if x 牋爎eturn n;牋牋牋牋牋牋牋牋牋?// has no 0-byte. }
The position of the rightmost 0-byte is given by the number of trailing 0's in the final value of y computed above, divided by 8 (with fraction discarded). Using the expression for computing the number of trailing 0's by means of the number of leading zeros instruction (see Section 5- 4, "Counting Trailing 0's," on page 84), this can be computed by replacing the assignment to n in the procedure above with:
n = (32 - nlz(~y & (y - 1))) >> 3;
This is a 12-instruction solution, if the machine has nor and and not.
In most situations on PowerPC, incidentally, a procedure to find the rightmost 0-byte would not be needed. Instead, the words can be loaded with the load word byte-reverse instruction (lwbrx).
The procedure of Figure 6-2 is more valuable on a 64-bit machine than on a 32-bit one, because on a 64-bit machine the procedure (with obvious modifications) requires about the same number of instructions (seven or ten, depending upon how the constant is generated), whereas the technique of Figure 6-1 requires 23 instructions worst case.
If only a test for the presence of a 0-byte is wanted, then a branch on zero (or nonzero) can be inserted just after the second assignment to y.
If the "nlz" instruction is not available, there does not seem to be any really good way to compute the find first 0-byte function. Figure 6-3 shows a possibility (only the executable part of the code is shown).
Figure 6-3 Find leftmost 0-byte, not using nlz.
牋牋牋牋牋牋牋牋牋牋牋 // Original byte: 00 80 other 牋爕 = (x & 0x7F7F7F7F) + 0x7F7F7F7F; // 7F 7F 1xxxxxxx 牋爕 = ~(y | x | 0x7F7F7F7F);牋牋牋牋 // 80 00 00000000 牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋// These steps map: 牋爄f (y == 0) return 4;牋牋牋牋牋牋?// 00000000 ==> 4, 牋爀lse if (y > 0x0000FFFF)牋牋牋牋牋 // 80xxxxxx ==> 0, 牋牋牋return (y >> 31) ^ 1;牋牋牋牋牋 // 0080xxxx ==> 1, 牋爀lse牋牋牋牋牋牋牋牋牋牋牋牋牋牋牋 // 000080xx ==> 2, 牋牋牋return (y >> 15) ^ 3;牋牋牋牋牋 // 00000080 ==> 3.
This executes in ten to 13 basic RISC instructions, ten in the all-nonzero case. Thus, it is probably not as good as the code of Figure 6-1, although it does have fewer branch instructions. It does not scale very well to 64-bit machines, unfortunately.
There are other possibilities for avoiding the "nlz" function. The value of y computed by the code of Figure 6-3 consists of four bytes, each of which is either 0x00 or 0x80. The remainder after dividing such a number by 0x7F is the original value with the up-to-four 1-bits moved and compressed to the four rightmost positions. Thus, the remainder ranges from 0 to 15 and uniquely identifies the original number. For example,

This value can be used to index a table, 16 bytes in size, to get the desired result.
Thus, the code beginning if (y == 0) can be replaced with
static char table[16] = {4, 3, 2, 2, 1, 1, 1, 1, 牋牋牋牋牋牋牋牋牋牋牋牋?, 0, 0, 0, 0, 0, 0, 0}; return table[y%127];
where y is unsigned. The number 31 can be used in place of 127, but with a different table.
These methods involving dividing by 127 or 31 are really just curiosities, because the remainder function is apt to require 20 cycles or more even if directly implemented in hardware. However, below are two more efficient replacements for the code in Figure 6-3 beginning with if (y == 0):
return table[hopu(y, 0x02040810) & 15]; return table[y*0x00204081 >> 28];
Here, hopu(a, b) denotes the high-order 32 bits of the unsigned product of a and b. In the second line, we assume the usual HLL convention that the value of the multiplication is the low-order 32 bits of the complete product. This might be a practical method, if either the machine has a fast multiply or the multiplication by 0x204081 is done by shift-and-add's. It can be done in four such instructions, as suggested by
![]()
Using this 4-cycle way to do the multiplication, the total time for the procedure comes to 13 cycles (7 to compute y, plus 4 for the shift-and-add's, plus 2 for the shift right of 28 and the table index), and of course it is branch-free.
These scale reasonably well to a 64-bit machine. For the "modulus" method, use
return table[y%511];
where table is of size 256, with values 8, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, ?(i.e., table[i] = number of trailing 0's in i).
For the multiplicative methods, use either
return table[hopu(y, 0x0204081020408100) & 255];?or return table[(y*0x0002040810204081?6];
where table is of size 256, with values 8, 7, 6, 6, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4, 3, ?
The multiplication by 0x2 0408 1020 4081 can be done with
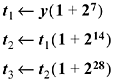
which gives a 13-cycle solution.
All these variations using the table can, of course, implement the find rightmost 0-byte function by simply changing the data in the table.
If the machine does not have the nor instruction, the not in the second assignment to y in Figure 6-3 can be omitted, in the case of a 32-bit machine, by using one of the three return statements given above, with table[i] = 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 4. This scheme does not quite work on a 64-bit machine.
Here is an interesting variation on the procedure of Figure 6-2, again aimed at machines that do not have number of leading zeros. Let a, b, c, and d be 1-bit variables for the predicates "the first byte of x is nonzero," "the second byte of x is nonzero," and so on. Then,
![]()
The multiplications can be done with and's, leading to the procedure shown in Figure 6-4 (only the executable code is shown).
Figure 6-4 Find leftmost 0-byte by evaluating a polynomial.
y = (x & 0x7F7F7F7F) + 0x7F7F7F7F; y = y | x;牋牋牋牋牋 // Leading 1 on nonzero bytes. t1 =?y >> 31;牋牋牋牋牋牋牋 // t1 = a. t2 = (y >> 23) & t1;牋牋牋牋 // t2 = ab. t3 = (y >> 15) & t2;牋牋牋牋 // t3 = abc. t4 = (y >>?7) & t3;牋 牋牋牋// t4 = abcd. return t1 + t2 + t3 + t4;
This comes to 15 instructions on the basic RISC, which is not particularly fast, but there is a certain amount of parallelism. On a superscalar machine that can execute up to three arithmetic instructions in parallel, provided they are independent, it comes to only ten cycles.
A simple variation of this does the find rightmost 0-byte function, based on
![]()
(This requires one more and than the code of Figure 6-4.)
Some Simple Generalizations
Functions "zbytel" and
"zbyter" can be used to search for a byte equal to any particular
value, by first exclusive or'ing the argument x with a word consisting of the desired value
replicated in each byte position. For example, to search x for an ASCII blank (0x20), search x ![]() 0x20202020
for a 0-byte.
0x20202020
for a 0-byte.
Similarly, to search for a byte position in
which two words x and y are equal, search x ![]() y for a 0-byte.
y for a 0-byte.
There is nothing special about byte boundaries in the code of Figure 6-2 and its variants. For example, to search a word for a 0-value in any of the first four bits, the next 12, or the last 16, use the code of Figure 6-2 with the mask replaced by 0x77FF7FFF [PHO]. (If a field length is 1, use a 0 in the mask at that position.)
Searching for a Value in a Given Range
The code of Figure 6-2 can easily be modified to search for a byte in the range 0 to any specified value less than 128. To illustrate, the following code finds the index of the leftmost byte having value from 0 to 9:
y = (x & 0x7F7F7F7F) + 0x76767676; y = y | x; y = y | 0x7F7F7F7F;牋牋牋牋?// Bytes > 9 are 0xFF. y = ~y;牋牋牋牋牋牋牋牋牋牋?// Bytes > 9 are 0x00, 牋牋牋牋牋牋牋牋牋牋牋牋牋牋?/ bytes <= 9 are 0x80. n = nlz(y) >> 3;
More generally, suppose you want to find the leftmost byte in a word that is in the range a to b, where the difference between a and b is less than 128. For example, the uppercase letters encoded in ASCII range from 0x41 to 0x5A. To find the first uppercase letter in a word, subtract 0x41414141 in such a way that the borrow does not propagate across byte boundaries, and then use the above code to identify bytes having value from 0 to 0x19 (0x5A - 0x41). Using the formulas for subtraction given in Section 2-17, "Multibyte Add, Subtract, Absolute Value," on page 36, with obvious simplifications possible with y = 0x41414141, gives
d = (x | 0x80808080) - 0x41414141; d = ~((x | 0x7F7F7F7F) ^ d); y = (d & 0x7F7F7F7F) + 0x66666666; y = y | d; y = y | 0x7F7F7F7F;牋?// Bytes not from 41-5A are FF. y = ~y;牋牋牋牋牋牋牋?// Bytes not from 41-5A are 00, 牋牋牋牋牋牋牋牋牋牋牋?/ bytes from 41-5A are 80. n = nlz(y) >> 3;
For some ranges of values, simpler code exists. For example, to find the first byte whose value is 0x30 to 0x39 (a decimal digit encoded in ASCII), simply exclusive or the input word with 0x30303030 and then use the code given above to search for a value in the range 0 to 9. (This simplification is applicable when the upper and lower limits have n high-order bits in common, and the lower limit ends with 8 - n 0's.)
These techniques can be adapted to handle ranges of 128 or larger with no additional instructions. For example, to find the index of the leftmost byte whose value is in the range 0 to 137 (0x89), simply change the line y = y | x to y = y & x in the code above for searching for a value from 0 to 9.
Similarly, changing the line y = y | d to y = y & d in the code for finding the leftmost byte whose value is in the range 0x41 to 0x5A causes it to find the leftmost byte whose value is in the range 0x41 to 0xDA.