7-1 Reversing Bits and Bytes

By "reversing bits" we mean to reflect the contents of a register about the middle so that, for example,

By "reversing bytes" we mean a similar reflection of the four bytes of a register. Byte reversal is a necessary operation to convert data between the "little-endian" format used by DEC and Intel and the "big-endian" format used by most other manufacturers.

Bit reversal can be done quite efficiently by interchanging adjacent single bits, then interchanging adjacent 2-bit fields, and so on, as shown below [Aus1]. These five assignment statements can be executed in any order.

x = (x & 0x55555555) <<?1 | (x & 0xAAAAAAAA) >>?1; 
x = (x & 0x33333333) <<?2 | (x & 0xCCCCCCCC) >>?2; 
x = (x & 0x0F0F0F0F) <<?4 | (x & 0xF0F0F0F0) >>?4; 
x = (x & 0x00FF00FF) <<?8 | (x & 0xFF00FF00) >>?8; 
x = (x & 0x0000FFFF) << 16 | (x & 0xFFFF0000) >> 16; 

A small improvement results on most machines by using fewer distinct large constants and doing the last two assignments in a more straightforward way, as is shown in Figure 7-1 (30 basic RISC instructions, branch-free).

Figure 7-1 Reversing bits.

unsigned rev(unsigned x) {
   x = (x & 0x55555555) <<?1 | (x >>?1) & 0x55555555; 
   x = (x & 0x33333333) <<?2 | (x >>?2) & 0x33333333; 
   x = (x & 0x0F0F0F0F) <<?4 | (x >>?4) & 0x0F0F0F0F; 
   x = (x << 24) | ((x & 0xFF00) << 8) | 
      ?(x >> 8) & 0xFF00) | (x >> 24); 
   return x; 
} 

The last assignment to x in this code does byte reversal in nine basic RISC instructions. If the machine has rotate shifts, however, this can instead be done in seven instructions with

PowerPC can do the byte-reversal operation in only three instructions [Hay1]: a rotate left of 8, which positions two of the bytes, followed by two "rlwimi" (rotate left word immediate then mask insert) instructions.

Generalized Bit Reversal

[GLS1] suggests that the following sort of generalization of bit reversal, which he calls "flip," is a good candidate to consider for a computer's instruction set:

if (k &?1) x = (x & 0x55555555) <<?1 | (x & 0xAAAAAAAA) >> ?; 
if (k &?2) x = (x & 0x33333333) <<?2 | (x & 0xCCCCCCCC) >>?2; 
if (k &?4) x = (x & 0x0F0F0F0F) <<?4 | (x & 0xF0F0F0F0) >>?4; 
if (k &?8) x = (x & 0x00FF00FF) <<?8 | (x & 0xFF00FF00) >>?8; 
if (k & 16) x = (x & 0x0000FFFF) << 16 | (x & 0xFFFF0000) >> 16; 

(The last two and operations can be omitted.) For k = 31, this operation reverses the bits in a word. For k = 24, it reverses the bytes in a word. For k = 7, it reverses the bits in each byte, without changing the positions of the bytes. For k = 16, it swaps the left and right halfwords of a word, and so on. In general, it moves the bit at position m to position m k. It can be implemented in hardware very similarly to the way a rotate shifter is usually implemented (five stages of MUX's, with each stage controlled by a bit of the shift amount k).

Bit-Reversing Novelties

Item 167 in [HAK] contains rather esoteric expressions for reversing 6-, 7-, and 8-bit integers. Although these expressions are designed for a 36-bit machine, the one for reversing a 6-bit integer works on a 32-bit machine, and those for 7- and 8-bit integers work on a 64-bit machine. These expressions are as follows:

The result of all these is a "clean" integer—right-adjusted with no unused high-order bits set.

In all these cases the "remu" function can instead be "rem" or "mod," because its arguments are positive. The remainder function is simply summing the digits of a base 256 or base 1024 number, much like casting out nines. Hence it can be replaced with a multiply and a shift right. For example, the 6-bit formula has the following alternative on a 32-bit machine (the multiplication must be modulo 2³²):

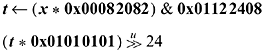
These formulas are limited in their utility because they involve a remaindering operation (20 cycles or more) and/or some multiplications, as well as loading of large constants. The formula immediately above requires ten basic RISC instructions, two of which are multiply's, which amounts to about 20 cycles on a present-day RISC. On the other hand, an adaptation of the code of Figure 7-1 to reverse 6-bit integers requires about 15 instructions, and probably about 9 to 15 cycles, depending on the amount of instruction-level parallelism in the machine. These techniques, however, do give compact code. Below are a few more techniques that might possibly be useful, all for a 32-bit machine. They involve a sort of double application of the idea from [HAK], to extend the technique to 8- and 9-bit integers on a 32-bit machine.

The following is a formula for reversing an 8-bit integer:

Here the "remu" cannot be changed to a multiply and shift. (You have to work these out, and look at the bit patterns, to see why.)

Here is a similar formula for reversing an 8-bit integer, which is interesting because it can be simplified quite a bit:

The simplifications are that the second product is just a shift left of the first product, the last mask can be generated from the second with just one instruction (shift), and the remainder can be replaced by a multiply and shift. It simplifies to 14 basic RISC instructions, two of which are multiply's:

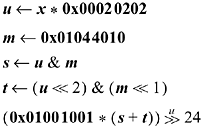
The following is a formula for reversing a 9-bit integer:

The second multiplication can be avoided because the product is equal to the first product shifted right six positions. The last mask is equal to the second mask shifted right eight positions. With these simplifications, this requires 12 basic RISC instructions, including the one multiply and one remainder. The remainder operation must be unsigned, and it cannot be changed to a multiply and shift.

The reader who studies these marvels will be able to devise similar code for other bit-permuting operations. As a simple (and artificial) example, suppose it is desired to extract every other bit from an 8-bit quantity, and compress the four bits to the right. That is, the desired transformation is

0000 0000 0000 0000 0000 0000 abcd efgh ==> 
0000 0000 0000 0000 0000 0000 0000 bdfh 

This may be computed as follows:

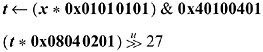
On most machines, the most practical way to do all these operations is by indexing into a table of 1-byte (or 9-bit) integers.

Incrementing a Reversed Integer

The Fast Fourier Transform (FFT) algorithm employs an integer i and its bit reversal rev(i) in a loop in which i is incremented by 1 [PB]. Straightforward coding would increment i and then compute rev(i) on each loop iteration. For small integers, computing rev(i) by table lookup is fast and practical. For large integers, however, table lookup is not practical and, as we have seen, computing rev(i) requires some 29 instructions.

If table lookup cannot be used, it is more efficient to maintain i in both normal and bit-reversed forms, incrementing them both on each loop iteration. This raises the question of how best to increment an integer that is in a register in reversed form. To illustrate, on a 4-bit machine we wish to successively step through the values (in hexadecimal)

0, 8, 4, C, 2, A, 6, E, 1, 9, 5, D, 3, B, 7, F. 

In the FFT algorithm, i and its reversal are both some specific number of bits in length, almost certainly less than 32, and they are both right-justified in the register. However, we assume here that i is a 32-bit integer. After adding 1 to the reversed 32-bit integer, a shift right of the appropriate number of bits will make the result usable by the FFT algorithm (both i and rev(i) are used to index an array in memory).

The straightforward way to increment a reversed integer is to scan from the left for the first 0-bit, set it to 1, and set all bits to the left of it (if any) to 0's. One way to code this is

unsigned x, m; 
 
m = 0x80000000; 
x = x ^ m; 
if ((int)x >= 0) {
   do {
    ?m = m >> 1; 
      x = x ^ m; 
   } while (x < m); 
} 

This executes in three basic RISC instructions if x begins with a 0-bit, and four additional instructions for each loop iteration. Because x begins with a 0-bit half the time, with 10 (binary) one-fourth of the time, and so on, the average number of instructions executed is approximately

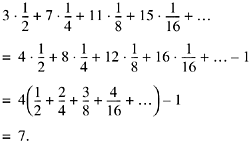
(In the second line we added and subtracted 1, with the first 1 in the form 1/2 + 1/4 + 1/8 + 1/16 + ? This makes the series similar to the one analyzed on page 86.) The number of instructions executed in the worst case, however, is quite large (131).

If number of leading zeros is available, adding 1 to a reversed integer may be done as follows:

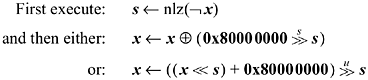
Either method requires five full RISC instructions and, to properly wrap around from 0xFFFFFFFF to 0, requires that the shifts be modulo 64. (These formulas fail in this respect on the Intel x86 machines, because the shifts are modulo 32.)