7-3 Transposing a Bit Matrix

The transpose of a matrix A is a matrix whose columns are the rows of A and whose rows are the columns of A. Here we consider the problem of computing the transpose of a bit matrix whose elements are single bits that are packed eight per byte, with rows and columns beginning on byte boundaries. This seemingly simple transformation is surprisingly costly in instructions executed.

On most machines it would be very slow to load and store individual bits, mainly due to the code that would be required to extract and (worse yet) to store individual bits. A better method is to partition the matrix into 8x8 submatrices, load each 8x8 submatrix into registers, compute the transpose of the submatrix in registers, and then store the 8x8 result in the appropriate place in the target matrix. This section first discusses the problem of computing the transpose of the 8x8 submatrix.

It doesn't matter whether the matrix is stored in row-major or column-major order; computing the transpose consists of the same operations in either event. Assuming for discussion that it's in row-major order, an 8x8 submatrix is loaded into eight registers with eight load byte instructions, addressing a column of the source matrix. That is, the addresses referenced by the load byte instructions are separated by multiples of the source matrix width in bytes. After the transpose of the 8x8 submatrix is computed, it is stored in a column of the target matrix—that is, it is stored with eight store byte instructions into locations separated by multiples of the width of the target matrix in bytes (which is different from the width of the source matrix if the matrices are not square). Thus, we are given eight 8-bit quantities right-justified in registers a0, a1, ? a7, and we wish to compute eight 8-bit quantities right-justified in registers b0, b1, ? b7, for use in the store byte instructions. This is illustrated below, where each digit and letter represents a single bit. Notice that we consider the main diagonal to run from bit 7 of byte 0 to bit 0 of byte 7. Some readers with a little-endian background may be accustomed to thinking of the main diagonal as running from bit 0 of byte 0 to bit 7 of byte 7.

a0 = 0123 4567           b0 = 08go wEMU 
a1 = 89ab cdef           b1 = 19hp xFNV 
a2 = ghij klmn           b2 = 2aiq yGOW 
a3 = opqr stuv  ?==>  ?b3 = 3bjr zHPX 
a4 = wxyz ABCD           b4 = 4cks AIQY 
a5 = EFGH IJKL           b5 = 5dlt BJRZ 
a6 = MNOP QRST           b6 = 6emu CKS$ 
a7 = UVWX YZ$.    ?     b7 = 7fnv DLT. 

The straightforward code for this problem is to select and place each result bit individually, as follows. The multiplications and divisions represent left and right shifts, respectively.

b0 = (a0 & 128)  ?| (a1 & 128)/2?| (a2 & 128)/4?| (a3 & 128)/8 | 
    ?a4 & 128)/16 | (a5 & 128)/32 | (a6 & 128)/64 | (a7    ?)/128; 
b1 = (a0 &?64)*2?| (a1 &?64)  ?| (a2 &?64)/2?| (a3 &?64)/4 | 
    ?a4 &?64)/8?| (a5 &?64)/16 | (a6 &?64)/32 | (a7 &?64)/64; 
b2 = (a0 &?32)*4?| (a1 &?32)*2?| (a2 &?32)  ?| (a3 &?32)/2 | 
    ?a4 &?32)/4?| (a5 &?32)/8?| (a6 &?32)/16 | (a7 &?32)/32; 
b3 = (a0 &?16)*8?| (a1 &?16)*4?| (a2 &?16)*2?| (a3 &?16)   | 
    ?a4 &?16)/2?| (a5 &?16)/4?| (a6 &?16)/8?| (a7 &?16)/16; 
b4 = (a0 &   8)*16 | (a1 &   8)*8?| (a2 &   8)*4?| (a3 &   8)*2 | 
    ?a4 &   8)  ?| (a5 &   8)/2?| (a6 &   8)/4?| (a7 &   8)/8; 
b5 = (a0 &   4)*32 | (a1 &   4)*16 | (a2 &   4)*8?| (a3 &   4)*4 | 
    ?a4 &   4)*2?| (a5 &   4)  ?| (a6 &   4)/2  | (a7 &   4)/4; 
b6 = (a0 &   2)*64 | (a1 &   2)*32 | (a2 &   2)*16 | (a3 &   2)*8 | 
    ?a4 &   2)*4?| (a5 &   2)*2?| (a6 &   2)  ?| (a7 &   2)/2; 
b7 = (a0    ?)*128| (a1 &   1)*64 | (a2 &   1)*32 | (a3 &   1)*16| 
    ?a4 &   1)*8?| (a5 &   1)*4?| (a6 &   1)*2?| (a7 &   1); 

This executes in 174 instructions on most machines (62 and's, 56 shift's, and 56 or's). The or's can of course be add's. On PowerPC it can be done, perhaps surprisingly, in 63 instructions (seven move register's and 56 rotate left word immediate then mask insert's). We are not counting the load byte and store byte instructions, nor their addressing code.

Although there does not seem to be a really great algorithm for this problem, the method to be described beats the straightforward method by more than a factor of 2 on a basic RISC machine.

First, treat the 8x8-bit matrix as 16 2x2-bit matrices, and transpose each of the 16 2x2-bit matrices. Second, treat the matrix as four 2x2 submatrices whose elements are 2x2-bit matrices and transpose each of the four 2x2 submatrices. Finally, treat the matrix as a 2x2 matrix whose elements are 4x4-bit matrices, and transpose the 2x2 matrix. These transformations are illustrated below.

0123 4567     082a 4c6e     08go 4cks     08go wEMU 
89ab cdef     193b 5d7f     19hp 5dlt     19hp xFNV 
ghij klmn     goiq ksmu     2aiq 6emu     2aiq yGOW 
opqr stuv     hpjr ltnv     3bjr 7fnv     3bjr zHPX 
          ==>           ==>           ==> 
wxyz ABCD     wEyG AICK     wEMU AIQY     4cks AIQY 
EFGH IJKL     xFzH BJDL     xFNV BJRZ     5dlt BJRZ 
MNOP QRST     MUOW QYS$     yGOW CKS$     6emu CKS$ 
UVWX YZ$.     NVPX RZT.     zHPX DLT.     7fnv DLT. 

Rather than carrying out these steps on the eight individual bytes in eight registers, a net improvement results from first packing the bytes four to a register, performing the bit-swaps on the two registers, and then unpacking. A complete procedure is shown in Figure 7-2. Parameter A is the address of the first byte of an 8x8 submatrix of the source matrix, which is of size 8mx8n bits. Similarly, parameter B is the address of the first byte of an 8x8 submatrix in the target matrix, which is of size 8nx8m bits. That is, the full source matrix is 8mxn bytes, and the full target matrix is 8nxm bytes.

Figure 7-2 Transposing an 8x8-bit matrix.

void transpose8(unsigned char A[8], int m, int n, 
                unsigned char B[8]) {
   unsigned x, y, t; 
 
   // Load the array and pack it into x and y. 
 
   x = (A[0]<<24)   | (A[m]<<16)   | (A[2*m]<<8) | A[3*m]; 
   y = (A[4*m]<<24) | (A[5*m]<<16) | (A[6*m]<<8) | A[7*m]; 
 
 t = (x ^ (x >> 7)) & 0x00AA00AA;?x = x ^ t ^ (t << 7); 
  ?span
lang=EN-GB>t = (y ^ (y >> 7)) & 0x00AA00AA;?y = y ^ t ^ (t << 7); 
 
   t = (x ^ (x >>14)) & 0x0000CCCC;?x = x ^ t ^ (t <<14); 
   t = (y ^ (y >>14)) & 0x0000CCCC;?y = y ^ t ^ (t <<14); 
 
   t = (x & 0xF0F0F0F0) | ((y >> 4) & 0x0F0F0F0F); 
   y = ((x << 4) & 0xF0F0F0F0) | (y & 0x0F0F0F0F); 
   x = t; 
 
   B[0]=x>>24;  ?B[n]=x>>16;  ?B[2*n]=x>>8;?B[3*n]=x; 
   B[4*n]=y>>24;?B[5*n]=y>>16;?B[6*n]=y>>8;?B[7*n]=y; 
} 

The line

t = (x ^ (x >> 7)) & 0x00AA00AA;?x = x ^ t ^ (t << 7); 

is quite cryptic, for sure. It is swapping bits 1 and 8 (counting from the right), 3 and 10, 5 and 12, and so on, in word x, while not moving bits 0, 2, 4, and so on. The swaps are done with the exclusive or method of bit swapping, described on page 40. Word x, before and after the first round of swaps, is

0123 4567 89ab cdef ghij klmn opqr stuv 
082a 4c6e 193b 5d7f goiq ksmu hpjr ltnv 

To get a realistic comparison of these methods, the naive method described on page 109 was filled out into a complete program similar to that of Figure 7-2. Both were compiled with the GNU C compiler to a target machine that is very similar to the basic RISC. The resulting number of instructions, counting all load's, store's , addressing code, prologs, and epilogs, is 219 for the naive code and 101 for Figure 7-2. (The prologs and epilogs were null, except for a return branch instruction.) A version of the code of Figure 7-2 adapted to a 64-bit basic RISC (in which x and y would be held in the same register) would be about 85 instructions.

The algorithm of Figure 7-2 runs from fine to coarse granularity, based on the lengths of the groups of bits that are swapped. The method can also be run from coarse to fine granularity. To do this, first treat the 8x8-bit matrix as a 2x2 matrix whose elements are 4x4-bit matrices, and transpose the 2x2 matrix. Then treat each the four 4x4 submatrices as a 2x2 matrix whose elements are 2x2-bit matrices, and transpose each of the four 2x2 submatrices, and so on. The code for this is the same as that of Figure 7-2 except with the three groups of statements that do the bit-rearranging run in reverse order.

Transposing a 32x32-Bit Matrix

The same recursive technique that was used for the 8x8-bit matrix can of course be used for larger matrices. For a 32x32-bit matrix it takes five stages.

The details are quite different from Figure 7-2 because here we assume that the entire 32x32-bit matrix does not fit in the general register space, and we seek a compact procedure that indexes the appropriate words of the bit matrix to do the bit swaps. The algorithm to be described works best if run from coarse to fine granularity.

In the first stage, treat the matrix as four 16x16-bit matrices, and transform it as follows:

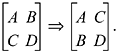
A denotes the left half of the first 16 words of the matrix, B denotes the right half of the first 16 words, and so on. It should be clear that the above transformation may be accomplished by the following swaps:

Right half of word 0 with the left half of word 16,

Right half of word 1 with the left half of word 17,

?/p>

Right half of word 15 with the left half of word 31.

To implement this in code, we will have an index k that ranges from 0 to 15. In a loop controlled by k, the right half of word k will be swapped with the left half of word k + 16.

In the second stage, treat the matrix as 16 8x8-bit matrices, and transform it as follows:

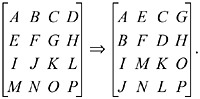
This transformation may be accomplished by the following swaps:

Bits 0x00FF00FF of word 0 with bits 0xFF00FF00 of word 8,

Bits 0x00FF00FF of word 1 with bits 0xFF00FF00 of word 9, and so on.

This means that bits 0-7 (the least significant eight bits) of word 0 are swapped with bits 8-15 of word 8, and so on. The indexes of the first word in these swaps are k = 0, 1, 2, 3, 4, 5, 6, 7, 16, 17, 18, 19, 20, 21, 22, 23. A way to step k through these values is

In the loop controlled by k, bits of word k are swapped with bits of word k +8.

Similarly, the third stage does the following swaps:

Bits 0x0F0F0F0F of word 0 with bits 0xF0F0F0F0 of word 4,

Bits 0x0F0F0F0F of word 1 with bits 0xF0F0F0F0 of word 5, and so on.

The indexes of the first word in these swaps are k = 0, 1, 2, 3, 8, 9, 10, 11, 16, 17, 18, 19, 24, 25, 26, 27. A way to step k through these values is

In the loop controlled by k, bits of word k are swapped with bits of word k + 4.

These considerations are coded rather compactly in the C function shown in Figure 7-3 [GLS1]. The outer loop controls the five stages, with j taking on the values 16, 8, 4, 2, and 1. It also steps the mask m through the values 0x0000FFFF, 0x00FF00FF, 0x0F0F0F0F, 0x33333333, and 0x55555555. (The code for this, m = m ^ (m << j), is a nice little trick. It does not have an inverse, which is the main reason this code works best for coarse to fine transformations.) The inner loop steps k through the values described above. The inner loop body swaps the bits of a [k] identified by mask m with the bits of a [k+j] shifted right j and identified by m, which is equivalent to the bits of a [k+j] identified with the complement of m. The code for performing these swaps is an adaptation of the "three exclusive or" technique shown on page 39 column (c).

Figure 7-3 Compact code for transposing a 32x32-bit matrix.

void transpose32(unsigned A[32]) {
   int j, k; 
   unsigned m, t; 
 
   m = 0x0000FFFF; 
   for (j = 16; j != 0; j = j >> 1, m = m ^ (m << j)) {
    ?for (k = 0; k < 32; k = (k + j + 1) & ~j) {
         t = (A[k] ^ (A[k+j] >> j)) & m; 
         A[k] = A[k] ^ t; 
         A[k+j] = A[k+j] ^ (t << j); 
      } 
   } 
} 

Based on compiling this function with the GNU C compiler to a machine very similar to the basic RISC, this compiles into 31 instructions, with 20 in the inner loop and 7 in the outer loop but not in the inner loop. Thus, it executes in 4 + 5(7 + 16 ?20) = 1639 instructions. In contrast, if this function were performed using 16 calls on the 8x8 transpose program of Figure 7-2, then it would take 16(101 + 5) = 1696 instructions, assuming the 16 calls are "strung out." This includes five instructions for each function call (observed in compiled code). Thus, the two methods are, on the surface anyway, very nearly equal in execution time.

On the other hand, for a 64-bit machine the code of Figure 7-3 can easily be modified to transpose a 64x64-bit matrix, and it would take about 4 + 6(7 + 32 ?20) = 3886 instructions. Doing the job with 64 executions of the 8x8 transpose method would take about 64(85 + 5) = 5760 instructions.

The algorithm works in place, and thus if it is used to transpose a larger matrix, additional steps are required to move 32x32-bit submatrices. It can be made to put the result matrix in an area distinct from the source matrix by separating out either the first or last execution of the "for j-loop" and having it store the result in the other area.

About half the instructions executed by the function of Figure 7-3 are for loop control, and the function loads and stores the entire matrix five times. Would it be reasonable to reduce this overhead by unrolling the loops? It would, if you are looking for the ultimate in speed, if memory space is not a problem, if your machine's I-fetching can keep up with a large block of straight-line code, and, especially if the branches or loads are costly in execution time. The bulk of the program will be the six instructions that do the bit swaps repeated 80 times (5 ?16). In addition, the program will need 32 load instructions to load the source matrix and 32 store instructions to store the result, for a total of at least 544 instructions.

Our GNU C compiler will not unroll loops by such large factors (16 for the inner loop, five for the outer loop). Figure 7-4 outlines a program in which the unrolling is done by hand. This program is shown as not working in place, but it executes correctly in place, if that is desired, by invoking it with identical arguments. The number of "swap" lines is 80. Our GNU C compiler for the basic RISC machine compiles this into 576 instructions (branch-free, except for the function return), counting prologs and epilogs. This machine does not have the store multiple and load multiple instructions, but it can save and restore registers two at a time with store double and load double instructions.

Figure 7-4 Straight-line code for transposing a 32x32-bit matrix.

#define swap(a0, a1, j, m) t = (a0 ^ (a1 >>j)) & m; \ 
                           a0 = a0 ^ t; \ 
                           a1 = a1 ^ (t << j); 
 
void transpose32(unsigned A[32], unsigned B[32]) {
   unsigned m, t; 
   unsigned a0, a1, a2, a3, a4, a5, a6, a7, 
            a8, a9, a10, a11, a12, a13, a14, a15, 
            a16, a17, a18, a19, a20, a21, a22, a23, 
            a24, a25, a26, a27, a28, a29, a30, a31; 
 
   a0?= A[ 0];?a1?= A[ 1];?a2?= A[ 2];?a3?= A[ 3]; 
   a4?= A[ 4];?a5?= A[ 5];?a6?= A[ 6];?a7?= A[ 7]; 
  ?.. 
   a28 = A[28];?a29 = A[29];?a30 = A[30];?a31 = A[31]; 
 
   m = 0x0000FFFF; 
   swap(a0,?a16, 16, m) 
   swap(a1,?a17, 16, m) 
  ?.. 
   swap(a15, a31, 16, m) 
   m = 0x00FF00FF; 
   swap(a0,?a8,   8, m) 
   swap(a1,?a9,   8, m) 
  ?.. 
  ?.. 
   swap(a28, a29,?1, m) 
   swap(a30, a31,?1, m) 
 
   B[ 0] = a0;   B[ 1] = a1;   B[ 2] = a2;   B[ 3] = a3; 
   B[ 4] = a4;   B[ 5] = a5;   B[ 6] = a6;   B[ 7] = a7; 
  ?.. 
   B[28] = a28;?B[29] = a29;?B[30] = a30;?B[31] = a31; 
} 

There is a way to squeeze a little more performance out of this if your machine has a rotate shift instruction (either left or right). The idea is to replace all the swap operations of Figure 7-4, which take six instructions each, with simpler swaps that do not involve a shift, which take four instructions each (use the swap macro given, with the shifts omitted).

First, rotate right words A [16..31] (that is, A [k] for 16 k 31) by 16 bit positions. Second, swap the right halves of A[0] with A[16], A[1] with A[17], and so on, similarly to the code of Figure 7-4. Third, rotate right words A[0..8] and A[24..31] by eight bit positions, and then swap the bits indicated by a mask of 0x00FF00FF in words A[0] and A[8], A[1] and A[9], and so on, as in the code of Figure 7-4. After five stages of this, you don't quite have the transpose. Finally, you have to rotate left word A[1] by one bit position, A[2] by two bit positions, and so on (31 instructions). We do not show the code, but the steps are illustrated below for a 4x4-bit matrix.

The bit-rearranging part of the program of Figure 7-4 requires 480 instructions (80 swaps at six instructions each). The revised program, using rotate instructions, requires 80 swaps at four instructions each, plus 80 rotate instructions (16 ?5) for the first five stages, plus a final 31 rotate instructions, for a total of 431 instructions. The prolog and epilog code would be unchanged, so using rotate instructions in this way saves 49 instructions.

There is another quite different method of transposing a bit matrix: apply three shearing transformations [GLS1]. If the matrix is nxn, the steps are (1) rotate row i to the right i bit positions, (2) rotate column j upwards (j + 1) mod n bit positions, (3) rotate row i to the right (i + 1) mod n bit positions, and (4) reflect the matrix about a horizontal axis through the midpoint. To illustrate, for a 4x4-bit matrix:

This method is not quite competitive with the others because step (2) is costly. (To do it at reasonable cost, rotate upwards all columns that rotate by n/2 or more bit positions by n/2 bit positions [these are columns n/2 - 1 through n - 2], then rotate certain columns upwards n/4 bit positions, and so on.) Steps 1 and 3 require only n - 1 instructions each, and step 4 requires no instructions at all if the results are simply stored to the appropriate locations.

If an 8x8-bit matrix is stored in a 64-bit word in the obvious way (top row in the most significant eight bits, and so on), then the matrix transpose operation is equivalent to three outer perfect shuffles or unshuffles [GLS1]. This is a very good way to do it if your machine has shuffle or unshuffle as a single instruction, but it is not a good method on a basic RISC machine.