8-3 High-Order Product Signed from/to Unsigned

Assume that the machine can readily compute the high-order half of the 64-bit product of two unsigned 32-bit integers, but we wish to perform the corresponding operation on signed integers. We could use the procedure of Figure 8-2, but that requires four multiplications; the procedure to be given [BGN] is much more efficient than that.

The analysis is a special case of that done to convert Knuth's Algorithm M from an unsigned to a signed multiplication routine (Figure 8-1). Let x and y denote the two 32-bit signed integers that we wish to multiply together. The machine will interpret x as an unsigned integer, having the value x + 2³²x₃₁, where x₃₁ is the most significant bit of x (that is, x₃₁ is the integer 1 if x is negative, and 0 otherwise). Similarly, y under unsigned interpretation has the value y + 2³²y₃₁.

Although the result we want is the high-order 32 bits of xy, the machine computes

To get the desired result, we must subtract from this the quantity 2³²(x₃₁y + y₃₁x) + 2⁶⁴x₃₁y₃₁. Because we know that the result can be expressed in 64 bits, we can perform the arithmetic modulo 2⁶⁴. This means that we can safely ignore the last term, and compute the signed high-order product as shown below (seven basic RISC instructions).

Equation 1

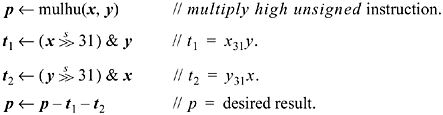
Unsigned from Signed

The reverse transformation follows easily. The resulting program is the same as (1) except with the first instruction changed to multiply high signed and the last operation changed to p p + t₁ + t₂.