9-3 Unsigned Short Division from Signed Division

By "short division" we mean the division of one single word by another (e.g., 32?2 32). It is the form of division provided by the "/" operator, when the operands are integers, in C and many other high-level languages. C has both signed and unsigned short division, but some computers provide only signed division in their instruction repertoire. How can you implement unsigned division on such a machine? There does not seem to be any really slick way to do it, but we offer here some possibilities.

Using Signed Long Division

Even if the machine has signed long division (64?2 32), unsigned short division is not as simple as you might think. In the XLC compiler for the IBM RS/6000, it is implemented as illustrated below for

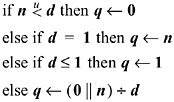
The third line is really testing to see if If d is algebraically less than or equal to 1 at this point, then because it is not equal to 1 (from the second line), it must be algebraically less than or equal to 0. We don't care about the case d = 0, so for the cases of interest, if the test on the third line evaluates to true, the sign bit of d is on, that is, Because from the first line it is known that and because n cannot exceed

The notation on the fourth line means to form the double-length integer consisting of 32 0-bits followed by the 32-bit quantity n, and divide it by d. The test for d = 1 (second line) is necessary to ensure that this division does not overflow (it would overflow if and then the quotient would be undefined).

By commoning the comparisons on the second and third lines, ^[3] the above can be implemented in 11 instructions, three of which are branches. If it is necessary that the divide be executed when d = 0, to get the overflow interrupt, then the third line can be changed to "else if d < 0 then q 1," giving a 12-instruction solution on the RS/6000.

^[3] One execution of the RS/6000's compare instruction sets multiple status bits indicating less than, greater than, or equal.

It is a simple matter to alter the above code so that the probable usual cases do not go through so many tests (begin with d 1 ?, but the code volume increases slightly.

Using Signed Short Division

If signed long division is not available, but signed short division is, then can be implemented by somehow reducing the problem to the case n, d < 2³¹, and using the machine's divide instruction. If then can only be 0 or 1, so this case is easily dispensed with. Then, we can reduce the dividend by using the fact that the expression approximates with an error of only 0 or 1. This leads to the following method:

1.

2.

3.

4.

5.

6.

7.

The test d < 0 on line 1 is really testing to determine if If then the largest the quotient could be is (2³² - 1) ?2³¹ = 1, so the first two lines compute the correct quotient.

Line 4 represents the code shift right unsigned 1, divide, shift left 1. Clearly, and at this point as well, so these quantities can be used in the computer's signed division instruction. (If d = 0, overflow will be signaled here.)

The estimate computed at line 4 is

where we have used the corollary of Theorem D3. Line 5 computes the remainder corresponding to the estimated quotient. It is

Thus, 0 r < 2d. If r < d, then q is the correct quotient. If r d, then adding 1 to q gives the correct quotient (the program must use an unsigned comparison here because of the possibility that r 2³¹).

By moving the load immediate of 0 into q ahead of the comparison and coding the assignment q 1 in line 2 as a branch to the assignment q q + 1 in line 6, this can be coded in 14 instructions on most machines, four of which are branches. It is straightforward to augment the code to produce the remainder as well: to line 1 append r n, to line 2 append r n - d, and to the "then" clause in line 6 append r r - d. (Or, at the cost of a multiply, simply append r n - qd to the end of the whole sequence.)

An alternative for lines 1 and 2 is

which can be coded a little more compactly, for a total of 13 instructions, three of which are branches. But it executes more instructions in what is probably the usual case (small numbers with n > d).

Using predicate expressions, the program can be written

1.

2.

3.

4.

5.

6.

which saves two branches if there is a way to evaluate the predicates without branching. On the Compaq Alpha they can be evaluated in one instruction (CMPULE); on MIPS they take two (SLTU, XORI). On most computers, they can be evaluated in four instructions each (three if equipped with a full set of logic instructions), by using the expression for given in "Comparison Predicates" on page 21, and simplifying because on line 1 of the program above it is known that d₃₁ = 1, and on line 5 it is known that d₃₁ = 0. The expression simplifies to

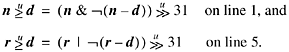
We can get branch-free code by forcing the dividend to be 0 when Then, the divisor can be used in the machine's signed divide instruction, because when it is misinterpreted as a negative number, the result is set to 0, which is within 1 of being correct. We'll still handle the case of a large dividend by shifting it one position to the right before the division, and then shifting the quotient one position to the left after the division. This gives the following program (ten basic RISC instructions):

1.

2.

3.

4.

5.