9-4 Unsigned Long Division
By "long division" we mean the
division of a doubleword by a single word. For a 32-bit machine, this is ![]() division, with the result unspecified in the overflow
cases, including division by 0.
division, with the result unspecified in the overflow
cases, including division by 0.
Some 32-bit machines provide an instruction
for unsigned long division. Its full capability, however, gets little use,
because only ![]() division is accessible
with most high-level languages. Therefore, a computer designer might elect to
provide only
division is accessible
with most high-level languages. Therefore, a computer designer might elect to
provide only ![]() division, and would
probably want an estimate of the execution time of a subroutine that implements
the missing function. Here we give two algorithms for providing this
missing function.
division, and would
probably want an estimate of the execution time of a subroutine that implements
the missing function. Here we give two algorithms for providing this
missing function.
Hardware Shift-and-Subtract Algorithms
As a first attempt at doing long division, we consider doing what the hardware does. There are two algorithms commonly used, called restoring and nonrestoring division [H&P, sec. A-2; EL]. They are both basically "shift-and-subtract" algorithms. In the restoring version, shown below, the restoring step consists of adding back the divisor when the subtraction gives a negative result. Here x, y, and z are held in 32-bit registers. Initially, the double-length dividend is x || y, and the divisor is z. We need a single-bit register c to hold the overflow from the subtraction.
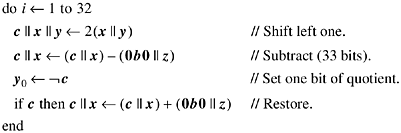
Upon completion, the quotient is in register y and the remainder is in register x.
The algorithm does not give a
useful result in the overflow cases. For division of the doubleword quantity x || y by
0, the quotient obtained is the one's-complement of x, and the remainder obtained is y. In particular, ![]() rem 0. The
other overflow cases are difficult to characterize.
rem 0. The
other overflow cases are difficult to characterize.
It might be useful if, for nonzero divisors, the algorithm
would give the correct quotient modulo 232, and the correct
remainder. However, the only way to do this seems to be to make the register
represented by c || x || y
above 97 bits long, and do the loop 64 times. This is doing ![]() division.
The subtractions would still be 33-bit operations, but the additional hardware
and execution time make this refinement probably not worthwhile.
division.
The subtractions would still be 33-bit operations, but the additional hardware
and execution time make this refinement probably not worthwhile.
This algorithm is difficult to implement exactly in software, because most machines do not have the 33-bit register that we have represented by c || x. Figure 9-2, however, illustrates a shift-and-subtract algorithm that reflects the hardware algorithm to some extent.
The variable t is used for a device to make the comparison come out right. We want to do a 33-bit comparison after shifting x || y. If the first bit of x is 1 (before the shift), then certainly the 33-bit quantity is greater than the divisor (32 bits). In this case, x | t is all 1's, so the comparison gives the correct result (true). On the other hand, if the first bit of x is 0, then a 32-bit comparison is sufficient.
The code of the algorithm in Figure 9-2 executes in 321 to 385 basic RISC instructions, depending upon how often the comparison is true. If the machine has shift left double, the shifting operation can be done in one instruction, rather than the four used above. This would reduce the execution time to about 225 to 289 instructions (we are allowing two instructions per iteration for loop control).
Figure 9-2 Divide long unsigned, shift-and-subtract algorithm.
unsigned divlu(unsigned x, unsigned y, unsigned z) {牋 // Divides (x || y) by z.
牋爄nt i;
牋爑nsigned t;
牋 for (i = 1; i <= 32; i++) {牋牋?t = (int)x >> 31;牋牋牋牋 // All 1's if x(31) = 1.
牋牋牋x = (x << 1) | (y >> 31); // Shift x || y left
牋牋牋y = y << 1;牋牋牋牋牋牋牋 // one bit.
牋牋牋if ((x | t) >= z) {牋牋牋牋 x = x - z;
牋牋牋牋爕 = y + 1;
牋牋牋}
牋爙
牋爎eturn y;牋牋牋牋牋牋牋牋牋?// Remainder is x.
}
The algorithm in Figure 9-2 can be used to do ![]() division
by supplying x = 0. The only
simplification that results is that the variable t can be omitted, as its value would always be 0.
division
by supplying x = 0. The only
simplification that results is that the variable t can be omitted, as its value would always be 0.
Below is the nonrestoring hardware division algorithm (unsigned). The basic idea is that, after subtracting the divisor z from the 33-bit quantity that we denote by c || x, there is no need to add back z if the result was negative. Instead, it suffices to add on the next iteration, rather than subtract. This is because adding z (to correct the error of having subtracted z on the previous iteration), shifting left, and subtracting z is equivalent to adding z (2(u + z) - z = 2u + z). The advantage to hardware is that there is only one add or subtract operation on each loop iteration, and the adder is likely to be the slowest circuit in the loop. [4] An adjustment to the remainder is needed at the end, if it is negative. (No corresponding adjustment of the quotient is required.)
[4] Actually, the restoring division algorithm can avoid the restoring step by putting the result of the subtraction in an additional register, and writing that register into x only if the result of the subtraction (33 bits) is nonnegative. But in some implementations this may require an additional register and possibly more time.
The input dividend is the doubleword quantity x || y, and the divisor is z. Upon completion, the quotient is in register y and the remainder is in register x.

This does not seem to adapt very well to a 32-bit algorithm.
The 801 minicomputer (an early experimental RISC machine built by IBM) had a divide step instruction that essentially performed the steps in the body of the loop above. It used the machine's carry status bit to hold c, and the MQ (a 32-bit register) to hold y. A 33-bit adder/subtracter is needed for its implementation. The 801's divide step instruction was a little more complicated than the loop above, because it performed signed division and it had an overflow check. Using it, a division subroutine can be written that consists essentially of 32 consecutive divide step instructions followed by some adjustments to the quotient and remainder to make the remainder have the desired sign.
Using Short Division
An algorithm for ![]() division can be
obtained from the multiword division algorithm of Figure 9-1 on page 141, by specializing it to
the case m = 4, n
= 2. Several other changes are necessary. The parameters should be fullwords
passed by value, rather than arrays of halfwords. The overflow condition is
different; it occurs if the quotient cannot be contained in a single fullword.
It turns out that many simplifications to the routine are possible. It can be
shown that the guess qhat is
always exact; it is exact if the divisor consists of only two halfword digits.
This means that the "add back" steps can be omitted. If the
"main loop" of Figure 9-1 and the loop within it are
unrolled, some minor simplifications become possible.
division can be
obtained from the multiword division algorithm of Figure 9-1 on page 141, by specializing it to
the case m = 4, n
= 2. Several other changes are necessary. The parameters should be fullwords
passed by value, rather than arrays of halfwords. The overflow condition is
different; it occurs if the quotient cannot be contained in a single fullword.
It turns out that many simplifications to the routine are possible. It can be
shown that the guess qhat is
always exact; it is exact if the divisor consists of only two halfword digits.
This means that the "add back" steps can be omitted. If the
"main loop" of Figure 9-1 and the loop within it are
unrolled, some minor simplifications become possible.
The result of these transformations is shown in Figure 9-3. The dividend is in u1 and u0, with u1 containing the most significant word. The divisor is parameter v. The quotient is the returned value of the function. If the caller provides a non-null pointer in parameter r, the function will return the remainder in the word to which r points.
For an overflow indication, the program returns a remainder equal to the maximum unsigned integer. This is an impossible remainder for a valid division operation, because the remainder must be less than the divisor. In the overflow case, the program also returns a quotient equal to the maximum unsigned integer, which may be an adequate indicator in some cases in which the remainder is not wanted.
The strange expression (-s >> 31) in the assignment to u32 is supplied to make the program work for the case s = 0 on machines that have mod 32 shifts (e.g., Intel x86).
Experimentation with uniformly distributed random numbers suggests that the bodies of the "again" loops are each executed about 0.38 times for each execution of the function. This gives an execution time, if the remainder is not wanted, of about 52 instructions. Of these instructions, one is number of leading zeros, two are divide, and 6.5 are multiply (not counting the multiplications by b, which are shift's). If the remainder is wanted, add six instructions (counting the store of r), one of which is multiply.
What about a signed version of divlu? It would probably be difficult to modify the code of Figure 9-3, step by step, to produce a signed variant. That algorithm, however, may be used for signed division by taking the absolute value of the arguments, running divlu, and then complementing the result if the signs of the original arguments differ. There is no problem with extreme values such as the maximum negative number, because the absolute value of any signed integer has a correct representation as an unsigned integer. This algorithm is shown in Figure 9-4.
Figure 9-3 Divide long unsigned, using fullword division instruction.
unsigned divlu(unsigned u1, unsigned u0, unsigned v,
牋牋牋牋牋牋牋爑nsigned *r)?{牋 const unsigned b = 65536; // Number base (16 bits).
牋爑nsigned un1, un0,牋牋牋?// Norm. dividend LSD's.
牋牋牋牋牋牋vn1, vn0,牋牋牋?// Norm. divisor digits.
牋牋牋牋牋牋q1, q0,牋牋牋牋?// Quotient digits.
牋牋牋牋牋牋un32, un21, un10,// Dividend digit pairs.
牋牋牋牋牋牋rhat;牋牋牋牋牋?// A remainder.
牋爄nt s;牋牋牋牋牋牋牋牋牋?// Shift amount for norm.
牋 if (u1 >= v) {牋牋牋牋牋?// If overflow, set rem. 牋牋牋if (r != NULL)牋牋牋牋 // to an impossible value,
牋牋牋牋?r = 0xFFFFFFFF;牋?// and return the largest
牋牋牋return 0xFFFFFFFF;}牋?// possible quotient.
牋 s = nlz(v);牋牋牋牋牋牋牋 // 0 <= s <= 31.
牋爒 = v << s;牋牋牋牋牋牋牋 // Normalize divisor.
牋爒n1 = v >> 16;牋牋牋牋牋?// Break divisor up into
牋爒n0 = v & 0xFFFF;牋牋牋牋 // two 16-bit digits.
牋 un32 = (u1 << s) | (u0 >> 32 - s) & (-s >> 31);
牋爑n10 = u0 << s;牋牋牋牋牋 // Shift dividend left.
牋 un1 = un10 >> 16;牋牋牋牋 // Break right half of
牋爑n0 = un10 & 0xFFFF;牋 牋?/ dividend into two digits.
牋 q1 = un32/vn1;牋牋牋牋牋?// Compute the first
牋爎hat = un32 - q1*vn1;牋牋 // quotient digit, q1.
again1:
牋爄f (q1 >= b || q1*vn0 > b*rhat + un1) {牋牋 q1 = q1 - 1;
牋牋爎hat = rhat + vn1;
牋牋爄f (rhat < b) goto again1;}
牋 un21 = un32*b + un1 - q1*v;?// Multiply and subtract.
牋 q0 = un21/vn1;牋牋牋牋牋?// Compute the second
牋爎hat = un21 - q0*vn1;牋牋 // quotient digit, q0.
again2:
牋爄f (q0 >= b || q0*vn0 > b*rhat + un0) {牋牋 q0 = q0 - 1;
牋牋爎hat = rhat + vn1;
牋牋爄f (rhat < b) goto again2;}
牋 if (r != NULL)牋牋牋牋牋?// If remainder is wanted,
牋牋牋*r = (un21*b + un0 - q0*v) >> s;牋牋 // return it.
牋爎eturn q1*b + q0;
}
Figure 9-4 Divide long signed, using divide long unsigned.
int divls(int u1, unsigned u0, int v, int *r) {牋 int q, uneg, vneg, diff, borrow; 牋 uneg = u1 >> 31;牋牋牋牋?// -1 if u < 0. 牋爄f (uneg) {牋牋牋牋牋牋牋 // Compute the absolute 牋牋牋u0 = -u0;牋牋牋牋牋牋?// value of the dividend u. 牋牋牋borrow = (u0 != 0); 牋牋牋u1 = -u1 - borrow;} 牋 vneg = v >> 31;牋牋牋牋牋 // -1 if v < 0. 牋爒 = (v ^ vneg) - vneg;牋?// Absolute value of v. 牋 if ((unsigned)u1 >= (unsigned)v) goto overflow; 牋 q = divlu(u1, u0, v, (unsigned *)r); 牋 diff = uneg ^ vneg;牋牋牋 // Negate q if signs of 牋爍 = (q ^ diff) - diff;牋?// u and v differed. 牋爄f (uneg && r != NULL) 牋牋牋*r = -*r; 牋 if ((diff ^ q) < 0 && q != 0) {?// If overflow, overflow:牋牋牋牋牋牋牋牋牋?// set remainder 牋牋牋if (r != NULL)牋 牋牋牋// to an impossible value, 牋牋牋牋?r = 0x80000000;牋?// and return the largest 牋牋牋q = 0x80000000;}牋牋牋 // possible neg. quotient. 牋爎eturn q; }
It is hard to devise really good code to detect overflow in the signed case. The algorithm shown in Figure 9-4 makes a preliminary determination identical to that used by the unsigned long division routine, which ensures that |u/v| <232. After that, it is necessary only to ensure that the quotient has the proper sign or is 0.