10-3 Signed Division and Remainder by Non-Powers of 2

The basic trick is to multiply by a sort of reciprocal of the divisor d, approximately 2³²/d, and then to extract the leftmost 32 bits of the product. The details, however, are more complicated, particularly for certain divisors such as 7.

Let us first consider a few specific examples. These illustrate the code that will be generated by the general method. We denote registers as follows:

n - the input integer (numerator)

M - loaded with a "magic number"

t - a temporary register

q - will contain the quotient

r - will contain the remainder

Divide by 3

li  ?M,0x55555556?Load magic number, (2**32+2)/3. 
mulhs q,M,n         q = floor(M*n/2**32). 
shri?t,n,31      ?Add 1 to q if 
add   q,q,t         n is negative. 
 
muli?t,q,3         Compute remainder from 
sub   r,n,t         r = n - q*3. 

Proof. The multiply high signed operation (mulhs) cannot overflow, as the product of two 32-bit integers can always be represented in 64 bits and mulhs gives the high-order 32 bits of the 64-bit product. This is equivalent to dividing the 64-bit product by 2³² and taking the floor of the result, and this is true whether the product is positive or negative. Thus, for n 0 the above code computes

Now, n < 2³¹, because 2³¹ - 1 is the largest representable positive number. Hence the "error" term 2n/(3 ?2³²) is less than 1/3 (and is nonnegative), so by Theorem D4 (page 139) we have which is the desired result (Equation (1) on page 138).

For n < 0, there is an addition of 1 to the quotient. Hence the code computes

where we have used Theorem D2. Hence

For -2³¹ n - 1,

The error term is nonpositive and greater than -1/3, so by Theorem D4 which is the desired result (Equation (1) on page 138).

This establishes that the quotient is correct. That the remainder is correct follows easily from the fact that the remainder must satisfy

the multiplication by 3 cannot overflow (because -2³¹/3 q (2³¹ - 1)/3), and the subtract cannot overflow because the result must be in the range -2 to +2.

The multiply immediate can be done with two add's, or a shift and an add, if either gives an improvement in execution time.

On many present-day RISC computers, the quotient can be computed as shown above in nine or ten cycles, whereas the divide instruction might take 20 cycles or so.

Divide by 5

For division by 5, we would like to use the same code as for division by 3, except with a multiplier of (2³² + 4)/5. Unfortunately, the error term is then too large; the result is off by 1 for about 1/5 of the values of n 2³⁰ in magnitude. However, we can use a multiplier of (2³³ + 3)/5 and add a shift right signed instruction. The code is

li  ?M,0x66666667?Load magic number, (2**33+3)/5. 
mulhs q,M,n         q = floor(M*n/2**32). 
shrsi q,q,1 
shri?t,n,31      ?Add 1 to q if 
add   q,q,t         n is negative. 
 
muli?t,q,5         Compute remainder from 
sub   r,n,t         r = n - q*5. 

Proof. The mulhs produces the leftmost 32 bits of the 64-bit product, and then the code shifts this right by one position, signed (or "arithmetically"). This is equivalent to dividing the product by 2³³ and then taking the floor of the result. Thus, for n 0 the code computes

For 0 n < 2³¹, the error term 3n/5 ?2³³ is nonnegative and less than 1/5, so by Theorem D4,

For n < 0 the above code computes

The error term is nonpositive and greater than -1/5, so

That the remainder is correct follows as in the case of division by 3.

The multiply immediate can be done with a shift left of two and an add.

Divide by 7

Dividing by 7 creates a new problem. Multipliers of (2³² + 3)/7 and (2³³ + 6)/7 give error terms that are too large. A multiplier of (2³⁴ + 5)/7 would work, but it's too large to represent in a 32-bit signed word. We can multiply by this large number by multiplying by (2³⁴ + 5)/7 - 2³² (a negative number), and then correcting the product by inserting an add. The code is

li  ?M,0x92492493?Magic num, (2**34+5)/7 - 2**32. 
mulhs q,M,n         q = floor(M*n/2**32). 
add   q,q,n         q = floor(M*n/2**32) + n. 
shrsi q,q,2         q = floor(q/4). 
shri?t,n,31      ?Add 1 to q if 
add   q,q,t         n is negative. 
 
muli?t,q,7         Compute remainder from 
sub   r,n,t         r = n - q*7. 

Proof. It is important to note that the instruction "add q,q,n" above cannot overflow. This is because q and n have opposite signs, due to the multiplication by a negative number. Therefore, this "computer arithmetic" addition is the same as real number addition. Hence for n 0 the above code computes

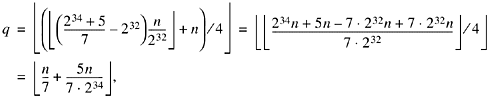
where we have used the corollary of Theorem D3.

For 0 n < 2³¹, the error term 5n/7 ?2³⁴ is nonnegative and less than 1/7, so

For n < 0, the above code computes

The error term is nonpositive and greater than -1/7, so

The multiply immediate can be done with a shift left of three and a subtract.