10-5 Signed
Division by Divisors  -2
-2
Because signed integer division satisfies n ?(-d) = -(n ?d) it is adequate to generate code for n ?|d| and follow it with an instruction to negate the quotient. (This does not give the correct result for d = -2W - 1, but for this and other negative powers of 2, you can use the code in Section 10-1, "Signed Division by a Known Power of 2," on page 155, followed by a negating instruction.) It will not do to negate the dividend, because of the possibility that it is the maximum negative number.
It is possible, however, to avoid the negating instruction. The scheme is to compute
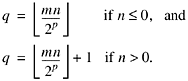
Adding 1 if n > 0, however, is awkward (because one cannot simply use the sign bit of n), so the code will instead add 1 if q < 0. This is equivalent because the multiplier m is negative (as will be seen).
The code to be generated is illustrated below for the case W = 32, d = -7.
li 牋燤,0x6DB6DB6D?Magic num, -(2**34+5)/7 + 2**32. mulhs q,M,n牋牋牋牋 q = floor(M*n/2**32). sub牋 q,q,n牋牋牋牋 q = floor(M*n/2**32) - n. shrsi q,q,2牋牋牋牋 q = floor(q/4). shri?t,q,31牋牋牋?Add 1 to q if add牋 q,q,t牋牋牋牋 q is negative (n is positive). muli?t,q,-7牋牋牋?Compute remainder from sub牋 r,n,t牋牋牋牋 r = n - q*(-7).
This code is the same as that for division by +7, except that it uses the negative of the multiplier for +7, and a sub rather than an add after the multiply, and the shri of 31 must use q rather than n, as discussed above. (The case of d = +7 could also use q here, but there would be less parallelism in the code.) The subtract will not overflow because the operands have the same sign. This scheme, however, does not always work! Although the code above for W = 32, d = -7 is correct, the analogous alteration of the "divide by 3" code to produce code to divide by -3 does not give the correct result for W = 32, n = -231.
Let us look at the situation more closely.
Given a word size W
![]() 3 and a divisor d, -2W - 1
3 and a divisor d, -2W - 1 ![]() d
d ![]() -2, we wish to find the
least (in absolute value) integer m and integer
p such that
-2, we wish to find the
least (in absolute value) integer m and integer
p such that
![]()
![]()
with -2W
![]() m
m ![]() 0 and
p
0 and
p ![]() W.
W.
Proceeding similarly to the case of division
by a positive divisor, let nc be the
most negative value of n such that nc = kd +
1 for some integer k. nc
exists because one possibility is nc
= d + 1. It can be calculated from ![]() nc is one of the least |d| admissible
values of n, so
nc is one of the least |d| admissible
values of n, so
![]()
and clearly
![]()
Because (14b) must hold for n = -d, and (14a) must hold for n = nc, we obtain, analogous to (4),
![]()
Because m is to be the greatest integer satisfying (16), it is the next integer less than 2p/d梩hat is,
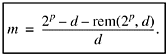
Combining this with the left half of (16) and simplifying gives
![]()
The proof that the algorithm suggested by
(17) and (18) is feasible and that the product is correct is similar to that
for a positive divisor, and will not be repeated. A difficulty arises, however,
in trying to prove that -2W ![]() m
m ![]() 0. To
prove this, consider separately the cases in which d
is the negative of a power of 2, or some other number. For d = -2k it
is easy to show that nc = - 2W - 1 + 1, p = W + k - 1, and m = - 2W - 1 - 1 (which is within
range). For d not of the form -2k, it is straightforward to alter the
earlier proof.
0. To
prove this, consider separately the cases in which d
is the negative of a power of 2, or some other number. For d = -2k it
is easy to show that nc = - 2W - 1 + 1, p = W + k - 1, and m = - 2W - 1 - 1 (which is within
range). For d not of the form -2k, it is straightforward to alter the
earlier proof.
For Which Divisors Is m(-d)  -m(d)?
-m(d)?
By m(d) we mean the multiplier corresponding to a divisor d. If m(-d) = -m(d), code for division by a negative divisor can be generated by calculating the multiplier for |d|, negating it, and then generating code similar to that of the "divide by 7" case illustrated above.
By comparing (18) with (6) and (17) with (5),
it can be seen that if the value of nc
for -d is the negative of that for d, then m(-d) = -m(d). Hence m(-d) ![]() m(d) can occur only when the value of
nc calculated for the negative
divisor is the maximum negative number, -2W
- 1. Such divisors are the negatives of the factors of 2W - 1 + 1. These numbers are
fairly rare, as illustrated by the factorings below (obtained from Scratchpad).
m(d) can occur only when the value of
nc calculated for the negative
divisor is the maximum negative number, -2W
- 1. Such divisors are the negatives of the factors of 2W - 1 + 1. These numbers are
fairly rare, as illustrated by the factorings below (obtained from Scratchpad).

For all these
factors, m(-d) ![]() m(d). Proof sketch: For d
> 0 we have nc = 2W - 1 - d. Because rem(2W - 1,
d) = d - 1, (6)
is satisfied by p = W
- 1 and hence also by p = W. For d < 0,
however, we have nc = -2W - 1 and rem(2W - 1, d) = |d| - 1. Hence
(18) is not satisfied for p = W - 1 or for p = W, so p > W.
m(d). Proof sketch: For d
> 0 we have nc = 2W - 1 - d. Because rem(2W - 1,
d) = d - 1, (6)
is satisfied by p = W
- 1 and hence also by p = W. For d < 0,
however, we have nc = -2W - 1 and rem(2W - 1, d) = |d| - 1. Hence
(18) is not satisfied for p = W - 1 or for p = W, so p > W.