10-6 Incorporation into a Compiler

For a compiler to change division by a constant into a multiplication, it must compute the magic number M and the shift amount s, given a divisor d. The straightforward computation is to evaluate (6) or (18) for p = W, W + 1, ?until it is satisfied. Then, m is calculated from (5) or (17). M is simply a reinterpretation of m as a signed integer, and s = p - W.

The scheme described below handles positive and negative d with only a little extra code, and it avoids doubleword arithmetic.

Recall that n_c is given by

Hence |n_c| can be computed from

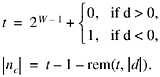
The remainder must be evaluated using unsigned division, because of the magnitude of the arguments. We have written rem(t, |d|) rather than the equivalent rem(t, d), to emphasize that the program must deal with two positive (and unsigned) arguments.

From (6) and (18), p can be calculated from

Equation 19

and then |m| can be calculated from (c.f. (5) and (17)):

Equation 20

Direct evaluation of rem(2^p,|d|) in (19) requires "long division" (dividing a 2W-bit dividend by a W-bit divisor, giving a W-bit quotient and remainder), and in fact it must be unsigned long division. There is a way to solve (19), and in fact to do all the calculations, that avoids long division and can easily be implemented in a conventional HLL using only W-bit arithmetic. We do, however, need unsigned division and unsigned comparisons.

We can calculate rem(2^p, |d|) incrementally, by initializing two variables q and r to the quotient and remainder of 2^p divided by |d| with p = 2^{W - 1}, and then updating q and r as p increases.

As the search progresses—that is, when p is incremented by 1?span class=docemphasis1>q and r are updated from (see Theorem D5(a))

q = 2*q; 
r = 2*r; 
if (r >= abs(d)) {
   q = q + 1; 
   r = r - abs(d);} 

The left half of inequality (4) and the right half of (16), together with the bounds proved for m, imply that so q is representable as a W-bit unsigned integer. Also, 0 r < |d| so r is representable as a W-bit signed or unsigned integer. (Caution: The intermediate result 2r can exceed 2^{W - 1} - 1, so r should be unsigned and the comparison above should also be unsigned.)

Next, calculate d = |d| - r. Both terms of the subtraction are representable as W-bit unsigned integers, and the result is also (1 d |d|), so there is no difficulty here.

To avoid the long multiplication of (19), rewrite it as

The quantity is representable as a W-bit unsigned integer (similarly to (7), from (19) it can be shown that and, for d = -2^{W - 1}, n_c = - 2^{W - 1} + 1 and p = 2W - 2 so that for W 3). Also, it is easily calculated incrementally (as p increases) in the same manner as for rem(2^p, |d|). The comparison should be unsigned, for the case (which can occur, for large d).

To compute m, we need not evaluate (20) directly (which would require long division). Observe that

The loop closure test is awkward to evaluate. The quantity is available only in the form of a quotient q₁ and a remainder may or may not be an integer (it is an integer only for d = 2^{W - 2} + 1 and a few negative values of d). The test may be coded as

The complete procedure for computing M and s from d is shown in Figure 10-1, coded in C, for W = 32. There are a few places where overflow can occur, but the correct result is obtained if overflow is ignored.

Figure 10-1 Computing the magic number for signed division.

struct ms {int M;        ?// Magic number 
          int s;};         // and shift amount. 
 
struct ms magic(int d) {   // Must have 2 <= d <= 2**31-1 
                          ?/ or   -2**31 <= d <= -2. 
   int p; 
   unsigned ad, anc, delta, q1, r1, q2, r2, t; 
   const unsigned two31 = 0x80000000;     // 2**31. 
   struct ms mag; 
 
   ad = abs(d); 
   t = two31 + ((unsigned)d >> 31); 
   anc = t - 1 - t%ad;     // Absolute value of nc. 
   p = 31;                 // Init. p. 
   q1 = two31/anc;         // Init. q1 = 2**p/|nc|. 
   r1 = two31 - q1*anc;  ?// Init. r1 = rem(2**p, |nc|). 
   q2 = two31/ad;        ?// Init. q2 = 2**p/|d|. 
   r2 = two31 - q2*ad;     // Init. r2 = rem(2**p, |d|). 
   do {
    ?p = p + 1; 
      q1 = 2*q1;           // Update q1 = 2**p/|nc|. 
 r1 = 2*r1;           // Update r1 = rem(2**p, |nc|. 
 if (r1 >= anc) {     // (Must be an unsigned 
         q1 = q1 + 1;    ?// comparison here). 
         r1 = r1 - anc;} 
      q2 = 2*q2;           // Update q2 = 2**p/|d|. 
 r2 = 2*r2;           // Update r2 = rem(2**p, |d|. 
 if (r2 >= ad) {    ?// (Must be an unsigned 
         q2 = q2 + 1;    ?// comparison here). 
         r2 = r2 - ad;} 
 delta = ad - r2; 
   } while (q1 < delta || (q1 == delta && r1 == 0)); 
 
 mag.M = q2 + 1; 
   if (d < 0) mag.M = -mag.M; // Magic number and 
   mag.s = p - 32;          ?// shift amount to return. 
   return mag; 
} 

To use the results of this program, the compiler should generate the li and mulhs instructions, generate the add if d > 0 and M < 0, or the sub if d < 0 and M > 0, and generate the shrsi if s > 0. Then, the shri and final add must be generated.

For W = 32, handling a negative divisor may be avoided by simply returning a precomputed result for d = 3 and d = 715,827,883, and using m(-d) = -m(d) for other negative divisors. However, that program would not be significantly shorter, if at all, than the one given in Figure 10-1.