10-8 Unsigned Division

Unsigned division by a power of 2 is of course implemented by a single shift right logical instruction, and remainder by and immediate.

It might seem that handling other divisors will be simple: Just use the results for signed division with d > 0, omitting the two instructions that add 1 if the quotient is negative. We will see, however, that some of the details are actually more complicated in the case of unsigned division.

Unsigned Divide by 3

For a non-power of 2, let us first consider unsigned division by 3 on a 32-bit machine. Because the dividend n can now be as large as 2³² - 1, the multiplier (2³² + 2)/3 is inadequate, because the error term 2n/3 ?2³² (see "divide by 3" example above) can exceed 1/3. However, the multiplier (2³³ + 1)/3 is adequate. The code is

li  ?M,0xAAAAAAAB?Load magic number, (2**33+1)/3. 
mulhu q,M,n         q = floor(M*n/2**32). 
shri?q,q,1 
 
muli?t,q,3         Compute remainder from 
sub   r,n,t         r = n - q*3. 

An instruction that gives the high-order 32 bits of a 64-bit unsigned product is required, which we show above as mulhu.

To see that the code is correct, observe that it computes

For 0 n < 2³², 0 n/(3 ?2³³) < 1/3, so by Theorem D4,

In computing the remainder, the multiply immediate can overflow if we regard the operands as signed integers, but it does not overflow if we regard them and the result as unsigned. Also, the subtract cannot overflow, because the result is in the range 0 to 2, so the remainder is correct.

Unsigned Divide by 7

For unsigned division by 7 on a 32-bit machine, the multipliers (2³² + 3)/7, (2³³ + 6)/7, and (2³⁴ + 5)/7 are all inadequate because they give too large an error term. The multiplier (2³⁵ + 3)/7 is acceptable, but it's too large to represent in a 32-bit unsigned word. We can multiply by this large number by multiplying by (2³⁵ + 3)/7 - 2³² and then correcting the product by inserting an add. The code is

li  ?M,0x24924925?Magic num, (2**35+3)/7 - 2**32. 
mulhu q,M,n         q = floor(M*n/2**32). 
add   q,q,n         Can overflow (sets carry). 
shrxi q,q,3         Shift right with carry bit. 
 
muli?t,q,7         Compute remainder from 
sub   r,n,t         r = n - q*7. 

Here we have a problem: The add can overflow. To allow for this, we have invented the new instruction shift right extended immediate (shrxi), which treats the carry from the add and the 32 bits of register q as a single 33-bit quantity, and shifts it right with 0-fill. On the Motorola 68000 family, this can be done with two instructions: rotate with extend right one position, followed by a logical right shift of three (roxr actually uses the X bit, but the add sets the X bit the same as the carry bit). On most machines, it will take more. For example, on PowerPC it takes three instructions: clear rightmost three bits of q, add carry to q, and rotate right three positions.

With shrxi implemented somehow, the code above computes

For 0 n < 2³², 0 3n/(7 ?2³⁵) < 1/7, so by Theorem D4,

Granlund and Montgomery [GM] have a clever scheme for avoiding the shrxi instruction. It requires the same number of instructions as the above three-instruction sequence for shrxi, but it employs only elementary instructions that almost any machine would have, and it does not cause overflow at all. It uses the identity

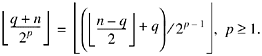
Applying this to our problem, with where 0 M < 2³², the subtraction will not overflow because

so that clearly 0 n - q < 2³². Also, the addition will not overflow, because

and 0 n, q < 2³².

Using this idea gives the following code for unsigned division by 7:

li  ?M,0x24924925?Magic num, (2**35+3)/7 - 2**32. 
mulhu q,M,n         q = floor(M*n/2**32). 
sub   t,n,q         t = n - q. 
shri?t,t,1         t = (n - q)/2. 
add   t,t,q         t = (n - q)/2 + q = (n + q)/2. 
shri?q,t,2         q = (n+Mn/2**32)/8 = floor(n/7). 
 
muli?t,q,7         Compute remainder from 
sub   r,n,t         r = n - q*7. 

For this to work, the shift amount for the hypothetical shrxi instruction must be greater than 0. It can be shown that if d > 1 and the multiplier m 2³² (so that the shrxi instruction is needed), then the shift amount is greater than 0.