10-15 Exact Division by Constants

By "exact division," we mean division in which it is known beforehand, somehow, that the remainder is 0. Although this situation is not common, it does arise, for example, when subtracting two pointers in the C language. In C, the result of p - q, where p and q are pointers, is well defined and portable only if p and q point to objects in the same array [H&S, sec. 7.6.2]. If the array element size is s, the object code for the difference p - q computes (p - q)/s.

The material in this section was motivated by [GM, sec. 9].

The method to be given applies to both signed and unsigned exact division, and is based on the following theorem.

Theorem MI. If a and m are relatively prime integers, then there exists an integer a? 1 a?/span> < m, such that

Thus a?/span> is a multiplicative inverse of a, modulo m. There are several ways to prove this theorem; three proofs are given in [NZM, 52]. The proof below requires only a very basic familiarity with congruences.

Proof. We will prove something a little more general than the theorem. If a and m are relatively prime (and hence nonzero), then as x ranges over all m distinct values modulo m, ax takes on all m distinct values modulo m. For example, if a = 3 and m = 8, then as x ranges from 0 to 7, ax = 0, 3, 6, 9, 12, 15, 18, 21 or, reduced modulo 8, ax = 0, 3, 6, 1, 4, 7, 2, 5. Observe that all values from 0 to 7 are present in the last sequence.

To see this in general, assume that it is not true. Then there exist distinct integers that map to the same value when multiplied by a; that is, there exist x and y, with x y (mod m), such that

But then there exists an integer k such that

Because a has no factor in common with m, it must be that x - y is a multiple of m; that is,

This contradicts the hypothesis.

Now, because ax takes on all m distinct values modulo m, as x ranges over the m values, it must take on the value 1 for some x.

The proof shows that there is only one value (modulo m) of x such that ax 1 (mod m)—that is, the multiplicative inverse is unique, apart from additive multiples of m. It also shows that there is a unique (modulo m) integer x such that ax b (mod m)where b is any integer.

As an example, consider the case m = 16. Then because 3?1 = 33 1 (mod 16). We could just as well take because 3?-5) = -15 1 (mod 16). Similarly, because (-3)? = -15 1 (mod 16).

These observations are important because they show that the concepts apply to both signed and unsigned numbers. If we are working in the domain of unsigned integers on a 4-bit machine, we take In the domain of signed integers, we take But 11 and -5 have the same representation in two's-complement (because they differ by 16), so the same computer word contents can serve in both domains as the multiplicative inverse.

The theorem applies directly to the problem of division (signed and unsigned) by an odd integer d on a W-bit computer. Because any odd integer is relatively prime to 2^W, the theorem says that if d is odd, there exists an integer d?/span> (unique in the range 0 to 2^W - 1 or in the range -2^{W - 1} to 2^{W - 1} - 1) such that

Hence for any integer n that is a multiple of d,

In other words, n/d can be calculated by multiplying n by d?/span>, and retaining only the rightmost W bits of the product.

If the divisor d is even, let d = d_o ?2^k, where d_o is odd and k 1. Then, simply shift n right k positions (shifting out 0's), and then multiply by (the shift could be done after the multiplication as well).

Below is the code for division of n by 7, where n is a multiple of 7. This code gives the correct result whether it is considered to be signed or unsigned division.

li  ?M,0xB6DB6DB7?Mult. inverse, (5*2**32 + 1)/7. 
mul   q,M,n         q = n/7. 

Computing the Multiplicative Inverse by the Euclidean Algorithm

How can we compute the multiplicative inverse? The standard method is by means of the "extended Euclidean algorithm." This is briefly discussed below as it applies to our problem, and the interested reader is referred to [NZM, 13] and to [Knu2, sec. 4.5.2] for a more complete discussion.

Given an odd divisor d, we wish to solve for x

where, in our application, m = 2^W and W is the word size of the machine. This will be accomplished if we can solve for integers x and y (positive, negative, or 0) the equation

Toward this end, first make d positive by adding a sufficient number of multiples of m to it. (d and d + km have the same multiplicative inverse.) Second, write the following equations (in which d, m > 0):

If d = 1, we are done, because (ii) shows that x = 1. Otherwise, compute

Third, multiply Equation (ii) by q and subtract it from (i). This gives

This equation holds because we have simply multiplied one equation by a constant and subtracted it from another. If rem(m - d, d) = 1, we are done; this last equation is the solution and x = - 1 - q.

Repeat this process on the last two equations, obtaining a fourth, and continue until the right-hand side of the equation is 1. The multiplier of d, reduced modulo m, is then the desired inverse of d.

Incidentally, if m - d < d, so that the first quotient is 0, then the third row will be a copy of the first, so that the second quotient will be nonzero. Furthermore, most texts start with the first row being

but in our application m = 2^W is not representable in the machine.

The process is best illustrated by an example. Let m = 256 and d = 7. Then the calculation proceeds as follows. To get the third row, note that

7(-1) + 256( 1) = 249 
7( 1) + 256( 0) = 7 
7(-36) + 256( 1) = 4 
7( 37) + 256(-1) = 3 
7(-73) + 256( 2) = 1 

Thus, the multiplicative inverse of 7, modulo 256, is -73 or, expressed in the range 0 to 255, is 183. Check: 7?83 = 1281 1 (mod 256).

From the third row on, the integers in the right-hand column are all remainders with respect to the number above it as a divisor (d being the dividend), so they form a sequence of strictly decreasing nonnegative integers. Therefore, the sequence must end in 0 (as the above would if carried one more step). Furthermore, the value just before the 0 must be 1, for the following reason. Suppose the sequence ends in b followed by 0, with b 1. Then, the integer preceding the b must be a multiple of b, let's say k₁b, for the next remainder to be 0. The integer preceding k₁b must be of the form k₁k₂b + b, for the next remainder to be b. Continuing up the sequence, every number must be a multiple of b, including the first two (in the positions of the 249 and the 7 in the above example). But this is impossible, because the first two integers are m - d and d, which are relatively prime.

This constitutes an informal proof that the above process terminates, with a value of 1 in the right-hand column, and hence it finds the multiplicative inverse of d.

To carry this out on a computer, first note that if d < 0 we should add 2^W to it. But with two's-complement arithmetic it is not necessary to actually do anything here; simply interpret d as an unsigned number regardless of how the application interprets it.

The computation of q must use unsigned division.

Observe that the calculations can be done modulo m, because this does not change the right-hand column (these values are in the range 0 to m - 1 anyway). This is important, because it enables the calculations to be done in "single precision," using the computer's modulo-2^W unsigned arithmetic.

Most of the quantities in the table need not be represented. The column of multiples of 256 need not be represented, because in solving dx + my = 1, we do not need the value of y. There is no need to represent d in the first column. Reduced to its bare essentials, then, the calculation of the above example is carried out as follows:

255?249 
  1  ?7 
220  ?4 
?7  ?3 
183  ?1 

A C program for performing this computation is shown in Figure 10-4.

Figure 10-4 Multiplicative inverse modulo 2³² by the Euclidean algorithm.

unsigned mulinv(unsigned d) {           // d must be odd. 
   unsigned x1, v1, x2, v2, x3, v3, q; 
 
   x1 = 0xFFFFFFFF;     v1 = -d; 
   x2 = 1;            ?v2 = d; 
   while (v2 > 1) {
      q = v1/v2; 
      x3 = x1 - q*x2;   v3 = v1 - q*v2; 
      x1 = x2;        ?v1 = v2; 
      x2 = x3;        ?v2 = v3; 
   } 
   return(x2); 
} 

The reason the loop continuation condition is (v2 > 1) rather than the more natural (v2 != 1) is that if the latter condition were used, the loop would never terminate if the program were invoked with an even argument. It is best that programs not loop forever even if misused. (If the argument d is even, v2 never takes on the value 1, but it does become 0.)

What does the program compute if given an even argument? As written, it computes a number x such that dx 0 (mod 2³²), which is probably not useful. However, with the minor modification of changing the loop continuation condition to (v2 != 0) and returning x1 rather than x2, it computes a number x such that dx g (mod 2³²) where g is the greatest common divisor of d and 2³²—that is, the greatest power of 2 that divides d. The modified program still computes the multiplicative inverse of d for d odd, but it requires one more iteration than the unmodified program.

As for the number of iterations (divisions) required by the above program, for d odd and less than 20, it requires a maximum of 3 and an average of 1.7. For d in the neighborhood of 1000, it requires a maximum of 11 and an average of about 6.

Computing the Multiplicative Inverse by Newton's Method

It is well known that, over the real numbers, 1/d, for d 0, can be calculated to ever increasing accuracy by iteratively evaluating

Equation 31

provided the initial estimate x₀ is sufficiently close to 1/d. The number of digits of accuracy approximately doubles with each iteration.

It is not so well known that this same formula can be used to find the multiplicative inverse in the domain of modular arithmetic on integers! For example, to find the multiplicative inverse of 3, modulo 256, start with x₀ = 1 (any odd number will do). Then,

The iteration has reached a fixed point modulo 256, so -85, or 171, is the multiplicative inverse of 3 (modulo 256). All calculations can be done modulo 256.

Why does this work? Because if x_n satisfies

and if x_{n + 1} is defined by (31), then

To see this, let dx_n = 1 + km. Then

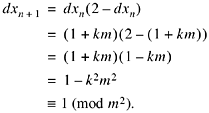
In our application, m is a power of 2, say 2^N. In this case, if

In a sense, if x_n is regarded as a sort of approximation to d?/span>, then each iteration of (31) doubles the number of bits of "accuracy" of the approximation.

It happens that, modulo 8, the multiplicative inverse of any (odd) number d is d itself. Thus, taking x₀ = d is a reasonable and simple initial guess at d?/span>. Then, (31) will give values of x₁, x₂, ? such that

Thus, four iterations suffice to find the multiplicative inverse modulo 2³² (if x 1 (mod 2⁴⁸) then x 1 (mod 2ⁿ) for n 48). This leads to the C program in Figure 10-5, in which all computations are done modulo 2³².

Figure 10-5 Multiplicative inverse modulo 2³² by Newton's method.

unsigned mulinv(unsigned d) {       // d must be odd. 
   unsigned xn, t; 
 
   xn = d; 
loop: t = d*xn; 
      if (t == 1) return xn; 
      xn = xn*(2 - t); 
      goto loop; 
} 

For about half the values of d, this program takes 4 1/2 iterations, or nine multiplications. For the other half (those for which the initial value of xn is "correct to 4 bits"—that is, d² 1 (mod 16)), it takes seven or fewer, usually seven, multiplications. Thus, it takes about eight multiplications on average.

A variation is to simply execute the loop four times, regardless of d, perhaps "strung out" to eliminate the loop control (eight multiplications). Another variation is to somehow make the initial estimate x₀ "correct to 4 bits" (that is, find x₀ that satisfies dx₀ 1 (mod 16)). Then, only three loop iterations are required. Some ways to set the initial estimate are

Here, the multiplication by 2 is a left shift, and the computations are done modulo 2³² (ignoring overflow). Because the second formula uses a multiplication, it saves only one.

This concern about execution time is of course totally unimportant for the compiler application. For that application, the routine would be so seldom used that it should be coded for minimum space. But there may be applications in which it is desirable to compute the multiplicative inverse quickly.

Sample Multiplicative Inverses

We conclude this section with a listing of some multiplicative inverses in Table 10-3.

Table 10-3. Sample Multiplicative Inverses
d	d?/span>
(dec)	mod 16 (dec)	mod 2^32 (hex)	mod 2^64 (hex)
-7	-7	49249249	9249249249249249
-5	3	33333333	3333333333333333
-3	5	55555555	5555555555555555
-1	-1	FFFFFFFF	FFFFFFFFFFFFFFFF
1	1	1	1
3	11	AAAAAAAB	AAAAAAAAAAAAAAAB
5	13	CCCCCCCD	CCCCCCCCCCCCCCCD
7	7	B6DB6DB7	6DB6DB6DB6DB6DB7
9	9	38E38E39	8E38E38E38E38E39
11	3	BA2E8BA3	2E8BA2E8BA2E8BA3
13	5	C4EC4EC5	4EC4EC4EC4EC4EC5
15	15	EEEEEEEF	EEEEEEEEEEEEEEEF
25		C28F5C29	8F5C28F5C28F5C29
125		26E978D5	1CAC083126E978D5
625		3AFB7E91	D288CE703AFB7E91

You may notice that in several cases (d = 3, 5, 9, 11), the multiplicative inverse of d is the same as the magic number for unsigned division by d (see Section 10-14, "Sample Magic Numbers," on page 189). This is more or less a coincidence. It happens that for these numbers, the magic number M is equal to the multiplier m, and these are of the form (2^p + 1)/d, with p 32. In this case, notice that

so that M d?/span> (mod 2³²).