11-1 Integer Square Root

By the "integer square root" function, we mean the function To extend its range of application and to avoid deciding what to do with a negative argument, we assume x is unsigned. Thus, 0 x 2³² - 1.

Newton's Method

For floating-point numbers, the square root is almost universally computed by Newton's method. This method begins by somehow obtaining a starting estimate g₀ of Then, a series of more accurate estimates is obtained from

The iteration converges quadratically—that is, if at some point is accurate to n bits, then g_{n + 1} is accurate to 2n bits. The program must have some means of knowing when it has iterated enough, so it can terminate.

It is a pleasant surprise that Newton's method works fine in the domain of integers. To see this, we need the following theorem:

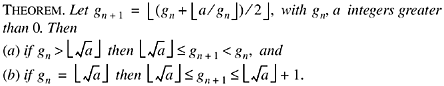
That is, if we have an integral guess g_n to that is too high, then the next guess g_{n + 1} will be strictly less than the preceding one, but not less than Therefore, if we start with a guess that's too high, the sequence converges monotonically. If the guess then the next guess is either equal to g_n or is 1 larger. This provides an easy way to determine when the sequence has converged: If we start with convergence has occurred when g_{n + 1} g_n, and then the result is precisely g_n.

The case a = 0, however, must be treated specially, because this procedure would lead to dividing 0 by 0.

Proof. (a) Because g_n is an integer,

Because and g_n is an integer, Define e by Then e > 0 and

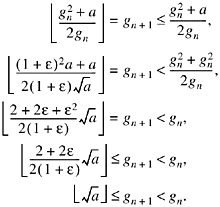
(b) Because so that Hence we have

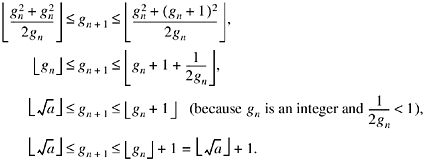
The difficult part of using Newton's method to calculate is getting the first guess. The procedure of Figure 11-1 sets the first guess g₀ equal to the least power of 2 that is greater than or equal to For example, for x =4, g₀ = 2, and for x = 5, g₀ = 4.

Figure 11-1 Integer square root, Newton's method.

int isqrt(unsigned x) {
   unsigned x1; 
   int s, g0, g1; 
 
   if (x <= 1) return x; 
   s = 1; 
   x1 = x - 1; 
   if (x1 > 65535) {s = s + 8; x1 = x1 >> 16;} 
   if (x1 > 255)   {s = s + 4; x1 = x1 >> 8;} 
   if (x1 > 15)  ?{s = s + 2; x1 = x1 >> 4;} 
   if (x1 > 3)     {s = s + 1;} 
 
   g0 = 1 << s;              ?// g0 = 2**s. 
   g1 = (g0 + (x >> s)) >> 1;?// g1 = (g0 + x/g0)/2. 
 
   while (g1 < g0) {           // Do while approximations 
      g0 = g1;                 // strictly decrease. 
      g1 = (g0 + (x/g0)) >> 1; 
   } 
   return g0; 
} 

Because the first guess g₀ is a power of 2, it is not necessary to do a real division to get g₁; instead, a shift right suffices.

Because the first guess is accurate to about 1 bit, and Newton's method converges quadratically (the number of bits of accuracy doubles with each iteration), one would expect the procedure to converge within about five iterations (on a 32-bit machine), which requires four divisions (because the first iteration substitutes a shift right). An exhaustive experiment reveals that the maximum number of divisions is five, or four for arguments up to 16,785,407.

If number of leading zeros is available, then getting the first guess is very simple: Replace the first seven executable lines in the procedure above with

if (x <= 1) return x; 
s = 16 - nlz(x - 1)/2; 

Another alternative, if number of leading zeros is not available, is to compute s by means of a binary search tree. This method permits getting a slightly better value of g₀: the least power of 2 that is greater than or equal to For some values of x, this gives a smaller value of g₀, but a value large enough so that the convergence criterion of the theorem still holds. The difference in these schemes is illustrated below.

Range of x for Figure 11-1	Range of x for Figure 11-2	First Guess g0
0	0	0
1	1 to 3	1
2 to 4	4 to 8	2
5 to 16	9 to 24	4
17 to 64	25 to 80	8
65 to 256	81 to 288	16
?/p>	?/p>	?/p>
2^28 + 1 to 2^30	(2^14 + 1)^2 to (2^15 + 1)^2 - 1	2^15
2^30 + 1 to 2^32 - 1	(2^15 + 1)^2 to 2^32 - 1	2^16

This procedure is shown in Figure 11-2. It is convenient there to treat small values of x (0 x 24) specially, so that no divisions are done for them.

Figure 11-2 Integer square root, binary search for first guess.

int isqrt(unsigned x) {
   int s, g0, g1; 
 
   if (x <= 4224) 
      if (x <= 24) 
         if (x <= 3) return (x + 3) >> 2; 
         else if (x <= 8) return 2; 
         else return (x >> 4) + 3; 
      else if (x <= 288) 
         if (x <= 80) s = 3; else s = 4; 
      else if (x <= 1088) x = 5; else s = 6; 
   else if (x <= 1025*1025 - 1) 
      if (x <= 257*257 - 1) 
         if (x <= 129*129 - 1) s = 7; else s = 8; 
      else if (x <= 513*513 - 1) s = 9; else s = 10; 
   else if (x <= 4097*4097 - 1) 
      if (x <= 2049*2049 - 1) s = 11; else s = 12; 
   else if (x <= 16385*16385 - 1) 
      if (x <= 8193*8193 - 1) s = 13; else s = 14; 
   else if (x <= 32769*32769 - 1) s = 15; else s = 16; 
   g0 = 1 << s;              ?// g0 = 2**s. 
 
   // Continue as in Figure 11-1. 

The worst-case execution time of the algorithm of Figure 11-1, on the basic RISC, is about 26 + (D + 6)n cycles, where D is the divide time in cycles and n is the number of times the while-loop is executed. The worst-case execution time of Figure 11-2 is about 27 + (D + 6)n cycles, assuming (in both cases) that the branch instructions take one cycle. The table below gives the average number of times the loop is executed by the two algorithms, for x uniformly distributed in the indicated range.

x	Figure 11-1	Figure 11-2
0 to 9	0.80	0
0 to 99	1.46	0.83
0 to 999	1.58	1.44
0 to 9999	2.13	2.06
0 to 2^32 - 1	2.97	2.97

If we assume a divide time of 20 cycles and x ranging uniformly from 0 to 9999, then both algorithms execute in about 81 cycles.

Binary Search

Because the algorithms based on Newton's method start out with a sort of binary search to obtain the first guess, why not do the whole computation with a binary search? This method would start out with two bounds, perhaps initialized to 0 and 2¹⁶. It would make a guess at the midpoint of the bounds. If the square of the midpoint is greater than the argument x, then the upper bound is changed to be equal to the midpoint. If the square of the midpoint is less than the argument x, then the lower bound is changed to be equal to the midpoint. The process ends when the upper and lower bounds differ by 1, and the result is the lower bound.

This avoids division, but requires quite a few multiplications?6 if 0 and 2¹⁶ are used as the initial bounds. (The method gets one more bit of precision with each iteration.) Figure 11-3 illustrates a variation of this procedure, which uses initial values for the bounds that are slight improvements over 0 and 2¹⁶. The procedure shown in Figure 11-3 also saves a cycle in the loop, for most RISC machines, by altering a and b in such a way that the comparison is b a rather than b - a 1.

Figure 11-3 Integer square root, simple binary search.

int isqrt(unsigned x) {
   unsigned a, b, m;          ?// Limits and midpoint. 
 
   a = 1; 
   b = (x >> 5) + 8;          ?// See text. 
   if (b > 65535) b = 65535; 
   do {
    ?m = (a + b) >> 1; 
      if (m*m > x) b = m - 1; 
      else         a = m + 1; 
   } while (b >= a); 
   return a - 1; 
} 

The predicates that must be maintained at the beginning of each iteration are and The initial value of b should be something that's easy to compute and close to Reasonable initial values are x, x ?4 + 1, x ?8 + 2, x ?16 + 4, x ?32 + 8, x ?64 + 16, and so on. Expressions near the beginning of this list are better initial bounds for small x, and those near the end are better for larger x. (The value x ?2 + 1 is acceptable, but probably not useful, because x ?4 + 1 is everywhere a better or equal bound.)

Seven variations on the procedure shown in Figure 11-3 can be more or less mechanically generated by substituting a + 1 for a, or b - 1 for b, or by changing m = (a + b) ?2 to m = (a + b + 1) ?2, or some combination of these substitutions.

The execution time of the procedure shown in Figure 11-3 is about 6 + (M + 7.5)n, where M is the multiplication time in cycles and n is the number of times the loop is executed. The table below gives the average number of times the loop is executed, for x uniformly distributed in the indicated range.

x	Average Number of Loop Iterations
0 to 9	3.00
0 to 99	3.15
0 to 999	4.68
0 to 9999	7.04
0 to 2^32 - 1	16.00

If we assume a multiplication time of 5 cycles and x ranging uniformly from 0 to 9999, the algorithm runs in about 94 cycles. The maximum execution time (n = 16) is about 206 cycles.

If number of leading zeros is available, the initial bounds can be set from

b = (1 << (33 - nlz(x))/2) - 1; 
a = (b + 3)/2; 

That is, These are very good bounds for small values of x (one loop iteration for 0 x 15), but only a moderate improvement, for large x, over the bounds calculated in Figure 11-3. For x in the range 0 to 9999, the average number of iterations is about 5.45, which gives an execution time of about 74 cycles, using the same assumptions as above.

A Hardware Algorithm

There is a shift-and-subtract algorithm for computing the square root that is quite similar to the hardware division algorithm described in Figure 9-2 on page 149. Embodied in hardware on a 32-bit machine, this algorithm employs a 64-bit register that is initialized to 32 0-bits followed by the argument x. On each iteration, the 64-bit register is shifted left two positions, and the current result y (initially 0) is shifted left one position. Then 2y + 1 is subtracted from the left half of the 64-bit register. If the result of the subtraction is nonnegative, it replaces the left half of the 64-bit register, and 1 is added to y (this does not require an adder, because y ends in 0 at this point). If the result of the subtraction is negative, then the 64-bit register and y are left unaltered. The iteration is done 16 times.

This algorithm was described in 1945 [JVN].

Perhaps surprisingly, this process runs in about half the time of that of the 64 ?32 32 hardware division algorithm cited, because it does half as many iterations and each iteration is about equally complex in the two algorithms.

To code this algorithm in software, it is probably best to avoid the use of a doubleword shift register, which requires about four instructions to shift. The algorithm in Figure 11-4 [GLS1] accomplishes this by shifting y and a mask bit m to the right. It executes in about 149 basic RISC instructions (average). The two expressions y | m could also be y + m.

Figure 11-4 Integer square root, hardware algorithm.

int isqrt(unsigned x) {
   unsigned m, y, b; 
 
   m = 0x40000000; 
   y = 0; 
   while(m != 0) {            ?// Do 16 times. 
      b = y | m; 
      y = y >> 1; 
      if (x >= b) {
         x = x - b; 
         y = y | m; 
      } 
      m = m >> 2; 
   } 
   return y; 
} 

The operation of this algorithm is similar to the grade-school method. It is illustrated below, for finding on an 8-bit machine.

?011 0011?x0   Initially, x = 179 (0xB3). 
- 1         b1 
 ————————— 
?111 0011?x1   0100 0000?y1 
- 101       b2   0010 0000?y2 
 ————————— 
?010 0011?x2   0011 0000?y2 
-?11 01  ?b3   0001 1000?y3 
 ————————— 
?010 0011?x3   0001 1000?y3   (Can't subtract). 
-   1 1001?b4   0000 1100?y4 
 ————————— 
?000 1010?x4   0000 1101?y4 

The result is 13 with a remainder of 10 left in register x.

It is possible to eliminate the if x >= b test by the usual trickery involving shift right signed 31. It can be proved that the high-order bit of b is always zero (in fact, b 5 ?2²⁸), which simplifies the x >= b predicate (see page 22). The result is that the if statement group can be replaced with

t = (int)(x | ~(x - b)) >> 31;   // -1 if x >= b, else 0. 
x = x - (b & t); 
y = y | (m & t); 

This replaces an average of three cycles with seven, assuming the machine has or not, but it might be worthwhile if a conditional branch in this context takes more than five cycles.

Somehow it seems that it should be easier than some hundred cycles to compute an integer square root in software. Toward this end, we offer the expressions below to compute it for very small values of the argument. These can be useful to speed up some of the algorithms given above, if the argument is expected to be small.

The expression	is correct in the range	and uses this many instructions (full RISC).
x	0 to 1	0
x > 0	0 to 3	1
	0 to 3	2
	0 to 3	2
	0 to 5	2
	1 to 8	2
	4 to 15	2
(x > 0) + (x > 3)	0 to 8	3
(x > 0) + (x > 3) + (x > 8)	0 to 15	5

Ah, the elusive square root,

It should be a cinch to compute.

But the best we can do

Is use powers of two

And iterate the method of Newt!