12-2 Base -1 + i

By using - 1 + i as the base, where i is all complex integers (complex numbers with integral real and imaginary parts) can be expressed as a single "number" without an explicit sign or other irregularity. Surprisingly, this can be done using only 0 and 1 for digits, and all integers are represented uniquely. We will not prove this or much else about this number system, but will just describe it very briefly.

It is not entirely trivial to discover how to write the integer 2. ^[1] However, this can be determined algorithmically by successively dividing 2 by the base and recording the remainders. What does a "remainder" mean in this context? We want the remainder after dividing by - 1 + i to be 0 or 1, if possible (so that the digits will be 0 or 1). To see that it is always possible, assume that we are to divide an arbitrary complex integer a + bi by - 1 + i. Then, we wish to find q and r such that q is a complex integer, r = 0 or 1, and

^[1] The interested reader might warm up to this challenge.

where q_r and q_i denote the real and imaginary parts of q, respectively. Equating real and imaginary parts and solving the two simultaneous equations for q gives

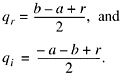
Clearly, if a and b are both even or are both odd, then by choosing r = 0, q is a complex integer. Furthermore, if one of a and b is even and the other is odd, then by choosing r = 1, q is a complex integer.

Thus, the integer 2 can be converted to base - 1 + i by the plan illustrated below.

Because the real and imaginary parts of the integer 2 are both even, we simply do the division, knowing that the remainder will be 0:

Because the real and imaginary parts of - 1 - i are both odd, again we simply divide, knowing that the remainder is 0:

Because the real and imaginary parts of i are even and odd, respectively, the remainder will be 1. It is simplest to account for this at the beginning by subtracting 1 from the dividend.

Because the real and imaginary parts of 1 are odd and even, the next remainder will be 1. Subtracting this from the dividend gives

Because we have reached a 0 quotient, the process terminates, and the base - 1 + i representation for 2 is seen to be 1100 (reading the remainders upwards).

Table 12-3 shows how each bit pattern from 0000 to 1111 is interpreted in base - 1 + i, and how the real integers in the range -15 to +15 are represented.

The addition rules for base - 1 + i (in addition to the trivial ones involving a 0 bit) are as follows:

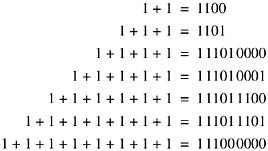
Table 12-3. Conversions between Decimal and Base -1 + I
n (base -1 + i)	n (decimal)	n (decimal)	n (base -1 + i)	-n (base -1 + i)
0	0	0	0	0
1	1	1	1	11101
10	-1 + i	2	1100	11100
11	i	3	1101	10001
100	-2i	4	111010000	10000
101	1 - 2i	5	111010001	11001101
110	-1 - i	6	111011100	11001100
111	-i	7	111011101	11000001
1000	2 + 2i	8	111000000	11000000
1001	3 + 2i	9	111000001	11011101
1010	1+ 3i	10	111001100	11011100
1011	2 + 3i	11	111001101	11010001
1100	2	12	100010000	11010000
1101	3	13	100010001	1110100001101
1110	1 + i	14	100011100	1110100001100
1111	2 + i	15	100011101	1110100000001

When adding two numbers, the largest number of carries that occurs in one column is six, so the largest sum of a column is 8 (111000000). This makes for a rather complicated adder. If one were to build a complex arithmetic machine, it would no doubt be best to keep the real and imaginary parts separate, ^[2] with each represented in some sensible way such as two's-complement.

^[2] This is the way it was done at Bell Labs back in 1940 on George Stibitz's Complex Number Calculator [Irvine].