13-1 Gray Code

Is it possible to cycle through all 2ⁿ combinations of n bits by changing only one bit at a time? The answer is "yes," and this is the defining property of Gray codes. That is, a Gray code is an encoding of the integers such that a Gray-coded integer and its successor differ in only one bit position. This concept can be generalized to apply to any base, such as decimal, but here we will discuss only binary Gray codes.

Although there are many binary Gray codes, we will discuss only one: the "reflected binary Gray code." This code is what is usually meant in the literature by the unqualified term "Gray code." We will show, usually without proof, how to do some basic operations in this representation of integers, and we will show a few surprising properties.

The reflected binary Gray code is constructed as follows. Start with the strings 0 and 1, representing the integers 0 and 1:

Reflect this about a horizontal axis at the bottom of the list, and place a 1 to the left of the new list entries, and a 0 to the left of the original list entries:

This is the reflected binary Gray code for n = 2. To get the code for n = 3, reflect this and attach a 0 or 1 as before:

From this construction, it is easy to see by induction on n that (1) each of the 2ⁿ bit combinations appears once and only once in the list, (2) only one bit changes in going from one list entry to the next, and (3) only one bit changes when cycling around from the last entry to the first. Gray codes having this last property are called "cyclic," and the reflected binary Gray code is necessarily cyclic.

If n > 2, there are non-cyclic codes that take on all 2ⁿ values once and only once. One such code is 000 001 011 010 110 100 101 111.

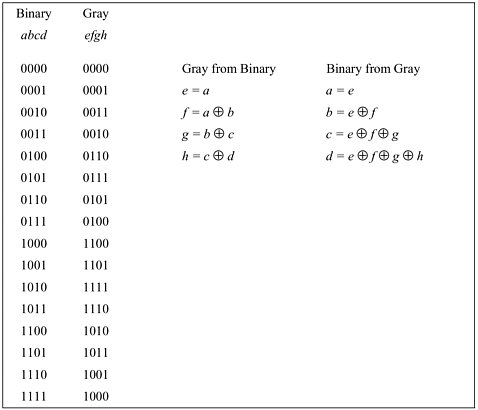
Figure 13-1 shows, for n = 4, the integers encoded in ordinary binary and in Gray code. The formulas show how to convert from one representation to the other at the bit-by-bit level (as it would be done in hardware).

Figure 13-1. 4-bit Gray code and conversion formulas.

As for the number of Gray codes on n bits, notice that one still has a cyclic binary Gray code after rotating the list (starting at any of the 2ⁿ positions and cycling around) or reordering the columns. Any combination of these operations results in a distinct code. Therefore, there are at least 2ⁿ ?n! cyclic binary Gray codes on n bits. There are more than this for n 3.

The Gray code and binary representations have the following dual relationships, evident from the formulas given in Figure 13-1:

?span style='font:7.0pt "Times New Roman"'>         Bit i of a Gray-coded integer is the parity of bit i and the bit to the left of i in the corresponding binary integer (using 0 if there is no bit to the left of i).

?span style='font:7.0pt "Times New Roman"'>         Bit i of a binary integer is the parity of all the bits at and to the left of position i in the corresponding Gray-coded integer.

Converting to Gray from binary can be done in only two instructions:

The conversion to binary from Gray is harder. One method is given by

We have already seen this formula in "Computing the Parity of a Word" on page 74. As mentioned there, this formula can be evaluated as illustrated below for n = 32.

B = G ^ (G >> 1); 
B = B ^ (B >> 2); 
B = B ^ (B >> 4); 
B = B ^ (B >> 8); 
B = B ^ (B >> 16); 

Thus, in general it requires instructions.

Because it is so easy to convert from binary to Gray, it is trivial to generate successive Gray-coded integers:

for (i = 0; i < n; i++) {
   G = i ^ (i >> 1); 
   output G; 
}