14-6 Other Space-Filling Curves

As was mentioned, Peano was first, in 1890, to discover a space-filling curve. The many variations discovered since then are often called "Peano curves." One interesting variation of Hilbert's curve was discovered by Eliakim Hastings Moore in 1900. It is "cyclic" in the sense that the end point is one step away from the starting point. The Peano curve of order 3, and the Moore curve of order 4, are shown in Figure 14-13. Moore's curve has an irregularity in that the order 1 curve is up-right-down but this shape does not appear in the higher-order curves. Except for this minor exception, the algorithms for dealing with Moore's curve are very similar to those for the Hilbert curve.

Figure 14-13. Peano (left) and Moore (right) curves.

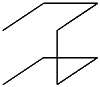
The Hilbert curve has been generalized to arbitrary rectangles and to three and higher dimensions. The basic building block for a 3-dimensional Hilbert curve is shown below. It hits all eight points of a 2x2x2 cube. These and many other space-filling curves are discussed in [Sagan].