15-1 IEEE Format

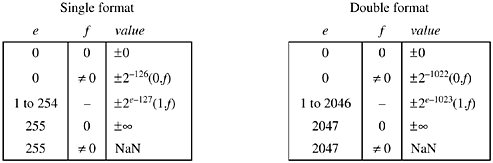
We will restrict our attention to the single and double formats (32- and 64-bit) described in IEEE 754. The standard also describes "single extended" and "double extended" formats, but they are only loosely described because the details are implementation-dependent (e.g., the exponent width is unspecified in the standard). The single and double formats are shown below.

The sign bit s is encoded as 0 for plus, 1 for minus. The biased exponent e and fraction f are magnitudes with their most significant bits on the left. The floating-point value represented is encoded as shown on the next page.

As an example, consider encoding the number p in single format. In binary [Knu1],

This is in the range of the "normalized" numbers shown in the third row of the table above. The most significant 1 in p is dropped, as the leading 1 is not stored in the encoding of normalized numbers. The exponent e - 127 should be 1, to get the binary point in the right place, and hence e = 128. Thus, the representation is

0 10000000 10010010000111111011011 

or, in hexadecimal,

40490FDB, 

where we have rounded the fraction to the nearest representable number.

Numbers with 1 e 254 are called "normalized numbers." These are in "normal" form, meaning that their most significant bit is not explicitly stored. Nonzero numbers with e = 0 are called "denormalized numbers," or simply "denorms." Their most significant bit is explicitly stored. This scheme is sometimes called "gradual underflow." Some extreme values in the various ranges of floating-point number are shown in Table 15-1. In this table "Max integer" means the largest integer such that all integers less than or equal to it, in absolute value, are representable exactly; the next integer is rounded.

For normalized numbers, one unit in the last position (ulp) has a relative value ranging from 1/2²⁴ to 1/2³³ (about 5.96 x 10^-8 to 1.19 x 10^-7) for single format, and from 1/2⁵³ to 1/2⁵² (about 1.11 x 10^-16 to 2.22 x 10^-16) for double format. The maximum "relative error," for round to nearest mode, is half of those figures.

The range of integers that is represented exactly is from -2²⁴ to +2²⁴ (-16,777,216 to +16,777,216) for single format, and from -2⁵³ to =2⁵³ (-9,007,119,254,740,992 to +9,007,199,254,740,992) for double format. Of course, certain integers outside these ranges, such as larger powers of 2, can be represented exactly; the ranges cited are the maximal ranges for which all integers are represented exactly.

Table 15-1. Extreme Values
Single Precision
	Hex	Exact Value	Approximate Value
Smallest denorm	0000 0001	2^-149	1.401x10^-45
Largest denorm	007F FFFF	2^-126(1 - 2^-23)	1.175x10^-38
Smallest normalized	0080 0000	2^-126	1.175x10^-38
1.0	3F80 0000	1	1
Max integer	4B80 0000	2^24	1.677x10^7
Largest normalized	7F7F FFFF	2^128(1 - 2^-24)	3.403x10^38
	7F80 0000
Double Precision
Smallest denorm	0 0001	2^-1074	4.941x10^-324
Largest denorm	000F F	2^-1022(1 - 2^-52)	2.225x10^-308
Smallest normalized	0010 0	2^-1022	2.225x10^-308
1.0	3FF0 0	1	1
Max integer	4340 0	2^53	9.007x10^15
Largest normalized	7FEF F	2^1024(1 - 2^-53)	1.798x10^308
	7FF0 0

One might want to change division by a constant to multiplication by the reciprocal. This can be done with complete (IEEE) accuracy only for numbers whose reciprocals are represented exactly. These are the powers of 2 from 2^-127 to 2¹²⁷ for single format, and from 2^-1023 to 2¹⁰²³ for double format. The numbers 2^-127 and 2^-1023 are denormalized numbers, which are best avoided on machines that implement operations on denormalized numbers inefficiently.