16-4 Formulas for Other Difficult Functions

Let us have a closer look at what Willans and Wormell have done. We postulate the rules below as defining what we mean by the class of functions that can be represented by "formulas," which we will call "formula functions." Here, x?/span> is shorthand for x₁, x₂, ? x_n for any n 1. The domain of values is the integers ?-2, -1, 0, 1, 2, ?

1. The constants ?-1, 0, 1, ?are formula functions.

2. The projection functions f(x?/span>) = x_i, for 1 i n, are formula functions.

3. The expressions x + y, x - y, and xy are formula functions, if x and y are.

4. The class of formula functions is closed under composition (substitution). That is, f(g₁(x?/span>), g₂(x?/span>), ? g_m(x?/span>)) is a formula function if f and g_i are, for i = 1, ? m.

5. Bounded sums and products, written

are formula functions, if a, b, and f are, and a(x?/span>) b(x?/span>).

Sums and products are required to be bounded to preserve the computational character of formulas; that is, formulas can be evaluated by plugging in values for the arguments and carrying out a finite number of calculations. The reason for the prime on the S and P is explained later in this chapter.

When forming new formula functions using composition, we supply parentheses when necessary according to well-established conventions.

Notice that division is not included in the list above; that's too complicated to be uncritically accepted as a "formula function." Even so, the above list is not minimal. It might be fun to find a minimal starting point, but we won't dwell on that here.

This definition of "formula function" is close to the definition of "elementary function" given in [Cut]. However, the domain of values used in [Cut] is the non-negative integers (as is usual in recursive function theory). Also, [Cut] requires the bounds on the iterated sum and product to be 0 and x - 1 (where x is a variable), and allows the range to be vacuous (in which case the sum is defined as 0 and the product is defined as 1).

In what follows, we show that the class of formula functions is quite extensive, including most of the functions ordinarily encountered in mathematics. But it doesn't include every function that is easy to define and has an elementary character.

Our development is slightly encumbered, compared to similar developments in recursive function theory, because here variables can take on negative values. However, the possibility of a value's being negative can often be accommodated by simply squaring some expression that would otherwise appear in the first power. Our insistence that iterated sums and products not be vacuous is another slight encumbrance.

Here, a "predicate" is simply a 0/1-valued function, whereas in recursive function theory a predicate is a true/false-valued function, and every predicate has an associated "characteristic function" that is 0/1-valued. We associate 1 with true and 0 with false, as is universally done in programming languages and in computers (in what their and and or instructions do); in logic and recursive function theory, the association is often the opposite.

The following are formula functions:

1. a² = aa, a³ = aaa, and so on.

2. The predicate a =b:

3. (a b) = 1 - (a = b).

4. The predicate a b:

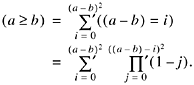
We can now explain why we do not use the convention that a vacuous iterated sum/product has the value 0/1. If we did, we would have such shams as

The comparison predicates are key to everything that follows, and we don't wish to have them based on anything quite that artificial.

5. (a > b) = (a b + 1).

6. (a b) = (b a).

7. (a < b) = (b > a).

8. |a| = (2(a 0) - 1)a.

9. max(a, b) = (a b) (a - b) + b.

10. min(a, b) = (a b) (b - a) + a.

Now we can fix the iterated sums and products so that they give the conventional and useful result when the range is vacuous.

11.

12.

From now on we will use S and P without the prime. All functions thus defined are total (defined for all values of the arguments).

13.

This gives n! = 1 for n 0.

In what follows, P and Q denote predicates.

14. ?span class=docemphasis1>P(x?/span>) = 1 - P(x?/span>).

15. P(x?/span>) & Q(x?/span>) = P(x?/span>)Q(x?/span>).

16. P(x?/span>) | Q(x?/span>) = 1 - (1 - P(x?/span>))(1 - Q(x?/span>)).

17. P(x?/span>) Q(x?/span>) = (P(x?/span>) - Q(x?/span>))².

18. if P(x?/span>) then f(y?/span>) else g(z?/span>) = P(x?/span>)f(y?/span>) + (1 - P(x?/span>))g(z?/span>).

19.

This gives, arbitrarily and perhaps incorrectly for a few cases, the result 0 for n < 0, and the result 1 for 0⁰.

20.

21.

is vacuously true, Ǝ is vacuously false.

22.

The value of this expression is the least x in the range m to n such that the predicate is true, or m if the range is vacuous, or n + 1 if the predicate is false throughout the (nonvacuous) range. The operation is called "bounded minimalization" and it is a very powerful tool for developing new formula functions. It is a sort of functional inverse, as illustrated by the next formula. That minimalization can be done by a sum of products is due to Goodstein [Good].

23.

This is the "integer square root" function, which we define to be 0 for n < 0, just to make it a total function.

24. d/n = (-|n| q |n|)(n = qd).

This is the "d divides n" predicate, according to which 0|0 but ?0|n) for n 0.

25. n ?d = if n 0 then (-n min q n)(0 r |d| - 1)(n = qd + r) else (n min q -n)(-|d| + 1 r 0)(n = qd + r).

This is the conventional truncating form of integer division. For d = 0 it gives a result of |n| + 1, arbitrarily.

26. rem(n, d) = n - (n ?d)d.

This is the conventional remainder function. If rem(n, d) is nonzero, it has the sign of the numerator n. If d = 0, the remainder is n.

27. isprime(n) = n 2 & ?2 d |n| - 1)(d/n).

28.

(Number of primes n.)

29. p_n = (1 min k 2ⁿ)(p(k) = n).

30. exponent(p, n) = (0 min x |n|)?p^{x + 1}|n).

This is the exponent of a given prime factor p of n, for n 1.

31. For n 0.

32. The nth digit after the decimal point in the decimal expansion of

Thus, the class of formula functions is quite large. It is limited, though, by the following theorem (at least):

Theorem. If f is a formula function, then there is a constant k such that

where there are k 2's.

This can be proved by showing that each application of one of the rules 1-5 (on page 279) preserves the theorem. For example, if f(x?/span>) = c (rule 1), then for some h,

where there are h 2's. Therefore,

because For so the theorem holds with k = 0.

For rule 3, let

Then, clearly

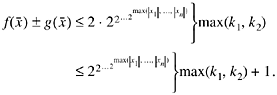
Similarly, it can be shown that the theorem holds for f(x, y) = xy.

The proofs that rules 4 and 5 preserve the theorem are a bit tedious but not difficult, and are omitted.

From the theorem, it follows that the function

Equation 4

is not a formula function, because for sufficiently large x, Equation (4) exceeds the value of the same expression with any fixed number k of 2's.

For those interested in recursive function theory, we point out that Equation (4) is primitive recursive. Furthermore, it is easy to show directly from the definition of primitive recursion that formula functions are primitive recursive. Therefore, the class of formula functions is a proper subset of the primitive recursive functions. The interested reader is referred to [Cut].

In summary, this section shows that not only is there a formula in elementary functions for the nth prime, but also for a good many other functions encountered in mathematics. Furthermore, our "formula functions" are not based on trigono-metric functions, the floor function, absolute value, powers of -1, or even division. The only sneaky maneuver is to use the fact that the product of a lot of numbers is 0 if any one of them is 0, which is used in the formula for the predicate a = b

It is true, however, that once you see them, they are not interesting. The quest for "interesting" formulas for primes should go on. For example, [Rib] cites the amazing theorem of W. H. Mills (1947) that there exists a q such that the expression

is prime-valued for all n 1. Actually, there are an infinite number of such values (e.g., 1.3063778838⁺ and 1.4537508625483⁺). Furthermore, there is nothing special about the "3"; the theorem is true if the 3 is replaced with any integer 3 (for different values of q). Better yet, the 3 can be replaced with 2 if it is true that there is always a prime between n² and (n + 1)², which is almost certainly true, but has never been proved. And furthermore, ?well, the interested reader is referred to [Rib] and to [Dud] for more fascinating formulas of this type.