The .NET Framework Class Library contains a number of generic classes readily available for you. You can also define your own generic classes, which is what you will do in this section. Before we do this, I will provide a bit of background theory.
In the following exercises, you will define and use a class that represents a binary tree. This is a very practical exercise because this class happens to be one that is missing from the System.Collections.Generic namespace. A binary tree is a very useful data structure used for a variety of operations, including sorting and searching through data very quickly. There are volumes written on the minutiae of binary trees, but it is not the purpose of this book to cover binary trees in detail. Instead, we will just look at the pertinent details. If you are interested you should consult a book such as The Art of Computer Programming, Volume 3: Sorting and Searching by Donald E. Knuth (Addison-Wesley Professional; 2nd edition 1998).
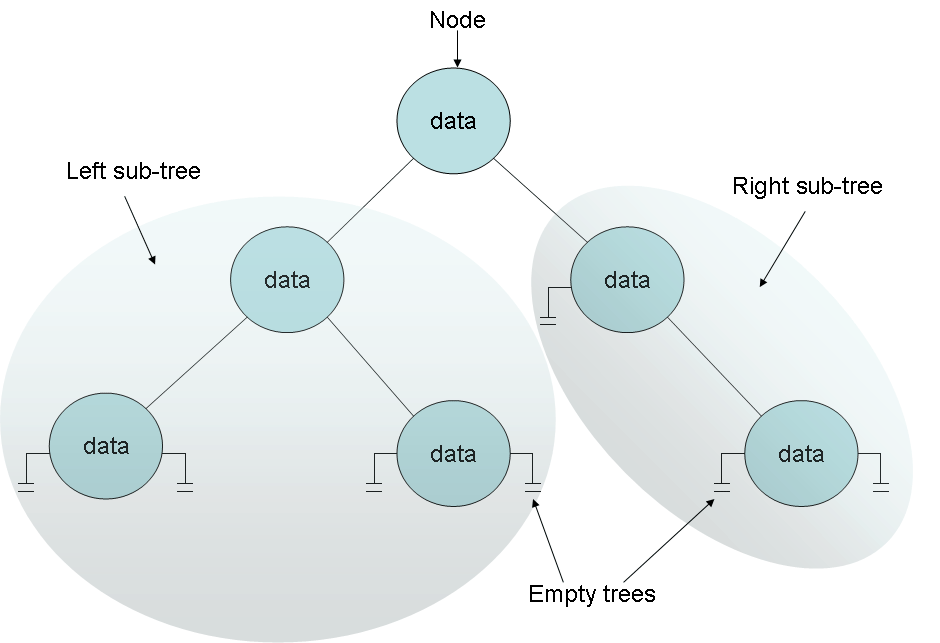
A binary tree is a recursive (self-referencing) data structure that can either be empty or comprise three elements: some data that is typically referred to as the node and two sub-trees, which are themselves binary trees. The two sub-trees are conventionally called the left sub-tree and the right sub-tree because they are typically depicted to the left and right of the node respectively. Each left sub-tree or right sub-tree is either empty, or contains a node and other sub-trees. In theory, the whole structure can continue ad infinitum. Figure 17-1 shows the structure of a small binary tree.
The real power of binary trees becomes evident when you use them for sorting data. If you start with an unordered sequence of objects of the same type, you can use them to construct an ordered binary tree and then walk through the tree to visit each node in an ordered sequence. The algorithm for inserting an item into an ordered binary tree is shown below:
If the tree, T, is empty Then Construct a new tree T with the new item I as the node, and empty left and right sub-trees Else Examine the value of the node, N, of the tree, T If the value of N is greater than that of the new item, I Then If the left sub-tree of T is empty Then Construct a new left sub-tree of T with the item I as the node, and empty left and right sub-trees Else Insert I into the left sub-tree of T End If Else If the right sub-tree of T is empty Then Construct a new right sub-tree of T with the item I as the node, and empty left and right sub-trees Else Insert I into the right sub-tree of T End If End If End If
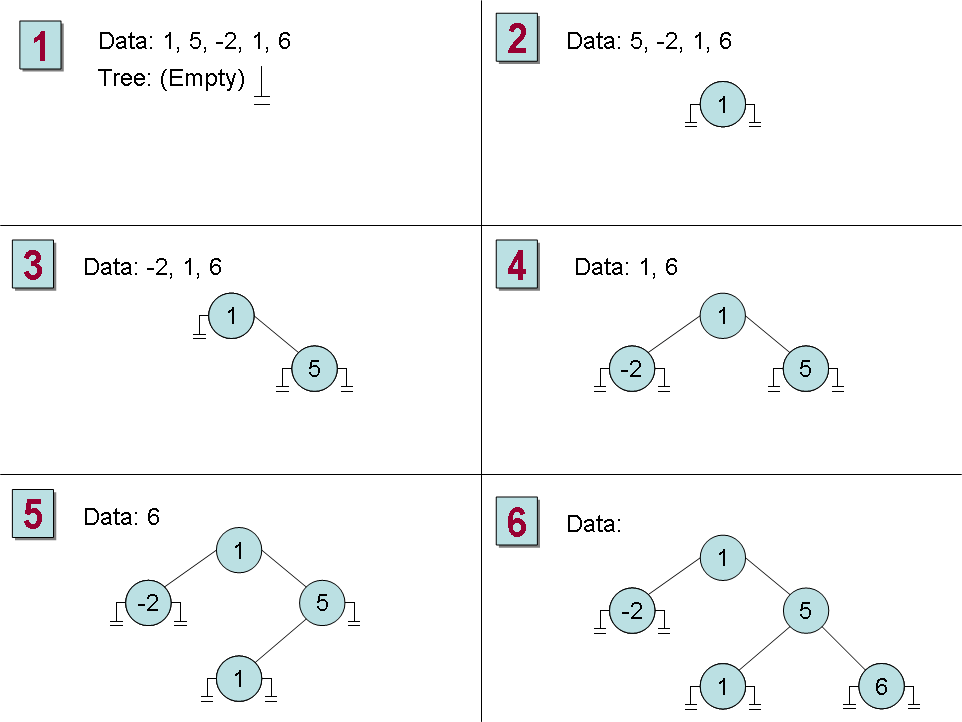
Notice that this algorithm is recursive, calling itself to insert the item into the left or right sub-tree depending on the value of the item and the current node in the tree.
If you start with an empty binary tree and an unordered sequence of objects, you can iterate through the unordered sequence inserting each one into the binary tree by using this algorithm, resulting in an ordered tree. Figure 17-2 shows the steps in the process for constructing a tree from a set of 5 integers.
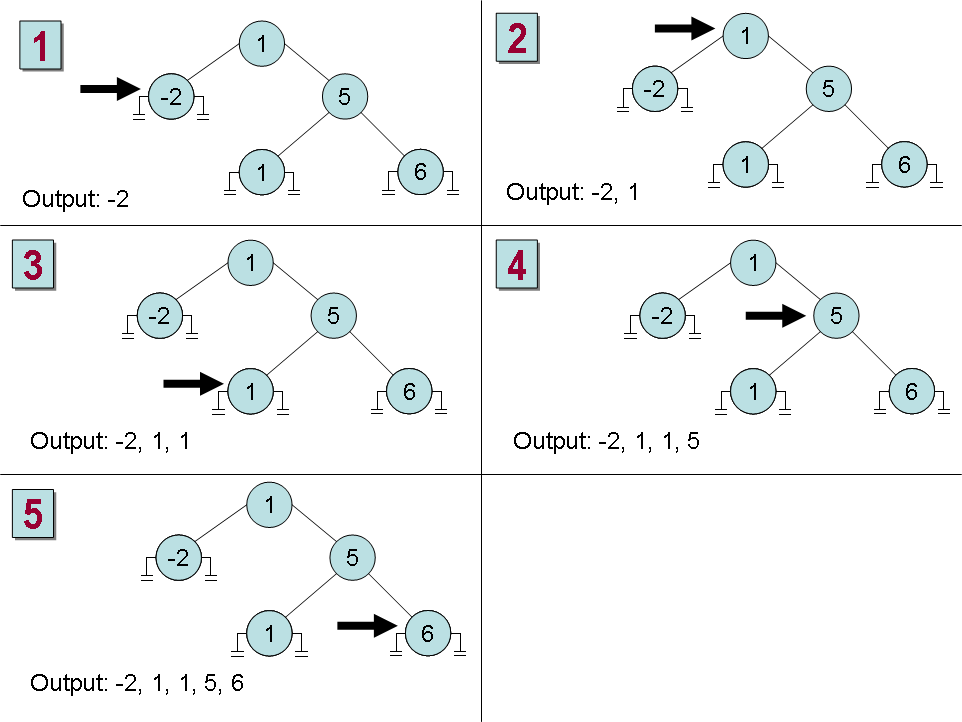
Once you have built an ordered binary tree, you can display its contents in sequence by visiting each node in turn and printing the value found. The algorithm for achieving this task is also recursive:
If the left sub-tree is not empty Then Display the contents of the left sub-tree End If Display the value of the node If the right sub-tree is not empty Then Display the contents of the right sub-tree End If
Figure 17-3 shows the steps in the process for outputting the tree constructed earlier. Notice that the integers are now displayed in ascending order.
In the following exercise, you will use generics to define a binary tree class capable of holding almost any type of data. The only restriction is that the data type must provide a means of comparing values between different instances.
The binary tree class is a class that you might find useful in many different applications. Therefore, you will implement it as a class library rather than an application in its own right. You can then reuse this class elsewhere without needing to copy the source code and recompile it. A class library is a set of compiled classes (and other types such as structs and delegates) stored in an assembly. An assembly is a file that usually has the “.dll” suffix. Other projects and applications can make use of the items in a class library by adding a reference to its assembly, and then bringing its namespaces into scope with using statements. You will do this when you test the binary tree class.
Start Visual Studio 2005.
Create a new Visual C# project using the Class Library template (on the File menu, point to New, and then click Project). Name the project BinaryTree and set the Location to \Microsoft Press\Visual CSharp Step By Step\Chapter 17.
In the Solution Explorer change the name of the file Class1.cs to Tree.cs.
In the Code and Text Editor window, change the definition of the Class1 class to Tree<T>.
The definition of the Tree<T> class should look like this:
public class Tree<T>
{
...
}
In the Code and Text Editor window, modify the definition of the Tree<T> class to specify that the type parameter T must denote a type that implements the generic IComparable<T> interface.
The modified definition of the Tree<T> class should look like this:
public class Tree<T> where T : IComparable<T>
{
...
}
Add three private variables to the Tree<T> class; a T variable called data, and two Tree<T> variables called left and right:
private T data; private Tree<T> left; private Tree<T> right;
Add a constructor to the Tree<T> class that takes a single T parameter called nodeValue. In the constructor, set the data variable to nodeValue, and initialize the left and right variables to null, as shown below:
public Tree(T nodeValue)
{
this.data = nodeValue;
this.left = null;
this.right = null;
}
Add a public property of type T called NodeData to the Tree<T> class. This property should provide get and set accessors allowing the user to read and modify the data variable:
The NodeData property should look like this:
public T NodeData
{
get { return this.data; }
set { this.data = value; }
}
Add two more properties to the Tree<T> class called LeftTree and RightTree. These properties are very similar to each other, and provide get and set access to the left and right Tree<T> variables respectively.
The LeftTree property should look like this (the RightTree property is the same except that it uses the right variable):
public Tree<T> LeftTree
{
get { return this.left; }
set { this.left = value; }
}
Add a public method called Insert to the Tree<T> class. This method will insert a T value into the tree.
The method definition should look like this:
public void Insert (T newItem)
{
}
The Insert method will follow the algorithm described earlier. The programmer will have used the constructor to insert the initial node into the tree, so the Insert method can assume that the tree is not empty. The next part of the algorithm is reproduced below to help you understand the code you will write in the following steps:
... Examine the value of the node, N, of the tree, T If the value of N is greater than that of the new item, I Then If the left sub-tree of T is empty Then Construct a new left sub-tree of T with the item I as the node, and empty left and right sub-trees Else Insert I into the left sub-tree of T End If ...
In the Insert method, add a statement that declares a local variable of type T, called currentNodeValue. Initialize this variable to the value of the NodeData property of the tree, as shown below:
public void Insert(T newItem)
{
T currentNodeValue = this.NodeData;
}
Add the following if-else statement to the Insert method, after the definition of the currentNodeValue variable. This statement uses the CompareTo method of the IComparable<T> interface to determine whether the value of the current node is greater then the new item:
if (currentNodeValue.CompareTo(newItem) > 0)
{
//Insert the new item into the left sub-tree
}
else
{
// Insert the new item into the right sub-tree
}
Replace the //Insert the new item into the left sub-tree comment with the following block of code:
if (this.LeftTree == null)
{
this.LeftTree = new Tree<T>(newItem);
}
else
{
this.LeftTree.Insert(newItem);
}
These statements check whether the left sub-tree is empty. If so, a new left sub-tree is created using the new item; otherwise the new item is inserted into the existing left sub-tree by calling the Insert method recursively.
Replace the //Insert the new item into the right sub-tree comment with the equivalent code that inserts the new node into the right sub-tree:
if (this.RightTree == null)
{
this.RightTree = new Tree<T>(newItem);
}
else
{
this.RightTree.Insert(newItem);
}
Add another public method called WalkTree to the Tree<T> class. This method will walk through the tree, visiting each node in sequence and printing out its value.
The method definition should look like this:
public void WalkTree()
{
}
Add the following statements to the WalkTree method. These statements implement the algorithm described earlier for printing the contents of a binary tree:
if (this.LeftTree != null)
{
this.LeftTree.WalkTree();
}
Console.WriteLine(this.NodeData.ToString());
if (this.RightTree != null)
{
this.RightTree.WalkTree();
}
On the Build menu, click Build Solution. The class should compile cleanly, so correct any errors that are reported and rebuild the solution if necessary.
In the next exercise, you will test the Tree<T> class by creating binary trees of integers and strings.
On the File menu, point to Add and then click New Project. Add a new project using the Console Application template. Name the project BinaryTreeTest and set the Location to \Microsoft Press\Visual CSharp Step By Step\Chapter 17.
Ensure the BinaryTreeTest project is selected in the Solution Explorer. On the Project menu, click Set as Startup Project. The BinaryTreeTest project will be highlighted in the Solution Explorer.
When you run the application, this is the project that will actually be executed.
On the Project menu, click Add Reference. In the Add Reference dialog box, click the Projects tab. Click the BinaryTree project and then click OK.
The BinaryTree assembly will appear in the list of references for the BinaryTreeTest project in the Solution Explorer. You will now be able to create Tree<T> objects in the BinaryTreeTest project.
In the Code and Text Editor window displaying the Program class, add the following using directive to the list at the top of the class:
using BinaryTree;
Add the following statements to the Main method:
Tree<int> tree1 = new Tree<int>(10); tree1.Insert(5); tree1.Insert(11); tree1.Insert(5); tree1.Insert(-12); tree1.Insert(15); tree1.Insert(0); tree1.Insert(14); tree1.Insert(-8); tree1.Insert(10); tree1.Insert(8); tree1.Insert(8); tree1.WalkTree();
These statements create a new binary tree for holding ints. The constructor creates an initial node containing the value 10. The Insert statements add nodes to the tree, and the WalkTree method prints out the contents of the tree, which should be sorted in ascending order.
On the Build menu, click Build Solution. Verify that the solution compiles, correcting any errors if necessary.
On the Debug menu, click Start Without Debugging.
When the program runs, the values should be displayed in the following sequence:
–12, –8, 0, 5, 5, 8, 8, 10, 10, 11, 14, 15
Press the Enter key to return to Visual Studio 2005.
Add the following statements to the end of the Main method, after the existing code:
Tree<string> tree2 = new Tree<string>("Hello");
tree2.Insert("World");
tree2.Insert("How");
tree2.Insert("Are");
tree2.Insert("You");
tree2.Insert("Today");
tree2.Insert("I");
tree2.Insert("Hope");
tree2.Insert("You");
tree2.Insert("Are");
tree2.Insert("Feeling");
tree2.Insert("Well");
tree2.WalkTree();
These statements create another binary tree for holding strings, populate it with some test data, and then print the tree. This time, the data will be sorted alphabetically.
On the Build menu, click Build Solution. Verify that the solution compiles, correcting any errors if necessary.
On the Debug menu, click Start Without Debugging.
When the program runs, the integer values will be displayed as before followed by the strings in the following sequence:
Are, Are, Feeling, Hello, Hope, How, I, Today, Well, World, You, You
Press the Enter key to return to Visual Studio 2005.