Self-reference is not without its pitfalls. You have most likely encountered the frustration of circular definitions in the dictionary, such as "Fashion pertains to style" and "Style pertains to fashion." From this you conclude that "Fashion pertains to fashion." This kind of self-reference conveys no information; it is to be avoided. "This sentence is false" is another type of self-reference to be avoided, for it tells us nothing. If true it must be false, and if false it must be true. Nevertheless, self-reference is an important technique in finding and expressing solutions to problems.
Recall that the top-down approach to problem solving entails breaking down an initial problem into smaller component problems. These components need not be related except in the sense that putting their solutions together yields a solution to the original problem. If any of these component problems is identical in structure to the initial problem, the solution is said to be recursive and the problem is said to be solved by recursion. If the solution and its components are functionally modularized, then the solution will refer to itself. Recursion is thus a special case of the top-down design methodology.
Suppose a traveler asks you, "How do I get there from here?" You might respond with a complete set of directions, but if the directions are too complex, or you are not sure, your response might be: "Go to the main street, turn left, continue for one mile, and then ask, "How do I get there from here?" This is an example of recursion. The traveler wanted directions to a destination. In solving the problem, you provided an initial small step leading toward the traveler's goal. After taking that step, the traveler will be confronted with a new version of the original problem. This new problem, while identical in form to the original, involves a new starting location closer to the destination.
Cursing is often used to belittle a problem; recursing has the same effect! Recursion, when appropriate, can give relatively easy-to-understand and concise descriptions for complex tasks. Still, care must be taken in its use, or else efficiency of storage and execution time will be sacrificed.
4.2: Using Recursion
Applying the recursive method is just like applying the top-down approach, but it can be tricky; it presents conceptual difficulties for many students. The purpose of this section is to show how to develop and understand recursive solutions. Some illustrative examples are provided to help you get the idea. Practice will help you become skilled in the use of recursion.
4.2.1 The Towers of Hanoi
A game called the Towers of Hanoi was purportedly played by priests in the Temple of Brahma, who believed that completion of the game's central task would coincide with the end of the world. The task involves three pegs. The version considered here has n disks initially mounted on peg 1 (the priests dealt with 64 disks). The n disks increase in size from top to bottom, the top disk being the smallest. The problem is to relocate the n disks to peg 3 by moving one at a time. Only the top disk on a peg can be moved. Each time a disk is moved it may be placed only on an empty peg or on top of a pile of disks of larger size. The task is to develop an algorithm specifying a solution to this problem, no matter what the value of n.
Consider the case when n = 4, shown in Figure 4.1(a). The following sequence of instructions provides a solution.
1. Move the top disk from peg l to peg 2.
2. Move the top disk from peg 1 to peg 3.
3. Move the top disk from peg 2 to peg 3.
4. Move the top disk from peg 1 to peg 2.
5. Move the top disk from peg 3 to peg 1.
6. Move the top disk from peg 3 to peg 2.
7. Move the top disk from peg 1 to peg 2.
8. Move the top disk from peg 1 to peg 3.
9. Move the top disk from peg 2 to peg 3.
10. Move the top disk from peg 2 to peg 1.
11. Move the top disk from peg 3 to peg 1.
12. Move the top disk from peg 2 to peg 3.
13. Move the top disk from peg 1 to peg 2.
14. Move the top disk from peg 1 to peg 3.
15. Move the top disk from peg 2 to peg 3.
It is not difficult to arrive at such a solution for a specific small value of n. Try to find a solution for n = 5. You will find that, even though you succeed after some trial and error, creating a solution for n = 25 is indeed a formidable task. You may even be too old to care by the time you finish. If a particular value of n gives so much trouble, how does one specify a solution for any n, when one does not even know what value n will have?
One answer is to apply the technique of recursion. This means attempting to break down the problem into component problems that can be solved directly or that are identical to the original problem but involve a smaller number of disks. The three component problems below fit the requirements of this framework.
1. Move the top n - 1 disks from peg 1 to peg 2.
2. Move the top disk from peg 1 to peg 3.
3. Move the top n - 1 disks from peg 2 to peg 3.
If these three problems can be solved, and their solutions are applied in sequence to the initial situation, then the result is a solution to the original problem. This can be seen from parts (a)-(d) of Figure 4.1, which show the consecutive situations after each is applied.
We now generalize the original problem:
Move the top n disks from peg i to peg f.
i denotes the initial peg on which the top n disks to be relocated reside, and f denotes the final peg to which they are to be relocated. Let a denote the third available peg. Solving the original problem, which has only n disks, is equivalent to solving the generalized problem with i taken as 1 and f taken as 3. This is because the moves that accomplish its solution will also work for the generalized problem, since any disks below the top n are larger than they are, so their existence doesn't render any of the moves illegal. Solving the first component problem is equivalent to solving the generalized problem with n replaced by n - 1, i by 1, and â by 2. It is now apparent that the original problem, and the components 1, 2, and 3, have structure identical to the generalized problem, but the components involve fewer disks. They also involve different initial, available, and final pegs. This is why it was necessary to generalize the original problem.
Suppose you have found a solution to the generalization and denote it by towers(n,i,a,f). Then, as just shown, the application of the solutions to components 1, 2, and 3, in sequence, will be a solution to the original problem. A recursive definition for towers(n,i,a,f) can now be expressed as follows. Note that moves in towers(n,i,a,f) are from peg i to peg f--that is, from the second parameter to the fourth parameter. The first parameter specifies the number of top disks, on the peg given by the second parameter, that are to be moved.
This is the recursive algorithm for the Towers of Hanoi problem. Notice that the definition gives an explicit solution for the special case when n = l and an implicit solution for the case of n > 1.
To use the method of recursion we must recognize when it is applicable and find a correct way to generalize the original problem and then to break down the generalization. We have been successful and have found a recursive algorithm. Because no further refinement is needed, the corresponding recursive program can be written directly using functional modularization:
[1]
[2]
The labels [1] and [2] are not part of the program but are used later as references when explaining the program. It is essential to see that this function has been written just like any other; whenever a component task is available as a function, we invoke it to carry out that task. The feature that distinguishes it and makes it a recursive function is that the required functions happen to be the function itself. The references within towers to itself are allowed in recursive languages.
Anytime a function calls itself during its execution, a recursive call has been made. The two invocations of towers within towers represent such recursive calls. In general, when a recursive program executes on a computer, or when its execution is simulated, many recursive calls will be made. Simulation of a program or function call means carrying out its instructions by hand and keeping track of the values of all its variables. These are referred to as the first, second, etc., recursive calls. The initial call to the function precedes the first recursive call.
The verification of a recursive program can be done in two ways, as is true for a nonrecursive program. One is by formal proof, the other by checking all cases. With recursion, the cases given explicitly are checked first. A case is given explicitly when the action taken by the program in that case does not require a recursive call. Also, it is assumed that each function individually works correctly. For towers(n,i,a,f), the only explicit case is when n = 1 and the function clearly outputs the proper result and terminates.
For the case when n exceeds l, Figure 4.1 has already confirmed that as long as the three component functions work properly, then towers(n,i,a,f) will also. Note that these components correspond to smaller values of n. Mathematically inclined readers may recognize that this really amounts to a proof of correctness for towers using mathematical induction on n. One of the advantages of recursive programs is that they may be proven correct more easily in this way.
In order to understand how a recursive program actually executes, it is necessary to simulate its execution. Below are the first few steps of the simulation for a call to towers(n,i,a,f) with the values 4, 1, 2, 3 -- that is, towers(4,1,2,3). It will soon become apparent that considerable bookkeeping is involved, requiring an organized way to do it.
Since n is greater than 1, the procedure requires the sequential execution of
and
To do this requires suspending the execution of towers(4,1,2,3) at this point in order to simulate the first recursive call, towers(3,1,3,2). Note that after this recursive call is completed, 1
Dealing with towers(3,1,3,2), since n > 1, the commands
and
must be carried out sequentially. Now the execution of towers(3,1,3,2) must be suspended in order to simulate the second recursive call, towers(2,1,2,3). Note that after this recursive call is completed, 1
Dealing with towers(2,1,2,3), since n > 1,
and
must be carried out sequentially. These two calls to towers represent the third and fourth recursive calls. They both complete without generating any new recursive calls. The three statements result in the outputting of l
Enough is enough! At this point you may feel like a juggler with too few hands and too many recursive calls. Figure 4.2 represents a convenient way to keep track of the complete simulation; it may be generated as the simulation proceeds. The figure traces the recursive calls made to towers as the initial call to towers(4,1,2,3) is executed to completion. Each recursive call is numbered to show whether it is the first, second, . . . , or fourteenth. The bracketed return values indicate the labeled statement of procedure towers at which the preceding recursive call is to resume when the next call is completed. For example, when towers(3,1,3,2) is completed, towers(4,1,2,3) resumes at [l]. Our simulation stopped just as the fifth recursive call was to be carried out. The figure uses shorthand for the output. For example, l
Figure 4.2 indicates very clearly what information must be available at each point in the simulation (or execution of the program) in order to carry it out. Specifically, it is necessary to know the following information:
The four parameter values of the call currently being carried out
Where to resume when the call currently being carried out is completed
For example, when the third recursive call is completed, resumption must be at the printf statement of the second recursive call; when the fifth recursive call is completed, resumption must be at the end of the first recursive call; and finally, after the initial recursive call is completed, resumption must be at the proper point in the program that called towers originally.
Notice that the last three parameters are never modified by towers, but the first parameter, which corresponds to the number of disks for the current problem, is modified. For instance, the first recursive call to towers(3,1,3,2) has modified the first parameter, making it 3 rather than 4 as it was initially. It is important that this modification be kept local to towers(3,1,3,2), not reflected back to towers(4,1,2,3), the initial call.
It is not always possible to find a recursive solution to a problem, nor is it always desirable to use one when available. Sometimes a recursive solution is the only one we can find. For the Towers of Hanoi problem it is difficult to find a nonrecursive solution, but a number are known. Recursive solutions normally make it easier to see why they are correct, probably because to achieve them requires that you make the structure inherent in the problem more explicit.
To make this point clearly, the recursive algorithm and a nonrecursive algorithm are repeated here. Convince yourself that the nonrecursive algorithm solves the Towers of Hanoi problem correctly (see Exercise 8). The nonrecursive program is taken from Walsh [1982]; another nonrecursive program appears in Buneman and Levy [1980].
A Recursive Solution for the Towers of Hanoi
A Nonrecursive Algorithm for the Towers of Hanoi
l. Label the disks l, 2, . . . , n in increasing order of size.
2. Label the pegs i, a, and f, n + 1, n + 2, and n + 3, respectively.
3. Move the smallest disk onto another disk with an even label or onto an empty peg with an even label.
4. While all disks are not on the same peg
a. move the second smallest top disk onto the peg not containing the smallest disk
b. move the smallest disk onto another disk with an even label or onto an empty peg with an even label.
The Tower of Babel failed for lack of communication. The construction workers did not speak the same language. While recursion allows the solution to the Towers of Hanoi to be specified conveniently, it is execution time that causes trouble. The diagram of Figure 4.1 shows that the construction of the new tower of disks will take 24 - 1 or fifteen moves. It is not difficult to generalize the diagram to n disks to conclude that 2n - 1 moves will be needed for n disks (see Exercise 7). Even with Olympic-caliber construction workers, it would take over one thousand years to complete the tower for 50 disks.
We will now present a series of functions to further illustrate recursive programs. The functions
1. Determine the length of a list
2. Create a list that is a copy of another list
3. Count checkerboard placements
4. Generate all permutations of n integers and process each one. (This is applied to the stable marriage problem.)
In addition to providing repetition so that you can become more familiar with and understand recursion better, the examples provide a background to show how local and global variables and parameters are treated in recursive programs and why recursive solutions are not always the best. A list may be thought of as being either a null list or as one record followed by another list (the link field of the record plays the role of the head of this other list). This is nothing but a way to define a list recursively. Consider the recursive function defined by
This function returns the length of the list, listname. To verify that this is correct we must check
1. The null list. It returns with length = 0.
2. A one-record list followed by another list. It returns length = 1 + the length of the list after the first record.
It is correct, since its value is correct for each case. Of course it is correct--after all, the length of a null list is zero, and the length of a list with at least one record is 1 for the record, plus the length of the rest of the list beyond the first record ! This was how length was written in the first place.
Consider the function copy, which creates a list second that is a copy of a list first:
When first is the null list, copy faithfully terminates with the copy also a null list. When first is a one-record list, copy sets second to point to storage allocated for a record and sets the information field value of this record to the value of the information field in first's first record. The recursive call to copy(next(first),&rest) is then an invocation of copy to copy the null list, since next(first) is null in this case. Assuming it performs its task correctly, rest will be null when it returns. The link field of the record pointed to by second is then set to the value of rest (the null pointer), and the initial call to copy terminates correctly.
Similarly, had there been more than one record in first's list, the recursive call to copy would have returned with rest pointing to a correct copy of the list pointed to by next(first). Setlink would correctly place a pointer to that correct copy into the link field of the record pointed to by second, and the initial call would terminate correctly. This verifies that copy is correct in all cases. Again, to copy the null list is easy. To copy a list with at least one record, simply copy that record, copy the rest of the list beyond the first record, and append that copy to the copy of the first record. This is how copy was written!
If you are confronted with a recursive program and want to understand it, approach it in the same way as you would a nonrecursive program. Assume that any functions that are called perform their functions correctly, and then attempt to see what the program itself does. Sometimes this will be apparent, as it was for towers and copy, and sometimes a simulation of the program helps to increase comprehension. Imagine, for example, that you were not told what copy did. It wouldn't have been so easy to find out without simulating some simple cases.
In order to understand what happens as a recursive program executes, it is necessary to review how local and global variables are treated, and also how parameters are treated. This must also be known to understand what happens when any program executes.
In nonrecursive programs, references to global and to static variables always refer to the current actual storage assigned to them. Hence any changes to their values during execution of the program will be reflected back in their values. Local automatic variables are treated differently. Local copies are made, and these are referred to during the execution of the function to which they are local. If the local variables are automatic, the storage for the local copies disappears when the function terminates or returns. If the local variables are static, the storage remains after the function is terminated, and the variable retains its value for the next time the function is called.
This situation holds for recursion also. Each recursive call to a function produces its own copies of automatic local variables. Thus there may be many different values for the same local variable--each applicable to its own invocation of the function. As with nonrecursion, there is only one storage allocation for a global or a static variable, and it holds the last value of the variable.
Parameters passed in the argument lists of functions are treated as variables local to the function. They are passed by value. New storage is established for each parameter. The storage is initially set to the value of the corresponding actual parameter when the function is invoked. In effect, this storage represents a local copy of the actual parameter. Any reference in the function is interpreted as a reference to the local copy only. This implies that any change to a parameter during the execution of the function will not be reflected back to the storage used for the actual parameter; it can not have its value changed by the function.
The only way to change the original value of a variable used as a parameter is to pass the address of the parameter instead of its value. This is done automatically in the case of arrays and character strings. When an array is passed as a parameter, the address of the first storage location in the array is passed. This negates the need to make local copies of all the values of the array in the function and thus waste memory. Addresses for parameters can also be passed as pointers A copy is made in the function and is local to the function. Using the pointer, the value of the parameter can be changed.
Here is a simple example.
Suppose that simple is invoked with actual parameters a and b, containing 0 and 1 respectively. It is invoked by the statement, simple (a,&b). Within the function, x initially has a copy of a as its value--0 in this case. y refers to the storage for b--that is, y is a pointer to the storage for b. The first statement of simple causes x to assume the value l, the second statement causes the storage for b to contain 2, and the third statement sets the storage for b to 3. When the calling program continues, a will still be 0, but b will be 3.
Parameters of recursive programs are treated in just this way. Any time cursive call is made within a recursive program, the recursive call acts just like a call to any function. The only difference is that, since a recursive function may generate many recursive calls during its execution, many local copies of its parameters may be produced. References to a parameter by value during the execution of each recursive call will then mean the current local copy of that parameter. Reference to a parameter passed by a pointer to it always means the same actual parameter.
In the recursive version of copy, note that
Null and rest are local variables of the initial call to copy and remain local variables in all subsequent recursive calls. Local copies of null and rest are thus made on any call to copy.
First is passed by value and second by pointer.
Whenever copy is executing and generates a recursive call to copy(next(first),&rest), the actual first parameter of copy is the current copy of next(first)--i.e., the copy associated with the currently executing call to copy. Any references to the first parameter during the generated recursive call refer to the new local copy associated with that call.
When first points to the list as shown in Figure 4.3, and copy(first, second) is executed, the sequence of events and memory configurations that will take place appear in Figure 4.4. First0, first1, first2, first3 refer to the local copies of the actual first parameter associated with the initial, first, second, and third recursive calls to copy, respectively. Similarly for the other variables. A question mark indicates an as yet undefined value. Be sure you understand Figure 4.4 and how it represents the execution of copy.
An alternative version of copy that returns a pointer to the copy of the list first would be as shown on page 160.
This version differs from the original version in two ways. One, it has only one parameter, the list to be copied, and two, it returns a pointer to the new copy rather than setting a second parameter to point to the new copy.
The third example relates to counting squares. Consider an n X n checkerboard and determine the number of ways a 4 X 4 checkerboard can be placed on it. For example, if n = 5, there are four ways to place a 4 X 4 checkerboard on the 5 X 5 board, as shown below.
For this particular example the solution is easy to see by inspection. However, how do you state an algorithm that produces the result in all cases? This can be done handily using recursion. Suppose you know the number of ways, f(n - 1), in which the 4 X 4 board can be placed on an (n - 1) X (n - 1) board. An additional (n - 3) + (n - 4) placements result from an n X n board, because of the n cells
added at the top and left sides of the (n - 1) X (n - 1) board, as shown in Figure 4.5. There are a total of f(n) = f(n - 1) + (n - 3) + (n - 4) placements for the n X n board, when n
It is easy to write a recursive function f, with parameter n, to return the correct result for any n
If n = 7, the program would execute as follows:
A simpler, more direct solution can be obtained by noticing that the top left corner of the 4 x 4 board can be placed in the first, second, . . . , (n - 3)th position of the top row of the n X n board, resulting in (n - 3) different placements. The second row also allows (n - 3) placements. In fact, each of the first (n - 3) rows allows (n - 3) placements, for a total of (n - 3) X (n - 3) distinct placements.Thus f(n) = (n - 3) X (n - 3) for n
The recursive solution will take time and storage O(n), whereas the nonrecursive solution requires constant time and storage. Obviously, this solution is better in every way than the recursive solution to this problem. Hence recursion does not always yield the best solution. Just as with any tool, it must be used judiciously. You wouldn't use a bulldozer to dig a two-foot hole in your yard.
The final example returns to the stable marriage problem. Suppose you are asked to find a stable pairing for the n men and women of the stable marriage problem in Chapter 2, but you aren't aware of the algorithm discussed in Section 2.5. Probably the most straightforward approach is to search through all the possible pairings until a stable pairing is found. Each possible pairing may be thought of as a specific permutation of the n women. Thus the example pairing of Table 2.2 corresponds to the permutation (or listing) 4, 3, 1, 2, 5. In general there are n ! such permutations (where n! means n factorial).
This approach yields a program that traverses the collection of permutations, processing each one and halting when a stable permutation is encountered. Stable may be conveniently invoked to check a permutation for stability. In contrast, the algorithm of Section 2.5 avoids such an exhaustive search by eliminating some permutations from consideration altogether. Still, many problems require just such an exhaustive search and contain a component to produce the permutations. The problem is to write a program to carry out the traversal. The function permutations does this:
where next (n,&done) must return, having updated the current permutation to the next permutation, unless the current permutation is the last one, when it simply sets done to true.
The problem is now to refine next. Suppose n = 4 and the first permutation is 3 2 1. Inserting 4 in all possible positions among 1, 2, and 3 gives the first four permutations of 1, 2, 3, and 4.
Removing 4 leaves 3 2 1. The next four permutations for n = 4 can be obtained by first obtaining the next permutation after 3 2 1 for n = 3. But this next permutation for n = 3 can similarly be obtained by shifting 3 to the right one place, yielding 2 3 1. Then the next four permutations for n = 4 are
Removing 4 leaves 2 3 1. Again, the next permutation after 2 3 1, 2 1 3, is obtained by shifting 3 right. The next four permutations for n = 4 are
Continuing this process will produce, in turn,
Generalizing, we see that, given a permutation of the n integers from 1 to n, the next permutation can be generated by shifting n to the right whenever possible. The only time this is not possible is if n is already at the right end. The next permutation must then be generated by removing n and replacing the leftmost n - 1 integers, which must be a permutation of the integers from 1 to n - 1, by their next permutation. If n is 1, then the last permutation has been produced. This provides a recursive definition for next.
In order to proceed, a data structure to store the permutation must be chosen. To illustrate the effect of this selection, we will use two different structures--arrays and lists. We start by storing the permutation in an array p. Searching for the location of n in p will be avoided by keeping an array l of pointers. Both p and l are defined globally. l[n] points to the location of n in p when next(n,pdone) is invoked. Initialize must set p[i] to n - i + 1 and l[i] to 1 for 1
Figure 4.6(a) simulates the execution of next(4,pdone) when the current permutation is 2 1 3 4.
Now suppose p is implemented as a list whose records are stored in dynamic memory. We need the pointer arrays ptr and pred, which are defined globally, as is the record pointer p. When next(n,pdone) is invoked, ptr[n] will contain a pointer to the record containing n in its information field, and pred[n] will contain a pointer to the predecessor of that record in p. To simplify list shifts and the insertion of a record at the front of p, a dummy record is used as the first record of p. Pred[k] will initially contain a pointer to the dummy record, and ptr[k] will initially contain a pointer to the record of p that contains k, for l
Figure 4.6(b) simulates the execution of next(4,pdone) when the current permutation is 2 l 3 4.
In comparing the two implementations notice that the advantage of the list implementation is that the for loop required by the array implementation is no longer needed. Inserting n at the left end of the current permutation thus takes only two pointer changes rather than time proportional to n. Other permutation algorithms are explored in Sedgewick [1977].
To further illustrate the differences, two complete programs using function permutations, one for the array and one for the list implementation, are given below. The process function prints each permutation. To adapt these programs to obtain a solution for the stable marriage problem, the function process must test for stability. Another modification would be to abort the execution when a stable pairing is found. This requires that process be given access to done so that it can set done to true at that point.
Array Implementation
List Implementation
When any program invokes one of its functions, it is because the task performed by that component must now be carried out. Global variables and variables passed by address (pointers) specify storage that is not local to the component but that it may reference and change. It may also reference and change static variables. All such storage represents the data the component is to process. Any changes by the component to the data are reflected back in the data's storage.
Parameters passed to a function by value also specify storage that is not local to it, but these parameters are treated differently. When the component is invoked, their values are copied into storage that is local to the component. It is these local copies that are referenced, and perhaps changed, by the component as it executes, but such changes are not reflected back to the original values. In this way the information passed by value is made accessible to the component, which may even change the local copies, but such changes are kept local; the original nonlocal values are untouched.
In effect, these copies are treated as if they were additional local variables of the component. The actual local variables of the component represent temporary information that the component uses to do its job. Both the local copies and local variables disappear when the task is completed. This storage for local copies and local variables serves as a "scratchpad" for use by the component. The scratchpad contains information used temporarily by the component to perform its task on the data. This view of the data and scratchpad of a component is depicted in Figure 4.7.
The component may, in turn, invoke another component, which may invoke still another, and so on. Each time this is done, the calling component suspends its operation, so all components of the sequence, except the last, are waiting.
When the last component completes its task, the component that invoked it then continues. In order for this to happen, each component must remember from whence it was called. Also, upon return to the correct place, the scratchpad of the calling component must be the same as before the call. For nonrecursive programs, the important point is that each component must retain only one returning point, and the scratchpad of a component is automatically retained when it invokes another component.
With recursive programs the situation is considerably different, as evidenced by Figures 4.2, 4.4, and 4.6. First, when a recursive function is invoked, this may be the initial, first, second, or nth recursive call to it. If it is the nth recursive call, there may be as many as (n + 1) returning places to be retained, not just one. Second, there may be (n + l) scratchpads to be retained. How many there are is determined by the number of calls that are currently suspended.
Suppose that this number is k, that the return for the initial call is handled separately, and also that the scratchpad for the currently executing call is associated with the function. The number of sets of additional returns and scratchpads that must be retained is then k. The depth of a recursive program is given by the maximum value of k. It is the depth that determines the amount of storage required by the function. The following examples illustrate these ideas.
Example 4.1
In Figure 4.2, when the tenth recursive call (k = 3) is made to towers, there are three returns and three sets of scratchpads to remember in addition to the initial call's return.
n = 1, i = 2, a = 1, f = 3 for the tenth recursive call are stored, by our assumption, local to towers. In general, the depth of recursion will be n - l. Using our terminology, there are no data.
Example 4.2
In Figure 4.4, when the third recursive call is made to copy, there are three returns and three sets of scratchpads to be retained beside the initial call's return:
No returns are shown since they all return to the same place: the statement setlink(*psecond, rest). The depth of the recursion is one less than the length of the list to be copied. The data for the initial call is second, while for the (n + 1)th recursive call it is restn. A change to rest in the (n + 1)th call is reflected in the scratchpad for the nth call. Storage could be saved by making null global to copy.
Example 4.3
In Figure 4.6 the situation corresponds to a point in the initial call when the second and then the third recursive calls to next are made. The local variable i is not shown, and the three scratchpad values are
Again, the returns are all the same, to the statement following the recursive call to next, so they are not shown. The depth of the recursion is n - 1. The data consist of p, ptr, pred, and done.
It should by now be clear that the storage required by a recursive function is proportional to its depth. The execution time, on the other hand, has to do with the total number of recursive calls that are required to complete the initial call. This explains why the recursive solution to Counting Squares (Section 4.2.6) is so inefficient both in time and in storage.
Recursion is a powerful tool for the development of algorithms and leads to concise, clear recursive programs that can be easier to check for correctness. Complex algorithms may be expressed using relatively few program statements, which at the same time emphasize the structure of the algorithm. This will become even more apparent later in the text, as more difficult problems are solved.
A function that invokes itself is directly recursive. A function is indirectly recursive if any sequence of calls to other functions can lead to a call to the original function. Compilers for recursive languages must translate recursive as well as nonrecursive programs. It is not necessary to understand how a recursive program is translated (any more than it is necessary to know how a nonrecursive program is translated) in order to understand or to write the program itself. But it is necessary to know how the program will execute. This amounts to being able to simulate its execution.
The programmer constrained to a nonrecursive language can still use the power of recursion. This is done by writing a program as if the language allowed recursion, and then translating the program into an equivalent nonrecursive program. This is what compilers for recursive languages do and is one reason for spending time finding out how to translate (or implement) a recursive program.
As shown in the discussion of Counting Squares, some problems should not be solved using recursion under any circumstances. Sometimes, as in the Towers of Hanoi problem, we may only be able to think of a recursive solution. Often we can find both a recursive and a nonrecursive solution, which may be compared for trade-offs in clarity, conciseness, storage, and execution time.
Even though a recursive solution may not be best, it may suggest an approach to the problem that otherwise might have been missed and that may turn out to be the most desirable. In fact, the translated version of a recursive solution can often be helpful in finding desirable modifications. This is another reason for looking at the translation process.
Normally, if a recursive approach is right for a problem, and is applied intelligently, further refinements of the program do not improve its efficiency significantly. Breaking up a problem as required by the recursive approach does, however, create the possibility of doing certain tasks in parallel. For instance, the three components of the Towers of Hanoi solution may all be done at the same time with parallel processing. Languages and computer systems that allow concurrent processing will surely become more prevalent. When they do, recursive solutions will have another advantage.
If each successive call to a recursive function were implemented so that during execution a new copy of the function is created with its own storage for the return and its scratchpad values, then, in effect, the function could be treated like any function in a nonrecursive program. With the advent of cheaper and larger storage, this may well occur in the future, but until then, another means of managing the generated returns and scratchpad values is needed.
The essential difference between nonrecursive (or iterative) programs and recursive programs is the storage needed for the returns and scratchpad values of the latter. Figures 4.2, 4.4, and 4.6 actually represent the bookkeeping needed to simulate the execution of a recursive program. The basic idea in translating such programs is to implement this bookkeeping procedure as follows:
1. Each time a recursive call is made to the function,
a. save the proper return place and the current scratchpad values,
b. set the scratchpad values to their new values.
2. Each time a recursive call is completed,
a. restore the current return and scratchpad values to those that were last saved (and save them no longer),
b. return to the proper place in the recursive function, or to the original calling component if it is the initial call that has just finished.
This procedure does not apply to a function that returns a value, but it may be modified to do so. Or the function may be modified to return the value in an additional parameter passed by pointer. As an illustration of this, the first version of copy might be obtained by such a modification of the second.
Notice that the information to be retained (return and scratchpad values) must be recalled in the order opposite to the order in which it is generated. This is no different for nonrecursive programs, except that then the information is saved locally with each component. It is helpful to think of return and scratchpad values as the entries of a record. Then the collection of records corresponding to each suspended recursive call must be stored in some data structure. The data structure must retain not only these records, but also the correct order.
In step 1 above, the record to be saved must become the new first record in the order. In step 2, the current first record (the last saved) must be removed from the data structure. A data structure for storing information so that new information can be inserted, so that a deletion always removes the last piece of information inserted, and which can be tested to see if it is empty (contains no information) is called a stack. Stacks will be discussed in more detail later in the chapter; for now they will simply be used.
The stack is the most convenient data abstraction to use for the bookkeeping recursion entails. To illustrate the translation, and the possibility of enhancing efficiency, the recursive functions towers and next will now be translated into nonrecursive functions.
In towers there are two recursive calls. The idea in implementing it is to write a nonrecursive program that executes just as the recursive program would, while managing the additional records generated by the recursion. This amounts to implementing the procedure described for simulating towers. Each recursive call will be replaced by code to insert the proper return indicator onto a stack, as well as the current scratchpad values. Whenever the end of a recursive call is reached, the proper return indicator and the scratchpad values last put on the stack will be removed and restored to the program's local storage. The earlier recursive version and its implementation as a nonrecursive function are as follows .
Recursive Version
Nonrecursive Version
S_tack is a routine that inserts its arguments, as fields of a record, onto the stack. The name s_tack is used to be sure the compiler can distinguish this routine from the type name stack that also appears in the function. Setstack ensures that the stack will initially contain zero entries; empty returns true if the stack contains no records and false otherwise. The setvar routines do the proper setting of the current scratchpad values for the ensuing recursive call. Restore(&retrn,&n,&i,&a,&f,&s) restores the proper scratchpad values when a return is to be made after completion of some recursive call.
Setvar1(&n,&i,&a,&f) sets n to n - 1 and interchanges the values of f and a.
Setvar2(&n,&i,&a,&f) sets n to n - 1 and interchanges the values of a and i.
The "implicit" exit of the recursive program (after the second recursive call) has been replaced in the implementation by a complex "explicit" sequence of statements. This is because the exit must, in effect, transfer control to the proper place in the calling program. If the stack itself is empty at this point, this means that it is the initial call to towers that has been completed. Return should then be to the calling program. Otherwise, it is some recursive call to towers that has been completed. At this point, the top stack record contains the four scratchpad values to be restored and the return location in towers.
You should simulate the execution of this implementation to see that it really works correctly. The statement labeled "one" corresponds to the first executable statement of the recursive program; this is the statement that is invoked in the implementation to represent a recursive call. It is only invoked, however, after the scratchpad values of the current call and proper return location have been saved on the stack, and the scratchpad values for the upcoming recursive call have been correctly set.
Notice that the implementation requires a stack that can hold the stored information for up to n - 1 recursive calls. The stack must be initialized to empty. Its contents must be preserved between calls. We will not dwell on its implementation details here, but a complete program to test this version is given in Section 4.5.1.
This example highlights the fact that considerable overhead is involved in executing recursive programs. Time is consumed because variables must be stacked and unstacked for each recursive call and its return. It is often possible to discover a more efficient nonrecursive algorithm for a problem, even though the recursive algorithm is evident, as was done in Counting Squares. Nonetheless, the recursive version is frequently clearer, easier to understand, and more concise, as well as easier to verify. Therefore some programmers prefer recursive solutions to problems, even if they are less efficient than the nonrecursive versions.
Another approach is to attempt to increase the efficiency of the iterative program (the implementation) that is translated from a recursive program. This attempt can be made whether or not there is a competing nonrecursive routine.
How can we create a more efficient version of a translated program such as towers? The reason for the stack in the first place is to save return codes and to save scratchpad values that are needed when the suspended call is ready to resume (after the saved values have been unstacked and restored, and the proper program segment is to be executed). If the programmer can determine where the return should be, or what the scratchpad values that are to be restored should be, then this information does not have to be stacked. It may not be necessary to save the values of some other variables. It may also be possible to eliminate some return codes. If no variables need to be saved, and there is only one return code, then the stack itself is not needed. Let us attempt to reach this goal for the implementation of the recursive towers routine.
Notice that in the case statement for retrn at 1, the call to s_tack(2,n,i,a,f,&s) saves the values of the current variables in the suspended call, in order to make the recursive call to towers(n-1,a,i,f). When this new recursive call is completed, these current values will be restored, and the retrn will be 2. The statement labeled "two" will then be executed.
If the stack is empty, the initial call is complete. Otherwise restore will be called immediately and control transferred to the new value of retrn. The current values saved by s_tack(2,n,i,a,f,&s) will never be used, and so need not be saved at all. Thus the call to s_tack( 2,n,i,a,f,&s ) may be eliminated from the program. This means that the only return code appearing will be l in the call to s_tack(1,n,i,a,f,&s). However, the value of retrn after restore is called will always be 1. Therefore, no return code needs to be stored on the stack; the case structure may be removed. Retrn is not needed at all. This new program then looks like the following.
Second Nonrecursive Version
Another improvement can be made by changing the if-else structure to a while loop. Doing so improves the clarity and eliminates the goto:
This yields
Third Nonrecursive Version
5 while loop replaces if-else construct
Finally, the function can be written in more structured form, as follows:
Final Nonrecursive Version
This structured version is more efficient than the compilerlike direct translation because the number of stack operations has been reduced. It is also structured for clarity in reading. Both changes make it a better implementation.
The same approach can now be applied to develop a nonrecursive translation for next.
Nonrecursive Version
"explicit" exit must be made
where setvar(&n,&i) simply sets n to n-1.
The same program can be written in a more structured way. First notice that the statement labeled "two" and the goto "two" statement create a while loop. Introducing that while loop but retaining the structure of "one," the overall structure of the program becomes as follows
Next, the structure of "one" can also be improved, as follows.
The logic of this version is much easier to follow. You can see at a glance that the segment control flows from the top down. It consists of a loop, followed by a decision, followed by a loop. The iterative version of next, translated from the recursive next, and using the improved structure, now becomes as follows:
Second Nonrecursive Version
In general, when the value of a scratchpad variable does not change or does not need to be maintained between recursive calls, it need not be stacked. This is the case with the variable i of next. Also, when there is only one return place from a recursive call, there is no need to stack a return indicator. This is the situation with next. Finally, the value of n varies in a predictable fashion. Its restored value will always be 1 greater than its current value. Thus there is no need to stack n. Each time a recursive call returns, n may be correctly restored by adding 1 to its current value.
Therefore, the stack is unnecessary, since no information must be retained on it. The s_tack function can be removed, setvar can be replaced by the statement n = n-1, and restore can be replaced by the statement n = n+1. Still, the stack controls the second while loop in our translated version. Even though no information needs to be stacked, it is still necessary to know when the stack would have been empty so that the loop may be properly exited.
Notice that the first while loop decreases n by l every time a stack entry would have been made, and the second while increases n by l every time an entry would have been deleted from the stack. Hence, if an integer variable s is set to n initially, prior to the first while loop, the test to see if the stack is empty in the second while loop becomes s = n. The final version of next is an iterative program that has no stack. It is an example of the translated version giving us a better solution. This four-step solution is efficient and is also clear.
1. Set s to n.
2. Set n to the rightmost entry in the permutation that can still be shifted right.
3. If that entry is not l, then
Shift it right
else
Set done to true
4. Place the s-n entries that could not be moved to the right in the proper order at the left end of the permutation.
The final program is as follows:
Final Nonrecursive Version
By translating the recursive solution and analyzing it, a highly efficient nonrecursive solution was built. A little insight can help a lot. For more on recursion, see Barron [1968] and Bird [1977a, 1977b]. It may now be time for you to make a recursive call on all preceding material!
Earlier in this chapter the notion of a stack was introduced and used in the nonrecursive implementations of towers and next. Stacks are useful in situations requiring the retention and recall of information in a specific order--namely, when information is removed in a last-in, first-out order (LIFO for short). Removing tennis balls from a can is LIFO. In programming, stacks are useful when a program must postpone obligations, which must later be fulfilled in reverse order from that in which they were incurred.
Information is kept in order in a stack. Additional information may be inserted on the stack, but only at the front or top end. Thus the information at the top of the stack always corresponds to the most recently incurred obligation. Information may be recalled from the stack, but only by removing the current top piece of information. The stack acts like a pile of playing cards to which we can only add a card at the top and from which we can only remove the top card. Of course, this is not what is meant by a "stacked deck."
The stack, with the operations of front-end insertion and deletion, initialization, and an empty check, is a data abstraction. Stacks used to be called "pushdown stacks"; insertion of data onto the stack was referred to as "pushing" the stack, and deleting data was known as "popping" the stack. So far we have written programs that treat the stack with the four operations as a data abstraction. Stacks will be used frequently in algorithms developed throughout the rest of this book, and it is now time to consider this implementation. Of the many implementations possible for the stack, the following subsections illustrate the three most straightforward.
A stack may be implemented using arrays with the following declarations:
The definitions must be preceded by a typedef for "whatever." Let us assume LIMIT has been set in a define statement fixing the maximum number of items the stack can hold. Suppose 6, 45, 15, 32, and 18 were pushed onto the stack. Figure 4.8 illustrates the meaning attached to the declaration. Figure 4.8(a) is a conceptualization of the stack. Since 6 was the first entry on the stack, it is on the bottom. Likewise, 18 was the last entry, so it is on top. Figure 4.8(b) is the way the data is stored in the actual stack s. The stackarray holds the data and top contains an index to the current entry on the top of the stack. Although 6 is at the top of the array, it is the bottom stack entry; while 18 is at the bottom of the array, it is the top stack entry. Thus top has the value 4.
Addition or insertion of a new element to the stack will be accomplished by a function push. Removal or deletion of the current top stack element will be accomplished by a function pop. Executing push (&newrecord,&s) results in the contents of newrecord being placed on the stack as a new first element. A call to the function pop(&s,&value) causes the removal of the current top stack element, with value containing a copy of that value. A routine setstack sets the stack to empty so that it initially contains no entries.
Example 4.4
Suppose we execute
If Figure 4.8 indicates the current stack, then Figure 4.9 shows the new situation after this execution.
Stack underflow occurs when a program attempts to remove an element from an empty stack. It normally indicates either an error or the termination of a task. Stack overflow occurs when a program attempts to add an element to a full stack. Although, conceptually, the stack as a data structure has no limit, an actual implemented stack does have a limit. In the present implementation it is termed. LIMIT. Push and pop should test, respectively, for stack overflow and underflow and take appropriate action whenever these conditions occur. Such precautionary measures are an example of defensive programming.
It is also necessary to test the stack to determine whether or not it is empty. This may be accomplished by invoking a function empty, which will return the value true when the stack is empty and false otherwise.
These routines may be implemented as follows:
The procedures overflow and underflow are assumed to take appropriate action when they are invoked. Notice that the elements of the stack will be of "whatever" type. We have taken the liberty here of assuming that the C compiler being used allows the contents of one structure to be assigned to another. Otherwise, for example, the assignment
that occurs in push could not be used. Instead, each field of info would have to be individually assigned.
The implementation discussed so far applies when records are to be stored on the stack. Instead, if only the contents of simple variables of type such as int, float, char, or listpointer are to be stored, then the declarations and definitions of push and pop may be simplified, as follows.
"Whatever" will, of course, be declared of type int, or float, etc. The same simplification can be made, when appropriate, to the implementations of Sections 4.5.2, 4.5.3, 4.7.1, 4.7.2, and 4.7.3.
The idea of functional modularity is to isolate or localize the code of a program that is invoked in a particular task, such as an operation on a data structure. The implementation of the stack data abstraction discussed so far has achieved this modularity, with respect to the push, pop, setstack, and empty operations on the stack, by embodying them in individual routines. Another kind of modularity may be achieved by placing the type definitions and the declarations of these operations together in one file. This will be discussed further in the next chapter.
An application of the stack to the nonrecursive towers of Section 4.4.1 follows. It illustrates the use of the stack and its treatment as a data abstraction.
In review of the program, notice that it treates the stack as a data abstraction. The type definitions and function definitions for the stack are placed at the top of the program. The functions setvar, s_tack, and restore are not basic stack operations; they are used by towers. Thus they have been placed after towers. Similarly, towers has been placed after main. Also, s_tack and restore are dependent on the stack implementation, since they must know the structure of a stack record, which is, in turn, determined by the needs of towers for its scratchpad.
In addition to the array implementation, a stack can be implemented as a list. Since we have discussed two ways to implement lists, we know two ways to implement stacks as lists. One is to store the stack records in an array; the other is to store them in dynamic memory. We have already given an implementation of a stack using an array of records in Chapter 3--where availist (Section 3.7) actually acts as a stack. When avail is invoked, it removes the top record from the availist, in addition to returning a pointer to the record. Thus it has effectively popped the record. Likewise, reclaim may return a record to the front of the availist. Doing so, reclaim is essentially pushing a new record onto the availist. Availist serves as the head of a list, which itself serves as a list implementation of a stack. Of course, appropriate overflow and underflow checking must be built into avail and reclaim, respectively.
The third stack implementation is also as a list--one that involves dynamic storage allocation of the records. That is, the records are stored in the storage area set aside by C to store records referenced by pointer variables. First, the following declaration must be made.
If we then define s as type stack, code can be written that is independent of its implementation. Setstack must initialize the stack to empty. This means setting s, the head of the list implementing the stack, to null. Push must now use malloc to allocate storage for the entry to be pushed onto the stack before setting its info field and inserting that record as the new first record on the stack. Pop must copy the info field value of the top record into value and then delete that record from the stack.
These stack operations are implemented as follows.
Notice that this implementation removes the artificial restriction imposed by LIMIT in the first implementation using an array. This is one of the advantages of using dynamic allocation by means of pointer variables.
It is very important to see that no matter what the implementation, as long as the stack is treated as a data abstraction when writing programs, the programs need not be changed, even if the programmer decides to change the implementation of the stack. Only the declarations and definitions related to the stack need be changed, as is evident in the following nonrecursive towers that uses the list implementation. It should be compared to the program of Section 4.5.1, in which the stack was implemented using an array.
The problem of implementing many stacks simultaneously is introduced in the suggested assignment at the end of this chapter. More sophisticated algorithms for the management of the stacks are explored in Garwick [1964], Knuth [1973], and Korsh [1983].
To illustrate the use of stacks, let us consider the problem of evaluating arithmetic expressions. People are accustomed to writing arithmetic expressions in infix notation, where an operator appears between its operands. Consequently, programming languages generally use infix notation to be "user friendly." Thus the programmer can write
(((a + (b/c * d)) + (a/w)) * b)/(((a * c) + d) + a)
Even humans must scan such an expression carefully, more than once, before discovering that its basis syntactic structure is (operand 1)/(operand 2). A serious problem for the compiler writers was how to translate such expressions without making many scans back and forth through them. The problem was compounded further because programmers were not required to write fully parenthesized expressions; this created the additional dilemma of how to resolve ambiguity. As will be shown below, ambiguity may be resolved by using a notation other than infix.
Consider the arithmetic expressions of Table 4.1. These arithmetic expressions are written in prefix, infix, and postfix notation. Prefix means that the operator appears to the left, before its operands, and postfix means that the operator appears to the right, after its operands. Although infix notation is what programmers normally use, there are contexts where prefix (or postfix) notation is used. For instance we write sqrt (x), f(x,y), and minimum (x,y)
Note that the prefix and postfix expressions of the first column are equivalent ways to express the infix expression a + (b * c), while the prefix and postfix expressions of the second column are equivalent to (a + b) * c. Unfortunately, the infix expressions of both columns are identical. This means that, unless parentheses are used, there is no way to distinguish between a + (b * c) and (a + b) * c using infix notation. Yet we can choose the proper prefix or postfix notation to make clear which of the two is intended, even though no parentheses (or special conventions) are used. This holds true in general for arithmetic expressions. For this reason, prefix and postfix notations are called parentheses-free notations. Compilers can easily process prefix and postfix expressions. Since postfix expressions are generally used, they are the main focus of the discussion that follows.
Given an infix expression that is completely parenthesized, such as
you know how to evaluate it. This is because you have grown accustomed to the rules for its evaluation, although you might be hard pressed to state those rules completely and precisely. In any case, parentheses signal how the operators are to be applied to the operands, indicating that (a + b) and (c/d) must be evaluated first before applying the * operator. Removing all parentheses yields
Unless conventions or rules are given, this expression is ambiguous. Its five distinct interpretations correspond to the ways in which parentheses may be placed:
A postfix expression such as
makes little sense, for you are not used to it, having little experience in interpreting or evaluating it. The rule to be used is as follows:
1. Scan the postfix expression from left to right.
2. Whenever an operator is encountered,
replace it, and the immediately preceding number of operands required by that operator, with the result of applying that operator to those operands.
3. Treat this replacement as an operand, and continue scanning from this point.
Thus the postfix expression is equivalent to the infix expression
The rule, in generating this expression, produces the two intermediate expressions: (a + b)cd/*, (a + b)(c/d)*.
The following list shows the five fully parenthesized infix expressions representing the interpretations of a + b * c/d and their corresponding postfix expressions.
These examples emphasize two points:
1. The rule for evaluating postfix expressions allows no ambiguity. It determines precisely the meaning or interpretation of the postfix expression.
2. An infix expression, unless fully parenthesized, may be ambiguous in its meaning or interpretation.
It is because of statement 1 that postfix notation, or postfix expressions, are called parentheses-free. A similar rule allows prefix notation, or prefix expression, to be parentheses-free .
Furthermore, evaluation of a postfix expression is easily accomplished by scanning the expression from left to right and using a stack to retain operands and
results of intermediate evaluations. Any operand that is encountered is placed on an operand stack. When an operator is encountered, its operands are taken from the top of the stack, the operator is applied, and the result is put on the top of the stack. The process is illustrated in the following example.
Example 4.5
Table 4.2 shows the contents of the operand stack after each input is processed, simulating the procedure for evaluation of a postfix expression. The expression is ABC*D/+.
Since the procedure for the evaluation of an arithmetic expression using a stack is relatively straightforward and requires no parentheses, why don't programmers write arithmetic expressions in postfix notation only? It is because they are so used to infix notation that they don't want to change. As a result, high-level languages accept infix expressions rather than postfix. This leads back to the question of how infix expressions may be evaluated.
The rule to be used for a completely parenthesized infix expression is
1. Scan the infix expression from left to right.
2. When a "matched" pair of ''left" and "right" parentheses is encountered,
apply the operator to the operands enclosed within the pair of parentheses, and replace the paired parentheses and the contained operator and operands by the result. Continue scanning from this point.
One problem remains: How do we evaluate infix expressions that are not completely parenthesized? Recall that there are standard rules for interpreting infix expressions in this case. These rules are also incorporated in high-level languages. They are necessary because parentheses are not always available to signal what is to be done next. For example, if we evaluate
then when the * is encountered, the stacks appear as
The operator * signals that, had the expressions been completely parenthesized, a left parenthesis would have occurred just before the b, or else a right parenthesis would have occurred just after the b. In other words, the appearance of the operator requires a decision as to whether b should be considered an operand of *or an operand of +. The standard rules resolve such ambiguities by assigning priorities or precedence values to operators, assuming a left-to-right scan of the expression. For the binary operators, +, -, *, /, and ** (for exponentiation), the priorities are as follows:
1. Exponentiation (**) has the highest priority.
2. Multiplication and division (*, /) have the same priority, which is higher than that of addition or subtraction (+, -).
3. Addition and subtraction (+, -) have the same priority.
A left parenthesis also needs a priority, the lowest.
Whether b is an operand of * or + can then be resolved by taking b as an operand of the highest priority operator (* in this case). Again, parentheses may be used to override priorities. For example, in
b is to be associated with the + operator.
Example 4.6
In order to see how any infix expression is evaluated using priorities, and to develop an algorithm for this evaluation, consider the expression,
To evaluate it, when the first * is encountered the situation will be
In this case, since the left parenthesis is on top of the operator stack, the * should be placed on top of the operator stack, and scanning continued. After c, division(/) is encountered and the stacks become
At this point a decision must be made with respect to c: either it is to be associated with * (at the top of the stack) or with / (the current operator being processed). The standard rules associate c with the operator of highest priority. In this case, since * and / have equal priorities, associate c with the leftmost of the two operators in the input--that is, the top stack operator. Thus, the * must be popped, c and b must be popped, the * must be applied to b and c, and the result, (b * c), placed on top of the operand stack. Then the / must be placed on the operator stack. Had the current operator been of higher priority (say, **), then the current operator should simply be placed on the operator stack.
In the example, after / and d are processed, the stacks are as follows:
The ** becomes the current operator, and d must be associated with it or with /. Since ** has higher priority, place it on the operator stack; the result after processing e is
The current input character being scanned is now a right parenthesis. This "matches" the topmost left parenthesis on the stack. The next steps are to pop the operator stack; pop the operand stack to obtain the top two operands; apply **to them, and place the result back on the top of the operand stack. Then pop the operator stack; pop the operand stack to obtain the top two operands; apply / to them and place the result back on top of the operand stack; pop the stack again; and notice that a left parenthesis has appeared, signaling completion of the process for the current input character. The result is
Finally, the last * is processed. It has higher priority than +, so it is placed on the operator stack. f is then processed and placed on the operand stack, yielding
Since the input is exhausted, the final steps are, for each remaining operator on the operator stack, to pop the operator stack, remove the required number of top operands from the operand stack, apply the operator, and place the result back on top of the operand stack. The final result appears at the top of the operand stack.
The algorithm for the evaluation of any infix expression can now be written. The algorithm, which follows, assumes that a character, when read, will be an entire operand or operator. This means, for example, that ** should be interpreted as a "character." The algorithm returns the value of the expression in evaluate.
1. Initialize the operand stack to empty.
2. Initialize the operator stack to empty.
3. While there is another input character,
read the current character
if the current character is "(", then
push it on the operator stack;
else if the current character is an operand, then
push it on the operand stack;
else if the current character is an operator, then
if the operator stack is not empty, then
if the current character does not have greater priority than the top
operator stack character, then
pop the operator stack, remove the required number of operands
from the operand stack, apply the operator to them, and push the
result on the operand stack
push the current character onto the operator stack
else if the current character is ")", then
pop the operator stack and set topchar to the popped value
while topchar is not (
remove the number of operands required by topchar from the operand
stack, apply topchar to them, and
push the result onto the operand stack
pop the operator stack and set topchar to the popped value
4.While the operator stack is not empty,
pop the operator stack, remove the required number of operands from the
operand stack, apply the operator to them, and push the result on the operand
stack
5.Pop the operand stack and set evaluate to the popped value
Notice that the evaluation of an infix expression requires two stacks rather than the one stack required for the evaluation of a postfix expression. Other operators may be introduced and given appropriate priorities. For example, the assignment operator, =, would be given a higher priority than **.
Suppose, rather than evaluating an infix expression, a programmer wished to translate it and produce the corresponding postfix expression as output. The reason is that postfix expressions can be executed directly, whereas infix expressions are tricky to evaluate. Moreover, if the translation can be done, then the postfix expression may easily be embellished to produce a machine language program for the evaluation of the original infix expression.
The following modification of the infix evaluation algorithm results in such a translation.
1. Eliminate the operand stack. Instead, any pushing onto the operand stack should be changed to outputting the same value.
2. Instead of applying operators to operands, simply output the operators.
The queue, like the stack, is a useful data abstraction for retaining information in a specific order. A queue is a data structure with restricted insertion and deletion operations. Information may be inserted on the queue, but only at the rear end, or bottom. Information may be removed from the queue, but only at the front end, or top.
The queue acts like the pile of Community Chest cards in Monopoly. The top card is the only one that can be removed, and insertions to the pile can be made only at the bottom. If we think of the information stored as representing postponed obligations, then the queue gives access to the obligations in the order in which they were incurred. A popular mnemonic for helping to remember this characteristic is FIFO--first in, first out. Like LIFO, this is a common term in accounting and inventory control systems.
Queues can be implemented in the same basic ways as stacks--as an array of records, as a list with its records stored in an array, and as a list with its records stored in dynamic memory. As in the case of stacks, these implementations are discussed in that order.
A queue may be implemented using an array of records by first declaring
As with stacks, overflow and underflow should be checked in a general implementation. A typical queue situation is depicted in Figure 4.10(a) for the array implementation. Figure 4.10(b) shows the situation after 18, 32, and 15 have been removed and 17 and 20 have been inserted.
Storage for insertion of more records is available at the top of the queuearray, but not at the bottom. To ensure that all the relocated storage for queue is used before overflow occurs, programs "wrap around." That is, the queue is implemented so that the queuearray is viewed as a circle of records, with 0 following the LIMIT, 7. Front is used to point to the entry at the front of the queue, and rear is used to point to the array location in which the next
inserted record is to be placed. As entries are inserted, rear moves down until it "falls off" the array, then it must be "wrapped around." As entries are deleted, front moves down until it "falls off" the array, then it must "wrap around."
The insertion operation may then be implemented as follows:
Setqueue must set front and rear to minus one (-1). Empty will return the value true when front = -1, and false otherwise. The removal of a record can be implemented by a function remove, which returns in value the record that was deleted from the queue.
Now we can turn to implementing a queue as a list with records stored in an array. The availist of Section 3.7 actually acts as a list implementation of a queue if reclaim returns a record to the rear of the availist. Thus queue can be implemented as a list of records stored in an array.
The third queue implementation is also a list--one involving dynamic storage allocation of the records in dynamic memory. First, the following declaration must be made:
Setqueue must set queue to null. Insert will first request storage for the new record to be inserted by invoking malloc. It will then set its info data and insert it as the new last record in the queue. Remove must delete the first record of the queue and return its info data.
Your deck has now been "stacked," you've been "queued" into queues, and you mustn't postpone your obligation to use them!
To bring together the major ideas of this chapter, a case study to check program structure for proper nesting is presented. Its main features are:
1. The top-down approach
2. Demonstration of the use of the stack, treating it as a data abstraction
3. Checking program structure for proper nesting by developing a nonrecursive and a recursive function
4. The different perspectives required to develop the two functions
Every computer programmer has at one time or another gotten error messages saying "incomplete loop structure" or "a missing parenthesis." You now have enough background to write a program that checks for such errors. Let's see how it can be done.
Arithmetic expressions, as well as a program text, consist of sequences of symbols. Complex arithmetic expressions may be composed by properly combining simpler arithmetic expressions, delineated by matching left and right parentheses. The simpler expressions are said to be nested within the more complex expressions that contain them. The complex expression (a * (b + [c /d])) + b) contains two pairs of nested expressions. C programs contain compound statements delimited by matching { (begin) and } (end) pairs. Ignoring all other symbols, these matching pairs must satisfy rules of nesting to be syntactically correct.
Nesting means that one matching pair is wholly contained within another. When pairs are nested, they may not overlap, as do the two pairs in ( [ ) ]. The rules of nesting are the same for any sequence that is built by combining simpler sequences. They require that the start and end of each component be specified. Checking complex sequences to determine that these begin-end pairs do not overlap is an important operation. It provides an interesting application of the stack data abstraction, as well as of recursion. An intimate connection exists among such sequences, stacks, recursions, and trees; it will be explored more fully in later chapters.
Two abstractions of this problem will be considered. The second is a generalization of the first. To begin, assume only one kind of left parenthesis and one kind of matching right parenthesis, and consider sequences composed of these. Thus, at first, expressions such as ([]) are not allowed, since they involve more than one kind of parenthesis.
Given a sequence of left and right parentheses, determine if they may be paired so that they satisfy two conditions:
i. Each pair consists of a left and right parenthesis, with the left parenthesis preceding the right parenthesis.
ii. Each parenthesis occurs in exactly one pair.
If a sequence has a pairing satisfying both of these conditions, the sequence and pairing are valid. The problem is to determine whether a given sequence is valid or not. No sequence starting with a right parenthesis, ")", can be valid, since there is no preceding left parenthesis, "(", to pair with it. Any valid sequence must therefore begin with some series of n "(" parentheses preceding the first appearance of a ")" parenthesis, such as Figure 4.11(a), for which n is 3. Suppose we remove this adjacent pair, the nth "(" parenthesis, and the immediately following first ")" parenthesis. This would be pair 1 in Figure 4.11(a). If the new sequence thus obtained is valid, then adding the removed pair to it results in a valid pairing. Thus the original sequence is valid.
Suppose you find that the resultant sequence is not valid. Can you conclude that the original sequence is not valid? In other words, has constraining one of the pairs to be the first adjacent "(" and ")" parentheses made a pairing of the original sequence satisfying (i) and (ii) impossible? The answer is no. To see this, assume that there is some valid pairing of the original sequence, in which the first ")" parenthesis is not paired with the immediately preceding "(" parenthesis, but there is no valid pairing in which it is. In general, the first ")" parenthesis must then be paired with an earlier "(" parenthesis, and the immediately preceding "("parenthesis must have been paired with a later ")" parenthesis, as in Figure 4.11(b). These two pairs can then be rearranged by interchanging their "(" parentheses. The resultant pairing satisfies conditions (i) and (ii), yet it has the first adjacent "(" parenthesis paired with the immediately following ")" parenthesis, but this is the nesting constraint that has been specified. This contradicts the assumption that no valid pairing satisfies the constraint.
Consequently, the conclusion is that a solution to the problem is obtained as follows:
1. Pair the first adjacent left, "(", and right, ")", parentheses and remove the pair.
2. If the resultant sequence is valid, then so is the original sequence; otherwise the original sequence is not valid.
Think of a left parenthesis as denoting an incurred obligation, and a right parenthesis as the fulfilling of the most recently incurred obligation. This is the precise situation for which a stack is useful. As the program scans a sequence
from left to right, it pushes each "(" parenthesis onto a stack, representing an incurred obligation. Task 1 of the solution may then be carried out by popping the stack when the first ")" parenthesis is encountered, to fulfill the most recently incurred obligation.
Carrying out task 2 requires first determining if the resultant sequence is valid. Notice, however, that had the resultant sequence been processed in this same way, the contents of the stack would be exactly what they are now. Consequently, the program can continue to scan the original sequence (which is exactly what would be seen if it were scanning the resultant sequence), pushing whenever it encounters a "(" parenthesis, and popping whenever it comes to a ")" parenthesis. If the stack is empty when the entire scan is completed, then we have determined that the original sequence is valid; otherwise it is not. During the scan, any attempt to pop an empty stack means that no "(" parenthesis is available to be paired with the ")" parenthesis that caused the attempt (that is, the sequence is invalid).
This solution may be implemented as in the function determine, which follows this paragraph. Note that the stack is treated as a data abstraction . Readchar is a function that reads into its parameter the next character of the input sequence and returns true, unless the character read was a specialchar used as a sentinel, and then it returns false. When determine returns, the entire input sequence has been read. Valid will return true if a pairing satisfying (i) and (ii) exists, and false otherwise.
Nonrecursive Version
Leftparen returns the value true if its parameter is a left parenthesis, and false otherwise. Rightparen is defined similarly. Match returns the value true if topchar and currentchar are left and right parentheses, respectively.
One of the aims of the text is to show how general functions can be adapted to solve particular problems. Determine is such a general function. It can be adapted to evaluate a completely parenthesized infix expression. We repeat the rule of Section 4.6.2 to be used to evaluate such an expression:
1. Scan the infix expression from left to right.
2. When a "matched" pair of "left" and "right" parentheses is encountered,
apply the operator to the operands enclosed within the pair of parentheses, and replace the paired parentheses and the contained operator and operands by the result. Continue scanning from this point.
The matched pairs referred to in this rule are exactly the same as in this case study. Studying the rule, you can see that a right parenthesis signals that an operator and its operands are enclosed between the right parenthesis and its matching left parenthesis.
Determine may be modified to obtain a function evaluate, by defining the process routine as follows:
1. When an operand is encountered, place the operand on top of an operand stack.
2. When an operator is encountered, place the operator on top of the operator stack.
It is also necessary, when a "right" parenthesis is encountered, and the operator stack is not empty, to pop the operator stack, remove the required number of operands from the top of the operand stack, apply the operator to those operands, and place the result on the top of the operand stack. This must be done just before the pop(&s,&topcharacter) statement. Determine's stack, s, plays the role of the operator stack. An operand stack must be introduced and must be available to both the evaluate and process functions.
The general function determine is actually more complex than need be for "paired parentheses." In fact, a stack is not even necessary. All that is really needed is to keep a tally of "(" parentheses, decreasing the tally by 1 every time a ")" parenthesis is read. If the tally ever becomes negative, then determine should, from that point, simply read in the rest of the input sequence and return false. Otherwise, if the tally is zero after the entire input sequence has been read, it should return true. Determine is implemented as shown in the nonrecursive function listed above because it will serve as the solution to the next problem, for which "paired parentheses" will be a special case.
Suppose, instead of containing only "(" and ")" parentheses, the input sequence could consist of any characters. Assume that each character could be either a left or a right character but not both, and also that each left character has a unique right character with which it matches. For instance, a, (, [, and 1 might be "left" characters and the unique "right" characters with which they match z, ), ], and r, respectively.
Given a sequence of left and right characters, determine if they may be paired so that
i. Each pair consists of a left and a right matching character, with the left character preceding the right character.
ii. Each character occurs in exactly one pair.
iii. The sequence of characters between the left and right characters of each pair must also satisfy (i) and (ii).
If a sequence of left and right characters satisfies conditions (i), (ii), and (iii), the sequence and the pairing are valid. Condition (iii) then says that the sequence of characters between the left and right characters of each pair must be valid.
Let's see if this definition makes sense. Consider the above sample "matching" involving a, z, (, ), [, ], l, and r and the sequences of Figure 4.12.
Both the pairings of Figure 4.12(a) and those of Figure 4.12(b) satisfy (i) and (ii). However, only the pairing of (a) satisfies (iii). The pairing of (b) fails because the left and right characters of pair 3 are a and z, and the sequence of characters between them is ])1r. This sequence does not satisfy conditions (i), (ii), and (iii), because none of the six possible ways to form two pairs will be valid. It is also apparent that the pairing of (b) fails, because the left and right characters of pair 2 are "[" and "]" and the sequence of characters between them, a, is not valid. One would have to be sure no other pairings for (b) are valid before concluding that (b)is not a valid sequence.
It is not immediately apparent that this problem generalizes the first problem, even if the characters are restricted to be just left and right parentheses. This is because condition (iii) does not appear in the first problem. However, the reasoning used there shows that adding the condition does not change the problem. In fact, if the left and right matching characters are thought of as different kinds of parentheses, the same reasoning applied in the first problem can be applied to the present problem.
Again, any valid sequence must start with some series of n > 0 left parenthese preceding the first appearance of a right parenthesis. Suppose its matching left parenthesis does not immediately precede it. This is the situation, for example, in Figure 4.12(b), where there are four left parentheses, a, (, [, a, appearing before "]," the first right parenthesis. In order for this first right parenthesis to satisfy (i) and (ii), it must then be paired with a previous matching left parenthesis. But then the immediately preceding left parenthesis is the last character in the sequence between that pair of parentheses. In order to satisfy (iii), this sequence must be valid. This sequence cannot be valid since this last left parenthesis has no matching right parenthesis in this sequence, as indicated in Figure 4.13.
In conclusion, a solution may be obtained as follows:
1. Pair the first adjacent left and right parentheses that match, and remove the pair.
2. If the resultant sequence is valid, then so is the original sequence; otherwise the original sequence is not valid.
Function determine is also an implementation of this solution using a stack, assuming leftparen, rightparen, and match reflect the different left parentheses, right parentheses, and matched pairs, respectively. The stack is needed in order to implement this solution. It is no longer simply a question of increasing or decreasing a tally, depending on whether the program reads a "(" or a ")"parenthesis, and making sure it never goes below zero and ends at zero. It is not even enough to keep a distinct tally for each of the different kinds of "left" and "right" parentheses. This would not result in Figure 4.12(b), for example, being recognized as invalid, because each of the four numbers would satisfy the requirements just mentioned. It is condition (iii), and more than one kind of left and right parentheses, that makes the stack mandatory. Consider a pair satisfying conditions (i) and (ii). To satisfy condition (iii), the sequence of characters between the "left" and "right" parentheses of the pair must also be valid. In effect, a new set of tallies must be kept for that sequence, and they must satisfy the three conditions. The stack is actually holding all of these tallies. Each time a "left" parenthesis appears, it becomes a character in many sequences, in general, and the tally for it, associated with each of those sequences, must be increased by one. Pushing it onto the stack, in effect, increases all these tallies by one simultaneously. Similarly, popping the stack decreases them all simultaneously.
So far the solution has been nonrecursive and has required looking at the input as simply a sequence of parentheses satisfying certain local constraints; a left parenthesis must encounter a matching right parenthesis before any other right parenthesis appears. Any global structure inherent in the input has been ignored. Development of a recursive solution, however, requires that a valid input be defined recursively. The recursive definition of a valid sequence may be restated to show its structure more clearly.
A valid sequence is
A null sequence
A left and right matching pair of parentheses with a valid sequence between them
A valid sequence followed by a valid sequence
In other words, a valid sequence is
A null sequence,
One valid sequence surrounded by a pair of matching parentheses, or
A series of valid sequences, each surrounded by a pair of matching parentheses
The last case would appear as
(valid sequence)(valid sequence) . . . (valid sequence)
The following program is a recursive version of determine based on the recursive definition.
Recursive Version
Determine must be called initially with last set to specialchar. It is used as an input terminator and should not occur in the sequence being checked. When a valid sequence surrounded by a pair of matching parentheses has been encountered, the variable done is set to true. At that point the program continues looking for a next such sequence. However, last must be reinitialized to the specialchar. The variable more is used to signal whether or not more characters remain to be read in the input string. It is declared to be static because it must retain its value between any recursive calls to determine.
Both this recursive solution and the iterative solution work from the inside out. The iterative program looks for adjacent matching left and right parentheses in the interior of the sequence. The recursive program looks for a valid sequence surrounded by a matching pair of parentheses. Thus the iterative solution sees the input
as
and the recursive solution sees it as
where # denotes the specialchar.
Another recursive solution could be written to work from the outside in, looking for a rightmost mate to the first left parenthesis and then checking the sequence between them for validity. This would lead to a less efficient solution, because parentheses could be considered more than once. Recursion often involves this dual possibility, so both should be explored.
1. Set i and j be two integers and define q(i, j) by q(i, j) = 0 if i < j and q(i - j, j) + 1 if i
a. What is the value of q(7,2)?
b. Can we determine q(0,0)?
c. Can we determine q(-3, -4)?
2. Let a be an array of type float and i and n be positive integers. The function
m(a,i,n) is defined by
a. Find m(a,i,n) if i = 1, n = 6, and a is
b. What does m(a,i,n) do?
3. Let a be an array of type real, and i and n be positive integers. The function m(a,i,n) is defined by
a. Find m(a,i,n) for i = 1, n = 6, and a the array of Exercise 2.
b. What does m(a,i,n) do?
4. Let i be a nonnegative integer. Find b(4) where
5. Write a recursive function max corresponding to Exercise 2.
6. Write a recursive function max corresponding to Exercise 3.
7. a. Why does the recursive solution to the Towers of Hanoi problem use the minimum number of moves?
b. What is the number of moves it uses?
8. Consider the following nonrecursive algorithm for the Towers of Hanoi problem.
1. Label the disks 1, 2, . . ., n in increasing order of size.
2. Label the pegs i, a, and
3. Move the smallest disk onto another disk with an even label or onto an empty peg with an even label.
4. If all disks are on the same peg, then terminate. Move the second smallest top disk onto the peg not containing the smallest disk. Go to 1.
a. Convince yourself that this correctly solves the Towers of Hanoi problem.
b. Is the recursive solution or this nonrecursive version easier to understand.
9. Suppose a fourth peg is added to the Towers of Hanoi problem.
a. Write a recursive solution for this problem.
b. Can you find a recursive solution that uses the minimum number of moves for this problem?
10. Mark any n distinct points on the circumference of a circle. How many triangles may be drawn whose vertexes lie on three of the n points?
11. How many ways may k distinct points be selected from the n points of Exercise 10?
12. Given a permutation of 1, 2, . . ., n, let ni be the number of integers to the right of i which exceed i. For the permutation 2134, n1 = 2, n2 = 3, n3 = 1, n4 = 4. Write a process function that will turn permutations into a program that prints n1, n2, . . ., nn for each permutation.
13. Suppose 1 is implemented as a two-way list. Write a recursive function to reverse 1.
14. Implement the function of Exercise 5.
15. Implement the function of Exercise 6.
16. Compare the requirements for the stack storage required during execution for the implementations of Exercises 5 and 6.
17. Why are the more efficient versions of Section 4.4 more efficient?
18. The Fibonacci sequence is defined by
a. Write a recursive function fibonacci(n) to compute and print
b. Analyze its time and storage requirements.
19. a. Translate the program of Exercise 18 and obtain as efficient a version as you can.
b. Analyze its time and storage requirements.
20. Write a nonrecursive program fibonacci(n), which takes O(n) time and uses only four local variables.
21. a. Write a function element with parameter k, which returns the value of the kth element on the stack of integers implemented as in Figure 4.8. For instance, if k is 1, it returns the value of the current first element. It does not disturb the stack at all. Assume you do not have access to the stack directly, but only through the push, pop, and empty routines.
b. Same as Exercise 21(a), except assume you do have direct access to the stack.
22. Two stacks are implemented in one array of length 1,000 as shown. The tops of the stacks are pointed to by top1 and top2 and grow toward each other. Write a procedure push that pushes the contents of v onto the stack indicated by s. s will have a value of 1 or 2. If the stack to which v is to be added is full, then push should not add it, but should return with s set to 0.
23. Write a function maxstack that returns in m the maximal element on a stack of integers implemented with pointer variables. Maxstack will return true when the stack is not empty, and false otherwise.
24 What does the following do?
25. Why are parentheses not needed when prefix or postfix notation is used?
26. How do conventions eliminate ambiguity in infix notation?
27. Evaluate the postfix expression 3 6 + 6 2 / *8+.
28. Simulate the execution of the algorithm of Section 4.6.2 for evaluation of an infix expression on (a * b/(c + d)) + e **
29. Simulate the execution of the translation algorithm of Section 4.6.3 on (a * b/(c + d)) + e **
30. What priority must be given to the assignment operator, =, if the evaluation and translation algorithms for infix to postfix are to work on assignment statements as well as arithmetic expressions?
31. Write the function evaluate.
32. Describe how evaluate must be modified if arithmetic expressions are allowed to include function calls.
33. What will the pairing generated by the function determine be for the input sequence aa([[]()])zz?
34. Modify the function determine so that it outputs the pairs as follows:
35. Modify function determine so that it also outputs ( ( ( ) ) ( ) ), for example, if the input is ( ( ( ) ) ( ) ).
4 2 1 1 2 3 3 4
36. How must determine be modified if some left characters may also be right characters, and they will always match each other? For example, let the left characters be a, (, [,b, with the "right" characters being a, ), ], b. Here a is matched with a, b with b, "("with ")," and "[" with "]." Then a[a] is not valid, but a[CC](aa)a and ab()aab[]a are.
37. Write the remove function for the array implementation of a queue.
38. Write the insert function for the pointer variable implementation of a queue.
39. Write the remove function for the pointer variable implementation of a queue.
40. Suppose function buffer has three parameters, q of type queue, e of type whatever, and op of type character. If op is r, then buffer returns after removing the top record of the queue and copying its value into e. If op is n, then buffer returns after inserting the value in e at the bottom of the queue. Write an implementation of buffer, assuming that access to the queue is only through the empty, remove, and insert routines.
41. A deque (pronounce like "deck") is a data abstraction that retains ordered information, but allows insertion and deletion at both its front and rear.
a. Develop an array-based implementation of a deque and write corresponding setdeque, insertf, insertr, removef, remover, and empty routines.
b. Do the same as in Exercise 41(a), except use pointer variables with dynamic storage allocation for the deque implementation.
42. Suppose there is a program to keep track of the current board configuration in a game of Monopoly by using a circular array of records, each record representing a board position (such as Boardwalk), and queues for Community Chest and Chance. Discuss how the records should be defined, what pointers to records will be convenient, and how these pointers and the circular array should be processed on each turn.
1. Write and simulate a recursive program to reverse a list.
2. You might enjoy finding an algorithm for the following generalization of the Towers of Hanoi problem. The disks are each labelled with a positive integer. A configuration of disks on a peg is "legal" if each disk's integer is no larger than the sum of the integers on all disks below it, or there are no disks below it. How can the disks be moved so that any legal original configuration of n disks on peg 1 ends up on peg 3, with all intermediate configurations being legal?
3. Write the permutation program so it treats the permutation as a data abstraction.
4. In order to use storage efficiently when n stacks are needed during the execution of a program, it may be desirable to implement all the stacks in one array as shown here for n= 4.
The Bi's and Ti's point to the bottoms and tops of the stacks, which grow to the right as indicated. Think of the total storage currently allocated to stack i as being from B(i) to B(i + 1). Stack i is actually using T(i) - B(i + 1) + 1 positions of the array. If B1 = 1, B2 = 10, B3 = 15, B4 = 25, B5 = size of the array = 35, T1 = 3, T2 = 12, T3 = 20, and T4 = 33, then the stacks are using 3, 3, 6, and 9 entries, respectively, while they are allocated 9, 5, 10, and 10 entries.
When an entry is to be inserted into a stack that is currently using all its allocated storage, the stack is said to have overflowed. Stack i overflows if Ti = B(i + 1) - 1. Write a function to manage the storage provided by the array. Whenever a stack overflows, the function is to be invoked. If there is any unused space in the array, then the stack with an unused but allocated position which is "closest" to the overflow stack is to give up one of its unused positions. This position is then used by the overflow stack to accommodate its entry. This function must be written to shift stacks around. If no unused space exists in the array, then the procedure should print an "out of stack storage" message.
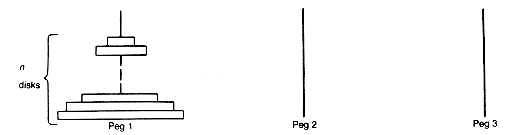
(a) The Initial Problem

(b) After Component 1

(c) After Component 2

(d) After Component 3 -- the Solution!
Figure 4.1 The Towers of Hanoi Problem
To obtain towers(n,i,a,f):
If n = 1, then
move the top disk from peg i to peg f
else
apply towers(n - 1,i,f,a)
moves the top disks from peg i to peg f
apply towers(n - 1,a,i,f).
towers(n,i,a,f)
/* Moves the top n disks from peg i to peg f
*/
int n,i,a,f;
{if(n == 1)
printf("\n %d -> %d\n",i,f);else
{towers(n-1,i,f,a);
printf("\n %d -> %d\n",i,f);towers(n-1,a,i,f);
}
}
4.2.2 Verifying and Simulating a Recursive Program
towers(3,1,3,2)
printf("\n %d -> %d\n",1,3);towers(3,2,1,3)
 3 is to be output. (1
3 is to be output. (1  3 means "Move the top disk from peg 1 to peg 3.") Then another recursive call must be simulated, towers(3,2,1,3).
3 means "Move the top disk from peg 1 to peg 3.") Then another recursive call must be simulated, towers(3,2,1,3).towers(2,1,2,3)
printf("\n %d -> %d\n",1,2);towers(2,3,1,2)
 2 is to be output, and then another recursive call must be simulated: towers(2,3,1,2).
2 is to be output, and then another recursive call must be simulated: towers(2,3,1,2).towers(1,1,3,2)
printf("\n %d -> %d\n",1,3);towers(1,2,1,3)
 2, 1
2, 1 3, and 2
3, and 2  3, respectively. This completes the second recursive call (towers(2,1,2,3)) so we must pick up the simulation at the proper point, which is to output l
3, respectively. This completes the second recursive call (towers(2,1,2,3)) so we must pick up the simulation at the proper point, which is to output l  2 and then make the fifth recursive call to simulate towers(2,3,1,2).
2 and then make the fifth recursive call to simulate towers(2,3,1,2).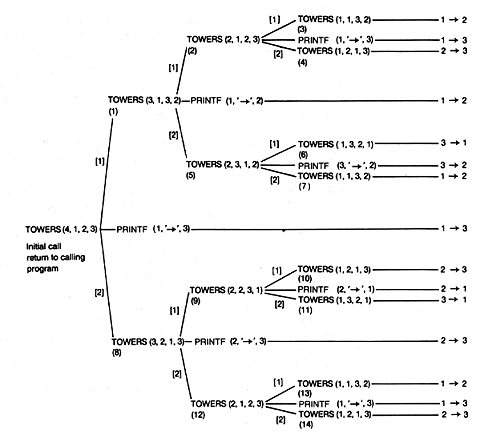
Figure 4.2 Bookkeeping for the Simulation of a Recursive Program
 2 means, "move the top disk from peg l to peg 2." The solution is the same as our earlier one.
2 means, "move the top disk from peg l to peg 2." The solution is the same as our earlier one.To obtain towers(n,i,a,f):
If n = 1, then
move the top disk from i to f
else
apply towers (n - 1,i,f,a)
move the top disk from i to f
apply towers(n - 1,a,i,f).
4.2.3 The Length of a List
length(listname)
/* Returns the number of records
in the list pointed to by listname.
*/
listpointer listname;
{listpointer setnull(),next();
if(listname == setnull())
return(0);
else
return(1 + length(next(listname)));
}
4.2.4 Copying a List
copy(first,psecond)
/* Creates a new list which is a copy
of the list pointed to by first and
whose head is second
*/
listpointer first,*psecond;
{listpointer null, rest,setnull(),avail(),next();
null = setnull();
if(first == null)
*psecond = null;
else
{*psecond = avail();
setinfo(*psecond,first);
copy(next(first),&rest);
setlink(*psecond,rest);
}
}
4.2.5 Local and Global Variables and Parameters
simple (x,py)
int x, *py;
{x = 1;
*py = 2;
*py = x + *py;
}
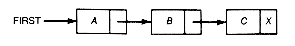
Figure 4.3 The List for COPY to Process

(a) The Situation after SETINF0 (*PSECOND, FIRST0)

(b) After SETINF0(REST1, FIRST1)

(c) After SETINF0(REST2, FIRST 2)

(d) After REST2:= NULL 3; i.e., SECOND:= NULL

(e) After SETLINK(REST1, REST2)
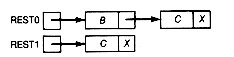
(f) After SETLINK(REST0, REST1)
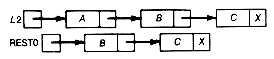
Figure 4.4 Simulation of COPY(FIRST,&SECOND)
listpointer copy(first)
/* Returns a pointer to the first record of a new list which is a
copy of the list first.
*/
listpointer first;
{listpointer null,second,setnull(),avail(),next();
null = setnull();
if (first == null)
second = null;
else
{second = avail();
setinfo(second,first);
setlink(second,copy(next(first)));
}
return (second);
}
4.2.6 Counting Squares
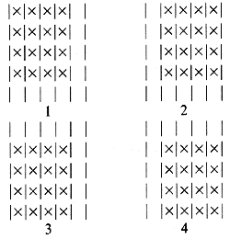
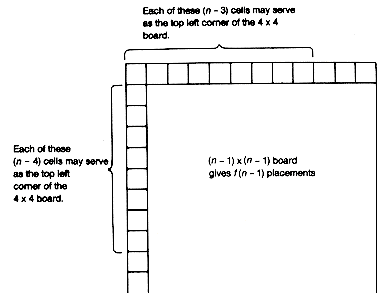
Figure 4.5 An n x n Checkerboard
 5. If n = 4, f(4) = 1. So the following is true.
5. If n = 4, f(4) = 1. So the following is true.f(n) is
1 if n = 4
f(n - 1) + (n - 3) + (n - 4) if n
 5
5 4.
4.f(n)
int n;
{if (n == 4)
return (1);
else
return(f(n-1)+(n-3)+(n-4));
}
f(7) = f(6) + (7 - 3) + (7 - 4)
f(6) = f(5) + (6 - 3) + (6 - 4)
f(5) = f(4) + (5 - 3) + (5 - 4)
f(4) = 1
f(5) = 1 + 2 + 1 = 4
f(6) = 4 + 3 + 2 = 9
f(7) = 9 + 4 + 3 = 16
 4. The program for this solution would be
4. The program for this solution would bef(n)
int n;
{return((n-3)*(n-3));
}
4.2.7 Permutations
permutations(n)
/* Generates and processes each
permutation of the integers
1 to n.
*/
int n;
{int done;
done = FALSE;
initialize(n);
while (!done)
{process(n);
next(n,&done);
}
}
4 3 2 1
3 4 2 1
3 2 4 1
3 2 1 4
4 2 3 1
2 4 3 1
2 3 4 1
2 3 1 4
4 2 1 3
2 4 1 3
2 1 4 3
2 1 3 4
4 3 1 2 4 1 3 2 4 1 2 3
3 4 1 2 1 4 3 2 1 4 2 3
3 1 4 2 1 3 4 2 1 2 4 3
3 1 2 4 1 3 2 4 and 1 2 3 4
next (n,pdone)
If n is not 1, then
If n is not at the right end of the current permutation of 1, . . , n then
shift it right one position
else
remove "n" from the current permutation of 1, . . , n
next(n - 1,pdone)
Insert "n" at the left end of the current permutation of 1, . . , n - 1
else
set done to true.
 i
i  n. Next may be defined as
n. Next may be defined asnext(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone;
{int i;
if (n > 1)
if (l[n] < n)
{p[l[n]] = p[l[n]+1];
p[l[n]+1] = n;
l[n] = l[n]+1;
}
else
{next(n-1,pdone);
for (i=n-1;i>=1;i--)
p[i+1] = p[i];
p[1] = n;
l[n] = 1;
}
else
*pdone = TRUE;
}
 k
k  n. Now next may be defined as follows:
n. Now next may be defined as follows:next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone;
{if (n > 1)
if (ptr[n]->link != NULL)
{pred[n]->link = ptr[n]->link;
pred[n] = pred[n]->link;
ptr[n]->link = pred[n]->link;
pred[n]->link = ptr[n];
}
else
{pred[n]->link = NULL;
next(n-l,pdone);
ptr[n]->link = p->link;
p->link = ptr[n];
pred[n] = p;
}
else
*pdone = TRUE;
}
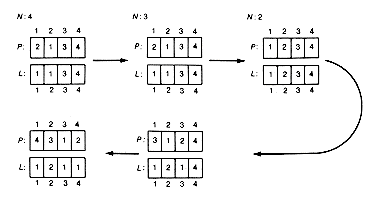
(a) Array Implementation for P
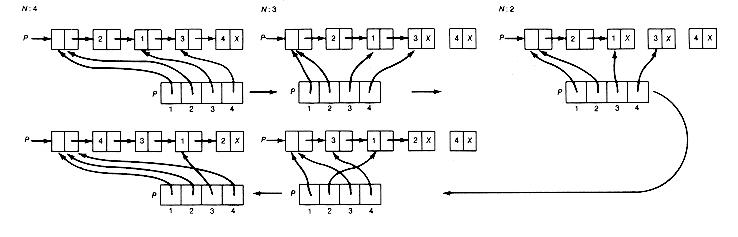
(b) List Implementation for P
Figure 4.6 Simulation of NEXT (4,&DONE) When P is 2134
#include <stdio.h>
#define TRUE 1
#define FALSE 0
typedef int arraytype[21];
arraytype p,l;
main()
/* Driver for permutations. */
{int n;
printf("\n n = ?\n");scanf("%d",&n);permutations(n);
}
permutations(n)
/* Generates and processes each
permutation of the integers
1 to n.
*/
int n;
{int done;
done = FALSE;
initialize(n);
while (!done)
{process(n);
next(n,&done);
}
}
initialize(n)
/* Creates initial permutation */
int n;
{int i;
for (i = 1;i<=n;i++)
{p[i] = n - i + 1;
l[i] = 1;
}
}
process(n)
/* Prints the current permutation */
int n;
{int i;
for (i=1;i<=n;i++)
printf("\n%d\n",p[i]);printf("\n");}
next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone;
{int i;
if (n > 1)
if (l[n] < n)
{p[l[n]] = p[l[n]1];
p[l[n]+1] = n;
l[n] = l[n]+1;
}
else
{next(n-1,pdone);
for (i=n-1;i>=1;i--)
p[i+1] = p[i];
p[1] = n;
l[n] = 1;
}
else
*pdone = TRUE;
}
#include <stdio.h>
#define TRUE l
#define FALSE 0
#define NULL 0
typedef struct record
{int info;
struct record *link;
}listrecord,*listpointer;
typedef listpointer pointerarray[21];
pointerarray ptr,pred;
listpointer p;
main()
/* Driver for permutations. */
{int n;
printf("\n n = ?\n");scanf("%d",&n);permutations(n);
}
permutations(n)
/* Generates and processes each
permutation of the integers 1 to n.
*/
int n;
{int done;
done = FALSE;
initialize(n);
while (!done)
{process(n);
next(n,&done);
}
}
initialize(n)
/* Creates initial permutation */
int n;
{int i;
listpointer q;
p = malloc(sizeof(listrecord));
q = P;
for (i=1;i<=n;i++)
{q->link = malloc(sizeof(listrecord));
q = q->link;
q->info = n - i + 1;
ptr[n-i+1] = q;
pred[i] = p;
}
q->link = NULL;
}
process(n)
/* Prints the current permutation */
int n;
{listpointer q;
q = p->link;
while (q != NULL)
{printf("\n%d\n",q->info);q = q->link;
}
printf("\n");}
next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone;
{if (n > 1)
if (ptr[n]->link != NULL)
{pred[n]->link = ptr[n]->link;
pred[n] = pred[n]->link;
ptr[n]->link = pred[n]->link;
pred[n]->link = ptr[n];
}
else
{pred[n]->link = NULL;
next(n-1,pdone);
ptr[n]->link = p->link;
p->link = ptr[n];
pred[n] = p;
}
else
*pdone = TRUE;
}
4.3: A Close Look at the Execution of Recursive Programs
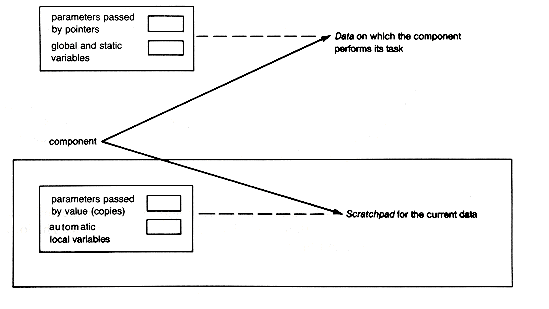
Figure 4.7 Data and Scratchpad for a Component
[2] and n = 4, i = l, a = 2, f = 3 for the initial call
[1] and n = 3, i = 2, a = 1, f = 3 for the eighth recursive call
[1] and n = 2, i = 2, a = 3, f = 1 for the ninth recursive call
first0, null0, rest0 for the initial call
first1, null1, rest1 for the first recursive call
first2, null2, rest2 for the second recursive call
n = 4 for the initial call
n = 3 for the second recursive call
n = 2 for the third recursive call
4.4: Implementing Recursive Programs
4.4.1 A Sample Implementation of Towers
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{if(n == 1)
printf("\n %d -> %d\n",i,f);else
{towers(n-1,i,f,a);
printf("\n %d -> %d\n",i,f)towers(n-1,a,i,f);
}
}
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{int retrn;
stack s;
setstack(&s);
one: if(n == 1)
printf("\n %d -> %d\n",i,f);else
{s_tack(1,n,i,a,f &s);
setvar1(&n,&i,&a,&f);
goto one;
}
two: if(!empty(&s))
{restore(&retrn,&n,&i,&a,&f,&s);
switch(retrn)
{case 1:
printf("\n %d -> %d\n",i,f)
s_tack(2,n,i,a,f,&s);
setvar2(&n,&i,&a,&f);
goto one;
case 2:
goto two;
}
}
}
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{stack s;
setstack(&s);
one: if(n == 1)
printf("\n %d -> %d\n",i,f);else
{s_tack(n,i,a,f,&s);
setvar1(&n,&i,&a,&f);
goto one;
}
if(!empty(&s))
{restore(&n,&i,&a,&f,&s);
printf("\n %d -> %d\n",i,f);setvar2(&n,&i,&a,&f);
goto one;
}
}
one: if(n == 1) one: while(n > 1)
printf("\n %d -> %d\n",i,f); {else s_tack(n,i,a,f,&s);
{ setvar1(&n,&i,&a,&f);s_tack(n,i,a,f,&s); }
setvar1(&n,&i,&a,&f); printf("\n %d -> %d\n",i,f);goto one;
}
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{stack s;
one: while(n > 1)
{s_tack(n,i,a,f,&s);
setvar1(&n,&i,&a,&f);
}
printf("\n %d -> %d\n",i,f);if(!empty(&s))
{restore(&n,&i,&a,&f,&s);
printf("\n %d -> %d\n",i,f);setvar2(&n,&i,&a,&f);
goto one;
}
}
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{stack s;
int done
done = FALSE;
while(!done)
{while(n > 1)
{s_tack(n,i,a,f,&s);
setvar1(&n,&i,&a,&f);
}
printf("\n %d -> %d\n",i,f);if(!empty(&s))
{restore(&n,&i,&a,&f,&s);
printf("\n %d -> %d\n",i,f);setvar2(&n,&i,&a,&f);
}
else
done = TRUE;
}
4.4.2 A Sample Implementation for Permutations
next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone;
{int i,retrn;
stack s;
one: if(n > 1)
if(l[n] < n)
{p[l[n]] = p[l[n] + 1];
p[l[n] + 1] = n;
l[n] = l[n] + 1;
}
else
{s_tack(1,n,i,&s);
setvar(&n,&i);
goto one;
}
else
*pdone = TRUE;
two: if(!empty(&s))
{restore(&retrn,&n,&i,&s);
switch(retrn)
{case 1:
{for(i=n-1;i>=1;i--)
p[i+1] = p[i];
p[1] = n;
l[n] = 1;
goto two;
{{{{one: if c1 then
if c2 then
task c1 and c2 both true
else
task for c1 true but c2 false
goto one
else
task for c1 false
while not empty(&s)
loop task
while (c1 and not c2)
task for c1 true but c2 false
if c1, then
task for c1 and c2 both true
else
task for c1 false
while not empty (&s)
loop task.
next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone
{int i,retrn;
stack s;
while((n > 1) && !(l[n] < n))
{s_tack(1,n,i,&s);
setvar(&n,&i);
}
if(n > 1)
{p[l[n]] = p[l[n] + 1];
p[l[n] + 1] = n;
l[n] = l[n] + 1;
}
else
*pdone = TRUE;
while(!empty(&s))
{restore(&retrn,&n,&i,&s);
switch(retrn)
{case 1:
{for(i=n-1;i>=1;i--)
p[i+1] = p[i];
p[1] = n;
l[n] = 1;
}
}
}
}
next(n,pdone)
/* Generates the next permutation unless
the current one is the last. In this case
done is set to true.
*/
int n,*pdone
{int i,s;
1. s = n;
2. while((n > 1) && !(l[n] < n))
n--;
3. if(n > 1)
{p[l[n]] = p[l[n] + 1];
p[l[n] + 1] = n;
l[n] = l[n] + 1;
}
else
*pdone = TRUE;
4. while(s > n)
{n++
for(i=n-1;i>=1;i--)
p[i+1] = p[i];
p[1] = n;
l[n] = 1;
}
}
4.5: Stacks
4.5.1 Array Implementation of a Stack
typedef struct
{whatever info;
}stackrecord;
typedef struct
{stackrecord stackarray [LIMIT];
int top;
}stack;
stack s;
pop(&s,&y);
pop(&s,&z);
push(&newrecord,&s);
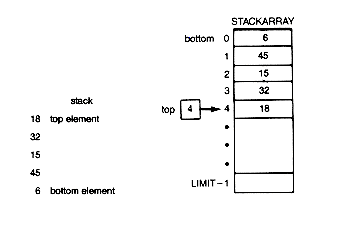
(a) The Stack Data Abstraction
(b) Array Implementation of the Stack
Figure 4.8 Stack before Insertion of a New Element
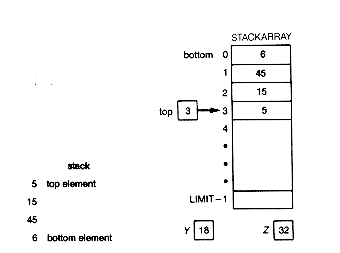
(a) The Stack Data Abstraction
(b) Array Implementation of the Stack
Figure 4.9 Stack after Insertion of a New Element
setstack (ps)
/* Initializes the stack s to empty */
stack *ps;
{(*ps).top = -1;
}
empty (ps)
/* Returns true only if the stack is empty */
stack *ps;
{return ((*ps).top == -1);
}
push (pnewrecord,ps)
/* Inserts the record newrecord
at the top of the stack s
*/
stackrecord *pnewrecord,
stack *ps;
{if ((*ps).top == (LIMIT - 1))
overflow(ps);
else
{(*ps).top = (*ps).top + 1;
(*ps).stackarray[(*ps).top].info =
(*pnewrecord).info;
}
}
pop(ps,pvalue)
/* Copies the contents of the top record
of stack s into value and removes the
record from the stack
*/
stack *ps;
stackrecord *pvalue;
{if(empty(ps))
underflow(ps);
else
{(*pvalue).info = (*ps).stackarray
[(*ps).top].info;
(*ps).top = (*ps).top - 1;
}
}
(*ps).stackarray[(*ps).top].info =
(*pnewrecord).info;
typedef struct
{whatever stackarray [LIMIT];
int top;
}stack;
push(value,ps)
/* Inserts the new value
at the top of the stack s
*/
whatever value;
stack *ps;
{if((*ps).top == (LIMIT-1))
overflow(ps);
else
{(*ps).top = (*ps).top + 1;
(*ps).stackarray[(*ps).top] = value;
}
}
pop(ps,pvalue)
/* Copies the contents of the top entry
of stack s into value and removes it
from the stack
*/
stack *ps;
whatever *pvalue;
{if(empty(ps))
underflow(ps);
else
{*pvalue = (*ps).stackarray[(*ps).top];
(*ps).top = (*ps).top - 1;
}
}
#include <stdio.h>
#define LIMIT 50
typedef struct
{int n;
int i;
int a;
int f;
}whatever;
typedef struct
{whatever info;
}stackrecord;
typedef struct
{stackrecord stackarray [LIMIT];
int top;
}stack;
setstack(ps)
/* Initializes the stack s to empty */
stack *ps;
{(*ps).top = -1;
}
empty(ps)
/* Returns true only if the stack s is empty */
stack *ps;
{return((*ps).top == -1);
}
push(pnewrecord,ps)
/* Inserts the record newrecord
at the top of the stack s
*/
stackrecord *pnewrecord;
stack *ps;
{if ((*ps).top == (LIMIT-1))
overflow(ps);
else
{(*ps).top = (*ps).top + 1;
(*ps).stackarray[(*ps).top].info =
(*pnewrecord).info;
}
}
pop(ps,pvalue)
/* Copies the contents of the top record
of stack s into value and removes the
record from the stack
*/
stack *ps;
stackrecord *pvalue;
{if (empty(ps))
underflow(ps);
else
{(*pvalue).info =
(*ps).stackarray[(*ps).top].info;
(*ps).top = (*ps).top - 1;
}
}
overflow(ps);
/* Prints a message that the stack has overflowed */
stack *ps;
{printf(" The stack has overflowed \n");}
underflow(ps);
/* Prints a message that the stack has underflowed */
stack *ps;
{printf(" The stack has underflowed \n");}
main()
/* Driver for towers */
{int n;
printf("\n enter a value for n\n");scanf("%d",&n);towers(n,1,2,3);
}
towers(n,i,a,f)
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{stack s;
int done;
setstack(&s);
done = FALSE;
while(!done)
{while (n > 1)
{s_tack(n,i,a,f,&s);
setvar1(&n,&i,&a,&f);
}
printf("\n %d -> %d\n",i,f);if(!empty(&s))
{restore(&n,&i,&a,&f,&s);
printf("\n %d -> %d\n",i,f);setvar2(&n,&i,&a,&f);
}
else
done = TRUE;
}
setvar1(pn,pi,pa,pf)
/* Sets n to n-1 and
interchanges f and a
*/
int *pn,*pi,*pa,*pf;
{int t;
*pn = *pn-1;
t = *pf;
*pf = *pa;
*pa = t;
}
setvar2(pn,pi,pa,pf)
/* Sets n to n-1 and interchanges a and i
*/
int *pn,*pi,*pa,*pf;
{int t;
*pn = *pn-1;
t = *pa;
*pa = *pi;
*pi = t;
}
s_tack(n,i,a,f,ps)
/* Creates a record containing
n,i,a, and f and inserts it
on stack s
*/
int n,i,a,f;
stack *ps;
{stackrecord newrecord;
newrecord.info.n = n;
newrecord.info.i = i;
newrecord.info.a = a;
newrecord.info.f= f;
push(&newrecord,ps);
}
restore(pn,pi,pa,pf,ps)
/* Removes the top record from
stack s and copies its contents
into n,i,a,f
*/
int *pn,*pi,*pa,*pf;
stack *ps;
{stackrecord value;
pop(ps,&value);
*pn = value.info.n;
*pi = value.info.i;
*pa = value.info.a;
*pf = value.info.f;
}
4.5.2 List Implementation of the Stack with an Array of Records
4.5.3 List Implementation of the Stack with Records in Dynamic Memory
typedef struct record
{struct whatever info;
struct record *link;
}stackrecord,*stack;
setstack(ps)
/* Initializes the stack s to empty */
stack *ps;
{*ps = NULL;
}
empty(ps)
/* Returns true only if the stack s is empty */
stack *ps;
{return(*ps == NULL);
}
push(pnewrecord,ps)
/* Inserts the record newrecord
at the top of the stack s
*/
stackrecord *pnewrecord;
stack *ps;
{stackrecord *newentry;
newentry = malloc(sizeof(stackrecord));
newentry->info = pnewrecord->info;
newentry->link = *ps;
*ps = newentry;
}
pop(ps,pvalue)
/* Copies the contents of the top record
of stack s into value and removes the
record from the stack
*/
stack *ps;
stackrecord *pvalue;
{if(!empty(ps))
{pvalue->info = (*ps)->info;
*ps = (*ps)->link;
}
else
underflow(ps);
}
#include <stdio.h>
#define NULL 0
typedef struct
{int n;
int i;
int a;
int f;
}whatever;
typedef struct record
{whatever info;
struct record *link;
}stackrecord, *stack;
setstack(ps)
/* Initializes the stack s to empty */
stack *ps;
{*ps = NULL;
}
empty(ps)
stack *ps;
{return(*ps == NULL);
}
push(pnewrecord,ps)
stackrecord *pnewrecord;
stack *ps;
{stackrecord *newentry;
newentry = malloc(sizeof(stackrecord));
newentry->info = pnewrecord->info;
newentry->link = *ps;
*ps = newentry;
}
pop(ps,pvalue)
/* Copies the contents of the top record
of stack s into value and removes the
record from the stack
*/
stack *ps;
stackrecord *pvalue;
{if(!empty(ps))
{pvalue->info = (*ps)->info;
*ps = (*ps)->link;
}
else
underflow(ps);
}
overflow(ps);
/* Prints a message that the stack has overflowed */
stack *ps;
{printf(" The stack has overflowed \n");}
underflow(ps);
/* Prints a message that the stack has underflowed */
stack *ps;
{printf(" The stack has underflowed \n");}
main()
/* Driver for towers */
{int n;
printf("\n enter a value for n \n");scanf("%d",&n);towers(n,1,2,3);
}
towers(n,i,a,f)
1 final nonrecursive version
/* Moves the top n disks
from peg i to peg f
*/
int n,i,a,f;
{stack s;
1 allocates storage for s (an instance of type stack)
int done
setstack(&s);
done = FALSE;
while(!done)
{while (n > 1)
{s_tack(n,i,a,f,&s);
setvar 1(&n,&i,&a,&f);
}
printf("\n %d -> %d\n",i,f);if(!empty(&s))
{restore(&n,&i,&a,&f,&s);
printf("\n %d -> %d\n",i,f);setvar2(&n,&i,&a,&f);
}
else
done = TRUE;
}
setvar1(pn,pi,pa,pf)
/* Sets n to n - 1 and
interchanges f and a
*/
int *pn,*pi,*pa,*pf;
{int t;
*pn = *pn - 1;
t = *pf;
*pf = *pa;
*pa = t;
}
setvar2(pn,pi,pa,pf)
/* Sets n to n - 1 and
interchanges a and i
*/
int *pn,*pi,*pa,*pf;
{int t;
*pn = *pn - 1;
t = *pa;
*pa = *pi;
*pi = t;
}
s_tack(n,i,a,f,ps)
/* Creates a record containing
n, i, a, and f and inserts it
on stack s
*/
int n,i,a,f;
stack *ps;
{stackrecord newrecord;
newrecord.info.n = n;
newrecord.info.i = i;
newrecord.info.a = a;
newrecord.info.f = f;
push(&newrecord,ps);
}
restore(pn,pi,pa,pf,ps)
/* Removes the top record from
stack s and copies its contents
into n,i,a,f
*/
int *pn,*pi,*pa,*pf;
stack *ps;
{stackrecord value;
pop(ps,&value);
*pn = value.info.n;
*pi = value.info.i;
*pa = value.info.a
*pf = value.info.f;
}
4.6: Evaluation and Translation of Expressions
Table 4.1 Notations for Two
Arithmetic Expressions
a + (b * c) (a + b) * c
Prefix + a * bc * + abc
Infix a + b * c a + b * c
Postfix abc * + ab + c *
4.6.1 Postfix Expressions
((a + b) * (c/d))
a + b * c/d
((a + b) * (c/d))
(((a + b) * c)/d)
((a + (b * c))/d)
(a + ((b * c)/d))
(a + (b * (c/d)))
ab + cd/*
((a + b) * (c/d))
((a + b) * (c/d)) .... ab + cd/*
(((a + b) * c)/d) .... ab + c * d/
((a + (b * c))/d) .... abc* + d/
(a + ((b * c)/d)) .... abc*d/+
(a + (b * (c/d))) .... abcd/*+
Table 4.2 Evaluation of a Postfix Expression
Input Operand Stack
a a
b b
a
c c
b
a
* (b * c)
a
d d
(b * c)
a
/ ((b * c)/d)
a
+ (a + ((b * c)/d)
4.6.2 Infix Expressions
a + b * c/d
Operand Stack Operator Stack
--------------------------------
b +
a
(a + b) * c/d
a + (b * c/d ** e) *f
Operand Stack Operator Stack
--------------------------------
b (
a +
Operand Stack Operator Stack
---------------------------------
c *
b (
a +
Operand Stack Operator Stack
---------------------------------
d /
(b * c) (
a +
Operand Stack Operator Stack
---------------------------------
e **
d /
(b * c) (
a +
Operand Stack Operator Stack
----------------------------------
((b * c)/(d ** e)) +
a
Operand Stack Operator Stack
-----------------------------------
f *
((b * c)/(d ** e)) +
a
4.6.3 Translating Infix to Postfix
4.7: Queues
4.7.1 Array and Circular Array Implementation of the Queue
typedef struct
{whatever info;
}queuerecord;
typedef struct
{queuerecord queuearray [LIMIT];
int front, rear;
}queue;
queue q;
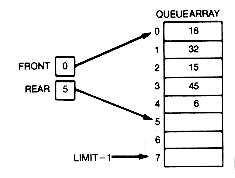
(a) Initial Configuration
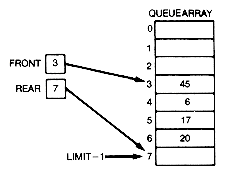
(b) After Three Records Are Removed and Two Records Are Inserted
Figure 4.10 Typical Queue Configuration for an Array Implementation
insert(pnewrecord,pq)
/* Inserts newrecord at the rear of queue q */
queuerecord *pnewrecord;
queue *pq;
{if ((*pq).front == -1)
{(*pq).front = 0;
(*pq).queuearray[0].info = (*pnewrecord).info;
(*pq).rear = 1;
}
else
if((*pq).rear == (*pq).front)
printf("\n overflow \n");else
{if((*pq).rear <= (LIMIT - 1))
{(*pq).queuearray[(*pq).rear].info =
(*pnewrecord).info;
(*pq).rear = (*pq).rear + 1;
}
else
{if((*pq).front == 0)
printf("\n overflow \n");else
{4 there is room to wrap around, so the new entry is inserted at the start of the array and rear set to the next location
(*pq).queuearray[0].info =
(*pnewrecord).info;
(*pq).rear = 1;
}
}
}
}
remove (pq, pvalue)
/* Deletes the front entry from
queue q and copies its contents
into value
*/
queue *pq;
queuerecord *pvalue;
{if(empty(pq))
printf("\n underflow \n");else
{(*pvalue).info = (*pq).queuearray
[(*pq).front].info;
(*pq).front = (*pq).front + 1;
if((*pq).front == (*pq).rear)
2 if queue is empty, then reinitialize it
setqueue(pq);
if((*pq).front > (LIMIT - 1))
(*pq).front = 0;
}
}
4.7.2 List Implementation of the Queue with an Array of Records
4.7.3 List Implementation of the Queue with Records in Dynamic Memory
typedef struct record
{whatever info;
struct record *link;
}queuerecord,*queue;
4.8: Case Study: Checking Sequences for Proper Nesting
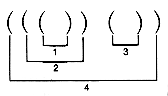
(a) Four Pairs Satisfying Conditions i and ii
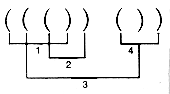
(b) Four Other Pairs Satisfying Conditions i and ii

(c) Four Pairs Not Satisfying Conditions i and ii; No Other Four Pairs Will
Figure 4.11 Valid and Invalid Nesting of Parentheses
determine(pvalid)
/* Returns true in valid only if the
input sequence is properly nested
*/
int *pvalid;
{char currentchar;
struct
{char topchar;
}topcharacter;
stack s;
*pvalid = TRUE;
setstack(&s);
while(readchar(¤tchar))
if(leftparen(currentchar))
push(¤tchar,&s);
else if(rightparen(currentchar))
if(!empty(&s))
{pop(&s,&topcharacter);
if(!match(topcharacter.topchar,
currentchar))
*pvalid = FALSE;
}
else
*pvalid = FALSE;
else
process(currentchar,&s);
if(!empty(&s))
*pvalid = FALSE;
}
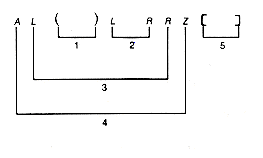
(a) Five pairs Satisfying Conditions i-iii
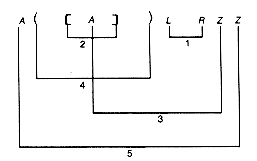
(b) Five Pairs Not Satisfying Conditions i-iii; No Other Five Pairs Will
Figure 4.12 Valid and Invalid Nesting of Matched Characters
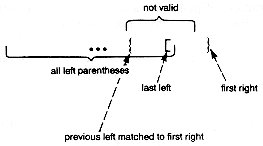
Figure 4.13 An Invalid Nesting Sequence
determine(pvalid,last)
/* Returns true in valid only if the input
sequence is properly nested; last must
initially contain a special character
used as the input terminator.
*/
int *pvalid;
char last;
{char currentchar;
int done;
static int more;
done = FALSE;
more = TRUE;
while(!done && more)
17 loops through each input character
{more = readchar(¤tchar);
if(leftparen(currentchar))
determine(pvalid,currentchar);
else if(rightparen(currentchar))
if(!match (last,currentchar))
*pvalid = FALSE;
else
{done = TRUE;
last = SPECIALCHAR;
}
else
process(last,currentchar);
}
if(last != SPECIALCHAR)
*pvalid = FALSE;
}
[ ( [ ] ) ] ( ) { [ ] } #[ ( [ 1 ] ) ] ( 4 ) { [ 5 ] } # (6 pairs of matching parentheses)- 2 - - 6 -
- - 3 - -
[ ( [ ] ) ] ( 2 ) { [ ] } # (3 valid sequences each one surrounded by a pair of- - 1 - - - 3 - matching parentheses)
Exercises
 j
jm(a,i,n) = a[i] if i = n and max(m(a,i + 1,n) ,a[i]) if i < n
0. 6.8
1. 3.2
2. -5.0
3. 14.6
4. 7.8
5. 9.6
6. 3.2
7. 4.0

 (i + n)/2
(i + n)/2 means, "Do an integer divide of (i + n)/2."
means, "Do an integer divide of (i + n)/2."b(0) = 1
b(n) = b(0) X b(n - 1) + b(1) X b(n - 2)
+ b(2) X b(n - 3) + . . . + b(n - 1) X b(0) n>0
 , respectively, n + 1, n + 2, and n + 3.
, respectively, n + 1, n + 2, and n + 3. (0) = 0,
(0) = 0,  (1) = 1
(1) = 1 (n) = f(n - 1) +
(n) = f(n - 1) +  (n - 2) for n = 2,3,4 . . .
(n - 2) for n = 2,3,4 . . . (n).
(n).
pop(&s,&value);
push(&value,&s)
 .
. .
.1 2 3 4 5 6 7 8
if ( ( ( ) ) ( ) ) is the input sequence,
then the output will be the pairs 3 4, 2 5, 6 7, 1 8.
Suggested Assignments



