This chapter discusses three of the most simple and basic data structures. Virtually every significant program will use at least one of these structures explicitly, and a stack is always implicitly used in your program, whether or not you declare one. Among the highlights of this chapter, we will
Introduce the concept of Abstract Data Types (ADTs).
Show how to efficiently perform operations on lists.
Introduce the stack ADT and its use in implementing recursion.
Introduce the queue ADT and its use in operating systems and algorithm design.
Because these data structures are so important, one might expect that they are hard to implement. In fact, they are extremely easy to code up; the main difficulty is keeping enough discipline to write good general-purpose code for routines that are generally only a few lines long.
One of the basic rules concerning programming is that no routine should ever exceed a page. This is accomplished by breaking the program down into modules. Each module is a logical unit and does a specific job. Its size is kept small by calling other modules. Modularity has several advantages. First, it is much easier to debug small routines than large routines. Second, it is easier for several people to work on a modular program simultaneously. Third, a well-written modular program places certain dependencies in only one routine, making changes easier. For instance, if output needs to be written in a certain format, it is certainly important to have one routine to do this. If printing statements are scattered throughout the program, it will take considerably longer to make modifications. The idea that global variables and side effects are bad is directly attributable to the idea that modularity is good.
An abstract data type (ADT) is a set of operations. Abstract data types are mathematical abstractions; nowhere in an ADT's definition is there any mention of how the set of operations is implemented. This can be viewed as an extension of modular design.
Objects such as lists, sets, and graphs, along with their operations, can be viewed as abstract data types, just as integers, reals, and booleans are data types. Integers, reals, and booleans have operations associated with them, and so do abstract data types. For the set ADT, we might have such operations as union, intersection, size, and complement. Alternately, we might only want the two operations union and find, which would define a different ADT on the set.
The basic idea is that the implementation of these operations is written once in the program, and any other part of the program that needs to perform an operation on the ADT can do so by calling the appropriate function. If for some reason implementation details need to change, it should be easy to do so by merely changing the routines that perform the ADT operations. This change, in a perfect world, would be completely transparent to the rest of the program.
There is no rule telling us which operations must be supported for each ADT; this is a design decision. Error handling and tie breaking (where appropriate) are also generally up to the program designer. The three data structures that we will study in this chapter are primary examples of ADTs. We will see how each can be implemented in several ways, but if they are done correctly, the programs that use them will not need to know which implementation was used.
We will deal with a general list of the form a1, a2, a3, . . . , an. We say that the size of this list is n. We will call the special list of size 0 a null list.
For any list except the null list, we say that ai+l follows (or succeeds) ai (i < n) and that ai-1 precedes ai (i > 1). The first element of the list is a1, and the last element is an. We will not define the predecessor of a1 or the successor of an. The position of element ai in a list is i. Throughout this discussion, we will assume, to simplify matters, that the elements in the list are integers, but in general, arbitrarily complex elements are allowed.
Associated with these "definitions" is a set of operations that we would like to perform on the list ADT. Some popular operations are print_list and make_null, which do the obvious things; find, which returns the position of the first occurrence of a key; insert and delete, which generally insert and delete some key from some position in the list; and find_kth, which returns the element in some position (specified as an argument). If the list is 34, 12, 52, 16, 12, then find(52) might return 3; insert(x,3) might make the list into 34, 12, 52, x, 16, 12 (if we insert after the position given); and delete(3) might turn that list into 34, 12, x, 16, 12.
Of course, the interpretation of what is appropriate for a function is entirely up to the programmer, as is the handling of special cases (for example, what does find(1) return above?). We could also add operations such as next and previous, which would take a position as argument and return the position of the successor and predecessor, respectively.
Obviously all of these instructions can be implemented just by using an array. Even if the array is dynamically allocated, an estimate of the maximum size of the list is required. Usually this requires a high over-estimate, which wastes considerable space. This could be a serious limitation, especially if there are many lists of unknown size.
An array implementation allows print_list and find to be carried out in linear time, which is as good as can be expected, and the find_kth operation takes constant time. However, insertion and deletion are expensive. For example, inserting at position 0 (which amounts to making a new first element) requires first pushing the entire array down one spot to make room, whereas deleting the first element requires shifting all the elements in the list up one, so the worst case of these operations is O(n). On average, half the list needs to be moved for either operation, so linear time is still required. Merely building a list by n successive inserts would require quadratic time.
Because the running time for insertions and deletions is so slow and the list size must be known in advance, simple arrays are generally not used to implement lists.
In order to avoid the linear cost of insertion and deletion, we need to ensure that the list is not stored contiguously, since otherwise entire parts of the list will need to be moved. Figure 3.1 shows the general idea of a linked list.
The linked list consists of a series of structures, which are not necessarily adjacent in memory. Each structure contains the element and a pointer to a structure containing its successor. We call this the next pointer. The last cell's next pointer points to ; this value is defined by C and cannot be confused with another pointer. ANSI C specifies that is zero.
Recall that a pointer variable is just a variable that contains the address where some other data is stored. Thus, if p is declared to be a pointer to a structure, then the value stored in p is interpreted as the location, in main memory, where a structure can be found. A field of that structure can be accessed by p
To execute print_list(L) or find(L,key), we merely pass a pointer to the first element in the list and then traverse the list by following the next pointers. This operation is clearly linear-time, although the constant is likely to be larger than if an array implementation were used. The find_kth operation is no longer quite as efficient as an array implementation; find_kth(L,i) takes O(i) time and works by traversing down the list in the obvious manner. In practice, this bound is pessimistic, because frequently the calls to find_kth are in sorted order (by i). As an example, find_kth(L,2), find_kth(L,3), find_kth(L,4), find_kth(L,6) can all be executed in one scan down the list.
The delete command can be executed in one pointer change. Figure 3.3 shows the result of deleting the third element in the original list.
The insert command requires obtaining a new cell from the system by using an malloc call (more on this later) and then executing two pointer maneuvers. The general idea is shown in Figure 3.4. The dashed line represents the old pointer.
The description above is actually enough to get everything working, but there are several places where you are likely to go wrong. First of all, there is no really obvious way to insert at the front of the list from the definitions given. Second, deleting from the front of the list is a special case, because it changes the start of the list; careless coding will lose the list. A third problem concerns deletion in general. Although the pointer moves above are simple, the deletion algorithm requires us to keep track of the cell before the one that we want to delete.
It turns out that one simple change solves all three problems. We will keep a sentinel node, which is sometimes referred to as a header or dummy node. This is a common practice, which we will see several times in the future. Our convention will be that the header is in position 0. Figure 3.5 shows a linked list with a header representing the list a1, a2, . . . , a5.
To avoid the problems associated with deletions, we need to write a routine find_previous, which will return the position of the predecessor of the cell we wish to delete. If we use a header, then if we wish to delete the first element in the list, find_previous will return the position of the header. The use of a header node is somewhat controversial. Some people argue that avoiding special cases is not sufficient justification for adding fictitious cells; they view the use of header nodes as little more than old-style hacking. Even so, we will use them here, precisely because they allow us to show the basic pointer manipulations without obscuring the code with special cases. Otherwise, whether or not a header should be used is a matter of personal preference.
As examples, we will write about half of the list ADT routines. First, we need our declarations, which are given in Figure 3.6.
The first function that we will write tests for an empty list. When we write code for any data structure that involves pointers, it is always best to draw a picture first. Figure 3.7 shows an empty list; from the figure it is easy to write the function in Figure 3.8.
The next function, which is shown in Figure 3.9, tests whether the current element, which by assumption exists, is the last of the list.
The next routine we will write is find. Find, shown in Figure 3.10, returns the position in the list of some element. Line 2 takes advantage of the fact that the and (&&) operation is short-circuited: if the first half of the and is false, the result is automatically false and the second half is not executed.
Some programmers find it tempting to code the find routine recursively, possibly because it avoids the sloppy termination condition. We shall see later that this is a very bad idea and should be avoided at all costs.
Our fourth routine will delete some element x in list L. We need to decide what to do if x occurs more than once or not at all. Our routine deletes the first occurrence of x and does nothing if x is not in the list. To do this, we find p, which is the cell prior to the one containing x, via a call to find_previous. The code to implement this is shown in Figure 3.11. The find_previous routine is similar to find and is shown in Figure 3.12.
The last routine we will write is an insertion routine. We will pass an element to be inserted along with the list L and a position p. Our particular insertion routine will insert an element after the position implied by p. This decision is arbitrary and meant to show that there are no set rules for what insertion does. It is quite possible to insert the new element into position p (which means before the element currently in position p), but doing this requires knowledge of the element before position p. This could be obtained by a call to find_previous. It is thus important to comment what you are doing. This has been done in Figure 3.13.
Notice that we have passed the list to the insert and is_last routines, even though it was never used. We did this because another implementation might need this information, and so not passing the list would defeat the idea of using ADTs.*
* This is legal, but some compilers will issue a warning.
With the exception of the find and find_previous routines, all of the operations we have coded take O(1) time. This is because in all cases only a fixed number of instructions are performed, no matter how large the list is. For the find and find_previous routines, the running time is O(n) in the worst case, because the entire list might need to be traversed if the element is either not found or is last in the list. On average, the running time is O(n), because on average, half the list must be traversed.
We could write additional routines to print a list and to perform the next function. These are fairly straightforward. We could also write a routine to implement previous. We leave these as exercises.
The most common error that you will get is that your program will crash with a nasty error message from the system, such as "memory access violation" or "segmentation violation." This message usually means that a pointer variable contained a bogus address. One common reason is failure to initialize the variable. For instance, if line 1 in Figure 3.14 is omitted, then p is undefined and is not likely to be pointing at a valid part of memory. Another typical error would be line 6 in Figure 3.13. If p is , then the indirection is illegal. This function knows that p is not , so the routine is OK. Of course, you should comment this so that the routine that calls insert will insure this. Whenever you do an indirection, you must make sure that the pointer is not NULL. Some C compliers will implicity do this check for you, but this is not part of the C standard. When you port a program from one compiler to another, you may find that it no longer works. This is one of the common reasons why.
The second common mistake concerns when and when not to use malloc to get a new cell. You must remember that declaring a pointer to a structure does not create the structure but only gives enough space to hold the address where some structure might be. The only way to create a record that is not already declared is to use the malloc command. The command malloc(size_p) has the system create, magically, a new structure and return a pointer to it. If, on the other hand, you want to use a pointer variable to run down a list, there is no need to declare a new structure; in that case the malloc command is inappropriate. A type cast is used to make both sides of the assignment operator compatible. The C library provides other variations of malloc such as calloc.
When things are no longer needed, you can issue a free command to inform the system that it may reclaim the space. A consequence of the free(p) command is that the address that p is pointing to is unchanged, but the data that resides at that address is now undefined.
If you never delete from a linked list, the number of calls to malloc should equal the size of the list, plus 1 if a header is used. Any less, and you cannot possibly have a working program. Any more, and you are wasting space and probably time. Occasionally, if your program uses a lot of space, the system may be unable to satisfy your request for a new cell. In this case a pointer is returned.
After a deletion in a linked list, it is usually a good idea to free the cell, especially if there are lots of insertions and deletions intermingled and memory might become a problem. You need to keep a temporary variable set to the cell to be disposed of, because after the pointer moves are finished, you will not have a reference to it. As an example, the code in Figure 3.14 is not the correct way to delete an entire list (although it may work on some systems).
Figure 3.15 shows the correct way to do this. Disposal is not necessarily a fast thing, so you might want to check to see if the disposal routine is causing any slow performance and comment it out if this is the case. This author has written a program (see the exercises) that was made 25 times faster by commenting out the disposal (of 10,000 nodes). It turned out that the cells were freed in a rather peculiar order and apparently caused an otherwise linear program to spend O(n log n) time to dispose of n cells.
One last warning: malloc(sizeof node_ptr) is legal, but it doesn't allocate enough space for a structure. It allocates space only for a pointer.
Sometimes it is convenient to traverse lists backwards. The standard implementation does not help here, but the solution is simple. Merely add an extra field to the data structure, containing a pointer to the previous cell. The cost of this is an extra link, which adds to the space requirement and also doubles the cost of insertions and deletions because there are more pointers to fix. On the other hand, it simplifies deletion, because you no longer have to refer to a key by using a pointer to the previous cell; this information is now at hand. Figure 3.16 shows a doubly linked list.
A popular convention is to have the last cell keep a pointer back to the first. This can be done with or without a header (if the header is present, the last cell points to it), and can also be done with doubly linked lists (the first cell's previous pointer points to the last cell). This clearly affects some of the tests, but the structure is popular in some applications. Figure 3.17 shows a double circularly linked list with no header.
We provide three examples that use linked lists. The first is a simple way to represent single-variable polynomials. The second is a method to sort in linear time, for some special cases. Finally, we show a complicated example of how linked lists might be used to keep track of course registration at a university.
We can define an abstract data type for single-variable polynomials (with nonnegative exponents) by using a list. Let
An alternative is to use a singly linked list. Each term in the polynomial is contained in one cell, and the cells are sorted in decreasing order of exponents. For instance, the linked lists in Figure 3.22 represent p1(x) and p2(x). We could then use the declarations in Figure 3.23.
The operations would then be straightforward to implement. The only potential difficulty is that when two polynomials are multiplied, the resultant polynomial will have to have like terms combined. There are several ways to do this, but we will leave this as an exercise.
A second example where linked lists are used is called radix sort. Radix sort is sometimes known as card sort, because it was used, until the advent of modern computers, to sort old-style punch cards.
If we have n integers in the range 1 to m (or 0 to m - 1) 9, we can use this information to obtain a fast sort known as bucket sort. We keep an array called count, of size m, which is initialized to zero. Thus, count has m cells (or buckets), which are initially empty. When ai is read, increment (by one) count[ai]. After all the input is read, scan the count array, printing out a representation of the sorted list. This algorithm takes O(m + n); the proof is left as an exercise. If m =
Radix sort is a generalization of this. The easiest way to see what happens is by example. Suppose we have 10 numbers, in the range 0 to 999, that we would like to sort. In general, this is n numbers in the range 0 to np - 1 for some constant p. Obviously, we cannot use bucket sort; there would be too many buckets. The trick is to use several passes of bucket sort. The natural algorithm would be to bucket-sort by the most significant "digit" (digit is taken to base n), then next most significant, and so on. That algorithm does not work, but if we perform bucket sorts by least significant "digit" first, then the algorithm works. Of course, more than one number could fall into the same bucket, and, unlike the original bucket sort, these numbers could be different, so we keep them in a list. Notice that all the numbers could have some digit in common, so if a simple array were used for the lists, then each array would have to be of size n, for a total space requirement of
The following example shows the action of radix sort on 10 numbers. The input is 64, 8, 216, 512, 27, 729, 0, 1, 343, 125 (the first ten cubes arranged randomly). The first step bucket sorts by the least significant digit. In this case the math is in base 10 (to make things simple), but do not assume this in general. The buckets are as shown in Figure 3.24, so the list, sorted by least significant digit, is 0, 1, 512, 343, 64, 125, 216, 27, 8, 729. These are now sorted by the next least significant digit (the tens digit here) (see Fig. 3.25). Pass 2 gives output 0, 1, 8, 512, 216, 125, 27, 729, 343, 64. This list is now sorted with respect to the two least significant digits. The final pass, shown in Figure 3.26, bucket-sorts by most significant digit. The final list is 0, 1, 8, 27, 64, 125, 216, 343, 512, 729.
To see that the algorithm works, notice that the only possible failure would occur if two numbers came out of the same bucket in the wrong order. But the previous passes ensure that when several numbers enter a bucket, they enter in sorted order. The running time is O(p(n + b)) where p is the number of passes, n is the number of elements to sort, and b is the number of buckets. In our case, b = n.
As an example, we could sort all integers that are representable on a computer (32 bits) by radix sort, if we did three passes over a bucket size of 211. This algorithm would always be O(n) on this computer, but probably still not as efficient as some of the algorithms we shall see in Chapter 7, because of the high constant involved (remember that a factor of log n is not all that high, and this algorithm would have the overhead of maintaining linked lists).
Our last example shows a more complicated use of linked lists. A university with 40,000 students and 2,500 courses needs to be able to generate two types of reports. The first report lists the class registration for each class, and the second report lists, by student, the classes that each student is registered for.
The obvious implementation might be to use a two-dimensional array. Such an array would have 100 million entries. The average student registers for about three courses, so only 120,000 of these entries, or roughly 0.1 percent, would actually have meaningful data.
What is needed is a list for each class, which contains the students in the class. We also need a list for each student, which contains the classes the student is registered for. Figure 3.27 shows our implementation.
As the figure shows, we have combined two lists into one. All lists use a header and are circular. To list all of the students in class C3, we start at C3 and traverse its list (by going right). The first cell belongs to student S1. Although there is no explicit information to this effect, this can be determined by following the student's linked list until the header is reached. Once this is done, we return to C3's list (we stored the position we were at in the course list before we traversed the student's list) and find another cell, which can be determined to belong to S3. We can continue and find that S4 and S5 are also in this class. In a similar manner, we can determine, for any student, all of the classes in which the student is registered.
Using a circular list saves space but does so at the expense of time. In the worst case, if the first student was registered for every course, then every entry would need to be examined in order to determine all the course names for that student. Because in this application there are relatively few courses per student and few students per course, this is not likely to happen. If it were suspected that this could cause a problem, then each of the (nonheader) cells could have pointers directly back to the student and class header. This would double the space requirement, but simplify and speed up the implementation.
Many languages, such as BASIC and FORTRAN, do not support pointers. If linked lists are required and pointers are not available, then an alternate implementation must be used. The alternate method we will describe is known as a cursor implementation.
The two important items present in a pointer implementation of linked lists are
1. The data is stored in a collection of structures. Each structure contains the data and a pointer to the next structure.
2. A new structure can be obtained from the system's global memory by a call to malloc and released by a call to free.
Our cursor implementation must be able to simulate this. The logical way to satisfy condition 1 is to have a global array of structures. For any cell in the array, its array index can be used in place of an address. Figure 3.28 gives the type declarations for a cursor implementation of linked lists.
We must now simulate condition 2 by allowing the equivalent of malloc and free for cells in the CURSOR_SPACE array. To do this, we will keep a list (the freelist) of cells that are not in any list. The list will use cell 0 as a header. The initial configuration is shown in Figure 3.29.
A value of 0 for next is the equivalent of a pointer. The initialization of CURSOR_SPACE is a straightforward loop, which we leave as an exercise. To perform an malloc, the first element (after the header) is removed from the freelist.
To perform a free, we place the cell at the front of the freelist. Figure 3.30 shows the cursor implementation of malloc and free. Notice that if there is no space available, our routine does the correct thing by setting p = 0. This indicates that there are no more cells left, and also makes the second line of cursor_new a nonoperation (no-op).
Given this, the cursor implementation of linked lists is straightforward. For consistency, we will implement our lists with a header node. As an example, in Figure 3.31, if the value of L is 5 and the value of M is 3, then L represents the list a, b, e, and M represents the list c, d, f.
To write the functions for a cursor implementation of linked lists, we must pass and return the identical parameters as the pointer implementation. The routines are straightforward. Figure 3.32 implements a function to test whether a list is empty. Figure 3.33 implements the test of whether the current position is the last in a linked list.
The function find in Figure 3.34 returns the position of x in list L.
The code to implement deletion is shown in Figure 3.35. Again, the interface for the cursor implementation is identical to the pointer implementation. Finally, Figure 3.36 shows a cursor implementation of insert.
The rest of the routines are similarly coded. The crucial point is that these routines follow the ADT specification. They take specific arguments and perform specific operations. The implementation is transparent to the user. The cursor implementation could be used instead of the linked list implementation, with virtually no change required in the rest of the code.
The freelist represents an interesting data structure in its own right. The cell that is removed from the freelist is the one that was most recently placed there by virtue of free. Thus, the last cell placed on the freelist is the first cell taken off. The data structure that also has this property is known as a stack, and is the topic of the next section.
A stack is a list with the restriction that inserts and deletes can be performed in only one position, namely the end of the list called the top. The fundamental operations on a stack are push, which is equivalent to an insert, and pop, which deletes the most recently inserted element. The most recently inserted element can be examined prior to performing a pop by use of the top routine. A pop or top on an empty stack is generally considered an error in the stack ADT. On the other hand, running out of space when performing a push is an implementation error but not an ADT error.
Stacks are sometimes known as LIFO (last in, first out) lists. The model depicted in Figure 3.37 signifies only that pushes are input operations and pops and tops are output. The usual operations to make empty stacks and test for emptiness are part of the repertoire, but essentially all that you can do to a stack is push and pop.
Figure 3.38 shows an abstract stack after several operations. The general model is that there is some element that is at the top of the stack, and it is the only element that is visible.
Of course, since a stack is a list, any list implementation will do. We will give two popular implementations. One uses pointers and the other uses an array, but, as we saw in the previous section, if we use good programming principles the calling routines do not need to know which method is being used.
The first implementation of a stack uses a singly linked list. We perform a push by inserting at the front of the list. We perform a pop by deleting the element at the front of the list. A top operation merely examines the element at the front of the list, returning its value. Sometimes the pop and top operations are combined into one. We could use calls to the linked list routines of the previous section, but we will rewrite the stack routines from scratch for the sake of clarity.
First, we give the definitions in Figure 3.39. We implement the stack using a header. Then Figure 3.40 shows that an empty stack is tested for in the same manner as an empty list.
Creating an empty stack is also simple. We merely create a header node; make_null sets the next pointer to NULL (see Fig. 3.41). The push is implemented as an insertion into the front of a linked list, where the front of the list serves as the top of the stack (see Fig. 3.42). The top is performed by examining the element in the first position of the list (see Fig. 3.43). Finally, we implement pop as a delete from the front of the list (see Fig. 3.44).
It should be clear that all the operations take constant time, because nowhere in any of the routines is there even a reference to the size of the stack (except for emptiness), much less a loop that depends on this size. The drawback of this implementation is that the calls to malloc and free are expensive, especially in comparison to the pointer manipulation routines. Some of this can be avoided by using a second stack, which is initially empty. When a cell is to be disposed from the first stack, it is merely placed on the second stack. Then, when new cells are needed for the first stack, the second stack is checked first.
An alternative implementation avoids pointers and is probably the more popular solution. The only potential hazard with this strategy is that we need to declare an array size ahead of time. Generally this is not a problem, because in typical applications, even if there are quite a few stack operations, the actual number of elements in the stack at any time never gets too large. It is usually easy to declare the array to be large enough without wasting too much space. If this is not possible, then a safe course would be to use a linked list implementation.
If we use an array implementation, the implementation is trivial. Associated with each stack is the top of stack, tos, which is -1 for an empty stack (this is how an empty stack is initialized). To push some element x onto the stack, we increment tos and then set STACK[tos] = x, where STACK is the array representing the actual stack. To pop, we set the return value to STACK[tos] and then decrement tos. Of course, since there are potentially several stacks, the STACK array and tos are part of one structure representing a stack. It is almost always a bad idea to use global variables and fixed names to represent this (or any) data structure, because in most real-life situations there will be more than one stack. When writing your actual code, you should attempt to follow the model as closely as possible, so that no part of your code, except for the stack routines, can attempt to access the array or top-of-stack variable implied by each stack. This is true for all ADT operations. Modern languages such as Ada and C++ can actually enforce this rule.
Notice that these operations are performed in not only constant time, but very fast constant time. On some machines, pushes and pops (of integers) can be written in one machine instruction, operating on a register with auto-increment and auto-decrement addressing. The fact that most modern machines have stack operations as part of the instruction set enforces the idea that the stack is probably the most fundamental data structure in computer science, after the array.
One problem that affects the efficiency of implementing stacks is error testing. Our linked list implementation carefully checked for errors. As described above, a pop on an empty stack or a push on a full stack will overflow the array bounds and cause a crash. This is obviously undesirable, but if checks for these conditions were put in the array implementation, they would likely take as much time as the actual stack manipulation. For this reason, it has become a common practice to skimp on error checking in the stack routines, except where error handling is crucial (as in operating systems). Although you can probably get away with this in most cases by declaring the stack to be large enough not to overflow and ensuring that routines that use pop never attempt to pop an empty stack, this can lead to code that barely works at best, especially when programs get large and are written by more than one person or at more than one time. Because stack operations take such fast constant time, it is rare that a significant part of the running time of a program is spent in these routines. This means that it is generally not justifiable to omit error checks. You should always write the error checks; if they are redundant, you can always comment them out if they really cost too much time. Having said all this, we can now write routines to implement a general stack using arrays.
A STACK is defined in Figure 3.45 as a pointer to a structure. The structure contains the top_of_stack and stack_size fields. Once the maximum size is known, the stack array can be dynamically allocated. Figure 3.46 creates a stack of a given maximum size. Lines 3-5 allocate the stack structure, and lines 6-8 allocate the stack array. Lines 9 and 10 initialize the top_of_stack and stack_size fields. The stack array does not need to be initialized. The stack is returned at line 11.
The routine dispose_stack should be written to free the stack structure. This routine first frees the stack array and then the stack structure (See Figure 3.47). Since create_stack requires an argument in the array implementation, but not in the linked list implementation, the routine that uses a stack will need to know which implementation is being used unless a dummy parameter is added for the later implementation. Unfortunately, efficiency and software idealism often create conflicts.
We have assumed that all stacks deal with the same type of element. In many languages, if there are different types of stacks, then we need to rewrite a new version of the stack routines for each different type, giving each version a different name. A cleaner alternative is provided in C++, which allows one to write a set of generic stack routines and essentially pass the type as an argument.* C++ also allows stacks of several different types to retain the same procedure and function names (such as push and pop): The compiler decides which routines are implied by checking the type of the calling routine.
*This is somewhat of an oversimplification.
Having said all this, we will now rewrite the four stack routines. In true ADT spirit, we will make the function and procedure heading look identical to the linked list implementation. The routines themselves are very simple and follow the written description exactly (see Figs. 3.48 to 3.52).
Pop is occasionally written as a function that returns the popped element (and alters the stack). Although current thinking suggests that functions should not change their input variables, Figure 3.53 illustrates that this is the most convenient method in C.
It should come as no surprise that if we restrict the operations allowed on a list, those operations can be performed very quickly. The big surprise, however, is that the small number of operations left are so powerful and important. We give three of the many applications of stacks. The third application gives a deep insight into how programs are organized.
Compilers check your programs for syntax errors, but frequently a lack of one symbol (such as a missing brace or comment starter) will cause the compiler to spill out a hundred lines of diagnostics without identifying the real error.
A useful tool in this situation is a program that checks whether everything is balanced. Thus, every right brace, bracket, and parenthesis must correspond to their left counterparts. The sequence [()] is legal, but [(]) is wrong. Obviously, it is not worthwhile writing a huge program for this, but it turns out that it is easy to check these things. For simplicity, we will just check for balancing of parentheses, brackets, and braces and ignore any other character that appears.
The simple algorithm uses a stack and is as follows:
Make an empty stack. Read characters until end of file. If the character is an open anything, push it onto the stack. If it is a close anything, then if the stack is empty report an error. Otherwise, pop the stack. If the symbol popped is not the corresponding opening symbol, then report an error. At end of file, if the stack is not empty report an error.
You should be able to convince yourself that this algorithm works. It is clearly linear and actually makes only one pass through the input. It is thus on-line and quite fast. Extra work can be done to attempt to decide what to do when an error is reported--such as identifying the likely cause.
Suppose we have a pocket calculator and would like to compute the cost of a shopping trip. To do so, we add a list of numbers and multiply the result by 1.06; this computes the purchase price of some items with local sales tax added. If the items are 4.99, 5.99, and 6.99, then a natural way to enter this would be the sequence
Depending on the calculator, this produces either the intended answer, 19.05, or the scientific answer, 18.39. Most simple four-function calculators will give the first answer, but better calculators know that multiplication has higher precedence than addition.
On the other hand, some items are taxable and some are not, so if only the first and last items were actually taxable, then the sequence
would give the correct answer (18.69) on a scientific calculator and the wrong answer (19.37) on a simple calculator. A scientific calculator generally comes with parentheses, so we can always get the right answer by parenthesizing, but with a simple calculator we need to remember intermediate results.
A typical evaluation sequence for this example might be to multiply 4.99 and 1.06, saving this answer as a1. We then add 5.99 and a1, saving the result in a1. We multiply 6.99 and 1.06, saving the answer in a2, and finish by adding al and a2, leaving the final answer in al. We can write this sequence of operations as follows:
This notation is known as postfix or reverse Polish notation and is evaluated exactly as we have described above. The easiest way to do this is to use a stack. When a number is seen, it is pushed onto the stack; when an operator is seen, the operator is applied to the two numbers (symbols) that are popped from the stack and the result is pushed onto the stack. For instance, the postfix expression
is evaluated as follows: The first four symbols are placed on the stack. The resulting stack is
Next a '+' is read, so 3 and 2 are popped from the stack and their sum, 5, is pushed.
Next 8 is pushed.
Now a '*' is seen, so 8 and 5 are popped as 8 * 5 = 40 is pushed.
Next a '+' is seen, so 40 and 5 are popped and 40 + 5 = 45 is pushed.
Now, 3 is pushed.
Next '+' pops 3 and 45 and pushes 45 + 3 = 48.
Finally, a '*' is seen and 48 and 6 are popped, the result 6 * 48 = 288 is pushed.
The time to evaluate a postfix expression is O(n), because processing each element in the input consists of stack operations and thus takes constant time. The algorithm to do so is very simple. Notice that when an expression is given in postfix notation, there is no need to know any precedence rules; this is an obvious advantage.
Not only can a stack be used to evaluate a postfix expression, but we can also use a stack to convert an expression in standard form (otherwise known as infix) into postfix. We will concentrate on a small version of the general problem by allowing only the operators +, *, and (, ), and insisting on the usual precedence rules. We will further assume that the expression is legal. Suppose we want to convert the infix expression
into postfix. A correct answer is a b c * + d e * f + g * +.
When an operand is read, it is immediately placed onto the output. Operators are not immediately output, so they must be saved somewhere. The correct thing to do is to place operators that have been seen, but not placed on the output, onto the stack. We will also stack left parentheses when they are encountered. We start with an initially empty stack.
If we see a right parenthesis, then we pop the stack, writing symbols until we encounter a (corresponding) left parenthesis, which is popped but not output.
If we see any other symbol ('+','*', '(' ), then we pop entries from the stack until we find an entry of lower priority. One exception is that we never remove a '(' from the stack except when processing a ')'. For the purposes of this operation, '+' has lowest priority and '(' highest. When the popping is done, we push the operand onto the stack.
Finally, if we read the end of input, we pop the stack until it is empty, writing symbols onto the output.
To see how this algorithm performs, we will convert the infix expression above into its postfix form. First, the symbol a is read, so it is passed through to the output. Then '+' is read and pushed onto the stack. Next b is read and passed through to the output. The state of affairs at this juncture is as follows:
Next a '*' is read. The top entry on the operator stack has lower precedence than '*', so nothing is output and '*' is put on the stack. Next, c is read and output. Thus far, we have
The next symbol is a '+'. Checking the stack, we find that we will pop a '*' and place it on the output, pop the other '+', which is not of lower but equal priority, on the stack, and then push the '+'.
The next symbol read is an '(', which, being of highest precedence, is placed on the stack. Then d is read and output.
We continue by reading a '*'. Since open parentheses do not get removed except when a closed parenthesis is being processed, there is no output. Next, e is read and output.
The next symbol read is a '+'. We pop and output '*' and then push '+'. Then we read and output
Now we read a ')', so the stack is emptied back to the '('. We output a '+'.
We read a '*' next; it is pushed onto the stack. Then g is read and output.
The input is now empty, so we pop and output symbols from the stack until it is empty.
As before, this conversion requires only O(n) time and works in one pass through the input. We can add subtraction and division to this repertoire by assigning subtraction and addition equal priority and multiplication and division equal priority. A subtle point is that the expression a - b - c will be converted to ab - c- and not abc - -. Our algorithm does the right thing, because these operators associate from left to right. This is not necessarily the case in general, since exponentiation associates right to left: 223 = 28 = 256 not 43 = 64. We leave as an exercise the problem of adding exponentiation to the repertoire of assignments.
The algorithm to check balanced symbols suggests a way to implement function calls. The problem here is that when a call is made to a new function, all the variables local to the calling routine need to be saved by the system, since otherwise the new function will overwrite the calling routine's variables. Furthermore, the current location in the routine must be saved so that the new function knows where to go after it is done. The variables have generally been assigned by the compiler to machine registers, and there are certain to be conflicts (usually all procedures get some variables assigned to register #1), especially if recursion is involved. The reason that this problem is similar to balancing symbols is that a function call and function return are essentially the same as an open parenthesis and closed parenthesis, so the same ideas should work.
When there is a function call, all the important information that needs to be saved, such as register values (corresponding to variable names) and the return address (which can be obtained from the program counter, which is typically in a register), is saved "on a piece of paper" in an abstract way and put at the top of a pile. Then the control is transferred to the new function, which is free to replace the registers with its values. If it makes other function calls, it follows the same procedure. When the function wants to return, it looks at the "paper" at the top of the pile and restores all the registers. It then makes the return jump.
Clearly, all of this work can be done using a stack, and that is exactly what happens in virtually every programming language that implements recursion. The information saved is called either an activation record or stack frame. The stack in a real computer frequently grows from the high end of your memory partition downwards, and on many systems there is no checking for overflow. There is always the possibility that you will run out of stack space by having too many simultaneously active functions. Needless to say, running out of stack space is always a fatal error.
In languages and systems that do not check for stack overflow, your program will crash without an explicit explanation. On these systems, strange things may happen when your stack gets too big, because your stack will run into part of your program. It could be the main program, or it could be part of your data, especially if you have a big array. If it runs into your program, your program will be corrupted; you will have nonsense instructions and will crash as soon as they are executed. If the stack runs into your data, what is likely to happen is that when you write something into your data, it will destroy stack information -- probably the return address -- and your program will attempt to return to some weird address and crash.
In normal events, you should not run out of stack space; doing so is usually an indication of runaway recursion (forgetting a base case). On the other hand, some perfectly legal and seemingly innocuous program can cause you to run out of stack space. The routine in Figure 3.54, which prints out a linked list, is perfectly legal and actually correct. It properly handles the base case of an empty list, and the recursion is fine. This program can be proven correct. Unfortunately, if the list contains 20,000 elements, there will be a stack of 20,000 activation records representing the nested calls of line 3. Activation records are typically large because of all the information they contain, so this program is likely to run out of stack space. (If 20,000 elements are not enough to make the program crash, replace the number with a larger one.)
This program is an example of an extremely bad use of recursion known as tail recursion. Tail recursion refers to a recursive call at the last line. Tail recursion can be mechanically eliminated by changing the recursive call to a goto preceded by one assignment per function argument. This simulates the recursive call because nothing needs to be saved -- after the recursive call finishes, there is really no need to know the saved values. Because of this, we can just go to the top of the function with the values that would have been used in a recursive call. The program in Figure 3.55 shows the improved version. Keep in mind that you should use the more natural while loop construction. The goto is used here to show how a compiler might automatically remove the recursion.
Removal of tail recursion is so simple that some compilers do it automatically. Even so, it is best not to find out that yours does not.
Recursion can always be completely removed (obviously, the compiler does so in converting to assembly language), but doing so can be quite tedious. The general strategy requires using a stack and is obviously worthwhile only if you can manage to put only the bare minimum on the stack. We will not dwell on this further, except to point out that although nonrecursive programs are certainly generally faster than recursive programs, the speed advantage rarely justifies the lack of clarity that results from removing the recursion.
Like stacks, queues are lists. With a queue, however, insertion is done at one end, whereas deletion is performed at the other end.
The basic operations on a queue are enqueue, which inserts an element at the end of the list (called the rear), and dequeue, which deletes (and returns) the element at the start of the list (known as the front). Figure 3.56 shows the abstract model of a queue.
As with stacks, any list implementation is legal for queues. Like stacks, both the linked list and array implementations give fast O(1) running times for every operation. The linked list implementation is straightforward and left as an exercise. We will now discuss an array implementation of queues.
For each queue data structure, we keep an array, QUEUE[], and the positions q_front and q_rear, which represent the ends of the queue. We also keep track of the number of elements that are actually in the queue, q_size. All this information is part of one structure, and as usual, except for the queue routines themselves, no routine should ever access these directly. The following figure shows a queue in some intermediate state. By the way, the cells that are blanks have undefined values in them. In particular, the first two cells have elements that used to be in the queue.
The operations should be clear. To enqueue an element x, we increment q_size and q_rear, then set QUEUE[q_rear] = x. To dequeue an element, we set the return value to QUEUE[q_front], decrement q_size, and then increment q_front. Other strategies are possible (this is discussed later). We will comment on checking for errors presently.
There is one potential problem with this implementation. After 10 enqueues, the queue appears to be full, since q_front is now 10, and the next enqueue would be in a nonexistent position. However, there might only be a few elements in the queue, because several elements may have already been dequeued. Queues, like stacks, frequently stay small even in the presence of a lot of operations.
The simple solution is that whenever q_front or q_rear gets to the end of the array, it is wrapped around to the beginning. The following figure shows the queue during some operations. This is known as a circular array implementation.
The extra code required to implement the wraparound is minimal (although it probably doubles the running time). If incrementing either q_rear or q_front causes it to go past the array, the value is reset to the first position in the array.
There are two warnings about the circular array implementation of queues. First, it is important to check the queue for emptiness, because a dequeue when the queue is empty will return an undefined value, silently.
Secondly, some programmers use different ways of representing the front and rear of a queue. For instance, some do not use an entry to keep track of the size, because they rely on the base case that when the queue is empty, q_rear = q_front - 1. The size is computed implicitly by comparing q_rear and q_front. This is a very tricky way to go, because there are some special cases, so be very careful if you need to modify code written this way. If the size is not part of the structure, then if the array size is A_SIZE, the queue is full when there are A_SIZE -1 elements, since only A_SIZE different sizes can be differentiated, and one of these is 0. Pick any style you like and make sure that all your routines are consistent. Since there are a few options for implementation, it is probably worth a comment or two in the code, if you don't use the size field.
In applications where you are sure that the number of enqueues is not larger than the size of the queue, obviously the wraparound is not necessary. As with stacks, dequeues are rarely performed unless the calling routines are certain that the queue is not empty. Thus error calls are frequently skipped for this operation, except in critical code. This is generally not justifiable, because the time savings that you are likely to achieve are too minimal.
We finish this section by writing some of the queue routines. We leave the others as an exercise to the reader. First, we give the type definitions in Figure 3.57. We add a maximum size field, as was done for the array implementation of the stack; queue_create and queue_dispose routines also need to be provided. We also provide routines to test whether a queue is empty and to make an empty queue (Figs. 3.58 and 3.59). The reader can write the function is_full, which performs the test implied by its name. Notice that q_rear is preinitialized to 1 before q_front. The final operation we will write is the enqueue routine. Following the exact description above, we arrive at the implementation in Figure 3.60.
There are several algorithms that use queues to give efficient running times. Several of these are found in graph theory, and we will discuss them later in Chapter 9. For now, we will give some simple examples of queue usage.
When jobs are submitted to a printer, they are arranged in order of arrival. Thus, essentially, jobs sent to a line printer are placed on a queue.*
*We say essentially a queue, because jobs can be killed. This amounts to a deletion from the middle of the queue, which is a violation of the strict definition.
Virtually every real-life line is (supposed to be) a queue. For instance, lines at ticket counters are queues, because service is first-come first-served.
Another example concerns computer networks. There are many network setups of personal computers in which the disk is attached to one machine, known as the file server. Users on other machines are given access to files on a first-come first-served basis, so the data structure is a queue.
Further examples include the following:
A whole branch of mathematics, known as queueing theory, deals with computing, probabilistically, how long users expect to wait on a line, how long the line gets, and other such questions. The answer depends on how frequently users arrive to the line and how long it takes to process a user once the user is served. Both of these parameters are given as probability distribution functions. In simple cases, an answer can be computed analytically. An example of an easy case would be a phone line with one operator. If the operator is busy, callers are placed on a waiting line (up to some maximum limit). This problem is important for businesses, because studies have shown that people are quick to hang up the phone.
If there are k operators, then this problem is much more difficult to solve. Problems that are difficult to solve analytically are often solved by a simulation. In our case, we would need to use a queue to perform the simulation. If k is large, we also need other data structures to do this efficiently. We shall see how to do this simulation in Chapter 6. We could then run the simulation for several values of k and choose the minimum k that gives a reasonable waiting time.
Additional uses for queues abound, and as with stacks, it is staggering that such a simple data structure can be so important.
This chapter describes the concept of ADTs and illustrates the concept with three of the most common abstract data types. The primary objective is to separate the implementation of the abstract data types from their function. The program must know what the operations do, but it is actually better off not knowing how it is done.
Lists, stacks, and queues are perhaps the three fundamental data structures in all of computer science, and their use is documented through a host of examples. In particular, we saw how stacks are used to keep track of procedure and function calls and how recursion is actually implemented. This is important to understand, not just because it makes procedural languages possible, but because knowing how recursion is implemented removes a good deal of the mystery that surrounds its use. Although recursion is very powerful, it is not an entirely free operation; misuse and abuse of recursion can result in programs crashing.
3.1 Write a program to print out the elements of a singly linked list.
3.2 You are given a linked list, L, and another linked list, P, containing integers, sorted in ascending order. The operation print_lots(L,P) will print the elements in L that are in positions specified by P. For instance, if P = 1, 3, 4, 6, the first, third, fourth, and sixth elements in L are printed. Write the routine print_lots(L,P). You should use only the basic list operations. What is the running time of your routine?
3.3 Swap two adjacent elements by adjusting only the pointers (and not the data) using
a. singly linked lists,
b. doubly linked lists.
3.4 Given two sorted lists, L1 and L2, write a procedure to compute L1
3.5 Given two sorted lists, L1 and L2, write a procedure to compute L1
3.6 Write a function to add two polynomials. Do not destroy the input. Use a linked list implementation. If the polynomials have m and n terms respectively, what is the time complexity of your program?
3.7 Write a function to multiply two polynomials, using a linked list implementation. You must make sure that the output polynomial is sorted by exponent and has at most one term of any power.
a. Give an algorithm to solve this problem in O(m2n2) time.
*b. Write a program to perform the multiplication in O(m2n) time, where m is the number of terms in the polynomial of fewer terms.
*c. Write a program to perform the multiplication in O(mn log(mn)) time.
d. Which time bound above is the best?
3.8 Write a program that takes a polynomial,
3.9 Write an arbitrary-precision integer arithmetic package. You should use a strategy similar to polynomial arithmetic. Compute the distribution of the digits 0 to 9 in 24000.
3.10 The Josephus problem is the following mass suicide "game": n people, numbered 1 to n, are sitting in a circle. Starting at person 1, a handgun is passed. After m passes, the person holding the gun commits suicide, the body is removed, the circle closes ranks, and the game continues with the person who was sitting after the corpse picking up the gun. The last survivor is tried for n - 1 counts of manslaughter. Thus, if m = 0 and n = 5, players are killed in order and player 5 stands trial. If m = 1 and n = 5, the order of death is 2, 4, 1, 5.
a. Write a program to solve the Josephus problem for general values of m and n. Try to make your program as efficient as possible. Make sure you dispose of cells.
b. What is the running time of your program?
c. If m = 1, what is the running time of your program? How is the actual speed affected by the free routine for large values of n (n > 10000)?
3.11 Write a program to find a particular element in a singly linked list. Do this both recursively and nonrecursively, and compare the running times. How big does the list have to be before the recursive version crashes?
3.12 a. Write a nonrecursive procedure to reverse a singly linked list in O(n) time.
*b. Write a procedure to reverse a singly linked list in O(n) time using constant extra space.
3.13 You have to sort an array of student records by social security number. Write a program to do this, using radix sort with 1000 buckets and three passes.
3.14 Write a program to read a graph into adjacency lists using
a. linked lists
b. cursors
3.15 a. Write an array implementation of self-adjusting lists. A self-adjusting list is like a regular list, except that all insertions are performed at the front, and when an element is accessed by a find, it is moved to the front of the list without changing the relative order of the other items.
b. Write a linked list implementation of self-adjusting lists.
*c. Suppose each element has a fixed probability, pi, of being accessed. Show that the elements with highest access probability are expected to be close to the front.
3.16 Suppose we have an array-based list a[0..n -1] and we want to delete all duplicates. last_position is initially n - 1, but gets smaller as elements are deleted. Consider the pseudocode program fragment in Figure 3.61. The procedure DELETE deletes the element in position j and collapses the list.
a. Explain how this procedure works.
b. Rewrite this procedure using general list operations.
*c. Using a standard array implementation, what is the running time of this procedure?
d. What is the running time using a linked list implementation?
*e. Give an algorithm to solve this problem in O(n log n) time.
**f. Prove that any algorithm to solve this problem requires
*g. Prove that if we allow operations besides comparisons, and the keys are real numbers, then we can solve the problem without using comparisons between elements.
3.17 An alternative to the deletion strategy we have given is to use lazy deletion. To delete an element, we merely mark it deleted (using an extra bit field). The number of deleted and nondeleted elements in the list is kept as part of the data structure. If there are as many deleted elements as nondeleted elements, we traverse the entire list, performing the standard deletion algorithm on all marked nodes.
a. List the advantages and disadvantages of lazy deletion.
b. Write routines to implement the standard linked list operations using lazy deletion.
3.18 Write a program to check for balancing symbols in the following languages:
a. Pascal (begin/end, ( ), [ ], { }).
b. C (/* */, ( ), [ ], { }).
*c. Explain how to print out an error message that is likely to reflect the probable cause.
3.19 Write a program to evaluate a postfix expression.
3.20 a. Write a program to convert an infix expression which includes '(', ')', '+', '-', '*' and '/' to postfix.
b. Add the exponentiation operator to your repertoire.
c. Write a program to convert a postfix expression to infix.
3.21 Write routines to implement two stacks using only one array. Your stack routines should not declare an overflow unless every slot in the array is used.
3.22 *a. Propose a data structure that supports the stack push and pop operations and a third operation find_min, which returns the smallest element in the data structure, all in O(1) worst case time.
*b. Prove that if we add the fourth operation delete_min which finds and removes the smallest element, then at least one of the operations must take
3.23 *Show how to implement three stacks in one array.
3.24 If the recursive routine in Section 2.4 used to compute Fibonacci numbers is run for n = 50, is stack space likely to run out? Why or why not?
3.25 Write the routines to implement queues using
a. linked lists
b. arrays
3.26 A deque is a data structure consisting of a list of items, on which the following operations are possible:
push(x,d): Insert item x on the front end of deque d.
pop(d): Remove the front item from deque d and return it.
inject(x,d): Insert item x on the rear end of deque d.
eject(d): Remove the rear item from deque d and return it.
Write routines to support the deque that take O(1) time per operation.
3.2. The List ADT
3.2.1. Simple Array Implementation of Lists
3.2.2. Linked Lists
field_name, where field_name is the name of the field we wish to examine. Figure 3.2 shows the actual representation of the list in Figure 3.1. The list contains five structures, which happen to reside in memory locations 1000, 800, 712, 992, and 692 respectively. The next pointer in the first structure has the value 800, which provides the indication of where the second structure is. The other structures each have a pointer that serves a similar purpose. Of course, in order to access this list, we need to know where the first cell can be found. A pointer variable can be used for this purpose. It is important to remember that a pointer is just a number. For the rest of this chapter, we will draw pointers with arrows, because they are more illustrative.
Figure 3.1 A linked list
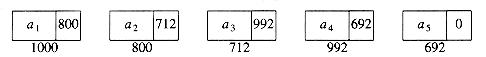
Figure 3.2 Linked list with actual pointer values
Figure 3.3 Deletion from a linked list
Figure 3.4 Insertion into a linked list
3.2.3. Programming Details
Figure 3.5 Linked list with a header
typedef struct node *node_ptr;
struct node
{element_type element;
node_ptr next;
};
typedef node_ptr LIST;
typedef node_ptr position;
Figure 3.6 Type declarations for linked lists
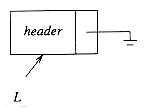
Figure 3.7 Empty list with header
int
is_empty( LIST L )
{return( L->next == NULL );
}
Figure 3.8 Function to test whether a linked list is empty
int
is_last( position p, LIST L )
{return( p->next == NULL );
}
Figure 3.9 Function to test whether current position is the last in a linked list
/* Return position of x in L; NULL if not found */
position
find ( element_type x, LIST L )
{position p;
/*1*/ p = L->next;
/*2*/ while( (p != NULL) && (p->element != x) )
/*3*/ p = p->next;
/*4*/ return p;
}
Figure 3.10 Find routine
/* Delete from a list. Cell pointed */
/* to by p->next is wiped out. */
/* Assume that the position is legal. */
/* Assume use of a header node. */
void
delete( element_type x, LIST L )
{position p, tmp_cell;
p = find_previous( x, L );
if( p->next != NULL ) /* Implicit assumption of header use */
{ /* x is found: delete it */tmp_cell = p->next;
p->next = tmp_cell->next; /* bypass the cell to be deleted */
free( tmp_cell );
}
}
Figure 3.11 Deletion routine for linked lists
/* Uses a header. If element is not found, then next field */
/* of returned value is NULL */
position
find_previous( element_type x, LIST L )
{position p;
/*1*/ p = L;
/*2*/ while( (p->next != NULL) && (p->next->element != x) )
/*3*/ p = p->next;
/*4*/ return p;
}
Figure 3.12 Find_previous--the find routine for use with delete
/* Insert (after legal position p).*/
/* Header implementation assumed. */
void
insert( element_type x, LIST L, position p )
{position tmp_cell;
/*1*/ tmp_cell = (position) malloc( sizeof (struct node) );
/*2*/ if( tmp_cell == NULL )
/*3*/ fatal_error("Out of space!!!");else
{/*4*/ tmp_cell->element = x;
/*5*/ tmp_cell->next = p->next;
/*6*/ p->next = tmp_cell;
}
}
Figure 3.13 Insertion routine for linked lists
3.2.4. Common Errors
void
delete_list( LIST L )
{position p;
/*1*/ p = L->next; /* header assumed */
/*2*/ L->next = NULL;
/*3*/ while( p != NULL )
{/*4*/ free( p );
/*5*/ p = p->next;
}
}
Figure 3.14 Incorrect way to delete a list
void
delete_list( LIST L )
{position p, tmp;
/*1*/ p = L->next; /* header assumed */
/*2*/ L->next = NULL;
/*3*/ while( p != NULL )
{/*4*/ tmp = p->next;
/*5*/ free( p );
/*6*/ p = tmp;
}
}
Figure 3.15 Correct way to delete a list
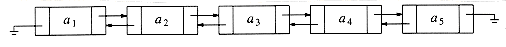
Figure 3.16 A doubly linked list
3.2.5. Doubly Linked Lists
3.2.6. Circularly Linked Lists
3.2.7. Examples
The Polynomial ADT
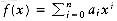. If most of the coefficients ai are nonzero, we can use a simple array to store the coefficients. We could then write routines to perform addition, subtraction, multiplication, differentiation, and other operations on these polynomials. In this case, we might use the type declarations given in Figure 3.18. We could then write routines to perform various operations. Two possibilities are addition and multiplication. These are shown in Figures 3.19 to 3.21. Ignoring the time to initialize the output polynomials to zero, the running time of the multiplication routine is proportional to the product of the degree of the two input polynomials. This is adequate for dense polynomials, where most of the terms are present, but if p1(x) = 10x1000 + 5x14 + 1 and p2(x) = 3x1990 - 2x1492 + 11x + 5, then the running time is likely to be unacceptable. One can see that most of the time is spent multiplying zeros and stepping through what amounts to nonexistent parts of the input polynomials. This is always undesirable.
Figure 3.17 A double circularly linked list
typedef struct
{int coeff_array[ MAX_DEGREE+1 ];
unsigned int high_power;
} *POLYNOMIAL;
Figure 3.18 Type declarations for array implementation of the polynomial ADT
void
zero_polynomial( POLYNOMIAL poly )
{unsigned int i;
for( i=0; i<=MAX_DEGREE; i++ )
poly->coeff_array[i] = 0;
poly->high_power = 0;
}
Figure 3.19 Procedure to initialize a polynomial to zero
void
add_polynomial( POLYNOMIAL poly1, POLYNOMIAL poly2,
POLYNOMIAL poly_sum )
{int i;
zero_polynomial( poly_sum );
poly_sum->high_power = max( poly1->high_power,
poly2->high_power);
for( i=poly_sum->high_power; i>=0; i-- )
poly_sum->coeff_array[i] = poly1->coeff_array[i]
+ poly2->coeff_array[i];
}
Figure 3.20 Procedure to add two polynomials
void
mult_polynomial( POLYNOMIAL poly1, POLYNOMIAL poly2,
POLYNOMIAL poly_prod )
{unsigned int i, j;
zero_polynomial( poly_prod );
poly_prod->high_power = poly1->high_power
+ poly2->high_power;
if( poly_prod->high_power > MAX_DEGREE )
error("Exceeded array size");else
for( i=0; i<=poly->high_power; i++ )
for( j=0; j<=poly2->high_power; j++ )
poly_prod->coeff_array[i+j] +=
poly1->coeff_array[i] * poly2->coeff_array[j];
}
Figure 3.21 Procedure to multiply two polynomials
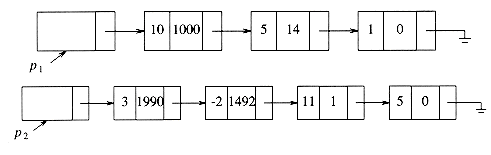
Figure 3.22 Linked list representations of two polynomials
typedef struct node *node_ptr;
struct node
{int coefficient;
int exponent;
node_ptr next;
} ;
typedef node_ptr POLYNOMIAL; /* keep nodes sorted by exponent */
Figure 3.23 Type declaration for linked list implementation of the Polynomial ADT
Radix Sort
(n), then bucket sort is O(n).(n2). 0 1 512 343 64 125 216 27 8 729
-------------------------------------------
0 1 2 3 4 5 6 7 8 9
Figure 3.24 Buckets after first step of radix sort
8 729
1 216 27
0 512 125 343 64
--------------------------------------
0 1 2 3 4 5 6 7 8 9
Figure 3.25 Buckets after the second pass of radix sort
64
27
8
1
0 125 216 343 512 729
------------------------------------------
0 1 2 3 4 5 6 7 8 9
Figure 3.26 Buckets after the last pass of radix sort
Multilists
Figure 3.27 Multilist implementation for registration problem
3.2.8. Cursor Implementation of Linked Lists
typedef unsigned int node_ptr;
struct node
{element_type element;
node_ptr next;
};
typedef node_ptr LIST;
typedef node_ptr position;
struct node CURSOR_SPACE[ SPACE_SIZE ];
Figure 3.28 Declarations for cursor implementation of linked lists
Slot Element Next
----------------------
0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 0
Figure 3.29 An initialized CURSOR_SPACE
position
cursor_alloc( void )
{position p;
p = CURSOR_SPACE[O].next;
CURSOR_SPACE[0].next = CURSOR_SPACE[p].next;
return p;
}
void
cursor_free( position p)
{CURSOR_SPACE[p].next = CURSOR_SPACE[O].next;
CURSOR_SPACE[O].next = p;
}
Figure 3.30 Routines: cursor-alloc and cursor-free
Slot Element Next
----------------------
0 - 6
1 b 9
2 f 0
3 header 7
4 - 0
5 header 10
6 - 4
7 c 8
8 d 2
9 e 0
10 a 1
Figure 3.31 Example of a cursor implementation of linked lists
int
is_empty( LIST L ) /* using a header node */
{return( CURSOR_SPACE[L].next == 0
}
Figure 3.32 Function to test whether a linked list is empty--cursor implementation
int
is_last( position p, LIST L) /* using a header node */
{return( CURSOR_SPACE[p].next == 0
}
Figure 3.33 Function to test whether p is last in a linked list--cursor implementation
position
find( element_type x, LIST L) /* using a header node */
{position p;
/*1*/ p = CURSOR_SPACE[L].next;
/*2*/ while( p && CURSOR_SPACE[p].element != x )
/*3*/ p = CURSOR_SPACE[p].next;
/*4*/ return p;
}
Figure 3.34 Find routine--cursor implementation
void
delete( element_type x, LIST L )
{position p, tmp_cell;
p = find_previous( x, L );
if( !is_last( p, L) )
{tmp_cell = CURSOR_SPACE[p].next;
CURSOR_SPACE[p].next = CURSOR_SPACE[tmp_cell].next;
cursor_free( tmp_cell );
}
}
Figure 3.35 Deletion routine for linked lists--cursor implementation
/* Insert (after legal position p); */
/* header implementation assumed */
void
insert( element_type x, LIST L, position p )
{position tmp_cell;
/*1*/ tmp_cell = cursor_alloc( )
/*2*/ if( tmp_cell ==0 )
/*3*/ fatal_error("Out of space!!!");else
{/*4*/ CURSOR_SPACE[tmp_cell].element = x;
/*5*/ CURSOR_SPACE[tmp_cell].next = CURSOR_SPACE[p].next;
/*6*/ CURSOR_SPACE[p].next = tmp_cell;
}
}
Figure 3.36 Insertion routine for linked lists--cursor implementation
3.3. The Stack ADT
3.3.1. Stack Model
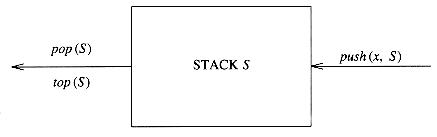
Figure 3.37 Stack model: input to a stack is by push, output is by pop
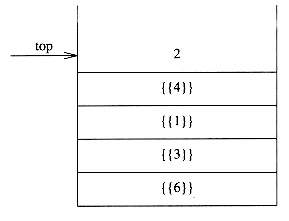
Figure 3.38 Stack model: only the top element is accessible
3.3.2. Implementation of Stacks
Linked List Implementation of Stacks
Array Implementation of Stacks
typedef struct node *node_ptr;
struct node
{element_type element;
node_ptr next;
};
typedef node_ptr STACK;
/* Stack implementation will use a header. */
Figure 3.39 Type declaration for linked list implementation of the stack ADT
int
is_empty( STACK S )
{return( S->next == NULL );
}
Figure 3.40 Routine to test whether a stack is empty-linked list implementation
STACK
create_stack( void )
{STACK S;
S = (STACK) malloc( sizeof( struct node ) );
if( S == NULL )
fatal_error("Out of space!!!");return S;
}
void
make_null( STACK S )
{if( S != NULL )
S->next = NULL;
else
error("Must use create_stack first");}
Figure 3.41 Routine to create an empty stack-linked list implementation
void
push( element_type x, STACK S )
{node_ptr tmp_cell;
tmp_cell = (node_ptr) malloc( sizeof ( struct node ) );
if( tmp_cell == NULL )
fatal_error("Out of space!!!");else
{tmp_cell->element = x;
tmp_cell->next = S->next;
S->next = tmp_cell;
}
}
Figure 3.42 Routine to push onto a stack-linked list implementation
element_type
top( STACK S )
{if( is_empty( S ) )
error("Empty stack");else
return S->next->element;
}
Figure 3.43 Routine to return top element in a stack--linked list implementation
void
pop( STACK S )
{node_ptr first_cell;
if( is_empty( S ) )
error("Empty stack");else
{first_cell = S->next;
S->next = S->next->next;
free( first_cell );
}
}
Figure 3.44 Routine to pop from a stack--linked list implementation
struct stack_record
{unsigned int stack_size;
int top_of_stack;
element_type *stack_array;
};
typedef struct stack_record *STACK;
#define EMPTY_TOS (-1) /* Signifies an empty stack */
Figure 3.45 STACK definition--array implementaion
STACK
create_stack( unsigned int max_elements )
{STACK S;
/*1*/ if( max_elements < MIN_STACK_SIZE )
/*2*/ error("Stack size is too small");/*3*/ S = (STACK) malloc( sizeof( struct stack_record ) );
/*4*/ if( S == NULL )
/*5*/ fatal_error("Out of space!!!");/*6*/ S->stack_array = (element_type *)
malloc( sizeof( element_type ) * max_elements );
/*7*/ if( S->stack_array == NULL )
/*8*/ fatal_error("Out of space!!!");/*9*/ S->top_of_stack = EMPTY_TOS;
/*10*/ S->stack_size = max_elements;
/*11*/ return( S );
}
Figure 3.46 Stack creation--array implementaion
void
dispose_stack( STACK S )
{if( S != NULL )
{free( S->stack_array );
free( S );
}
}
Figure 3.47 Routine for freeing stack--array implementation
int
is_empty( STACK S )
{return( S->top_of_stack == EMPTY_TOS );
}
Figure 3.48 Routine to test whether a stack is empty--array implementation
void
make_null( STACK S )
{S->top_of_stack = EMPTY_TOS;
}
Figure 3.49 Routine to create an empty stack--array implementation
void
push( element_type x, STACK S )
{if( is_full( S ) )
error("Full stack");else
S->stack_array[ ++S->top_of_stack ] = x;
}
Figure 3.50 Routine to push onto a stack--array implementation
element_type
top( STACK S )
{if( is_empty( S ) )
error("Empty stack");else
return S->stack_array[ S->top_of_stack ];
}
Figure 3.51 Routine to return top of stack--array implementation
void
pop( STACK S )
{if( is_empty( S ) )
error("Empty stack");else
S->top_of_stack--;
}
Figure 3.52 Routine to pop from a stack--array implementation
element_type
pop( STACK S )
{if( is_empty( S ) )
error("Empty stack");else
return S->stack_array[ S->top_of_stack-- ];
}
Figure 3.53 Routine to give top element and pop a stack--array implementation
3.3.3. Applications
Balancing Symbols
Postfix Expressions
4.99 + 5.99 + 6.99 * 1.06 =
4.99 * 1.06 + 5.99 + 6.99 * 1.06 =
4.99 1.06 * 5.99 + 6.99 1.06 * +
6 5 2 3 + 8 * + 3 + *
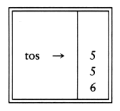
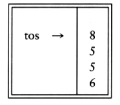
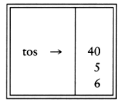
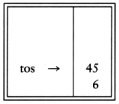
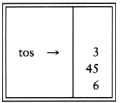
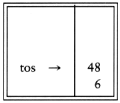
Infix to Postfix Conversion
a + b * c + ( d * e + f ) * g
.
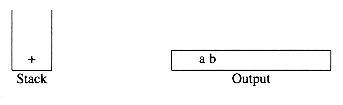
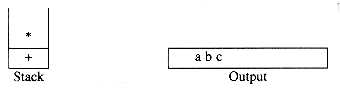
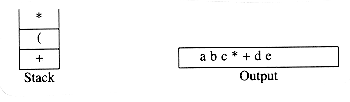
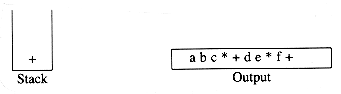
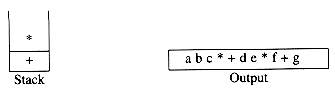
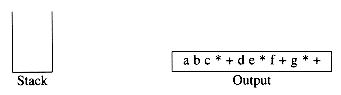
Function Calls
void /* Not using a header */
print_list( LIST L )
{/*1*/ if( L != NULL )
{/*2*/ print_element( L->element );
/*3*/ print_list( L->next );
}
}
Figure 3.54 A bad use of recursion: printing a linked list
void
print_list( LIST L ) /* No header */
{top:
if( L != NULL )
{print_element( L->element );
L = L->next;
goto top;
}
}
Figure 3.55 Printing a list without recursion; a compiler might do this (you should not)
3.4. The Queue ADT
3.4.1. Queue Model
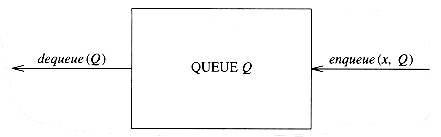
Figure 3.56 Model of a queue
3.4.2. Array Implementation of Queues
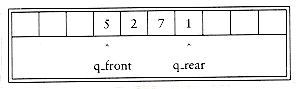
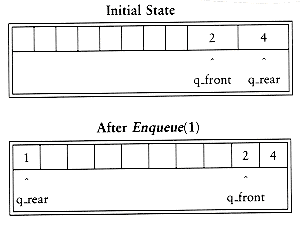
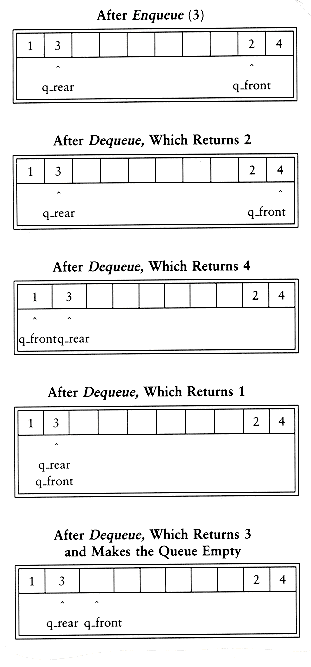
3.4.3. Applications of Queues
struct queue_record
{unsigned int q_max_size; /* Maximum # of elements */
/* until Q is full */
unsigned int q_front;
unsigned int q_rear;
unsigned int q_size; /* Current # of elements in Q */
element_type *q_array;
};
typedef struct queue_record * QUEUE;
Figure 3.57 Type declarations for queue--array implementation
int
is_empty( QUEUE Q )
{return( Q->q_size == 0 );
}
Figure 3.58 Routine to test whether a queue is empty-array implementation
void
make_null ( QUEUE Q )
{Q->q_size = 0;
Q->q_front = 1;
Q->q_rear = 0;
}
Figure 3.59 Routine to make an empty queue-array implementation
unsigned int
succ( unsigned int value, QUEUE Q )
{if( ++value == Q->q_max_size )
value = 0;
return value;
}
void
enqueue( element_type x, QUEUE Q )
{if( is_full( Q ) )
error("Full queue");else
{Q->q_size++;
Q->q_rear = succ( Q->q_rear, Q );
Q->q_array[ Q->q_rear ] = x;
}
}
Figure 3.60 Routines to enqueue-array implementation
Calls to large companies are generally placed on a queue when all operators are busy. In large universities, where resources are limited, students must sign a waiting list if all terminals are occupied. The student who has been at a terminal the longest is forced off first, and the student who has been waiting the longest is the next user to be allowed on.Summary
Exercises
L2 using only the basic list operations.
L2 using only the basic list operations.(x), and computes ((x))p. What is the complexity of your program? Propose at least one alternative solution that could be competitive for some plausible choices of (x) and p./*1*/ for( i=0; i<last_position; i++ )
{/*2*/ j = i + 1;
/*3*/ while( j<last_position )
/*4*/ if( a[i] == a[j]
/*5*/ DELETE(j);
else
/*6*/ j++;
}
Figure 3.61 Routine to remove duplicates from a lists--array implementation
(n log n) comparisons if only comparisons are used. Hint: Look to Chapter 7.(logn) time. (This requires reading Chapter 7.)