The program Unbound presented in this section is a simulation of a calculator used in infix mode: a value, an operator, and then a value are entered and the result display is prompted by the entry of a character " = '' or one that represents another operator. The functions provided are addition ("+"), subtraction ("-"), multiplication ("*"), division ("/"), display ("="), clear the accumulator ("C''), and quit ("Q"). The inclusion of M + (add to memory), M - (subtract from memory), MRC (recover from memory), and MCL (memory clear) are left as a challenge.
The program Unbound is developed in this section, rather than simply described or listed, in order to document the series of design decisions implemented by the program. The logic of Unbound is clarified by developing it in pseudocode and then translating that logic into Pascal.
D.1 The Entry Sequence
A crucial feature of a calculator is that it is fairly robust: mistaken entries do little harm, and that feature should be retained in a simulating program. The possibilities for ambiguous entries are much increased with the use of a terminal keyboard in place of the more restricted calculator keypad. In that spirit, extraneous characters are ignored. The accepted characters are digits 0 -9 and operators ''+'', "-", ''*'', ''/'', '' = '', ''C'', ''Q''. All others are ignored. For example, A17B3 is accepted as 173. For the sake of robustness, division by 0 simply results in 0.
The basic response of the program is designed to deal with entry sequences such as: 24 + 9 =, which results in a display of 33 and the retention of that value in an accumulator (represented by the variable AC). A string of digits that designates a number is terminated by an operator, and so it is (value,operator)-pairs that are accepted by the program. Although an operator terminates the entry of a number, it is the previous operator that usually determines the action. (Operators such as ''C" and ''Q'' are exceptions.) In more detail, if the entering value is X and the result of arithmetic is held in AC, the action of this sequence can be traced as shown in Table D.1.
Table D.1
Entries X NewOp Op AC
--------------------------
C 0
24+ 24 + C 24
9= 9 = + 33
The operation of most calculators is more complex than this example seems to imply. What, for example, is the result of the following entry sequences?
- 24 + 9 =
- 24 + 9 +
24 + +
24 + + =
24 + + + =
The results generated by the program developed here are -15, -15, 24, 48, and 72, respectively. The last of these is not standard, but it is convenient to have each new operator invoke the response of the previous one. If no new X is entered, the AC value is used as X.
D.2 Utility Routines
A procedure Preface is used to initialize variables and provide instructions to the user; Clear is used to set registers such as AC to zero; and Display writes out the value in the accumulator AC. These utility routines are supplemented by arithmetic procedures that act on AC.
The procedure ValueIn that extracts the tokens X and NextOp also returns a Boolean flag NoX to indicate the presence of a numeric value between operators. The command-shell executes the previous operator, Op, in response to the next operator, NextOp. If no X-value is entered withNextOp, then the current value of AC is copied into X. Operators "Q'' and ''C'' require immediate response. When "Q'' is NextOp, it causes immediate termination of the program. When NextOp is ''C'' both AC and X are cleared, and Op is set to "C'' also. When Op is either "C'' or ''='', and an X-value is entered with NextOp, the X-value becomes the new AC value.
The command-shell program that results is:
program UnBound
Preface
DoneFALSE
Op'C'
repeat
ValueIn(X,NoX,NextOp)
if NextOp = 'Q'
then DoneTRUE
else if NextOp = 'C'
then Clear(AC)
Clear(X)
Op'C'
endif
if NoX then XAC endif
case of Op
'=', 'C': Swap {AC with X
'+' :Add(AC,X)
{'-', '*', '/' are similar to '+'}
endcase
endif
OpNextOp
Display
until Done
end {UnBound
The next level of detail is dependent on the implementation of values, and that implementation must allow assignments X 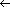 AC and AC
AC and AC 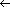 X for unbounded strings of digits. Values need to carry a sign, have leading zeroes suppressed for the sake of efficiency and display, be compared in magnitude (left-to-right for corresponding digits), and be used right-to-left in arithmetic operations. The chosen implementation for AC and X is a pointer to a header of a doubly linked list. Such a list plays the role of a register--a storage location directly associated with computation. For reasons that only become apparent when operations are examined in detail, it is convenient to carry one leading zero and link it to itself. When AC
X for unbounded strings of digits. Values need to carry a sign, have leading zeroes suppressed for the sake of efficiency and display, be compared in magnitude (left-to-right for corresponding digits), and be used right-to-left in arithmetic operations. The chosen implementation for AC and X is a pointer to a header of a doubly linked list. Such a list plays the role of a register--a storage location directly associated with computation. For reasons that only become apparent when operations are examined in detail, it is convenient to carry one leading zero and link it to itself. When AC 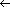 743, the resulting register structure is shown in Figure D.1.
743, the resulting register structure is shown in Figure D.1.

Figure D.1
The Sign field is Boolean, with TRUE corresponding to positive values--making tests involving signs more convenient.
A header such as AC or X can then be initialized by:
procedure NewRegister(R)
NEW(d)
d.Left
d
d.Value
0
d.Right
NIL
NEW(R)
R.First
d
R.Last
d
R.Sign
TRUE
R.Count
0
end {NewRegisterSetting an initialized register back to zero can be even simpler:
procedure Clear(R)
R.Last
R
.First
R.Count
0
R.Sign
TRUE
end {ClearThis procedure, however, does not recover the (possibly many) digit nodes that were in the register R. A more practical version of Clear is:
procedure Clear(R)
pR
.Last
qp
.Left
while pR
.First do
DISPOSE(p)
pq
qp
.Left
endwhile
p.Right
NIL
R.Last
p
R.Count
0
R.Sign
TRUE
end {ClearThe speed of arithmetic operations is directly dependent on the number of digits involved, and so removal of duplicate leading zeroes is an essential part of housekeeping:
procedure Compact(R)
pR
.First
qp
.Right
while qNIL do
if q.Value
0
then exit
else tq
.Right
DISPOSE(q)
R.Count
R
.Count - 1
P.Right
t
qt
if tNIL
then t.Left
p endif
endif
endwhile
if R.Count = 0 then R
.Last
R
.First endif
end {CompactNote: The pair of tests at the top of this loop require a fair amount of modification when implemented in Pascal because the condition:
(qNIL) AND (q
.Value
0)
is risky. A more direct translation results from the use of GOTO to implement exit.
On the principle of "never trust the user," compaction is included as the last action in ValueIn.
The input-token generator ValueIn is:
procedure ValueIn(X,NoX,NextOp)
NoXTRUE
Clear(X)
Read(ch)
while NOT (ch IN OperatorSet) do
if ch IN [0..9]
then NoXFALSE
NEW(d)
d.Right
NIL
d.Value
ORD(ch) - ORD('0')
d.Left
X
.Last
X.Last
.Right
d
X.Last
d
X.Count
X
.Count + 1
endif
Read(ch)
endwhile
NextOpch
Compact(X)
end {ValueIn
D.3 Arithmetic Operations
The fundamental operation of arithmetic is addition, but it becomes subtraction when the signs of the operands differ. When done by hand, the value of smaller magnitude is subtracted from the other. One simple approach to addition is based on two steps:
1. Compare AC and X and switch them if necessary to insure that 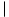 AC
AC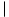
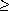
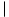 X
X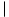 .
.
2. If the signs agree, then add magnitudes with procedure Carry; otherwise, subtract the magnitudes with procedure Borrow.
The resulting logic is:
procedure Add(X)
RLargerOf(AC,X)
if R = X
then XAC
ACR
endif
if X.Count = 0 then return endif
if AC.Sign = X
.Sign
then Carry(AC,X)
else Borrow(AC,X)
endif
end {Add
function LargerOf(AC,X) {O(n) Assumes compacted operands
if AC.Count > X
.Count then return AC endif
if X.Count > AC
.Count then return X endif
kAC
.Count
pACAC
.First
.Right
pXX
.First
.Right
while k > 0 do
if pAC.Value > pX
.Value then return AC endif
if pAC.Value < pX
.Value then return X endif
pACpAC
.Right
pXpX
.Right
kk - 1
endwhile
return AC {X = AC
end {LargerOfNote: The returns are replaced by a nest of IF-statements in Pascal. Add, Subtract, Multiply, and Divide all may switch X and AC to avoid copying a long list of digits, and so X is a VAR parameter in the Pascal implementation.
The last carry operation can create a new digit (as in 997 + 18), which is signaled by a carry after the last X-digit has been added to AC. The last borrow can propagate to the left (as in 10003 - 4), but that can be handled by continuing to subtract the leading zero node, X  .First. With these problems recognized:
.First. With these problems recognized:
procedure Carry(X)
pACAC
.Last
pXX
.Last
Over0
for k = 1 to AC.Count do
SumpAC
.Value + pX
.Value + Over
if Sum > 9
then Over1
pAC.Value
Sum - 10
else Over0
pAC.Value
Sum
endif
pACpAC
.Left
pXpX
.Left
next k
if Over > 0
then NEW(d)
d.Right
pAC
.Right
d.Left
pAC
pAC.Right
.Left
d
pAC.Right
d
d.Value
Over
AC.Count
AC
.Count + 1
endif
end {Carry
procedure Borrow
pACAC
.Last
pXX
.Last
Loan0
for k = 1 to AC.Count do
DifferencepAC
.Value - pX
.Value - Loan
if Difference < 0
then Loan1
pAC.Value
Difference + 10
else Loan0
pAC.Value
Difference
endif
pACpAC
.Left
pXpX
.Left
next k
Compact(AC)
end {BorrowWith Add complete, subtraction becomes very simple:
procedure Subtract(X)
X.Sign
NOT X
.Sign
Add(X)
end {Subtract
Multiplication can be done by repeated addition in two ways: 47  31 = (47 + 47 + . . . + 47, 31 times) and 47
31 = (47 + 47 + . . . + 47, 31 times) and 47  31 = (47 + 3
31 = (47 + 3  470). The latter approach is used here. It will square 2 raised to the 96th power in a few seconds on an inexpensive microcomputer (after compilation by a $30 Pascal compiler). This operation would take years by repeated addition.
470). The latter approach is used here. It will square 2 raised to the 96th power in a few seconds on an inexpensive microcomputer (after compilation by a $30 Pascal compiler). This operation would take years by repeated addition.
Several values are involved in multiplication: the original operands X and AC, the shifting values Y (such as 47, 470, . . . ), the product of a digit of X with a Y, say M, and the running sum of these products. AC supplies the original Y and then may contain the running sum. The product sign must be determined but not affect the use of Add to multiply magnitudes, and a value with a minimal number of digits should be used to control the multiplication loop. This housekeeping is done by:
procedure SetUp
YAC
NewRegister(AC)
New Register(M)
RLargerOf(Y,X)
if R = X
then XY
YR
endif
NewSign(Y
.Sign = X
.Sign)
X.Sign
TRUE
Y.Sign
TRUE
Clear(AC)
end {SetUpA routine is needed to shift successive products one digit to the left. One approach is to shift Y:
procedure ShiftLeft(Y)
NEW(d)
d.Value
O
d.Right
NIL
d.Left
Y
.Last
Y.Count
Y
.Count + 1
Y.Last
.Right
d
Y.Last
d
end {ShiftLeftMultiplication then can be done with:
procedure Multiply(X)
SetUp
if X.Count = 0 then return endif
pXX
.Last
for j = 1 to X.Count do
Over0
MakeCopy(M,Y)
pMM
.Last
pXX
.Last
vpX
.Value
for k = 1 to M.Count do
ProductpM
.Value * v + Over
pM.Value
Product MOD 10
OverProduct DIV 10
pMpM
.Left
next k
if Over > 0
then NEW(d)
d.Right
pM
.Right
d.Left
pM
pM.Right
.Left
d
pM.Right
d
M.Count
M
.Count + 1
d.Value
Over
endif
Add(AC,M)
ShiftLeft(Y)
pXpX
.Left
next j
AC.Sign
NewSign
Clear(Y)
Clear(M)
end {MultiplyDivision by repeated subtraction is as slow as multiplication by repeated addition, but the alternative algorithm used by fifth graders is much more complex than repeated subtraction. For contrast with multiplication, a version of repeated subtraction is applied here: the divisor is added to itself until it is larger than the dividend. Each such addition is paired with an increment of the result.
Auxiliary registers are used as they are for multiplication and destroyed on exit from Divide. The initialization is:
procedure Prolog
NewSign(AC
.Sign = X
.Sign)
AC.Sign
TRUE
X.Sign
TRUE
DAC
NewRegister(AC)
NewRegister(R)
NewRegister(S)
end {PrologThe resulting divide logic is:
procedure Divide(X)
if X.Count = 0
then Clear(AC)
return
endif
Prolog
MakeCopy(S,X)
MakeCopy(AC,One)
RLargerOf(D,S)
while R = D do
Carry(AC,One)
Carry(S,X)
RLargerOf(D,S)
endwhile
Borrow(AC,One)
AC.Sign
NewSign
Clear(D)
Clear(S)
end {DivideA listing of a Pascal program that results from this design follows:
PROGRAM UnBound (InPut,OutPut);
TYPE Digit =DigitNode;
Register =RegisterNode;
DigitNode = RECORD
Value : 0 . . 9;
Left : Digit;
Right : Digit
END;
RegisterNode = RECORD
Sign : BOOLEAN;
Count : INTEGER;
First : Digit;
Last : Digit
END;
VAR Op ,NextOP : CHAR;
NoX,Done : BOOLEAN;
One,X,AC : Register;
OperatorSet : SET OF CHAR;
Numeric : SET OF CHAR;
{ }
PROCEDURE Display (AC : Register);
VAR pAC : Digit;
k : INTEGER;
BEGIN
Write1n;
pAC := AC.First;
IF NOT (AC. Sign) THEN Write('-');
FOR k := 1 TO (AC. Count + 1) DO BEGIN
Write(pAC.Value);
pAC := pAC. Right
END;
Write1n
END {Display};
{ }
PROCEDURE NewRegister(VAR R : Register);
VAR d : Digit;
BEGIN
NEW(d);
d.Left := d;
d.Value := 0;
d.Right := NIL;
NEW(R);
R.First := d;
R.Last := d;
R.Sign := TRUE;
R.Count := 0
END {NewRegister};
{ }
PROCEDURE Clear (VAR R : Register);
VAR p , q : Digit;
BEGIN
p := R.Last;
q := P.Left;
WHILE (p <> R.First) DO BEGIN
DISPOSE(p);
p := q;
q := p.Left
END;
R.Last := p;
R.Count := 0;
P.Right := NIL;
R.Sign := TRUE
END {Clear};
{ }
PROCEDURE MakeOne(VAR One : Register);
VAR d : Digit;
BEGIN
NewRegister(One);
NEW(d);
d.Value := 1;
d.Left := One
.First;
d.Right := NIL;
One.First
.Right := d;
One.Last := d;
One.Count := 1
END {MakeOne};
{ }
PROCEDURE Preface;
BEGIN
Write1n('This program simulates a calculator that');
Write1n('allows unbounded integers. Enter values');
Write1n('followed by operators. The accepted operators');
Write1n('are: +,-,*,/,=,C (for clear),Q (for quit).');
NewRegister(AC);
NewRegister(X);
MakeOne(One);
Numeric := ['0'..'9'];
OperatorSet := ['+','-','*','/','=','C','Q']
END {Preface};
{ }
PROCEDURE Compact(VAR R : Register);
VAR p, q, t : Digit;
BEGIN
p := R.First;
q := p.Right;
IF (q <> NIL) THEN IF (q.Value <> 0) THEN q:= NIL;
WHILE (q <> NIL) DO BEGIN
t := q.Right;
DISPOSE(q);
R.Count := R
.Count - 1;
P.Right := t;
q := t;
IF (t <> NIL)
THEN BEGIN
t.Left := p;
IF (t.Value <> 0) THEN q := NIL
END
END;
IF (R.Count = 0) THEN R
.Last := R
.First
END {Compact};
{ }
PROCEDURE ValueIn(VAR X : Register; VAR NoX : BOOLEAN;
VAR NextOP : CHAR);
VAR ch : CHAR;
d : Digit;
BEGIN
NoX := TRUE;
Clear(X);
Read(ch);
WHILE NOT (ch IN OperatorSet)
DO BEGIN
IF (ch IN Numeric)
THEN BEGIN
NoX := FALSE;
NEW(d);
d.Right := NIL;
d.Value := ORD(ch) - ORD('0');
d.Left := X
.Last;
X.Last
.Right := d;
X.Last := d;
X.Count := X
.Count + 1
END;
Read(ch)
END;
NextOp := ch;
Compact(X)
END {ValueIn};
{ }
FUNCTION LargerOf(AC,X : Register) : Register;
VAR K : INTEGER;
pAC,pX : Digit;
BEGIN
LargerOf := AC;
IF (AC.Count <= X
.Count) THEN
IF (AC.Count < X
.Count)
THEN LargerOf := X
ELSE BEGIN
k := AC.Count;
pAC := AC.First
.Right;
pX := X.First
.Right;
WHILE (k > 0) DO
IF (pAC.Value < = pX
.Value)
THEN IF (pAC.Value < pX
.Value)
THEN BEGIN
LargerOf := X;
K := O
END
ELSE BEGIN
pAC := pAC.Right;
pX := pX.Right;
k := k - 1
END
ELSE k := O
END;
END {LargerOf};
{ }
PROCEDURE MakeCopy(VAR M : Register; Y : Register);
VAR d,pY : Digit;
k : INTEGER;
BEGIN
Clear(M);
IF (Y.Count > 0) THEN BEGIN
pY := Y.First
.Right;
FOR k := 1 TO Y.Count DO BEGIN
NEW(d);
d.Right := NIL;
d.Value := PY
.Value;
pY := pY.Right;
d.Left := M
.Last;
M.Last
.Right := d;
M.Last := d
END;
M.Count := Y
.Count;
END
END {MakeCopy};
{ }
PROCEDURE Carry(VAR AC : Register; X : Register);
VAR pAC, pX, d : Digit;
k,Sum, Over : INTEGER;
BEGIN
pAC := AC.Last;
pX := X.Last;
Over := 0;
FOR K := 1 TO AC.Count DO BEGIN
Sum := pAC.Value + pX
.Value + Over;
IF (Sum > 9)
THEN BEGIN
Over := 1;
pAC.Value := Sum - 10
END
ELSE BEGIN
Over := 0;
pAC.Value := Sum
END;
pAC := pAC.Left;
pX := pX.Left
END;
IF (Over > 0)
THEN BEGIN
NEW(d);
d.Right := pAC
.Right;
d.Left := pAC;
pAC.Right
.Left := d;
pAC.Right := d;
d.Value := Over;
AC.Count := AC
.Count + 1
END
END {Carry};
{ }
PROCEDURE Borrow(VAR AC: Register; X: Register);
VAR pAC,pX: Digit;
k,Loan,Difference: INTEGER;
BEGIN
pAC := AC.Last;
pX := X.Last;
Loan := 0;
FOR k := 1 TO AC.Count DO BEGIN
Difference := pAC.Value - pX
.Value - Loan;
IF (Difference < 0)
THEN BEGIN
Loan := 1;
pAC.Value := Difference + 10
END
ELSE BEGIN
Loan := 0;
pAC.Value := Difference
END;
pAC := pAC.Left;
pX := pX.Left
END;
Compact(AC)
END {Borrow};
{ }
PROCEDURE Add(VAR AC: Register; VAR X : Register);
VAR R: Register;
BEGIN {X is VAR as AC may swap with it.}
R := LargerOf(AC,X);
IF (R = X)
THEN BEGIN
X := AC;
AC := R
END;
IF (X.Count <>0)
THEN IF (AC.Sign = X
.Sign)
THEN Carry(AC,X)
ELSE Borrow(AC,X)
END {Add};
{ }
PROCEDURE Subtract(VAR AC: Register; VAR X: Register);
BEGIN
X.Sign := NOT X
.Sign;
Add(AC,X)
END {Subtract};
{ }
PROCEDURE Multiply (VAR AC: Register; VAR X: Register);
VAR pM,pX,d: Digit;
M,Y : Register;
v,k,j,Over,Product: INTEGER;
NewSign: BOOLEAN;
{ }
PROCEDURE SetUp;
VAR R: Register;
BEGIN
Y := AC;
NewRegister(AC);
NewRegister(M);
R := LargerOf( Y,X);
IF (R = X)
THEN BEGIN
X := Y;
Y := R
END;
NewSign := (Y.Sign = X
.Sign);
X.Sign := TRUE;
Y.Sign := TRUE;
Clear(AC)
END {SetUp};
{ }
PROCEDURE ShiftLeft(VAR Y: Register);
VAR d: Digit;
BEGIN
NEW (d);
d.Value := 0;
d.Right := NIL;
d.Left := Y
.Last;
Y.Count := Y
.Count + 1;
Y.Last
.Right := d;
Y.Last := d
END {ShiftLeft};
{ }
BEGIN {Multiply}
SetUp;
IF (X.Count <> 0)
THEN BEGIN
pX := X.Last;
FOR j := 1 TO X.Count DO BEGIN
Over := 0;
MakeCopy(M,Y);
pM := M.Last;
v := pX.Value;
FOR k := 1 TO M.Count DO BEGIN
Product:=pM.Value* v + Over;
pM.Value := Product MOD 10;
Over := Product DIV 10;
pM := pM.Left
END;
IF (Over > 0)
THEN BEGIN
NEW (d);
d.Right := pM
.Right;
d.Left := pM;
pM.Right
.Left := d;
pM.Right := d;
M.Count := M
.Count + 1;
d.Value := Over
END;
Add(AC,M);
ShiftLeft(Y);
pX := pX.Left
END;
AC.Sign := NewSign;
Clear(Y);
Clear(M)
END
END {Multiply};
{ }
PROCEDURE Divide(VAR AC: Register; VAR X: Register);
VAR NewSign: BOOLEAN;
D,R,S : Register;
{ }
PROCEDURE Prolog;
BEGIN
NewSign := (AC.Sign = X
.Sign);
AC.Sign := TRUE;
X.Sign := TRUE;
D := AC;
NewRegister(AC);
NewRegister(R);
NewRegister(S)
END {Prolog};
{ }
BEGIN {Divide}
IF (X.Count = 0)
THEN Clear(AC)
ELSE BEGIN
Prolog;
MakeCopy(S,X);
MakeCopy(AC,One);
R := LargerOf(D,S);
WHILE (R = D) DO BEGIN
Carry(AC,One);
Carry(S,X);
R := LargerOf(D,S)
END;
Borrow(AC,One);
AC.Sign := NewSign;
Clear(D); Clear(S)
END
END {Divide};
{ }
PROCEDURE Swap;
VAR R: Register;
BEGIN
R := AC;
AC := X;
X := R
END {Swap};
{**
**}
BEGIN {UnBound}
Preface;
Done := FALSE;
Op := 'C';
REPEAT
ValueIn(X,NoX,NextOp);
IF (NextOp = 'Q')
THEN Done = TRUE
ELSE BEGIN
IF (NextOp = 'C')
THEN BEGIN
Clear(X); Clear(AC);
Op :='C'
END;
IF NoX THEN MakeCopy(X,AC);
CASE Op OF
'C' : Swap; {AC with X}
'=' : Swap;
'+' : Add(AC,X);
'-' : Subtract(AC,X);
'*' : Multiply(AC,X);
'/' : Divide(AC,X)
END
END;
Op := NextOp;
Display(AC)
UNTIL Done
END {UnBound}.


