



A maze of passages is (topologically) equivalent to a rectangular array of block positions, some occupied and some forming passages because they are not occupied. A very simple example is shown in Figure H.1 .

Such an array of blocks corresponds to an array of values. For example,
M[I,J] = 1
may correspond to an open (unoccupied) block and M[I,J] = 0 to a closed (occupied) block. The maze of Figure H.1 is then represented by:
M 1 2 3 4 5 6 7 8
1 0 0 0 1 0 0 0 0
2 0 1 1 1 0 0 1 0
3 0 1 0 1 0 0 1 0
4 0 1 0 1 1 1 1 0
5 0 1 0 0 0 0 1 1
6 0 1 1 0 1 1 1 0
7 0 0 0 0 1 0 0 0
8 0 0 0 0 1 0 0 0
While searching such a table for a passageway from an entrance position (R,C) to an exit position, it is convenient to mark positions (I,J) already visited by the assignment M[I,J]  2. An algorithm that searches the table form of the maze for passageways from an entrance to another exit can be designed around a stack of positions:
2. An algorithm that searches the table form of the maze for passageways from an entrance to another exit can be designed around a stack of positions:
Push (R,C) and set M[R,C] to 2. The pair (R,C) is the current position.
repeat
1. Test the four positions adjacent to (R,C) (on the North, East, South, and West). For a position (I,J) for which M[I,J] = 1, push (I,J) and set M[I,J] to 2. If no adjacent position is open, then delete (I,J) and set M[R,C] to 0 to indicate that the current position leads nowhere.
2. (R,C)  TopValue
TopValue
until (R,C) is a border position.
If the final (R,C) is the initial entrance pair, then the maze has no other exit because all branch-paths from all blocks accessible from the start block have been tried. The contents of the stack define a path from entrance to exit. If adjacent positions are tested in clockwise order, a trace of the first few loop iterations for the example maze are:
(R,C) STACK
(1,4) (1,4)
(1,4) (1,4) (2,4)
(2,4) (1,4) (2,4) (3,4) (2,3)
(2,3) (1,4) (2,4) (3,4) (2,3) (2,2)
(2,2) (1,4) (2.4) (3,4) (2,3) (2,2) (3,2)
(3,2) (l,4) (2,4) (3,4) (2,3) (2,2) (3,2) (4,2)
(4,2) (l,4) (2,4) (3,4) (2,3) (2,2) (3,2) (4,2) (5,2)
(5,2) (1,4) (2,4) (3,4) (2,3) (2,2) (3,2) (4,2) (5,2) (6,2)
(4,2) (1,4) (2,4) (3,4) (2,3) (2,2) (3,2) (4,2) (5,2) (6,2) (6,3)
(4,2) (1,4) (2,4) (3,4) (2,3) (2,2) (3,2) (4,2) (5,2) (6,2)
.
.
.
Exercise EH.1 is appropriate at this point.
From this point, the algorithm will backtrack, erasing false passages as it goes.
An appropriate data structure for the stack is an array of records, each containing a pair of indices. The entrance pair, for instance, may be entered as integers I0 and J0 and placed in a position record Start by: Start.Row  I0, Start.Column
I0, Start.Column  J0.
J0.
The remaining technical problem is the search of positions adjacent to the current one. The positions adjacent to pair (R,C) are:
(I - 1,J), (I,J + 1), (I + 1,J), and (I,J - 1)
These can be derived by adding pairs (-1,0), (0,1), (1,0), and (0,-1) to (R,C). For convenience in looping through the four possibilities, they can be stored in an array of pairs, shown in Figure H.2.
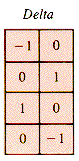
An implementation of this scheme requires that (I,J) + Delta(k) fall within the table for any (I,J) in the maze. Consequently, extra rows of zeros should be provided at each edge of the maze table (in rows 0 and RowMax + 1, columns 0 and ColumnMax + 1).
The algorithm, configured as a procedure to which the maze-table and entrance data are passed is:
procedure Mouse(Start,M,RowMax,ColumnMax)
Push(Start)
RStart.Row
CStart.Column
M[R,C]2
repeat
DeadEndTRUE
for k1 to 4 do
IR + Delta[k].Row
JC + Delta[k].Column
if M[I,J] = 1
then Test.RowI
Test.ColumnJ
Push(Test)
M[I,J]2
DeadEndFALSE
endif
next k
if DeadEnd
then Delete
M[I,J]0
endif
PositionTopValue
RPosition.Row
CPosition.Column
if R = 0 OR R = RowMax
OR C = 0 OR C = ColumnMax
then DoneTRUE
else DoneFALSE
endif
until Done
end {Mouse
Exercises immediate applications of the text material
EH.1 Complete the trace of the example maze.
Problems not immediate, but requiring no major extensions of the text
PH.1 Mouse can maintain a second stack of branch points--blocks with two or more adjacent open blocks. This stack can be used to find all the paths from entrance to other exits. How?
Programs for trying it yourself
PGH.1 Implement Mouse within a program.
Problems
Programs