Pursuit of the terms "well enough" and "experimental" in the definition given lead to a vast but amorphous literature and practice. The practice is an art of importance that increases with the power of computing, yet the literature contains no decisive entry point. The intent of this section is to provide a program that is a framework for the study of a simple system and hence a window onto one part of the practice of simulation.
A professionally developed simulation program is designed for a real system on the basis of carefully collected and analyzed data. The worth of a thoughtfully determined goal is balanced against the (sometimes considerable) cost of writing and using it. The assumptions built into the system as a program model are checked for validity against the real world, and the behavior of the program is verified to be that of the assumed system. Many systems that are simulated involve random behavior, imitated by a program model, and so experiments are run on the simulation program. These experiments and the analysis of their results are both developed with statistical care.
This section is only intended to provide an example of the possibilities and a minimal framework for experiment. It is only the program portion of a simulation process that appears here.
K.1 The Customs Station
An airport customs station receives arriving passengers at a check-in counter. Passengers wait until one of several clerks is available to serve them. They are served in a time that has an (essentially) normal distribution about a mean. (The distribution cannot actually be normal, since negative service times are not possible, and they are discarded when drawn from it. Such a distribution is called truncated normal.) If the passengers have prepaid their customs tax, they depart the counter. If they have not, they are sent to a tax station, where they wait in a tax queue until served by one of several tax agents. They are served at the tax counter in time that has an exponential distribution. On exit from the tax counter, a passenger rejoins the customs-clerk queue but, when reaching a clerk a second time, is serviced in a constant time. A schematic of this system is shown in Figure K.1.
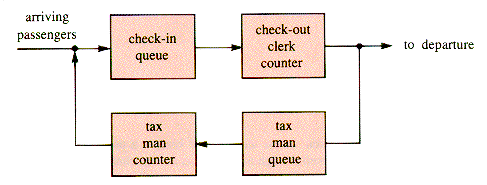
Figure K.1
This system looks deceptively simple, but the events that occur in it are several:
Arrival: A passenger arrives at the station from outside the station "universe." If there is a free clerk, the passenger is scheduled for check-in immediately; otherwise, the passenger waits in the clerk queue.
Check-in: A passenger is simply scheduled for checkout at a time that is "now" plus a check-out service time. This becomes the DoTime of the passenger--the time at which his or her event is to be done.
Check-out: A passenger completes service by a clerk and either departs the station or is sent to the tax counter. If there is a free tax agent, the passenger is scheduled for Tax-in immediately and otherwise waits in the tax queue.
Tax-in: A passenger is scheduled for Tax-out, at a DoTime value determined by "now" plus the tax service-time distribution.
Tax-out: A passenger completes service by a tax agent and, if there is an available clerk, is sent to the clerk counter again, to Check-in, in effect. If no clerk is available, the passenger waits in the clerk queue.
These are processes, represented by procedures in a simulation program written in a language such as Pascal. These processes occur at times determined by random distributions and so occur in a random sequence. At any time, the next process to be executed may be any one of them; and several can occur at the same time. A procedural simulation program moves from event to event, each a process acting on a passenger. The program must be able to schedule the next event and handle events one at a time. Simulation time is tracked by a "clock" that is advanced to the scheduled time of the current event, the DoTime of the customer being processed. The clock is not advanced when a completed event is followed by a "simultaneous" event, scheduled at the current clock time.
A common simulation technique is to have one event in a distribution stream (such as the arrival stream) schedule the next one. The process that manages the arrival of passenger I fetches the next random interarrival time from the arrival stream, say ia. If the system clock is Clock, then the arrival of the next passenger, say J, occurs at time: Clock + ia. The arrival of the passenger after J is determined at the time of arrival of J, when process Arrival acts on J. Scheduling of processes can be done by a generalization of this kind of scheduling of events in a distribution stream, as indicated by the process descriptions.
Passengers spend most of their time outside of processes. A passenger who has just been checked in at one time will be processed again at his (or her) scheduled check-out time. A number of processes may be active between these times, and several events may occur at the check-out time. The program representation of a passenger (normally a record) waits somewhere when not being processed. This somewhere is an event queue--a priority queue of passenger records not currently in process. The priority involved is the time of the next event that is to happen to the passenger. Hence a passenger (record) is scheduled for one event after another until it departs the system, and it waits its turn on the event queue. The priorities may be determined by simply keeping the records of the event queue sorted by the DoTime (next-event time) of the passenger records in it.
The scheme outlined above for managing processes (events) and entities (passengers) advances the simulation clock from one scheduled event to the next in an unpredictable but very organized manner. (The next event being the DoTime of the record at the front of the priority queue.) This is called discrete-event simulation, although it applies strictly only to the program portion of a simulation. It is the technique chosen for the simulation program Airport developed for the airport customs station in the remainder of this section.
K.2 The Event-Cycle Level of Airport
The program level that corresponds to a command-shell in the management of a simple discrete-event simulation is an event-cycle level. At this level, control passes from one process to another, driven by the scheduling of events for entities (passenger records in this case).
The number of passenger entities in the station at any (simulation) time is ultimately determined by the interaction of four distributions: arrival, check-out service, tax service, and the uniform distribution used to decide if a passenger has prepaid the customs tax. The interaction of these is complex for the system as a whole, but for an individual passenger it is relatively simple: a passenger progresses in stages. The stages are each associated with a particular procedure:
Stage 1. Birth: The passenger arrives, an event managed by procedure Arrival. Arrival marks the record of passenger P as stage 2 so that its next stage will be recognized by any process that handles it. Arrival assigns P to an idle clerk if there is one, and schedules CheckIn at the current time. "Scheduled" means placement in the sorted list EventQueue. If no clerk is available, P is placed in a waiting line, ClerkQueue, and no event is scheduled by Arrival for P. Arrival also schedules the next arrival, drawing from the interarrival distribution to do so.
Stage 2. Initial check-in: An idle clerk is put to work on passenger P by procedure Check-in. In effect, P is scheduled for check-out at the current time Clock plus an increment drawn from a truncated normal distribution that represents clerk service times.
Stage 3. Initial check-out: The initial check-out service by a clerk is complete. The managing procedure, CheckOut, draws a uniform variate to decide whether to send P to Depart (where the passenger record will die--leave the system) or to the tax counter. If P is to go to the tax counter, the record is marked stage 4 and scheduled for processing by TaxIn at the current time Clock if there is a tax agent available. If no tax agent is available, P is placed in the waiting line TaxQueue. Since check-out frees a clerk, if ClerkQueue is not empty a passenger is removed from it with the queueing discipline FIFO (first-in-first-out): it is a pure queue. CheckOut does not make the decision to process this newly freed passenger, however, but simply schedules the processing.
Stage 4. Tax-counter check-in: Procedure TaxIn draws a service time for P from a (truncated) exponential distribution and schedules completion of tax service for P at that increment plus Clock. The correct routing of P is insured by marking the record stage 5.
Stage 5. Tax-counter check-out: Procedure TaxOut schedules P for CheckIn at the current Clock if there are idle clerks; otherwise, P is placed in ClerkQueue. Routing is insured by marking P as stage 6. Since TaxOut frees a tax agent, if TaxQueue is not empty, a passenger is retrieved from it--with the FIFO queueing discipline--and scheduled.
Stage 6. After-tax check-in: This is managed by CheckIn and differs from stage 2 in that a constant increment PaidTime is added to Clock to form the DoTime of the check-out event for P. Stage 7 marking routes P back to CheckOut.
Stage 7. After-tax check-out: This is managed by CheckOut and leads automatically to death--departure from the system.
Passengers are placed in EventQueue by procedure Schedule and removed from it by procedure NextEvent. Procedure NextEvent deals with a subtlety that is typical of simulation programming: more than one passenger can be scheduled for check-in with the same idle clerk or tax agent. This is a (deliberate) artifact of the program design; but alternate designs tend to lead to other timing problems, and some can create bugs that are not easy to detect. As given here, NextEvent simply reschedules a passenger for whom there is no idle server and chooses another passenger.
EventQueue can never be empty because the last arrival always schedules the next, and that (unborn) passenger cannot be scheduled for any process except Arrival, which then schedules another arrival. . . .
The division of labor among the procedures is somewhat arbitrary. In particular, the decision to schedule P or place the record in a waiting line ClerkQueue (and TaxQueue) can be moved to CheckIn (and TaxIn). With that change, CheckIn, CheckOut, and ClerkQueue form a unit that communicates with the other processes principally by way of the action of Schedule and NextEvent on EventQueue. Procedures TaxIn, TaxOut, and waiting line TaxQueue form a similar tax unit. The program presented in this section leaves them as described, and the alternative design is suggested as a programming project in PJK.5. (The change simplifies NextEvent.)
In various forms, the ability to package procedures, data structures, and persistent variables confined within a unit, and to spawn copies of a unit as a type has been incorporated into languages such as Simula, Ada, and specifically simulation languages. Such languages would be an improvement on Pascal for writing simulation programs if they were not so complex themselves. A principle of the conservation of complexity seems to be at work for simulations.
With the procedures roughed out, the event-cycle level of Airport becomes:
The last and most-abused stage of a simulation is the gathering and interpretation of data generated by it. Statistical techniques of all levels may be brought to bear on simulation data, as long as it is recognized that the data derives from a model and not the actual system.
The generation of pseudorandom numbers and choice of distributions has attracted a great deal of study but perhaps not always enough in practice. It is common to make repeated runs of a simulation program and determine the mean and standard deviation of both single-run results and results from a sequence of runs. Those results are the measurement of the interaction of a model with approximations of random number sequences.
Even elementary statistics lies outside the scope of this book, and so the goal of Airport is simply to provide data on the mean response time of the model. The amount of (simulation) time spent in the system by a departing passenger is the difference between Clock values at arrival and departure. These times, and the times of occurrence for other stages, are kept in an array Stage[1 . . 7] in the passenger record. They are updated by the procedures that process a passenger at each stage. The only additional information that is gathered by Airport is the state of the system: the queue lengths and the number of idle servers. The intent here is to provide a framework that may be extended in programming projects as desired.
The data provided by Airport is enough to experimentally explore the relationship between the mean times of the distributions, the numbers of clerks and tax agents, and the response time. The experimental space for exploring response time has eight dimensions if the standard deviation of the normal distribution for clerk service is taken into account.
When making short runs, the initial conditions of the queues and the initially all-idle servers bias the results. Suggested solutions are long runs, program modification to allow a "warm start," or a limiting process. This is a universal problem in the interpretation of simulation results, with no single general solution.
Projects for fun; for serious students
PJK.1 With the choices MeanA = 1.0, Mu = 3.0, Sigma = 1.0, MeanT = 2.0, PaidTime = 1.0, and NotPaid = 0.5, determine an optimal balance of clerks and tax agents. The trade-off is to be that two minutes of additional mean response time is as costly in customer-relations as a clerk or tax agent is in money.
PJK.2 Modify Airport so that it allows an initial run to reach equilibrium (perhaps) before data-gathering begins. The warm start is to be followed by a run in segments, as before.
PJK.3 Modify Airport so that it reports the mean queue-lengths of EventQueue, ClerkQueue, and TaxQueue.
PJK.4 Modify Airport so that it reports the utilization of its resources: what fraction of the time are how many clerks and tax agents busy? The output should be a plot of time against number busy (a histogram) for each type of server.
PJK.5 Modify Airport so that the decision to schedule a passenger or to place the record in a waiting line is included in CheckIn and TaxIn.
program AirPort
Clock
 0
0Preface
RunAgain(HowLong)
while HowLong do
OverTime
 Now + HowLong
Now + HowLongwhile Now < OverTime do
p
 NextEvent(EventQueue)
NextEvent(EventQueue)case of p
 .WhatStage
.WhatStage1 : Arrival(p)
2,6 : CheckIn(p)
3,7 : CheckOut(p)
4 : TaxIn(p)
5 : TaxOut(p)
endcase
endwhile
RunAgain(HowLong)
endwhile
end {AirportK.3 The Gathering of Data
Projects
K.4 The Program Airport
PROGRAM Airport (Input, Output);
TYPE Person =
 Entity;
Entity;Entity = RECORD
What Stage : 0 . .7;
Stage : ARRAY[1 . . 7] OF INTEGER;
DoTime : INTEGER;
Link : Person;
id : INTEGER
END;
WaitingLine = RECORD
Front : Person;
Rear : Person
END;
VAR Passenger : Person;
EventQueue : Person;
p : Person;
ClerkQueue : WaitingLine;
TaxQueue : WaitingLine;
EQL,CQL,TQL : INTEGER;
ResponseSum : INTEGER;
IdleTaxMen : INTEGER;
IdleClerks : INTEGER;
Departures : INTEGER;
Arrivals : INTEGER;
OverTime : INTEGER;
PaidTime : INTEGER;
HowLong : INTEGER;
Seed : INTEGER;
Clock : INTEGER;
Sigma,Mu : REAL;
NotPaid : REAL;
MeanA : REAL;
MeanT : REAL;
{ }FUNCTION Random(VAR Seed : INTEGER) : REAL;
CONST Multiplier = 13077;
Increment = 6925;
Modulus = 32767;
BEGIN {A version that works well on a KayPro whencompiled with JRT Pascal.}
Seed := (Multiplier * Seed + Increment) MOD Modulus;
Random := (Seed/Modulus + 1.0) /2.0
END {Random};{ }FUNCTION Normal : INTEGER;
VAR z : REAL;
k,N : INTEGER;
BEGIN
REPEAT
z := 0;
FOR k := 1 TO 12 DO z := z + Random(Seed);
z := z - 6.0;
N := TRUNC(0.5 + Sigma * z + Mu)
UNTIL (N > 0);
Normal := N
END {Normal};{ }FUNCTION LN(X : REAL) : REAL; EXTERN;
{ }FUNCTION Expon(OneOver : REAL) : INTEGER;
VAR k,ia : INTEGER;
BEGIN
REPEAT
ia := TRUNC(0 . 5 - LN(Random(Seed)) * OneOver)
UNTIL (ia > 0);
Expon : = ia
END {Expon};{ }PROCEDURE Report(p : Person);
VAR k : INTEGER;
BEGIN {Used for debugging}Writeln; {of modifications}Writeln (EQL,CQL,TQL);
Writeln ('Passenger' ,p  . id);
. id);Writeln ('Stage ',p  .WhatStage);
.WhatStage);Write ('Stage history : ');FOR k := 1 TO 7 DO Write(p
 .Stage[k]/60.0 : 7 : 2);
.Stage[k]/60.0 : 7 : 2);Writeln; Writeln
END {Report};{ }FUNCTION NewPassenger : Person;
VAR p : Person;
k : INTEGER;
BEGIN
NEW(p);
p
 .WhatStage := 1;
.WhatStage := 1;p
 .DoTime := Clock + Expon(MeanA);
.DoTime := Clock + Expon(MeanA);FOR k := 1 TO 7 DO p
 .Stage[k] := 0;
.Stage[k] := 0;p
 .id := Arrivals + 1;
.id := Arrivals + 1;NewPassenger := p
END {NewPassenger};{ }PROCEDURE Schedule(VAR p : Person);
VAR q,r : Person;
BEGIN
r := EventQueue;
IF (r = NIL)
THEN BEGIN
p
 .Link := NIL;
.Link := NIL;EventQueue := p
END
ELSE IF (p
 .DoTime < r
.DoTime < r  .DoTime)
.DoTime)THEN BEGIN
p
 .Link := r;
.Link := r;EventQueue := p
END
ELSE BEGIN
q := r
 .Link;
.Link;WHILE (q <> NIL) DO
IF (p
 .DoTime <> q
.DoTime <> q  .DoTime)
.DoTime)THEN BEGIN
r := q;
q := q
 .Link
.LinkEND
ELSE q := NIL;
p
 .Link := r
.Link := r  .Link;
.Link;r
 .Link := p
.Link := pEND;
EQL := EQL + 1
END {Schedule};{ }PROCEDURE Preface;
VAR p : Person;
PT : REAL;
PROCEDURE Setup;
BEGIN
EventQueue := NIL;
ClerKQueue.Front := NIL;
ClerkQueue.Rear := NIL;
TaxQueue.Front := NIL;
TaxQueue.Rear := NIL;
EQL := 0; CQL := 0; TQL := 0;
Seed := 1;
Arrivals := 0;
Departures := 0;
ResponseSum := 0;
MeanA := MeanA * 60;
MeanT := MeanT * 60;
Sigma := Sigma * 60;
Mu := Mu * 60;
p := NewPassenger;
PaidTime := TRUNC(0.5 + PT * 60)
END {Setup};{ }BEGIN
Writeln('This is a simulation of an airport customs');Writeln('station, Passengers enter the station with');Writeln('exponentially distributed interarrival times.');Writeln('What mean time (in minutes) would you prefer?');Write('MeanA = '); READLN (MeanA);Writeln('Clerks deal with a new passenger in a normally');Writeln('distributed time. What mean service time would');Writeln('you prefer?');Write('Mu = '); READLN(Mu);Writeln('What standard deviation for this distribution');Writeln('would you prefer?');Write('Sigma = '); READLN(Sigma);Writeln('How many clerks do you prefer at the counter?');Write('IdleClerks = '); READLN(IdleClerks);Writeln('A fraction of the passengers have not paid entry')Writeln('tax and are shuttled to a tax counter. What');Writeln('fraction would you prefer?');Write('NotPaid = '); READLN(NotPaid);Writeln('Tax service requires an exponentially dis-');Writeln('tributed time. What mean time would you prefer?');Write('MeanT = '); READLN(MeanT);Writeln('How many tax men do you prefer at the counter?');Write('IdleTaxMen = '); READLN(IdleTaxMen);Writeln('Passengers re-enter the clerk queue after');Writeln('taxes and are re-serviced in constant time.');Writeln('What time would you prefer?');Write('PaidTime = '); READLN(PT);Writeln('You may run the simulation in segments: and the');Write('state of the system passes on to the next seg');Writeln('ment.');Setup;
Schedule(p)
END {Preface};{ }FUNCTION Empty(VAR Q : WaitingLine) : BOOLEAN;
BEGIN
IF (Q.Front = NIL)
THEN Empty : = TRUE
ELSE Empty : = FALSE
END {Empty};{ }PROCEDURE InsertRear(VAR Q : WaitingLine; VAR p : Person);
BEGIN
p
 .Link := NIL:
.Link := NIL:IF Empty(Q)
THEN Q.Front := p
ELSE Q.Rear
 .LinK := p;
.LinK := p;Q. Rear := p
END {InsertRear};{ }PROCEDURE RemoveFront(VAR Q : WaitingLine; VAR p : Person);
BEGIN
IF Not Empty(Q)
THEN BEGIN
p := Q.Front;
Q.Front := Q.Front
 .Link;
.Link;p
 .DoTime := Clock
.DoTime := ClockEND
END {RemoveFront};{ }PROCEDURE RunAgain(VAR HowLong : INTEGER);
BEGIN
Writeln('The current time is ',Clock);Writeln('How long do you want this run to be?');Write('HowLong = '); READLN(HowLong);HowLong := HowLong * 60
END {RunAgain};{ }FUNCTION NextEvent (VAR EventQueue : Person) : Person;
VAR NoRoom : BOOLEAN;
p : Person ;
s : INTEGER;
BEGIN
NoRoom: = TRUE;
WHILE NoRoom DO BEGIN
NoRoom := FALSE;
p : = EventQueue;
EventQueue : = EventQueue
 .Link;
.Link;EQL : = EQL - 1;
s : p
 .WhatStage;
.WhatStage;IF ((s=2) OR (s=6)) AND (IdleClerks <> 0)
THEN BEGIN
InsertRear(ClerkQueue,p);
CQL : = CQL + 1;
NoRoom : = TRUE
END;
IF ((s=4) AND (IdleTaxMen < = 0))
THEN BEGIN
InsertRear (TaxQueue,p);
TQL := TQL + 1;
NoRoom := TRUE
END
END;
NextEvent : p;
END {NextEvent};{ }PROCEDURE Arrival(VAR p : Person);
VAR q : Person;
BEGIN
Arrivals : = Arrivals + 1;
Clock : =p
 .DoTime;
.DoTime;p
 .Stage [1] : = Clock;
.Stage [1] : = Clock;q := NewPassenger;
Schedule(q);
p
 .WhatStage:= 2;
.WhatStage:= 2;IF (IdleClerks > 0)
THEN Schedule(p)
ELSE BEGIN
InsertRear (ClerkQueue,p);
CQL := CQL + 1
END
END {Arrival}{ }PROCEDURE Depart(p : Person);
VAR s : INTEGER;
BEGIN
Departures := Departures + 1;
s : = p
 .WhatStage ;
.WhatStage ;ResponseSum := ResponseSum + p
 .Stage[s] - p
.Stage[s] - p  .Stage [i];
.Stage [i];DISPOSE(p)
END {Depart};{ }PROCEDURE CheckIn(VAR p : Person);
VAR s,DeltaC : INTEGER;
BEGIN
IdleClerks : = IdleClerks - 1;
Clock := p
 .DoTime;
.DoTime;s := p
 .WhatStage ;
.WhatStage ;p
 .Stage [s] := Clock;
.Stage [s] := Clock;IF (s = 6)
THEN DeltaC := PaidTime
ELSE DeltaC := Normal;
p
 .DoTime := Clock + DeltaC;
.DoTime := Clock + DeltaC;p
 .WhatStage := s + 1;
.WhatStage := s + 1;Schedule(p)
END {CheckIn};{ }PROCEDURE CheckOut(VAR p : Person);
VAR s : INTEGER;
TaxPaid : BOOLEAN;
BEGIN
IdleClerks := IdleClerks + 1;
Clock := p
 .DoTime;
.DoTime;s := p
 .WhatStage;
.WhatStage; .Stage[s] := Clock;
.Stage[s] := Clock;WRITE('CKO ');REPORT(p); {MODEL TRACE}TaxPaid := (s = 7) OR (Random(Seed) > NotPaid);
IF TaxPaid
THEN Depart(p)
ELSE BEGIN
p
 .WhatStage := 4;
.WhatStage := 4;IF IdleTaxMen > 0
THEN Schedule(p)
ELSE BEGIN
InsertRear(TaxQueue,p);
TQL := TQL + 1
END
END;
IF NOT Empty(ClerkQueue)
THEN BEGIN
RemoveFront (ClerkQueue ,p);
Schedule(p);
CQL := CQL - 1
END
END {CheckOut};{ }PROCEDURE TaxIn(VAR p : Person);
VAR s : INTEGER;
BEGIN
IdleTaxMen := IdleTaxMen - 1;
Clock : = p
 .DoTime;
.DoTime;s := p
 .WhatStage;
.WhatStage;p
 .Stage[s] := Clock;
.Stage[s] := Clock;p
 .DoTime := Clock + Expon (MeanT);
.DoTime := Clock + Expon (MeanT);p
 .WhatStage : = s + 1;
.WhatStage : = s + 1;Schedule(p)
END {TaxIn};{ }PROCEDURE TaxOut(VAR p : Person);
VAR s : INTEGER;
BEGIN
IdleTaxMen := IdleTaxMen + 1;
Clock := p
 .DoTime;
.DoTime;s := p
 .WhatStage;
.WhatStage;p
 .Stage[s] := Clock;
.Stage[s] := Clock;p
 .WhatStage := 6;
.WhatStage := 6;IF (IdleClerks > 0)
THEN Schedule(p)
ELSE BEGIN
InsertRear(ClerkQueue,p);
CQL := CQL + 1
END;
IF NOT Empty(TaxQueue)
THEN BEGIN
RemoveFront(TaxQueue,p);
Schedule(p);
TQL := TQL - 1
END
END {TaxOut};{ }PROCEDURE Summary;
VAR ResponseTime : REAL;
BEGIN
Write('There were ' ,Arrivals,' arrivals, and ');Writeln(Departures,' departures.');
ResponseTime := ResponseSum/Departures;
Writeln('The mean amount of time spent in the system');Write('by departing passengers was:', ResponseTime/60);Writeln(' minutes.');Writeln('Number of idle clerks: ', IdleClerks);Writeln('Clerk queue length: ',CQL);Writeln('Number of idle tax men: ',IdleTaxMen);Writeln('Tax queue length: ',TQL);Writeln('Event queue length: ',EQL)END {Summary};{ }BEGIN {AIRPORT}Clock := 0;
Preface;
RunAgain(HowLong);
WHILE (HowLong > 0) DO BEGIN
OverTime := Clock + HowLong;
WHILE (Clock < OverTime) DO BEGIN
p := NextEvent(EventQueue);
CASE p
 .WhatStage OF
.WhatStage OF1 : Arrival(p);
2,6 : CheckIn(p);
3,7 : CheckOut(p);
4 : TaxIn(p);
5 : TaxOut(p)
END
END;
RunAgain(HowLong)
END;
Summary
END {Airport}.


