


Messages are frequently decoded one character at a time or one bit (binary digit) at a time. A variety of coding and decoding structures is available for this task, including a search tree (or a search trie, described in section 8.5.3). The decoding can be done efficiently if the encoding is done so that the most frequently used messages have the shortest paths in the decoding tree. Since files are messages, application of this approach provides file compression.
One extremely short file is:
ABBREVIATE_THIS_SHORT_MESSAGE_AS_MUCH_AS_POSSIBLE_
When sorted and counted, the character frequency of it is:
A 5 F 0 K 0 P 1 U 1 Z 0
B 3 G 1 L 1 Q 0 V 1 _ 8
C 1 H 3 M 2 R 2 W 0
D 0 I 3 N 0 S 8 X 0
E 5 J 0 O 2 T 3 Y 0
The relative frequencies of the letters that actually occur are:
0.16 S _
0.10 A E
0.06 B H I T
0.04 M O R
0.02 C G L P U V
0.00 D F J K N Q W X Y Z
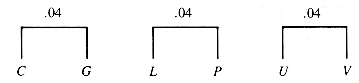
The letters with zero frequency may be ignored, and the symbol SP used for the underscore_. The characters in the file can then be used to form a tree in stages. The characters are first considered to be one-node trees with a value that is their frequency of occurrence. At each stage, the lowest available pair of frequencies is taken as the children of a new node. The new node has an effective frequency that is the sum of the frequencies of its children, since it represents their combination. The process is iterated on the roots of the forest of trees that results from the previous stage. The results of the first three stages of this process are shown in Figure Q.1 and the next three in Figure Q.2. Figure Q.3 illustrates the next two combinations.

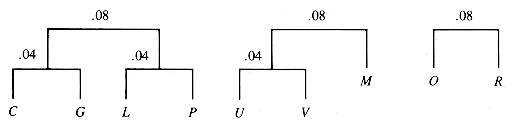
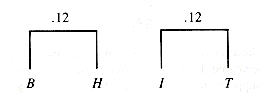
The next two stages join trees of value (0.08 and 0.08) and (0.08 and 0.10). The final result is shown in Figure Q.4.
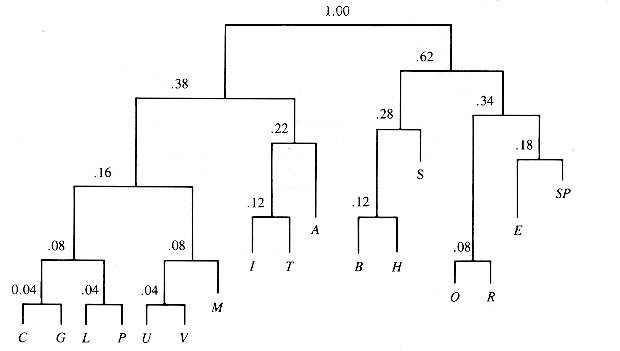
Now assign 0 to left links and 1 to right links and let the sequence of links used to reach a leaf directly from the root be its binary code.
The resulting codes are:
A 011 M 0011 C 00000
S 101 I 0100 G 00001
T 0101 L 00010
B 1000 P 00011
O 1100 U 00100
R 1101 V 00101
H 1001
E 1110
SP 1111
These codes are unique, since the path to any leaf is unique. They also can be separated from each other during decoding, even though they vary in length. Suppose, for example, the following message, encoded by HT, is received:
1010101110011011001
It can be uniquely decoded by simply following the tree links from root to leaves:
The first digit, 1 , means: take the right link.
The second digit, 0, means: take the left link.
The third digit, 1, means: take the right link. This, however, reaches a leaf node, "S". Hence this character code is complete and the next digit begins a new search from the root.
Exercises EQ.1 and EQ.2 are appropriate at this point.
Even for so short a file, there is some compression. If characters are encoded in a standard 8-bit code, this file is 50 X 8 = 400 bits long. Encoded with the tree above, it is 5 X 3 + 3 X 4 + 

 + 8 X 4 = 193 bits in length. In statistical terms, the length of a file encoded with this tree tends to be the expected code length times the number of characters in the file. The expected code length of this tree is
+ 8 X 4 = 193 bits in length. In statistical terms, the length of a file encoded with this tree tends to be the expected code length times the number of characters in the file. The expected code length of this tree is  bits.
bits.
The general algorithm that joins subtrees of highest priority (frequency, probability, and so on) to form a final tree is called the Huffman Algorithm. It remains to describe it in detail.
The entire coding and decoding system must include a way to encode as well as decode. A reasonable structural system is an array Symbol[1 .. N] of symbol nodes, arranged for easy access for encoding--sorted by field Key perhaps. Each node needs to contain the encoding string, Code, of binary digits, to be derived from the Huffman tree after it is constructed.
Each node has a left and right link, which are indices of other nodes in the tree to be constructed. Since the tree contains internal nodes, Symbol actually contains Max = N + (N - 1) nodes. Each node has a field Measure that contains a positive fraction, with the property that the sum of these values from 1 to N is 1.00. The nodes thus have the form:
SymbolType = RECORD
Measure : REAL
Right : INTEGER
Left : INTEGER
Key : {some ordered type
Code : {digit string
END
The heap initially occupies an integer array Map[1 . . N], the values of its cells being pointers to (indices of) nodes in Symbol. (With little change in what follows, the cells of Map could contain pointers into a collection of independent records.) The nodes of Symbol can be heaped indirectly by using Measure values for comparisons, but shifting pointers within Map. For example, UpHeap (section 8.6) becomes:
procedure UpHeap(k)
while k2 do
pINT(k/2)
mkSymbol[Map[k]].Measure
mpSymbol[Map[p]].Measure
if mk < mp
then TempDexMap[k]
Map[k]Map[p]
Map[p]TempDex
kp
else exit
endif
endwhile
end {UpHeapNote that the inequality is reversed, because small measures have high priority.
The required alteration to DownHeap (section 8.6) is similar. The next level of heap management is unaffected:
procedure MakeHeap
for k = 2 to N do
UpHeap(k)
next k
end {MakeHeapThe task of tree-building is accomplished by using the top two items of the heap with an initial directory Map[1 .. N] and adding one combined item derived from them by summing their Measure fields. Eventually there are 2N - 1 items in the heap; the original N values and their combinations pointed to by Map[1 .. 2N - 1].
A modification of DeHeap (section 8.6) is needed. It assumes the symbols are sorted so that the measure of Map[k] is no larger than that of Map[k + 1]:
procedure MakePair(SN) {O(ln SN)
TopLeftMap[1]
LmSymbol[TopLeft].Measure
m2Symbol[Map[2]].Measure
m3Symbol[Map[3]].Measure
if m2 < m3
then Rmm2
TopRightMap[2]
else Rmm3
TopRightMap[3]
endif
SNSN + 1
Symbol[SN].LeftTopLeft
Symbol[SN].RightTopRight
Symbol[SN].MeasureLm + Rm
UpHeap(SN)
end {MakePairOnce the arrays and Symbol have been initialized for N nodes, the tree is constructed and located by:
function Huff Tree {O(N  ln N)
ln N)
SNN
for k = 1 to N - 1 do MakePair(SN) next k
return Map[1]
end {Huff TreeFinally, the codes are determined for encoding by a traverse of the tree:
If d1d2 . . . dk is the code string for a parent, then d1d2 . . . dk 0 is the code for the left child, and d1 d2 . . . dk 1 is the code for the right child. Every node is reached from its parent.
The position of a given symbol can be tracked by initializing Track[k] to k and incorporating two statements into the then condition of UpHeap just before the switch of Map values:
Track[Map[k]]p
Track[Map[p]]k
The final value of Track[k] is the index m such that Map[m] = k--the heap position of Symbol[k].
Exercises immediate application of text materials
EQ.1 Decode the rest of the message used as an example in this section.
EQ.2 Form a Huffman tree from the file:
THIS_STUFF_IS_OLD_HAT
Problem not immediate, but requiring no major extensions of the text
PQ.1 Put together the entire Huffman code construction for a set of N frequency counts.
Program for trying it yourself
PGQ.1 Write a program that reads a sequence of characters and displays the corresponding Huffman tree.
Project for fun; for serious students
PJQ.1 Write a program that uses one text file to generate a Huffman tree, then will accept other files and encode a text file or decode a binary string that has been encoded with the same tree.
Problem
Program
Project