3.1 INTRODUCTION
Three of the most commonly used file structures for information retrieval can be classified as lexicographical indices (indices that are sorted), clustered file structures, and indices based on hashing. One type of lexicographical index, the inverted file, is presented in this chapter, with a second type of lexicographical index, the Patricia (PAT) tree, discussed in Chapter 5. Clustered file structures are covered in Chapter 16, and indices based on hashing are covered in Chapter 13 and Chapter 4 (signature files).
The concept of the inverted file type of index is as follows. Assume a set of documents. Each document is assigned a list of keywords or attributes, with optional relevance weights associated with each keyword (attribute). An inverted file is then the sorted list (or index) of keywords (attributes), with each keyword having links to the documents containing that keyword (see Figure 3.1) . This is the kind of index found in most commercial library systems. The use of an inverted file improves search efficiency by several orders of magnitude, a necessity for very large text files. The penalty paid for this efficiency is the need to store a data structure that ranges from 10 percent to 100 percent or more of the size of the text itself, and a need to update that index as the data set changes.
Usually there are some restrictions imposed on these indices and consequently on later searches. Examples of these restrictions are:
It should be noted that the restrictions that determine what is to be indexed are critical to later search effectiveness and therefore these rules should be carefully constructed and evaluated. This problem is further discussed in Chapter 7.
A search in an inverted file is the composition of two searching algorithms; a search for a keyword (attribute), which returns an index, and then a possible search on that index for a particular attribute value. The result of a search on an inverted file is a set of records (or pointers to records).
This Chapter is organized as follows. The next section presents a survey of the various implementation structures for inverted files. The third section covers the complete implementation of an algorithm for building an inverted file that is stored as a sorted array, and the fourth section shows two variations on this implementation, one that uses no sorting (and hence needs little working storage) and one that increases efficiency by making extensive use of primary memory. The final section summarizes the chapter.
There are several structures that can be used in implementing inverted files: sorted arrays, B-trees, tries, and various hashing structures, or combinations of these structures. The first three of these structures are sorted (lexicographically) indices, and can efficiently support range queries, such as all documents having keywords that start with "comput." Only these three structures will be further discussed in this chapter. (For more on hashing methods, see Chapters 4 and 13.)
An inverted file implemented as a sorted array structure stores the list of keywords in a sorted array, including the number of documents associated with each keyword and a link to the documents containing that keyword. This array is commonly searched using a standard binary search, although large secondary-storage-based systems will often adapt the array (and its search) to the characteristics of their secondary storage.
The main disadvantage of this approach is that updating the index (for example appending a new keyword) is expensive. On the other hand, sorted arrays are easy to implement and are reasonably fast. (For this reason, the details of creating a sorted array inverted file are given in section 3.3.)
Another implementation structure for an inverted file is a B-tree. More details of B-trees can be found in Chapter 2, and also in a recent paper (Cutting and Pedersen 1990) on efficient inverted files for dynamic data (data that is heavily updated). A special case of the B-tree, the prefix B-tree, uses prefixes of words as primary keys in a B-tree index (Bayer and Unterauer 1977) and is particularly suitable for storage of textual indices. Each internal node has a variable number of keys. Each key is the shortest word (in length) that distinguishes the keys stored in the next level. The key does not need to be a prefix of an actual term in the index. The last level or leaf level stores the keywords themselves, along with their associated data (see Figure 3.2). Because the internal node keys and their lengths depend on the set of keywords, the order (size) of each node of the prefix B-tree is variable. Updates are done similarly to those for a B-tree to maintain a balanced tree. The prefix B-tree method breaks down if there are many words with the same (long) prefix. In this case, common prefixes should be further divided to avoid wasting space.
Compared with sorted arrays, B-trees use more space. However, updates are much easier and the search time is generally faster, especially if secondary storage is used for the inverted file (instead of memory). The implementation of inverted files using B-trees is more complex than using sorted arrays, and therefore readers are referred to Knuth (1973) and Cutting and Pedersen (1990) for details of implementation of B-trees, and to Bayer and Unterauer (1977) for details of implementation of prefix B-trees.
Inverted files can also be implemented using a trie structure (see Chapter 2 for more on tries). This structure uses the digital decomposition of the set of keywords to represent those keywords. A special trie structure, the Patricia (PAT) tree, is especially useful in information retrieval and is described in detail in Chapter 5. An additional source for tested and optimized code for B-trees and tries is Gonnet and Baeza-Yates (1991).
The production of sorted array inverted files can be divided into two or three sequential steps as shown in Figure 3.3. First, the input text must be parsed into a list of words along with their location in the text. This is usually the most time consuming and storage consuming operation in indexing. Second, this list must then be inverted, from a list of terms in location order to a list of terms ordered for use in searching (sorted into alphabetical order, with a list of all locations attached to each term). An optional third step is the postprocessing of these inverted files, such as for adding term weights, or for reorganizing or compressing the files.
Creating the initial word list requires several different operations. First, the individual words must be recognized from the text. Each word is then checked against a stoplist of common words, and if it can be considered a noncommon word, may be passed through a stemming algorithm. The resultant stem is then recorded in the word-within-location list. The parsing operation and the use of a stoplist are described in Chapter 7, and the stemming operation is described in Chapter 8.
The word list resulting from the parsing operation (typically stored as a disk file) is then inverted. This is usually done by sorting on the word (or stem), with duplicates retained (see Figure 3.4). Even with the use of high-speed sorting utilities, however, this sort can be time consuming for large data sets (on the order of n log n). One way to handle this problem is to break the data sets into smaller pieces, process each piece, and then correctly merge the results. Methods that do not use sorting are given in section 3.4.1. After sorting, the duplicates are merged to produce within-document frequency statistics. (A system not using within-document frequencies can just sort with duplicates removed.) Note that although only record numbers are shown as locations in Figure 3.4, typically inverted files store field locations and possibly even word location. These additional locations are needed for field and proximity searching in Boolean operations and cause higher inverted file storage overhead than if only record location was needed. Inverted files for ranking retrieval systems (see Chapter 14) usually store only record locations and term weights or frequencies.
Although an inverted file could be used directly by the search routine, it is usually processed into an improved final format. This format is based on the search methods and the (optional) weighting methods used. A common search technique is to use a binary search routine on the file to locate the query words. This implies that the file to be searched should be as short as possible, and for this reason the single file shown containing the terms, locations, and (possibly) frequencies is usually split into two pieces. The first piece is the dictionary containing the term, statistics about that term such as number of postings, and a pointer to the location of the postings file for that term. The second piece is the postings file itself, which contains the record numbers (plus other necessary location information) and the (optional) weights for all occurrences of the term. In this manner, the dictionary used in the binary search has only one "line" per unique term. Figure 3.5 illustrates the conceptual form of the necessary files; the actual form depends on the details of the search routine and on the hardware being used. Work using large data sets (Harman and Candela 1990) showed that for a file of 2,653 records, there were 5,123 unique terms with an average of 14 postings/term and a maximum of over 2,000 postings for a term. A larger data set of 38,304 records had dictionaries on the order of 250,000 lines (250,000 unique terms, including some numbers) and an average of 88 postings per record. From these numbers it is clear that efficient storage structures for both the binary search and the reading of the postings are critical.
Two different techniques are presented as improvements on the basic inverted file creation discussed in section 3.3. The first technique is for working with very large data sets using secondary storage. The second technique uses multiple memory loads for inverting files.
Indexing large data sets using the basic inverted file method presents several problems. Most computers cannot sort the very large disk files needed to hold the initial word list within a reasonable time frame, and do not have the amount of storage necessary to hold a sorted and unsorted version of that word list, plus the intermediate files involved in the internal sort. Whereas the data set could be broken into smaller pieces for processing, and the resulting files properly merged, the following technique may be considerably faster. For small data sets, this technique carries a significant overhead and therefore should not be used. (For another approach to sorting large amounts of data, see Chapter 5.)
The new indexing method (Harman and Candela 1990) is a two-step process that does not need the middle sorting step. The first step produces the initial inverted file, and the second step adds the term weights to that file and reorganizes the file for maximum efficiency (see Figure 3.6).
The creation of the initial inverted file avoids the use of an explicit sort by using a right-threaded binary tree (Knuth 1973). The data contained in each binary tree node is the current number of term postings and the storage location of the postings list for that term. As each term is identified by the text parsing program, it is looked up in the binary tree, and either is added to the tree, along with related data, or causes tree data to be updated. The postings are stored as multiple linked lists, one variable length linked list for each term, with the lists stored in one large file. Each element in the linked postings file consists of a record number (the location of a given term), the term frequency in that record, and a pointer to the next element in the linked list for that given term. By storing the postings in a single file, no storage is wasted, and the files are easily accessed by following the links. As the location of both the head and tail of each linked list is stored in the binary tree, the entire list does not need to be read for each addition, but only once for use in creating the final postings file (step two).
Note that both the binary tree and the linked postings list are capable of further growth. This is important in indexing large data sets where data is usually processed from multiple separate files over a short period of time. The use of the binary tree and linked postings list could be considered as an updatable inverted file. Although these structures are not as efficient to search, this method could be used for creating and storing supplemental indices for use between updates to the primary index. However, see the earlier discussion of B-trees for better ways of producing updatable inverted files.
The binary tree and linked postings lists are saved for use by the term weighting routine (step two). This routine walks the binary tree and the linked postings list to create an alphabetical term list (dictionary) and a sequentially stored postings file. To do this, each term is consecutively read from the binary tree (this automatically puts the list in alphabetical order), along with its related data. A new sequentially stored postings file is allocated, with two elements per posting. The linked postings list is then traversed, with the frequencies being used to calculate the term weights (if desired). The last step writes the record numbers and corresponding term weights to the newly created sequential postings file. These sequentially stored postings files could not be created in step one because the number of postings is unknown at that point in processing, and input order is text order, not inverted file order. The final index files therefore consist of the same dictionary and sequential postings file as for the basic inverted file described in section 3.3.
Table 3.1 gives some statistics showing the differences between an older indexing scheme and the new indexing schemes. The old indexing scheme refers to the indexing method discussed in section 3.3 in which records are parsed into a list of words within record locations, the list is inverted by sorting, and finally the term weights are added.
Note that the size of the final index is small, only 8 percent of the input text size for the 50 megabyte database, and around 14 percent of the input text size for the larger databases. The small size of the final index is caused by storing only the record identification number as location. As this index was built for a ranking retrieval system (see Chapter 14), each posting contains both a record id number and the term's weight in that record. This size remains constant when using the new indexing method as the format of the final indexing files is unchanged. The working storage (the storage needed to build the index) for the new indexing method is not much larger than the size of the final index itself, and substantially smaller than the size of the input text. However, the amount of working storage needed by the older indexing method would have been approximately 933 megabytes for the 359 megabyte database, and over 2 gigabytes for the 806 megabyte database, an amount of storage beyond the capacity of many environments. The new method takes more time for the very small (1.6 megabyte) database because of its additional processing overhead. As the size of the database increases, however, the processing time has an n log n relationship to the size of the database. The older method contains a sort (not optimal) which is n log n (best case) to n squared (worst case), making processing of the very large databases likely to have taken longer using this method.
The second technique to produce a sorted array inverted file is a fast inversion algorithm called FAST-INV (Copyright © Edward A. Fox, Whay C. Lee, Virginia Tech). This technique takes advantage of two principles: the large primary memories available on today's computers and the inherent order of the input data. The following summary of this technique is adapted from a technical report by Fox and Lee (1991).
The first principle is important since personal computers with more than 1 megabyte of primary memory are common, and mainframes may have more than 100 megabytes of memory. Even if databases are on the order of 1 gigabyte, if they can be split into memory loads that can be rapidly processed and then combined, the overall cost will be minimized.
The second principle is crucial since with large files it is very expensive to use polynomial or even n log n sorting algorithms. These costs are further compounded if memory is not used, since then the cost is for disk operations.
The FAST-INV algorithm follows these two principles, using primary memory in a close to optimal fashion, and processing the data in three passes. The overall scheme can be seen in Figure 3.7.
The input to FAST-INV is a document vector file containing the concept vectors for each document in the collection to be indexed. A sample document vector file can be seen in Figure 3.8. The document numbers appear in the left-hand column and the concept numbers of the words in each document appear in the right- hand column. This is similar to the initial word list shown in Figure 3.4 for the basic method, except that the words are represented by concept numbers, one concept number for each unique word in the collection (i.e., 250,000 unique words implies 250,000 unique concept numbers). Note however that the document vector file is in sorted order, so that concept numbers are sorted within document numbers, and document numbers are sorted within collection. This is necessary for FAST-INV to work correctly.
Preparation
In order to better explain the FAST-INV algorithm, some definitions are needed.
In the first pass, the entire document vector file can be read and two new files produced: a file of concept postings/pointers (CONPTR) and a load table. It is assumed that M >> HCN, so these two files can be built in primary memory. However, it is assumed that M < L, so several primary memory loads will be needed to process the document data. Because entries in the document vector file will already be grouped by concept number, with those concepts in ascending order, it is appropriate to see if this data can be somehow transformed beforehand into j parts such that:
L / j < M, so that each part will fit into primary memory
HCN / j concepts, approximately, are associated with each part
This allows each of the j parts to be read into primary memory, inverted there, and the output to be simply appended to the (partially built) final inverted file.
Specifically, preparation involves the following:
1. Allocate an array, con_entries_cnt, of size HCN, initialized to zero.
2. For each <doc#,con#> entry in the document vector file: increment con_entries_cnt[con#] .
3. Use the just constructed con_entries_cnt to create a disk version of CONPTR.
4. Initialize the load table.
5. For each <con#,count> pair obtained from con_entries_cnt: if there is no room for documents with this concept to fit in the current load, then create an entry in the load table and initialize the next load entry; otherwise update information for the current load table entry.
After one pass through the input, the CONPTR file has been built and the load table needed in later steps of the algorithm has been constructed. Note that the test for room in a given load enforces the constraint that data for a load will fit into available memory. Specifically:
Then the constraint that must be met for another concept to be added to the current load is
8 * LL + 4 * S < M
Splitting document vector file
The load table indicates the range of concepts that should be processed for each primary memory load. There are two approaches to handling the multiplicity of loads. One approach, which is currently used, is to make a pass through the document vector file to obtain the input for each load. This has the advantage of not requiring additional storage space (though that can be obviated through the use of magnetic tapes), but has the disadvantage of requiring expensive disk I/O.
The second approach is to build a new copy of the document vector collection, with the desired separation into loads. This can easily be done using the load table, since sizes of each load are known, in one pass through the input. As each document vector is read, it is separated into parts for each range of concepts in the load table, and those parts are appended to the end of the corresponding section of the output document collection file. With I/O buffering, the expense of this operation is proportional to the size of the files, and essentially costs the same as copying the file.
Inverting each load
When a load is to be processed, the appropriate section of the CONPTR file is needed. An output array of size equal to the input document vector file subset is needed. As each document vector is processed, the offset (previously recorded in CONPTR) for a given concept is used to place the corresponding document/weight entry, and then that offset is incremented. Thus, the CONPTR data allows the input to be directly mapped to the output, without any sorting. At the end of the input load the newly constructed output is appended to the inverted file.
An example
Figure 3.9 illustrates the FAST-INV processing using sample data. The document vector input files are read through once to produce the concept postings/pointers file (stored on disk as CONPTR) and the load table. Three loads will be needed, for concepts in ranges 1-4, 5-11, and 12-14. There are 10 distinct concepts, and HCN is 14.
The second phase of processing uses the load table to split the input document vector files and create the document vector loads files. There are three parts, corresponding to the three loads. It can be seen that the document vectors in each load are shortened since only those concepts in the allowable range for the load are included.
The final phase of processing involves inverting each part of the document vectors loads file, using primary memory, and appending the result to the inverted file. The appropriate section of the CONPTR file is used so that inversion is simply a copying of data to the correct place, rather than a sort.
Performance results
Based on the discussion above, it can be seen that FAST-INV is a linear algorithm in the size of the input file, L. The input disk files must be read three times, and written twice (using the second splitting scheme). Processing in primary memory is limited to scans through the input, with appropriate (inexpensive) computation required on each entry.
Thus, it should be obvious that FAST-INV should perform well in comparison to other inversion methods, such as those used in other systems such as SIRE and SMART. To demonstrate this fact, a variety of tests were made. Table 3.2 summarizes the results for indexing the 12,684 document/8.68 megabyte INSPEC collection.
More details of these results, including the various loading experiments made during testing, can be found in the full technical report (Fox and Lee 1991).
This Chapter has presented a survey of inverted file structures and detailed the actual building of a basic sorted array type of inverted file. Two modifications that are effective for indexing large data collections were also presented.
BAYER, R., and K. UNTERAUER. 1977. "Prefix B-Trees." ACM Transactions on Database Systems, 2(1), 11-26.
CUTTING, D., and J. PEDERSEN. 1990. "Optimizations for Dynamic Inverted Index Maintenance." Paper presented at the 13th International Conference on Research and Development in Information Retrieval. Brussels, Belgium.
FOX, E. A., and W. C. LEE. 1991. "FAST-INV: A Fast Algorithm for Building Large Inverted Files." Technical Report TR-91-10, VPI&SU Department of Computer Science, March, 1991. Blacksburg, Va. 24061-0106.
GONNET, G. H., and R. BAEZA-YATES. 1991. Handbook of Algorithms and Data Structures (2nd ed.). Reading, Mass.: Addison-Wesley.
HARMAN, D., and G. CANDELA. 1990. "Retrieving Records from a Gigabyte of Text on a Minicomputer using Statistical Ranking." Journal of the American Society for Information Science, 41(8), 581-89.
KNUTH, DONALD E. 1973. The Art of Computer Programming. Reading, Mass.: Addison-Wesley.
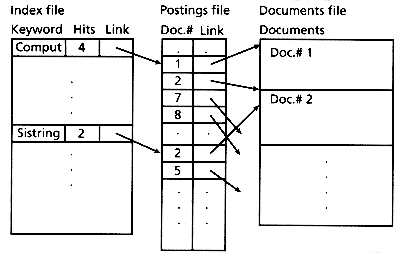
Figure 3.1: An inverted file implemented using a sorted array
 a controlled vocabulary which is the collection of keywords that will be indexed. Words in the text that are not in the vocabulary will not be indexed, and hence are not searchable.
a controlled vocabulary which is the collection of keywords that will be indexed. Words in the text that are not in the vocabulary will not be indexed, and hence are not searchable. a list of stopwords (articles, prepositions, etc.) that for reasons of volume or precision and recall will not be included in the index, and hence are not searchable.
a list of stopwords (articles, prepositions, etc.) that for reasons of volume or precision and recall will not be included in the index, and hence are not searchable. a set of rules that decide the beginning of a word or a piece of text that is indexable. These rules deal with the treatment of spaces, punctuation marks, or some standard prefixes, and may have signficant impact on what terms are indexed.
a set of rules that decide the beginning of a word or a piece of text that is indexable. These rules deal with the treatment of spaces, punctuation marks, or some standard prefixes, and may have signficant impact on what terms are indexed. a list of character sequences to be indexed (or not indexed). In large text databases, not all character sequences are indexed; for example, character sequences consisting of all numerics are often not indexed.
a list of character sequences to be indexed (or not indexed). In large text databases, not all character sequences are indexed; for example, character sequences consisting of all numerics are often not indexed.3.2 STRUCTURES USED IN INVERTED FILES
3.2.1 The Sorted Array
3.2.2 B-trees
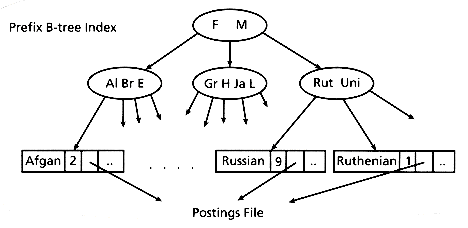
Figure 3.2: A prefix B-tree
3.2.3 Tries
3.3 BUILDING AN INVERTED FILE USING A SORTED ARRAY
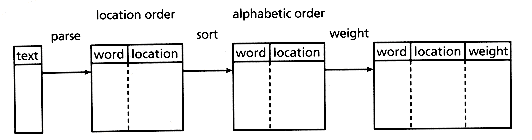
Figure 3.3: Overall schematic of sorted array inverted file creation
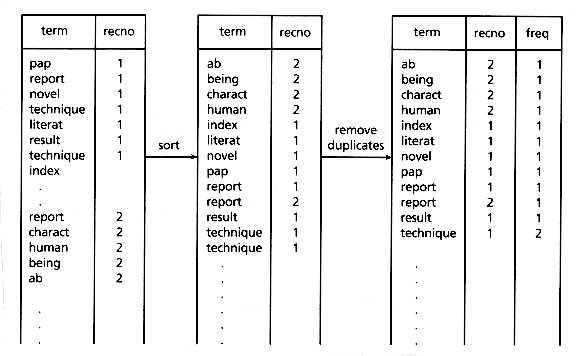
Figure 3.4: Inversion of word list
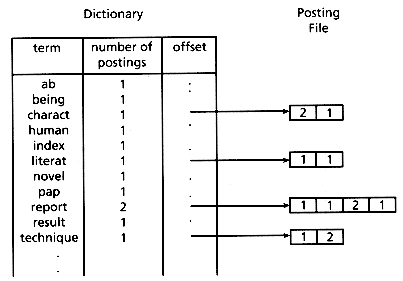
Figure 3.5: Dictionary and postings file from the last example
3.4 MODIFICATIONS TO THE BASIC TECHNIQUE
3.4.1 Producing an Inverted File for Large Data Sets without Sorting
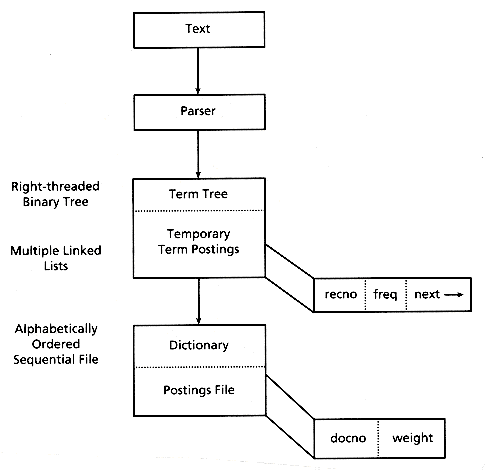
Figure 3.6: Flowchart of new indexing method
Table 3.1: Indexing Statistics
Text Size Indexing Time Working Storage Index Storage
(megabytes) (hours) (megabytes) (megabytes)
----------------------------------------------------------
old new old new old new
1.6 0.25 0.50 4.0 0.70 0.4 0.4
50 8 10.5 132 6 4 4
359 -- 137 -- 70 52 52
806 -- 313 -- 163 112 112
3.4.2 A Fast Inversion Algorithm
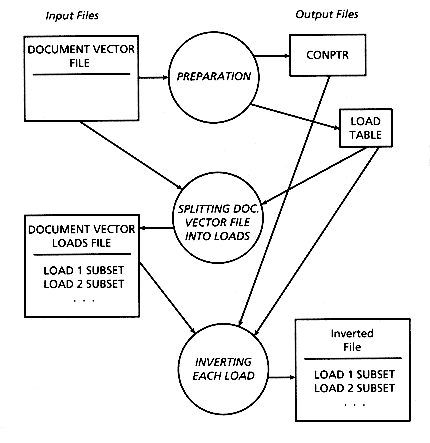
Figure 3.7: Overall scheme of FAST-INV
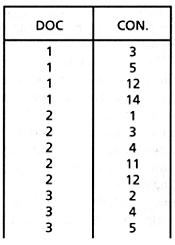
Figure 3.8: Sample document vector
HCN = highest concept number in dictionary
L = number of document/concept (or concept/document) pairs in the collection
M = available primary memory size, in bytes
Let LL = length of current load (i.e., number of concept/weight pairs)
S = spread of concept numbers in the current load (i.e., end concept - start concept + 1 )
8 bytes = space needed for each concept/weight pair
4 bytes = space needed for each concept to store count of postings for it
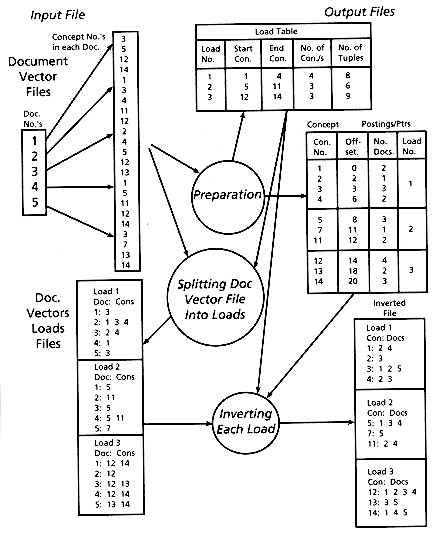
Figure 3.9: A FAST-INV example
Table 3.2: Real Time Requirements (min.)[:sec.] for SIRE, SMART
Method Comments Indexing Inversion
--------------------------------------------------------------
SIRE Dictionary built during inversion 35 72
SMART Dictionary built during indexing 49 11
FAST-INV Dictionary built during indexing 49 1:14
3.5 SUMMARY
REFERENCES


