7.1 INTRODUCTION
Lexical analysis is the process of converting an input stream of characters into a stream of words or tokens. Tokens are groups of characters with collective significance. Lexical analysis is the first stage of automatic indexing, and of query processing. Automatic indexing is the process of algorithmically examining information items to generate lists of index terms. The lexical analysis phase produces candidate index terms that may be further processed, and eventually added to indexes (see Chapter 1 for an outline of this process). Query processing is the activity of analyzing a query and comparing it to indexes to find relevant items. Lexical analysis of a query produces tokens that are parsed and turned into an internal representation suitable for comparison with indexes.
In automatic indexing, candidate index terms are often checked to see whether they are in a stoplist, or negative dictionary. Stoplist words are known to make poor index terms, and they are immediately removed from further consideration as index terms when they are identified.
This chapter discusses the design and implementation of lexical analyzers and stoplists for information retrieval. These topics go well together because, as we will see, one of the most efficient ways to implement stoplists is to incorporate them into a lexical analyzer.
The first decision that must be made in designing a lexical analyzer for an automatic indexing system is: What counts as a word or token in the indexing scheme? At first, this may seem an easy question, and there are some easy answers to it--for example, terms consisting entirely of letters should be tokens. Problems soon arise, however. Consider the following:
There is no technical difficulty in solving any of these problems, but information system designers must think about them carefully when setting lexical analysis policy. Recognizing numbers as tokens adds many terms with poor discrimination value to an index, but may be a good policy if exhaustive searching is important. Breaking up hyphenated terms increases recall but decreases precision, and may be inappropriate in some fields (like an author field). Preserving case distinctions enhances precision but decreases recall.
Commercial information systems differ somewhat in their lexical analysis policies, but are alike in usually taking a conservative (recall enhancing) approach. For example, Chemical Abstracts Service, ORBIT Search Service, and Mead Data Central's LEXIS/NEXIS all recognize numbers and words containing digits as index terms, and all are case insensitive. None has special provisions for most punctuation marks in most indexed fields. However, Chemical Abstracts Service keeps hyphenated words as single tokens, while the ORBIT Search Service and LEXIS/NEXIS break them apart (if they occur in title or abstract fields).
The example we use to illustrate our discussion is simple so it can be explained easily, and because the simplest solution often turns out to be best. Modifications to it based on the considerations discussed above are easy to make. In the example, any nonempty string of letters and digits, not beginning with a digit, is regarded as a token. All letters are converted to lower case. All punctuation, spacing, and control characters are treated as token delimiters.
Designing a lexical analyzer for query processing is like designing one for automatic indexing. It also depends on the design of the lexical analyzer for automatic indexing: since query search terms must match index terms, the same tokens must be distinguished by the query lexical analyzer as by the indexing lexical analyzer. In addition, however, the query lexical analyzer must usually distinguish operators (like the Boolean operators, stemming or truncating operators, and weighting function operators), and grouping indicators (like parentheses and brackets). A lexical analyzer for queries should also process certain characters, like control characters and disallowed punctuation characters, differently from one for automatic indexing. Such characters are best treated as delimiters in automatic indexing, but in query processing, they indicate an error. Hence, a query lexical analyzer should flag illegal characters as unrecognized tokens.
The example query lexical analyzer presented below recognizes left and right parentheses (as grouping indicators), ampersand, bar, and caret (as Boolean operators), and any alphanumeric string beginning with a letter (as search terms). Spacing characters are treated as delimiters, and other characters are returned as unrecognized tokens. All uppercase characters are converted to lowercase.
Lexical analysis is expensive because it requires examination of every input character, while later stages of automatic indexing and query processing do not. Although no studies of the cost of lexical analysis in information retrieval systems have been done, lexical analysis has been shown to account for as much as 50 percent of the computational expense of compilation (Wait 1986). Thus, it is important for lexical analyzers, particularly for automatic indexing, to be as efficient as possible.
Lexical analysis for information retrieval systems is the same as lexical analysis for other text processing systems; in particular, it is the same as lexical analysis for program translators. This problem has been studied thoroughly, so we ought to adopt the solutions in the program translation literature (Aho, Sethi, and Ullman 1986). There are three ways to implement a lexical analyzer:
The first approach, using a lexical analyzer generator, is best when the lexical analyzer is complicated; if the lexical analyzer is simple, it is usually easier to implement it by hand. In our discussion of stoplists below, we present a special purpose lexical analyzer generator for automatic indexing that produces efficient lexical analyzers that filter stoplist words. Consequently, we defer further discussion of this alternative.
The second alternative is the worst. An ad hoc algorithm, written just for the problem at hand in whatever way the programmer can think to do it, is likely to contain subtle errors. Furthermore, finite state machine algorithms are extremely fast, so ad hoc algorithms are likely to be less efficient.
The third approach is the one we present in this section. We assume some knowledge of finite state machines (also called finite automata), and their use in program translation systems. Readers unfamiliar with these topics can consult Hopcroft and Ullman (1979), and Aho, Sethi, and Ullman (1986). Our example is an implementation of a query lexical analyzer as described above.
The easiest way to begin a finite state machine implementation is to draw a transition diagram for the target machine. A transition diagram for a machine recognizing tokens for our example query lexical analyzer is pictured in Figure 7.1.
In this diagram, characters fall into ten classes: space characters, letters, digits, the left and right parentheses, ampersand, bar, caret, the end of string character, and all other characters. The first step in implementing this finite state machine is to build a mechanism for classifying characters. The easiest and fastest way to do this is to preload an array with the character classes for the character set. Assuming the ASCII character set, such an array would contain 128 elements with the character classes for the corresponding ASCII characters. If such an array is called char_class, for example, then the character class for character 'c' is simply char_class [c]. The character classes themselves form a distinct data type best declared as an enumeration in C. Figure 7.2 contains C declarations for a character class type and array. (Note that the end of file character requires special treatment in C because it is not part of ASCII).
The same technique is used for fast case conversion. In Figure 7.2, an array of 128 characters called convert_case is preloaded with the printing characters, with lowercase characters substituted for uppercase characters. Nonprinting character positions will not be used, and are set to 0.
There also needs to be a type for tokens. An enumeration type is best for this as well. This type will have an element for each of the tokens: term, left parenthesis, right parenthesis, ampersand, bar, caret, end of string, and the unrecognized token. Processing is simplified by matching the values of the enumeration type to the final states of the finite state machine. The declaration of the token type also appears in Figure 7.2.
The code for the finite state machine must keep track of the current state, and have a way of changing from state to state on input. A state change is called a transition. Transition information can be encoded in tables, or in flow of control. When there are many states and transitions, a tabular encoding is preferable; in our example, a flow of control encoding is probably clearest. Our example implementation reads characters from an input stream supplied as a parameter. The routine returns the next token from the input each time it is called. If the token is a term, the text of the term (in lowercase) is written to a term buffer supplied as a parameter. Our example code appears in Figure 7.3.
The algorithm begins in state 0. As each input character is consumed, a switch on the state determines the transition. Input is consumed until a final state (indicated by a negative state number) is reached. When recognizing a term, the algorithm keeps reading until some character other than a letter or a digit is found. Since this character may be part of another token, it must be pushed back on the input stream. The final state is translated to a token type value by changing its sign and coercing it to the correct type (this was the point of matching the token type values to the final machine states).
Figure 7.4 contains a small main program to demonstrate the use of this lexical analyzer. The program reads characters from a file named on the command line, and writes out a description of the token stream that it finds. In real use, the tokens returned by the lexical analyzer would be processed by a query parser, which would also probably call retrieval and display routines.
The code above, augmented with the appropriate include files, is a complete and efficient implementation of our simple lexical analyzer for queries. When tested, this code tokenized at about a third the speed that the computer could read characters--about as fast as can be expected. An even simpler lexical analyzer for automatic indexing can be constructed in the same way, and it will be just as fast.
It has been recognized since the earliest days of information retrieval (Luhn 1957) that many of the most frequently occurring words in English (like "the," "of," "and," "to," etc.) are worthless as index terms. A search using one of these terms is likely to retrieve almost every item in a database regardless of its relevance, so their discrimination value is low (Salton and McGill 1983; van Rijsbergen 1975). Furthermore, these words make up a large fraction of the text of most documents: the ten most frequently occurring words in English typically account for 20 to 30 percent of the tokens in a document (Francis and Kucera 1982). Eliminating such words from consideration early in automatic indexing speeds processing, saves huge amounts of space in indexes, and does not damage retrieval effectiveness. A list of words filtered out during automatic indexing because they make poor index terms is called a stoplist or a negative dictionary.
One way to improve information retrieval system performance, then, is to eliminate stopwords during automatic indexing. As with lexical analysis, however, it is not clear which words should be included in a stoplist. Traditionally, stoplists are supposed to have included the most frequently occurring words. However, some frequently occurring words are too important as index terms. For example, included among the 200 most frequently occurring words in general literature in English are "time," "war," "home," "life," "water," and "world." On the other hand, specialized databases will contain many words useless as index terms that are not frequent in general English. For example, a computer literature database probably need not use index terms like "computer," "program," "source," "machine," and "language."
As with lexical analysis in general, stoplist policy will depend on the database and features of the users and the indexing process. Commercial information systems tend to take a very conservative approach, with few stopwords. For example, the ORBIT Search Service has only eight stopwords: "and," "an," "by," "from," "of," "the," and "with." Larger stoplists are usually advisable. An oft-cited example of a stoplist of 250 words appears in van Rijsbergen (1975). Figure 7.5 contains a stoplist of 425 words derived from the Brown corpus (Francis and Kucera 1982) of 1,014,000 words drawn from a broad range of literature in English. Fox (1990) discusses the derivation of (a slightly shorter version of) this list, which is specially constructed to be used with the lexical analysis generator described below.
There are two ways to filter stoplist words from an input token stream: (a) examine lexical analyzer output and remove any stopwords, or (b) remove stopwords as part of lexical analysis.
The first approach, filtering stopwords from lexical analyzer output, makes the stoplist problem into a standard list searching problem: every token must be looked up in the stoplist, and removed from further analysis if found. The usual solutions to this problem are adequate, including binary search trees, binary search of an array, and hashing (Tremblay and Sorenson, 1984, Chapter 13). Undoubtedly the fastest solution is hashing.
When hashing is used to search a stoplist, the list must first be inserted into a hash table. Each token is then hashed into the table. If the resulting location is empty, the token is not a stopword, and is passed on; otherwise, comparisons must be made to determine whether the hashed value really matches the entries at that hash table location. If not, then the token is passed on; if so, the token is a word, and is eliminated from the token stream. This strategy is fast, but is slowed by the need to re-examine each character in a token to generate its hash value, and by the need to resolve collisions.
The hashing strategy can be improved by incorporating computation of hash values into the character-by-character processing of lexical analysis. The output of the lexical analysis phase is then a hash value as well as a token, with a small increase in the cost of lexical analysis. Some improvement can also be realized by generating a perfect hashing function for the stoplist (a perfect hashing function for a set of keys hashes the keys with no collisions-see Chapter 13). This minimizes the overhead of collision resolution, but has no effect on the number of collisions, which is sure to be large unless the hash table is enormous.
Although hashing is an excellent approach, probably the best implementation of stoplists is the second strategy: remove stoplist words as part of the lexical analysis process. Since lexical analysis must be done anyway, and recognizing even a large stoplist can be done at almost no extra cost during lexical analysis, this approach is extremely efficient. Furthermore, lexical analyzers that filter stoplists can be generated automatically, which is easier and less error-prone than writing stopword filters by hand.
The rest of this chapter presents a lexical analyzer generator for automatic indexing. The lexical analyzer generator accepts an arbitrary list of stopwords. It should be clear from the code presented here how to elaborate the generator, or the driver program, to fit other needs.
The heart of the lexical analyzer generator is its algorithm for producing a finite state machine. The algorithm presented here is based on methods of generating minimum state deterministic finite automata (DFAs) using derivatives of regular expressions (Aho and Ullman 1975) adapted for lists of strings. (A DFA is minimum state if it has a few states as possible.) This algorithm is similar to one described by Aho and Corasick (1975) for string searching.
During machine generation, the algorithm labels each state with the set of strings the machine would accept if that state were the initial state. It is easy to examine these state labels to determine: (a) the transition out of each state, (b) the target state for each transition, and (c) the states that are final states. For example, suppose a state is labeled with the set of strings {a, an, and, in, into, to}. This state must have transitions on a, i, and t. The transition on a must go to a state labeled with the set {n, nd,
An algorithm for generating a minimum state DFA using this labeling mechanism is presented in Figure 7.6. An example of a fully constructed machine appears in Figure 7.7.
A C language implementation for this algorithm for generating a finite state machine appears in Figure 7.8. This algorithm relies on simple routines for allocating memory and manipulating lists of strings not listed to save space.
Several techniques are used to speed up the algorithm and to save space. State labels are hashed to produce a signature for faster label searching. Labels are also kept in a binary search tree by hash signature. To save space in the transition table, which is very sparse, transitions are kept in a short list that is searched whenever a transition for a given state is needed. These lists usually have no more than three or four items, so searching them is still reasonably fast. Once the machine is constructed, all the space used tor the state labels is deallocated, so the only data structures of any size that remain are the state table and the compressed transition table. When a transition for a symbol is not found in the transition table, a default transition to a special dead state is used. When a machine blocks in the dead state, it does not recognize its input.
After a finite state machine is constructed, it is easy to generate a simple driver program that uses it to process input. Figure 7.9 contains an example of such a driver program. This program assumes the existence of a character class array like the one in Figure 7.2, except that it has only three character classes: one for digits, one for letters, and one for everything else (called delimiters). It also assumes there is a character case conversion array like the one in Figure 7.2. The driver takes a machine constructed using the code in Figure 7.7, and uses it to filter all stopwords, returning only legitimate index terms. It filters numbers, but accepts terms containing digits. It also converts the case of index terms.
Once the finite state machine blocks in the dead state, the string is not recognized. The driver program takes advantage of this fact by not running the finite state machine once it enters the dead state.
A lexical analyzer generator program can use these components in several ways. A lexical analyzer can be generated at indexing time, or ahead of time and stored in a file. The input can be read from a stream, as in the example driver program, or from another input source. A lexical analyzer data structure can be defined, and different stoplists and lexical analysis rules used in each one, then different analyzers can be run on different sorts of data. All these alternatives are easy to implement once the basic finite state machine generator and driver generator programs are in place.
As an illustration, Figure 7.10 contains the main function for a program that reads a stoplist from a file, builds a finite state machine using the function from Figure 7.8, then uses the driver function from Figure 7.9 to generate and print all the terms in an input file, filtering out the words in the stoplist.
Lexical analyzers built using the method outlined here can be constructed quickly, and are small and fast. For example, the finite state machine generated by the code in Figure 7.8 for the stoplist of 425 words in Figure 7.5 has only 318 states and 555 arcs. The program in Figure 7.10 built this finite state machine from scratch, then used it to lexically analyze the text from this chapter in under 1 second on a Sun SparcStation 1.
Lexical analysis must be done in automatic indexing and in query processing. Important decisions about the lexical form of indexing and query terms, and of query operators and grouping indicators, must be made in the design phase based on characteristics of databases and uses of the target system. Once this is done, it is a simple matter to apply techniques from program translation to the problem of lexical analysis. Finite state machine based lexical analyzers can be built quickly and reliably by hand or with a lexical analyzer generator.
Problems in the selection of stoplist words for automatic indexing are similar to those encountered in designing lexical analyzers, and likewise depend on the characteristics of the database and the system. Removing stoplist words during automatic indexing can be treated like a search problem, or can be incorporated into the lexical analysis process. Although hashing can be used to solve the searching problem very efficiently, it is probably best to incorporate stoplist processing into lexical analysis. Since stoplists may be large, automatic generation of lexical analyzers is the preferred approach in this case.
AHO, A., and M. CORASICK. 1975. "Efficient String Matching: An Aid to Bibliographic Search." Communications of the ACM, 18(6), 333-40.
AHO, A., R. SETHI, and J. ULLMAN. 1986. Compilers: Principles, Techniques, and Tools. New York: Addison-Wesley.
FOX, C. 1990. "A Stop List for General Text." SIGIR Forum, 24(1-2), 19-35.
FRANCIS, W., and H. KUCERA. 1982. Frequency Analysis of English Usage. New York: Houghton Mifflin.
HOPCROFT, J., and J. ULLMAN. 1979. Introduction to Automata Theory, Languages, and Computation. New York: Addison-Wesley.
LESK, M. 1975. Lex-A Lexical Analyzer Generator. Murray Hill, N.J.: AT&T Bell Laboratories.
LUHN, H. P. 1957. "A Statistical Approach to Mechanized Encoding and Searching of Literary Information. IBM Journal of Research and Development, 1(4).
SALTON, G., and M. MCGILL. 1983. Modern Information Retrieval. New York: McGraw-Hill.
TREMBLAY, J. P., and P. SORENSON. 1984. An Introduction to Data Structures with Applications, Second Edition. New York: McGraw-Hill.
VAN RIJSBERGEN, C. J. 1975. Information Retrieval. London: Butterworths.
WAIT, W. 1986. "The Cost of Lexical Analysis." Software Practice and Experience, 16(5), 473-88.
7.2 LEXICAL ANALYSIS
7.2.1 Lexical Analysis for Automatic Indexing
 Digits--Most numbers do not make good index terms, so often digits are not included as tokens. However, certain numbers in some kinds of databases may be important (for example, case numbers in a legal database). Also, digits are often included in words that should be index terms, especially in databases containing technical documents. For example, a database about vitamins would contain important tokens like "B6" and "B12." One partial (and easy) solution to the last problem is to allow tokens to include digits, but not to begin with a digit.
Digits--Most numbers do not make good index terms, so often digits are not included as tokens. However, certain numbers in some kinds of databases may be important (for example, case numbers in a legal database). Also, digits are often included in words that should be index terms, especially in databases containing technical documents. For example, a database about vitamins would contain important tokens like "B6" and "B12." One partial (and easy) solution to the last problem is to allow tokens to include digits, but not to begin with a digit. Hyphens--Another difficult decision is whether to break hyphenated words into their constituents, or to keep them as a single token. Breaking hyphenated terms apart helps with inconsistent usage (e.g., "state-of-the-art" and "state of the art" are treated identically), but loses the specificity of a hyphenated phrase. Also, dashes are often used in place of ems, and to mark a single word broken into syllables at the end of a line. Treating dashes used in these ways as hyphens does not work. On the other hand, hyphens are often part of a name, such as "Jean-Claude," "F-16," or "MS-DOS."
Hyphens--Another difficult decision is whether to break hyphenated words into their constituents, or to keep them as a single token. Breaking hyphenated terms apart helps with inconsistent usage (e.g., "state-of-the-art" and "state of the art" are treated identically), but loses the specificity of a hyphenated phrase. Also, dashes are often used in place of ems, and to mark a single word broken into syllables at the end of a line. Treating dashes used in these ways as hyphens does not work. On the other hand, hyphens are often part of a name, such as "Jean-Claude," "F-16," or "MS-DOS." Other Punctuation--Like the dash, other punctuation marks are often used as parts of terms. For example, periods are commonly used as parts of file names in computer systems (e.g., "COMMAND.COM" in DOS), or as parts of section numbers; slashes may appear as part of a name (e.g., "OS/2"). If numbers are regarded as legitimate index terms, then numbers containing commas and decimal points may need to be recognized. The underscore character is often used in terms in programming languages (e.g., "max_size" is an identifier in Ada, C, Prolog, and other languages).
Other Punctuation--Like the dash, other punctuation marks are often used as parts of terms. For example, periods are commonly used as parts of file names in computer systems (e.g., "COMMAND.COM" in DOS), or as parts of section numbers; slashes may appear as part of a name (e.g., "OS/2"). If numbers are regarded as legitimate index terms, then numbers containing commas and decimal points may need to be recognized. The underscore character is often used in terms in programming languages (e.g., "max_size" is an identifier in Ada, C, Prolog, and other languages). Case--The case of letters is usually not significant in index terms, and typically lexical analyzers for information retrieval systems convert all characters to either upper or lower case. Again, however, case may be important in some situations. For example, case distinctions are important in some programming languages, so an information retrieval system for source code may need to preserve case distinctions in generating index terms.
Case--The case of letters is usually not significant in index terms, and typically lexical analyzers for information retrieval systems convert all characters to either upper or lower case. Again, however, case may be important in some situations. For example, case distinctions are important in some programming languages, so an information retrieval system for source code may need to preserve case distinctions in generating index terms.7.2.2 Lexical Analysis for Query Processing
7.2.3 The Cost of Lexical Analysis
7.2.4 Implementing a Lexical Analyzer
 Use a lexical analyzer generator, like the UNIX tool lex (Lesk 1975), to generate a lexical analyzer automatically;
Use a lexical analyzer generator, like the UNIX tool lex (Lesk 1975), to generate a lexical analyzer automatically; Write a lexical analyzer by hand ad hoc; or
Write a lexical analyzer by hand ad hoc; or Write a lexical analyzer by hand as a finite state machine.
Write a lexical analyzer by hand as a finite state machine.
Figure 7.1: Transition diagram for a query lexical analyzer
/************** Character Classification *****************/
/* Tokenizing requires that ASCII be broken into character */
/* classes distinguished for tokenizing. White space */
/* characters separate tokens. Digits and letters make up */
/* the body of search terms. Parentheses group sub- */
/* expressions. The ampersand, bar, and caret are */
/* operator symbols. */
typedef enum {WHITE_CH, /* whitespace characters */
DIGIT_CH, /* the digits */
LETTER_CH, /* upper and lower case */
LFT_PAREN_CH, /* the "(" character */RGT_PAREN_CH, /* the ")" character */
AMPERSAND_CH, /* the "&" character */
BAR_CH, /* the "|" character */
CARET_CH, /* the "^" character */
EOS_CH, /* the end of string character */
OTHER_CH, /* catch-all for everything else */
} CharClassType;
static CharClassType char_class[128] = {/* ^@ */ EOS_CH, /* ^A */ OTHER_CH, /* ^B */ OTHER_CH,
/* ^C */ OTHER_CH, /* ^D */ OTHER_CH, /* ^E */ OTHER_CH,
/* ^F */ OTHER_CH, /* ^G */ OTHER_CH, /* ^H */ WHITE_CH,
/* ^I */ WHITE_CH, /* ^J */ WHITE_CH, /* ^K */ WHITE_CH,
/* ^L */ WHITE_CH, /* ^M */ WHITE_CH, /* ^N */ OTHER_CH,
/* ^O */ OTHER_CH, /* ^P */ OTHER_CH, /* ^Q */ OTHER_CH,
/* ^R */ OTHER_CH, /* ^S */ OTHER_CH, /* ^T */ OTHER_CH,
/* ^U */ OTHER_CH, /* ^V */ OTHER_CH, /* ^W */ OTHER_CH,
/* ^X */ OTHER_CH, /* ^Y */ OTHER_CH, /* ^Z */ OTHER_CH,
/* ^[ */ OTHER_CH, /* ^\ */ OTHER_CH, /* ^] */ OTHER_CH,
/* ^^ */ OTHER_CH, /* ^_ */ OTHER_CH, /* */ WHITE_CH,
/* ! */ OTHER_CH, /* " */ OTHER_CH, /* # */ OTHER_CH,
/* $ */ OTHER_CH, /* % */ OTHER_CH, /* & */ AMPERSAND_CH,
/* ' */ OTHER_CH, /* ( */ LFT_PAREN_C, /* ) */ RGT_PAREN_CH,
/* * */ OTHER_CH, /* + */ OTHER_CH, /* , */ OTHER_CH,
/* - */ OTHER_CH, /* . */ OTHER_CH, /* / */ OTHER_CH,
/* 0 */ DIGIT_CH, /* 1 */ DIGIT_CH, /* 2 */ DIGIT_CH,
/* 3 */ DIGIT_CH, /* 4 */ DIGIT_CH, /* 5 */ DIGIT_CH,
/* 6 */ DIGIT_CH, /* 7 */ DIGIT_CH, /* 8 */ DIGIT_CH,
/* 9 */ DIGIT_CH, /* : */ OTHER_CH, /* ; */ OTHER_CH,
/* < */ OTHER_CH, /* = */ OTHER_CH, /* > */ OTHER_CH,
/* ? */ OTHER_CH, /* @ */ OTHER_CH, /* A */ LETTER_CH,
/* B */ LETTER_CH, /* C */ LETTER_CH, /* D */ LETTER_CH,
/* E */ LETTER_CH, /* F */ LETTER_CH, /* G */ LETTER_CH,
/* H */ LETTER_CH, /* I */ LETTER_CH, /* J */ LETTER_CH,
/* K */ LETTER_CH, /* L */ LETTER_CH, /* M */ LETTER_CH,
/* N */ LETTER_CH, /* O */ LETTER_CH, /* P */ LETTER_CH,
/* Q */ LETTER_CH, /* R */ LETTER_CH, /* S */ LETTER_CH,
/* T */ LETTER_CH, /* U */ LETTER_CH, /* V */ LETTER_CH,
/* W */ LETTER_CH, /* X */ LETTER_CH, /* Y */ LETTER_CH,
/* Z */ LETTER_CH, /* [ */ OTHER_CH, /* \ */ OTHER_CH,
/* ] */ OTHER_CH, /* ^ */ CARET_CH, /* _ */ OTHER_CH,
/* ` */ OTHER_CH, /* a */ LETTER_CH, /* b */ LETTER_CH,
/* c */ LETTER_CH, /* d */ LETTER_CH, /* e */ LETTER_CH,
/* f */ LETTER_CH, /* g */ LETTER_CH, /* h */ LETTER_CH,
/* i */ LETTER_CH, /* j */ LETTER_CH, /* k */ LETTER_CH,
/* l */ LETTER_CH, /* m */ LETTER_CH, /* n */ LETTER_CH,
/* o */ LETTER_CH, /* p */ LETTER_CH, /* q */ LETTER_CH,
/* r */ LETTER_CH, /* s */ LETTER_CH, /* t */ LETTER_CH,
/* u */ LETTER_CH, /* v */ LETTER_CH, /* w */ LETTER_CH,
/* x */ LETTER_CH, /* y */ LETTER_CH, /* z */ LETTER_CH,
/* { */ OTHER_CH, /* | */ BAR_CH, /* } */ OTHER_CH,/* */ OTHER_CH, /* ^? */ OTHER_CH, };
/************** Character Case Conversion *************/
/* Term text must be accumulated in a single case. This */
/* array is used to convert letter case but otherwise */
/* preserve characters. */
static char convert_case[128] = {/* ^@ */ 0, /* ^A */ 0, /* ^B */ 0, /* ^C */ 0,
/* ^D */ 0, /* ^E */ 0, /* ^F */ 0, /* ^G */ 0,
/* ^H */ 0, /* ^I */ 0, /* ^J */ 0, /* ^K */ 0,
/* ^L */ 0, /* ^M */ 0, /* ^N */ 0, /* ^O */ 0,
/* ^P */ 0, /* ^Q */ 0, /* ^R */ 0, /* ^S */ 0,
/* ^T */ 0, /* ^U */ 0, /* ^V */ 0, /* ^W */ 0,
/* ^X */ 0, /* ^Y */ 0, /* ^Z */ 0, /* ^[ */ 0,
/* ^\ */ 0, /* ^] */ 0, /* ^^ */ 0, /* ^_ */ 0,
/* */ ' ', /* ! */ '!', /* " */ '"', /* # */ '#',
/* $ */ '$', /* % */ '%', /* & */ '&', /* ' */ ''',
/* ( */ '(', /* ) */ ')', /* * */ '*', /* + */ '+',/* , */ ',', /* - */ '-', /* . */ '.', /* / */ '/',
/* 0 */ '0', /* 1 */ '1', /* 2 */ '2', /* 3 */ '3',
/* 4 */ '4', /* 5 */ '5', /* 6 */ '6', /* 7 */ '7',
/* 8 */ '8', /* 9 */ '9', /* : */ ':', /* ; */ ';',
/* < */ '<', /* = */ '=', /* > */ '>', /* ? */ '?',
/* @ */ '@', /* A */ 'a', /* B */ 'b', /* C */ 'c',
/* D */ 'd', /* E */ 'e', /* F */ 'f', /* G */ 'g',
/* H */ 'h', /* I */ 'i', /* J */ 'j', /* K */ 'k',
/* L */ 'l', /* M */ 'm', /* N */ 'n', /* O */ o',
/* P */ 'p', /* Q */ 'q', /* R */ 'r', /* S */ 's',
/* T */ 't', /* U */ 'u', /* V */ 'v', /* W */ 'w',
/* X */ 'x', /* Y */ 'y', /* Z */ 'z', /* [ */ '[',
/* \ */ '\', /* ] */ ']', /* ^ */ '^', /* _ */ '_',
/* ` */ '`', /* a */ 'a', /* b */ 'b', /* c */ 'c',
/* d */ 'd', /* e */ 'e', /* f */ 'f', /* g */ 'g',
/* h */ 'h', /* i */ 'i', /* j */ 'j', /* k */ 'k',
/* l */ 'l', /* m */ 'm', /* n */ 'n', /* o */ 'o',
/* p */ 'p', /* q */ 'q', /* r */ 'r', /* s */ 's',
/* t */ 't', /* u */ 'u', /* v */ 'v', /* w */ 'w',
/* x */ 'x', /* y */ 'y', /* z */ 'z', /* { */ '{' ,/* | */ '|', /* } */ '}', /* ~ */ '~', /* ^? */ 0, };
/******************** Tokenizing ***********************/
/* The lexer distinguishes terms, parentheses, the and, or */
/* and not operators, the unrecognized token, and the end */
/* of the input. */
typedef enum {TERM_TOKEN = 1, /* a search term */
LFT_PAREN_TOKEN = 2, /* left parenthesis */
RGT_PAREN_TOKEN = 3, /* right parenthesis */
AND_TOKEN = 4, /* set intersection connective */
OR_TOKEN = 5, /* set union connective */
NOT_TOKEN = 6, /* set difference connective */
END_TOKEN = 7, /* end of the query */
NO_TOKEN = 8, /* the token is not recognized */
} TokenType;
Figure 7.2: Declarations for a simple query lexical analyzer
/*FN************************************************************************
GetToken( stream )
Returns: void
Purpose: Get the next token from an input stream
Plan: Part 1: Run a state machine on the input
Part 2: Coerce the final state to return the token type
Notes: Run a finite state machine on an input stream, collecting
the text of the token if it is a term. The transition table
for this DFA is the following (negative states are final):
State | White Letter ( ) & | ^ EOS Digit Other
-------------------------------------------------------------
0 | 0 1 -2 -3 -4 -5 -6 -7 -8 -8
1 | -1 1 -1 -1 -1 -1 -1 -1 1 -1
See the token type above to see what is recognized in the
various final states.
**/
static TokenType
GetToken( stream, term )
FILE *stream; /* in: where to grab input characters */
char *term; /* out: the token text if the token is a term */
{int next_ch; /* from the input stream */
int state; /* of the tokenizer DFA */
int i; /* for scanning through the term buffer */
/* Part 1: Run a state machine on the input */
state = 0;
i = 0;
while ( 0 < = state )
{if ( EOF == (next_ch = getc(stream)) ) next_ch = '\0';
term[i++] = convert_case[next_ch];
switch( state )
{case 0 :
switch( char_class[next_ch] )
{case WHITE_CH : i = 0; break;
case LETTER_CH : state = 1; break;
case LFT_PAREN_CH : state = -2; break;
case RGT_PAREN_CH : state = -3; break;
case AMPERSAND_CH : state = -4; break;
case BAR_CH : state = -5; break;
case CARET_CH : state = -6; break;
case EOS_CH : state = -7; break;
case DIGIT_CH : state = -8; break;
case OTHER_CH : state = -8; break;
default : state =-8; break;
}
break;
case 1 :
if ( (DIGIT_CH != char_class[next_ch])
&& (LETTER_CH != char_class[next_ch]) )
{ungetc( next_ch, stream );
term[i-1] = '\0';
state = -1;
}
break;
default : state = -8; break;
}
}
/* Part 2: Coerce the final state to return the type token */
return( (TokenType) (-state) );
} /* GetToken */
Figure 7.3: Code for a simple query lexical analyzer
/*FN***********************************************************************
main( argc, argv )
Returns: int -- 0 on success, 1 on failure
Purpose: Program main function
Plan: Part 1: Open a file named on the command line
Part 2: List all the tokens found in the file
Part 3: Close the file and return
Notes: This program simply lists the tokens found in a single file
named on the command line.
**/
int
main(argc, argv)
int argc; /* in: how many arguments */
char *argv[ ] /* in: text of the arguments */
{TokenType token; /* next token in the input stream */
char term[128]; /* the term recognized */
FILE *stream; /* where to read the data from */
if ( (2 != argc) || !(stream = fopen(argv[l],"r")) ) exit(l);
do
switch( token = GetToken(stream,term) )
{case TERM_TOKEN : (void)printf ( "term: %s\n", term ); break;
case LFT_PAREN_TOKEN : (void)printf ( "left parenthesis\n" ); break;
case RGT PAREN-TOKEN : (void)printf ( "right parenthesis\n" ); break;
case AND_TOKEN : (void)printf ( "and operator\n" ); break;
case OR_TOKEN : (void)printf ( "or operator\n" ); break;
case NOT_TOKEN : (void)printf ( "not operator\n" ); break;
case END_TOKEN : (void)printf ( "end of string\n" ); break;
case NO_TOKEN : (void)printf ( "no token\n" ); break;
default : (void)printf ( "bad data\n" ); break;
}
while ( END_TOKEN != token );
fclose ( stream );
} /* main */
Figure 7.4: Test program for a query lexical analyzer
7.3 STOPLISTS
a about above across after
again against all almost alone
along already also although always
among an and another any
anybody anyone anything anywhere are
area areas around as ask
asked asking asks at away
b back backed backing backs
be because became become becomes
been before began behind being
beings best better between big
both but by c came
can cannot case cases certain
certainly clear clearly come could
d did differ different differently
do does done down downed
downing downs during e each
early either end ended ending
ends enough even evenly ever
every everybody everyone everything everywhere
f face faces fact facts
far felt few find finds
first for four from full
fully further furthered furthering furthers
g gave general generally get
gets give given gives go
going good goods got great
greater greatest group grouped grouping
groups h had has have
having he her herself here
high higher highest him himself
his how however i if
important in interest interested interesting
interests into is it its
itself j just k keep
keeps kind knew know known
knows l large largely last
later latest least less let
lets like likely long longer
longest m made make making
man many may me member
members men might more most
mostly mr mrs much must
my myself n necessary need
needed needing needs never new
newer newest next no non
not nobody noone nothing now
nowhere number numbered numbering numbers
o of off often old
older oldest on once one
only open opened opening opens
or order ordered ordering orders
other others our out over
p part parted parting parts
per perhaps place places point
pointed pointing points possible present
presented presenting presents problem problems
put puts q quite r
rather really right room rooms
s said same saw say
says second seconds see seem
seemed seeming seems sees several
shall she should show showed
showing shows side sides since
small smaller smallest so some
somebody someone something somewhere state
states still such sure t
take taken than that the
their them then there therefore
these they thing things think
thinks this those though thought
thoughts three through thus to
today together too took toward
turn turned turning turns two
u under until up upon
us use uses used v
very w want wanted wanting
wants was way ways we
well wells went were what
when where whether which while
who whole whose why will
with within without work worked
working works would x y
year years yet you young
younger youngest your yours z
Figure 7.5: A stoplist for general text
7.3.1 Implementing Stoplists
7.3.2 A Lexical Analyzer Generator
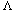 }, the transition on i to a state labeled {n, nto}, and the transition on t to a state labeled {o}. A state label L labeling a target state for a transition on symbol a is called a derivative label L with transition a. A state is made a final state if and only if its label contains the empty string.
}, the transition on i to a state labeled {n, nto}, and the transition on t to a state labeled {o}. A state label L labeling a target state for a transition on symbol a is called a derivative label L with transition a. A state is made a final state if and only if its label contains the empty string.create an initial state qo and label it with the input set Lo;
place qo in a state queue Q;
while Q is not empty do:
{remove state qi from Q;
generate the derivative state labels from the label Li for qi;
for each derivative state label Lj with transition a:
{if no state qj labelled Lj exists, create qj and put it in Q;
create an arc labelled a from qi to qj;
}
}
make all states whose label contains
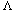 final states.
final states.Figure 7.6: Algorithm for generating a finite state machine

Figure 7.7: An example of a generated finite state machine
#define DEAD_STATE -1 /* used to block a DFA */
#define TABLE_INCREMENT 256 /* used to grow tables */
/************************* Hashing ****************************/
/* Sets of suffixes labeling states during the DFA construction */
/* are hashed to speed searching. The hashing function uses an */
/* entire integer variable range as its hash table size; in an */
/* effort to get a good spread through this range, hash values */
/* start big, and are incremented by a lot with every new word */
/* in the list. The collision rate is low using this method. */
#define HASH_START 5775863
#define HASH_INCREMENT 38873647
/************** State Label Binary Search Tree ****************/
/* During DFA construction, all states must be searched by */
/* their labels to make sure that the minimum number of states */
/* are used. This operation is sped up by hashing the labels */
/* to a signature value, then storing the signatures and labels */
/* in a binary search tree. The tree is destroyed once the DFA */
/* is fully constructed. */
typedef struct TreeNode {StrList label; /* state label used as search key */
unsigned signature; /* hashed label to speed searching */
int state; /* whose label is representd by node */
struct TreeNode *left; /* left binary search subtree */
struct TreeNode *right; /* right binary search subtree */
} SearchTreeNode, *SearchTree;
/********************* DFA State Table ************************/
/* The state table is an array of structures holding a state */
/* label, a count of the arcs out of the state, a pointer into */
/* the arc table for these arcs, and a final state flag. The */
/* label field is used only during machine construction. */
typedef struct {StrList label; /* for this state - used during build */
int num_arcs; /* for this state in the arc table */
int arc_offset; /* for finding arcs in the arc table */
short is_final; /* TRUE iff this is a final state */
} StateTableEntry, *StateTable;
/********************** DFA Arc Table *************************/
/* The arc table lists all transitions for all states in a DFA */
/* in compacted form. Each state's transitions are offset from */
/* the start of the table, then listed in arc label order. */
/* Transitions are found by a linear search of the sub-section */
/* of the table for a given state. */
typedef struct {char label; /* character label on an out-arrow */
int target; /* the target state for the out-arrow */
} ArcTableEntry, *ArcTable;
********************** DFA Structure *********************** /
/* A DFA is represented as a pointer to a structure holding the */
/* machine's state and transition tables, and bookkeepping */
/* counters. The tables are arrays whose space is malloc'd, */
/* then realloc'd if more space is required. Once a machine is */
/* constructed, the table space is realloc'd one last time to */
/* fit the needs of the machine exactly. */
typedef struct {int num_states; /* in the DFA (and state table) */
int max_states; /* now allocated in the state table */
int num_arcs; /* in the arc table for this machine */
int max_arcs; /* now allocated in the arc table */
StateTable state_table; /* the compacted DFA state table */
ArcTable arc_table; /* the compacted DFA transition table */
SearchTree tree; /* storing state labels used in build */
} DFAStruct, *DFA;
/*FN**************************************************************************
DestroyTree( tree )
Returns: void
Purpose: Destroy a binary search tree created during machine construction
Plan: Part 1: Return right away of there is no tree
Part 2: Deallocate the subtrees
Part 3: Deallocate the root
Notes: None.
**/
static void
DestroyTree( tree )
SearchTree tree; /* in: search tree destroyed */
{/* Part 1: Return right away of there is no tree */
if ( NULL == tree ) return;
/* Part 2: Deallocate the subtrees */
if ( NULL != tree->left ) DestroyTree ( tree->left );
if ( NULL != tree->right ) DestroyTree ( tree->right );
/* Part 3: Deallocate the root */
tree->left = tree->right = NULL;
(void)free( (char *)tree );
} /* DestroyTree */
/*FN************************************************************************
GetState( machine, label, signature )
Returns: int -- state with the given label
Purpose: Search a machine and return the state with a given state label
Plan: Part 1: Search the tree for the requested state
Part 2: If not found, add the label to the tree
Part 3: Return the state number
Notes: This machine always returns a state with the given label
because if the machine does not have a state with the given
label, then one is created.
**/
static int
GetState(machine, label, signature)
DFA machine; /* in: DFA whose state labels are searched;
StrList label; /* in: state label searched for */
unsigned signature; /* in: signature of the label requested */
{SearchTree *ptr; /* pointer to a search tree link field */
SearchTree new_node; /* for a newly added search tree node */
/* Part 1: Search the tree for the requested state */
ptr = &(machine->tree);
while ( (NULL != *ptr) && ( (signature != (*ptr)->signature)
|| !StrListEqual(label,(*ptr)->label)) )
ptr = (signature <= (*ptr)->signature) ? &(*ptr)->left : &(*ptr)->right;
/* Part 2: If not found, add the label to the tree */
if ( NULL == *ptr )
{/* create a new node and fill in its fields */
new_node = (SearchTree)GetMemory( NULL, sizeof(SearchTreeNode) );
new-node->signature = signature;
new_node->label = (StrList)label;
new_node->state = machine->num_states;
new_node->left = new_node->right = NULL;
/* allocate more states if needed, set up the new state */
if ( machine->num_states == machine->max_states )
{machine->max_states += TABLE_INCREMENT;
machine->state_table =
(StateTable)GetMemory(machine-state_table,
machine-max_states*sizeof(StateTableEntry));
}
machine->state_table[machine-num_states].label = (StrList)label;
machine->num_states++;
/* hook the new node into the binary search tree */
*ptr = new_node;
}
else
StrListDestroy( label );
/* Part 3: Return the state number */
return( (*ptr)->state );
} /* GetState */
/*FN*********************************************************************************
AddArc( machine, state, arc_label, state_label, state_signature )
Returns: void
Purpose: Add an arc between two states in a DFA
Plan: Part 1: Search for the target state among existing states
Part 2: Make sure the arc table is big enough
Part 3: Add the new arc
Notes: None.
**/
static void
AddArc( machine, state, arc_label, state_label, state_signature )
DFA machine; /* in/out: machine with an arc added */
int state; /* in: with an out arc added */
char arc_label; /* in: label on the new arc */
StrList state_label; /* in: label on the target state */
unsigned state_signature; /* in: label hash signature to speed searching */
{register int target; /* destination state for the new arc */
/* Part 1: Search for the target state among existing states */
StrListSort( 0, state_label );
target = GetState( machine, state_label, state_signature );
/* Part 2: Make sure the arc table is big enough */
if ( machine->num_arcs == machine->max_arcs )
{machine->max_arcs += TABLE_INCREMENT;
machine->arc_table =
(ArcTable)GetMemory( machine->arc_table,
machine->max_arcs * sizeof(ArcTableEntry) );
}
/* Part 3: Add the new arc */
machine->arc_table[machine->num_arcs].label = arc_label;
machine->arc_tablel[machine->num_arcs].target = target;
machine->num_arcs++;
machine->state_table[state].num_arcs++;
} /* AddArc */
/*FN**********************************************************************************
BuildDFA( words )
Returns: DFA -- newly created finite state machine
Purpose: Build a DFA to recognize a list of words
Plan: Part 1: Allocate space and initialize variables
Part 2: Make and label the DFA start state
Part 3: Main loop - build the state and arc tables
Part 4: Deallocate the binary search tree and the state labels
Part 5: Reallocate the tables to squish them down
Part 6: Return the newly constructed DFA
Notes: None.
**/
DFA
BuildDFA( words )
StrList words; /* in: that the machine is built to recognize */
{DFA machine; /* local for easier access to machine */
register int state; /* current state's state number */
char arc_label; /* for the current arc when adding arcs */
char *string; /* element in a set of state labels */
char ch; /* the first character in a new string */
StrList current_label; /* set of strings labeling a state */
StrList target_label; /* labeling the arc target state */
unsigned target_signature; /* hashed label for binary search tree */
register int i; /* for looping through strings */
/* Part 1: Allocate space and initialize variables */
machine = (DFA)GetMemory( NULL, sizeof(DFAStruct) );
machine->max_states = TABLE_INCREMENT;
machine->state_table =
(StateTable)GetMemory(NULL, machine->max_states*sizeof(StateTableEntry));
machine->num_states = 0;
machine->max_arcs = TABLE_INCREMENT;
machine->arc_table =
(ArcTable)GetMemory ( NULL, machine->max_arcs * sizeof(ArcTableEntry) );
machine->num_arcs = 0;
machine->tree = NULL;
/* Part 2: Make and label the DFA start state */
StrListUnique( 0, words ); /* sort and unique the list */
machine->state_table[0].label = words;
machine->num_states = 1;
/* Part 3: Main loop - build the state and arc tables */
for ( state = 0; state < machine->num_states; state++ )
{/* The current state has nothing but a label, so */
/* the first order of business is to set up some */
/* of its other major fields */
machine->state_table[state].is_final = FALSE;
machine->state_table[state].arc_offset = machine->num_arcs;
machine->state_table[state].num_arcs = 0;
/* Add arcs to the arc table for the current state */
/* based on the state's derived set. Also set the */
/* state's final flag if the empty string is found */
/* in the suffix list */
current_label = machine->state_table[state].label;
target_label = StrListCreate();
target_signature = HASH_START;
arc_label = EOS;
for ( i = 0; i < StrListSize(current_label); i++ )
{/* get the next string in the label and lop it */
string = StrListPeek( current_label, i );
ch = *string++;
/* the empty string means mark this state as final */
if ( EOS == ch )
{ machine->state_table[state].is_final = TRUE; continue; }/* make sure we have a legitimate arc_label */
if ( EOS == arc_label ) arc_label = ch;
/* if the first character is new, then we must */
/* add an arc for the previous first character */
if ( ch != arc_label )
{AddArc (machine, state, arc_label, target_label, target_signature);
target_label = StrListCreate();
target_signature = HASH_START;
arc_label = ch;
}
/* add the current suffix to the target state label */
StrListAppend( target_label, string );
target_signature += (*string + l) * HASH_INCREMENT;
while ( *string ) target_signature += *string++;
}
/* On loop exit we have not added an arc for the */
/* last bunch of suffixes, so we must do so, as */
/* long as the last set of suffixes is not empty */
/* (which happens when the current state label */
/* is the singleton set of the empty string). */
if ( 0 < StrListSize(target_label) )
AddArc( machine, state, arc_label, target_label, target_signature );
}
/* Part 4: Deallocate the binary search tree and the state labels */
DestroyTree( machine->tree ); machine->tree = NULL;
for ( i = 0; i < machine->num_states; i++ )
{StrListDestroy( machine->state_table[i].label );
machine->state_table[i]. label = NULL;
}
/* Part 5: Reallocate the tables to squish them down */
machine->state_table = (StateTable)GetMemory( machine->state_table,
machine->num_states * sizeof(StateTableEntry) );
machine->arc_table = (ArcTable)GetMemory( machine->arc_table,
machine->num_arcs * sizeof(ArcTableEntry) );
/* Part 6: Return the newly constructed DFA */
return( machine );
} /* BuildDFA */
Figure 7.8: Code for DFA generation
/*FN*************************************************************************
GetTerm( stream, machine, size, output )
Returns: char * - - NULL if stream is exhausted, otherwise output buffer
Purpose: Get the next token from an input stream, filtering stop words
Plan: Part 1: Return NULL immediately if there is no input
Part 2: Initialize the local variables
Part 3: Main Loop: Put an unfiltered word into the output buffer
Part 4: Return the output buffer
Notes: This routine runs the DFA provided as the machine parameter,
and collects the text of any term in the output buffer. If
a stop word is recognized in this process, it is skipped.
Care is also taken to be sure not to overrun the output buffer.
**/
char *
GetTerm( stream, machine, size, output )
FILE *stream; /* in: source of input characters */
DFA machine; /* in: finite state machine driving process */
int size; /* in: bytes in the output buffer */
char *output; /* in/out: where the next token in placed */
{char *outptr; /* for scanning through the output buffer */
int ch; /* current character during input scan */
register int state; /* current state during DFA execution */
/* Part 1: Return NULL immediately if there is no input */
if ( EOF = = (ch = getc(stream)) ) return( NULL );
/* Part 2: Initialize the local variables */
outptr = output;
/* Part 3: Main Loop: Put an unfiltered word into the output buffer */
do
{/* scan past any leading delimiters */
while ( (EOF != ch ) &&
((DELIM_CH == char_class[ch]) | |
(DIGIT_CH == char_class[ch])) ) ch = getc( stream );
/* start the machine in its start state */
state = 0;
/* copy input to output until reaching a delimiter, and also */
/* run the DFA on the input to watch for filtered words */
while ( (EOF != ch) && (DELIM_CH != char_class[ch]) )
{if ( outptr == (output+size-1) ) { outptr = output; state = 0; }*outptr++ = convert_case[ch];
if ( DEAD_STATE != state )
{register int i; /* for scanning through arc labels */
int arc_start; /* where the arc label list starts */
int arc_end; /* where the arc label list ends */
arc_start = machine->state_table[state].arc_offset;
arc_end = arc_start + machine->state_table[state].num_arcs;
for ( i = arc_start; i < arc_end; i++ )
if ( convert_case[ch] == machine->arc_table[i].label )
{ state = machine->arc_table[i].target; break; }if ( i == arc_end ) state = DEAD_STATE;
}
ch = getc( stream );
}
/* start from scratch if a stop word is recognized */
if ( (DEAD_STATE != state) && machine->state_table[state].is_final )
outptr = output;
/* terminate the output buffer */
*outptr = EOS;
}
while ( (EOF != ch) && !*output );
/* Part 4: Return the output buffer */
return( output );
} /* GetTerm */
Figure 7.9: An example of DFA driver program
/*FN**************************************************************************
main( argc, argv )
Returns: int -- 0 on success, 1 on failure
Purpose: Program main function
Plan: Part 1: Read the stop list from the stop words file
Part 2: Create a DFA from a stop list
Part 3: Open the input file and list its terms
Part 4: Close the input file and return
Notes: This program reads a stop list from a file called "words.std,"
and uses it in generating the terms in a file named on the
command line.
**/
int
main( argc, argv )
int argc; /* in: how many arguments */
char *argv[]; /* in: text of the arguments */
{char term[128]; /* for the next term found */
FILE *stream; /* where to read characters from */
StrList words; /* the stop list filtered */
DFA machine; /* build from the stop list */
/* Part 1: Read the stop list from the stop words file */
words = StrListCreate( );
StrListAppendFile( words, "words.std" );
/* Part 2: Create a DFA from a stop list */
machine = BuildDFA( words );
/* Part 3: Open the input file and list its terms */
if ( !(stream = fopen(argv[1], "r")) ) exit(1);
while ( NULL != GetTerm(stream, machine, 128, term) )
(void)printf( "%s/n", term );
/* Part 4: Close the input file and return */
(void)fclose( stream );
return(0);
} /* main */
Figure 7.10: Main function for a term generator program
7.4 SUMMARY
REFERENCES


