Thinking Machines Corporation, 245 First Street, Cambridge, Massachusetts
Abstract
Data Parallel computers, such as the Connection Machine CM-2, can provide interactive access to text databases containing tens, hundreds, or even thousands of Gigabytes of data. This chapter starts by presenting a brief overview of data parallel computing, a performance model of the CM-2, and a model of the workload involved in searching text databases. The remainder of the chapter discusses various algorithms used in information retrieval and gives performance estimates based on the data and processing models just presented. First, three algorithms are introduced for determining the N highest scores in a list of M scored documents. Next, the parallel signature file representation is described. Two document scoring algorithms are fully described; a sketch of a boolean query algorithm are also presented. The discussion of signatures concludes with consideration of false hit rates, data compression, secondary/tertiary storage, and the circumstances under which signatures should be considered. The final major section discusses inverted file methods. Two methods, parallel inverted files and partitioned posting files, are considered in detail. Finally, issues relating to secondary storage are briefly considered.
The time required to search a text database is, in the limit, proportional to the size of the database. It stands to reason, then, that as databases grow they will eventually become so large that interactive response is no longer possible using conventional (serial) machines. At this point, we must either accept longer response times or employ a faster form of computer. Parallel computers are attractive in this respect: parallel machines exist which are up to four orders of magnitude faster than typical serial machines. In this chapter we will examine the data structure and algorithmic issues involved in harnessing this power.
In this chapter we are concerned with vector-model document ranking systems. In such systems, both documents and queries are modeled as vectors. At a superficial level, retrieval consists of (1) computing the dot-product of the query vector with every document vector; and (2) determining which documents have the highest scores. In practice, of course, both document and query vectors are extremely sparse; coping with this sparseness lies at the heart of the design of practical scoring algorithms.
The organization of the chapter is as follows. First, we will describe the notation used to describe parallel algorithms, and present a timing model for one parallel computer, the Connection Machinel\®System model CM-2
1Connection Machine\® is a registered trademark of Thinking Machines Corporation. C*\® is a registered trademark of Thinking Machines Corporation. CM-2
2This topic is presented first because certain aspects of document scoring will be difficult to understand if the data arrangements convenient to document ranking have not yet been presented.
The algorithms fpresented in this chapter utilize the data parallel computing model proposed by Hillis and Steele (1986). In this model, there is a single program that controls a large number of processing elements, each of which will be performing the same operation at any moment. Parallelism is expressed by the creation of parallel data structures and the invocation of parallel operators. The model is made manifest in data parallel programming languages, such as the C* language developed by Thinking Machines Corporation (1990). The body of this section presents some basic data structures, operators, and notations which will be required to understand the algorithms presented in the remainder of the chapter. The section will conclude with a concise performance model for one implementation of the data parallel model (the Connection Machine model CM-2). More details on the architecture of this machine are provided by Hillis (1985) and Thinking Machines Corporation (1987).
Data types are implicit in the algorithmic notation presented below. In general, scalar variables are lowercase, for example, i. Scalar constants are all uppercase, for example, N_PROCS. Parallel integer-valued variables are prefixed with P_, e.g. P_x. Parallel Boolean-valued variables are prefixed with B_. Other aspects of data type, such as underlying structure and array declarations, will be left implicit and may be deduced by reading the accompanying text.
C* includes all the usual C data structures and operations. These are called scalar variables and scalar operations.
A shape may be thought of as an array of processors. Each element of a shape is referred to as a position. A parallel variable is defined by a base type and a shape. It can be thought of as a vector having one element per position in the shape. A parallel variable can store one value at each of its positions. For example, if P is defined in a shape with 8 positions, it will have storage for 8 different values. When we display the contents of memory in the course of describing data structures and algorithms, variables will run from top to bottom and positions will run from left to right. Thus, if we have two variables, P_1 and P_2, we might display them as follows:
Individual values of a parallel variable are obtained by left indexing: element 4 of P_1 is referenced as [4] P_1, and has a value of 9. All indexing is zero-based.
There is a globally defined parallel variable, P_position, which contains 0 in position 0, l in position 1, and so on.
It is also possible to have parallel arrays. For example, P_array might be a parallel variable of length 3:
Array subscripting (right indexing) is done as usual; element 1 of P_array would be referred to as P_array [1], and would be a parallel integer having 8 positions. Left and right indexing may be combined, so that the 4'th position of the 0'th element of P_array would be referred to as [4] P_array[0], and have the value of 30.
Each scalar arithmetic operator (+, *, etc.) has a vector counterpart that is applied elementwise to its operands. For example, the following line of code multiplies each element of P_x by the corresponding element of P_y, then the stores the result in P_z:
This might result in the following data store:
At any moment, a given shape has a set of active positions. All positions are initially active. Parallel operations, such as arithmetic and assignment, take effect only at active positions. The set of active positions may be altered by using the where statement, which is a parallel analogue to the scalar if statement. The where statement first evaluates a test. The body will then be executed with the active set restricted to those positions where the test returned nonzero results. The else clause, if present, will then be executed wherever the test returned 0. For example, the following computes the smaller of two numbers:
Everything mentioned up to this point involves the simple extension of scalar data structures and operations to vector data structures and element-wise vector operations. We will now consider some basic operations that involve operating on data spread across multiple positions; these are collectively referred to as nonlocal operations.
The simplest of these operations are the global reduction operations. These operations compute cumulative sums, cumulative minima/maxima, and cumulative bitwise AND/ORs across all active positions in a shape. The following unary operators are used to stand for the global reduction operators:
Suppose, for example, we wish to compute the arithmetic mean of P_x. This may be done by computing the cumulative sum of P_x and dividing it by the number of active positions. This second quantity can be computed by finding the cumulative sum (over all active positions) of 1:
mean = (+= P_x) / (+= 1);
Parallel left-indexing may be used to send data from one position to another. In this operation, it is useful to think of each position in a shape as corresponding to a processor. When it sees an expression such as [P_i] P_y = P_x, it will send its value of P_x to position P_i, and store it in P_y. For example, one might see the following:
In the event that multiple positions are sending data to the same destination, conflicts may be resolved by arbitrarily choosing one value, by choosing the largest/ smallest value, by adding the values, or by taking the bitwise AND/OR of the values. These different methods of resolving collisions are specified by using one of the following binary operatores:3
These are binary forms of the global reduce operations introduced above.
3These are referred to as the send-reduce operators.
The final group of nonlocal operations to be considered here are called scan operations, and are used to compute running sums, running maxima/minima, and running bitwise AND/OR's. In it simplest form, scan_with_add will take a parallel variable and return a value which, at a given position, is the cumulative sum of all positions to its left, including itself. For example:
Optionally, a Boolean flag (called a segment flag) may be supplied. Wherever this flag is equal to 1, it causes the running total to be reset to 0. For example:
We will now consider the performance of one parallel computer, the Connection Machine model CM-2. In scalar C, the various primitive operators such as + and = have fairly uniform time requirements. On parallel computers, however, different operators may have vastly differing time requirements. For example, adding two parallel variables is a purely local operation, and is very fast. Parallel left-indexing, on the other hand, involves moving data from one processor to another, and is two orders of magnitude slower.
In addition, any realization of this model must take into account the fact that a given machine has a finite number of processing elements and, if a shape becomes large enough, several positions will map to the same physical processor. We call the ratio of the number of positions in a shape to the number of physical processors the virtual processing ratio (VP ratio). As the VP ratio increases, each processor must do the work of several and, as a first approximation, a linear increase in running time will be observed.
The following symbols will be used:
We express the time required for each operator by an equation of the form c1 + c2r. For example, if an operator takes time 2 + 10r, then it will take 12 microseconds at a VP ratio of 1, 22 microseconds at a VP ratio of 2, and so forth. For convenience, we will also include the time required for an operator at a VP ratio of 1. On the CM-2, the time required for scalar operations is generally insignificant and will be ignored.
To arrive at a time estimate for an algorithm, we first create an algorithm skeleton in which all purely scalar operations except for looping are eliminated, and all identifiers are replaced with P for parallel integers, B for parallel Booleans, and S for scalars. Loop constructs will be replaced by a simple notation of the form loop (count) . All return statements will be deleted. Assignment statements which might reasonably be eliminated by a compiler will be suppressed. Finally, because the cost of scalar right-indexing is zero, all instances of P [S] will be replaced with P. From this skeleton, the number of times each parallel operator is called may be determined. The time requirements are then looked up in a table provided at the end of this section, and an estimate constructed.
For example, suppose we have a parallel array of length N and wish to find the sum of its elements across all positions. The algorithm for this is as follows:
This has the skeleton:
It requires time:
The following timing equations characterize the performance of the CM-2.4
4Throughout this chapter, all times are in microseconds unless noted otherwise.
18.3 A MODEL OF THE RETRIEVAL TASK
Retrieval consists of (1) scoring documents, and (2) determining which documents received the highest scores. This second step--ranking--will be considered first. Any of the ranking algorithms discussed below may be used in combination with any of the scoring algorithms which will be discussed later. It should be noted that, while scoring is probably the more interesting part of the retrieval process, ranking may be a large portion of the overall compute cost, and ranking algorithms are as deserving of careful design as are scoring algorithms.
The problem may be stated as follows: given a set of Ndocs integers (scores), identify the Nret highest-ranking examples. The scores may be stored in one of two formats: with either one score per position, or with an array of Nrows scores per position. The former case involves a VP ratio
The second case, assuming a VP ratio of one is used, requires an array of size
We will assume there is a fast method for converting a parallel variable at a VP ratio of r to a parallel array having Nrows cells per processor. Such a function is, in fact, provided on the Connection Machine; it requires essentially zero time.
Many parallel computing systems provide a parallel ranking routine which, given a parallel integer, returns 0 for the largest integer, 1 for the next largest, and so forth.5 This may be used to solve the problem quite directly: one finds the rank of every score, then sends the score and document identifier to the position indexed by its rank. The first Nret values are then read out.
5On the CM-2 this routine takes time 30004r.
For example:
The algorithm is as follows:
This has the skeleton:
Its timing characteristics are:
Substituting the VP ratio r =
The system-supplied ranking function does much more work than is really required: it ranks all Ndocs scores, rather than the Nret which are ultimately used. Since we usually have Nret << Ndocs, we may look for an algorithm that avoids this unnecessary work. The algorithm that follows, called iterative extraction, accomplishes this by use of the global-maximum (>?=P) operation.
The insight is as follows: if we were only interested in the higest-ranking document, we could determine it by direct application of the global maximum operation. Having done this, we could remove that document from further consideration and repeat the operation. For example, we might start with:
We find that the largest score is 98, located at position 1. That score can be eliminated from further consideration by setting it to - 1:
On the next iteration, 83 will be the highest-ranking score. The algorithm is as follows:
This has the skeleton:
And the timing:
Substituting the VP ratio
The following algorithm, due to Jim Hutchinson (1988), improves on iterative extraction. Hutchinson's algorithm starts with an array of
scores stored in each position, at a VP ratio of 1. For example, with 32 documents, 8 processors, and 4 rows we might have the following data:
We start by extracting the largest score in each row, placing the results in a parallel variable called P_best:
We then extract the best of the best (in this case 98):
and replenish it from the appropriate row (3 in this case).
This is repeated Nret times. The algorithm involves two pieces. First is the basic extraction step:
This has the skeleton:
We do not have a separate timing figure for [S] P = [S] P, but we note that this could be rewritten as S = [S]P; [S]P = S. The timing is thus as follows:
Given this extraction step subroutine, one can easily implement Hutchinson's algorithm:
This has the skeleton:
Its timing is as follows:
Substituting in the value of Nrows we arrive at:
We have examined three ranking algorithms in this section: the system-defined ranking algorithm, iterative extraction, and Hutchinson's algorithm. Their times are as follows:
For very small versions of Nret, iterative extraction is prefered; for very large values of Nret, the system ranking function is preferred, but in most cases Hutchinson's algorithm will be preferred. Considering various sizes of database, with a 65,536 processor Connection Machine, and our standard database parameters, the following rank times should be observed:
The time required to rank documents is clearly not an obstacle to the implementation of very large IR systems. The remainder of the chapter will be concerned with several methods for representing and scoring documents; these methods will then use one of the algorithms described above (presumably Hutchinson's) for ranking.
The first scoring method to be considered here is based on parallel signature files. This file structure has been described by Stanfill and Kahle (1986, 1988, 1990a) and by Pogue and Willet (1987). This method is an adaptation of the overlap encoding techniques discussed in this book.
Overlap encoded signatures are a data structure that may be quickly probed for the presence of a word. A difficulty associated with this data structure is that the probe will sometimes return present when it should not. This is variously referred to as a false hit or a false drop. Adjusting the encoding parameters can reduce, but never eliminate, this possibility. Depending on the probability of such a false hit, signatures may be used in two manners. First, it is possible to use signatures as a filtering mechanism, requiring a two-phase search in which phase 1 probes a signature file for possible matches and phase 2 re-evaluates the query against the full text of documents accepted by phase 1. Second, if the false hit rate is sufficiently low, it is possible to use signatures in a single phase system. We will choose our signature parameters in anticipation of the second case but, if the former is desired, the results shown below may still be applied.
An overlap encoding scheme is defined by the following parameters:
Unless otherwise specified, the following values will be used:
A signature is created by allocating Sbits bits of memory and initializing them to 0. To insert a word into a signature, each of the hash functions is applied to the word and the corresponding bits set in the signature. The algorithm for doing this is as follows:
The timing characteristics of this algorithm will not be presented.
To test a signature for the presence of a word, all Sweight hash functions are applied to it and the corresponding bits of the signature are ANDed together. A result of 0 is interpreted as absent and a result of 1 is interpreted as present.
This has the skeleton:
Its timing is:
The VP ratio will be determined by total number of signatures in the database. This, in turn, depends on the number of signatures per document. A randomly chosen document will have the length L, and require
signatures. If the distribution of L is reasonably smooth, then a good approximation for the average number of signatures per document is:
The number of signatures in a database is then
and the VP ratio is
We can now compute the average time per query term:
Documents having more than Swords must be split into multiple signatures. These signatures can then be placed in consecutive positions, and flag bits used to indicate the first and last positions for each document. For example, given the following set of documents:
we might arrive at signatures divided as follows:
We can then determine which documents contain a given word by (1) probing the signatures for that word, and (2) using a scan_with_or opcration to combine the results across multiple positions. For example, probing for "yet" we obtain the following results:
This routine returns either 1 or 0 in the last position of each document, according to whether any of its signatures contained the word. The value at other positions is not meaningful.
The algorithm for this is as follows:
This is the skeleton:
Its timing is:
Using the above building blocks, it is fairly simple to construct a scoring alogrithm. In this algorithm a query consists of an array of terms. Each term consists of a word and a weight. The score for a document is the sum of the weights of the words it contains. It may be implemented thus:
This has the skeleton:
Its timing characteristics are as follows:
It is straightforward to implement Boolean queries with the probe_document operation outlined above. Times for Boolean queries will be slightly less than times for document scoring. As a simplification, each query term may be: (1) a binary AND operation, (2) a binary OR operation, (3) a NOT operation, or (4) a word. Here is a complete Boolean query engine:
The timing characteristics of this routine will not be considered in detail; it should suffice to state that one call to probe_document is required for each word in the query, and that probe_document accounts for essentially all the time consumed by this routine.
The bulk of the time in the signature scoring algorithm is taken up by the probe_document operation. The bulk of the time for that operation, in turn, is taken up by the scan_with_or operation. This operation is performed once per query term. We should then seek to pull the operation outside the query-term loop. This may be done by (1) computing the score for each signature independently, then (2) summing the scores at the end. This is accomlished by the following routine:
This has the skeleton:
The timing characteristics are as follows:
Comparing the two scoring algorithms, we see:
The dominant term in the timing formula, Ntermsr, has been reduced from 119 to 63 so, in the limit, the new algorithm is 1.9 times faster. The question arises, however, as to what this second algorithm is computing. If each query term occurs no more than once per document, then the two algorithms compute the same result. If, however, a query term occurs in more than one signature per document, it will be counted double or even treble, and the score of that document will, as a consequence, be elevated. This might, in fact, be beneficial in that it yields an approximation to document-term weighting. Properly controlled, then, this feature of the algorithm might be beneficial. In any event, it is a simple matter to delete duplicate word occurances before creating the signatures.
The final step in executing a query is to rank the documents using one of the algorithms noted in the previous section. Those algorithms assumed, however, that every position contained a document score. The signature algorithm leaves us with only the last position of each document containing a score. Use of the previously explained algorithms thus requires some slight adaptation. The simplest such adaptation is to pad the scores out with - 1. In addition, if Hutchinson's ranking algorithm is to be used, it will be necessary to force the system to view a parallel score variable at a high VP ratio as an array of scores at a VP ratio of 1; the details are beyond the scope of this discussion.
Taking into account the VP ratio used in signature scoring, the ranking time will be:
Substituting the standard values for Nterms, Nret,
and a ranking time of:
The times for various sizes of database, on a machine with 65,536 processors, are as follows:
It is possible that a signature file will not fit in primary storage, either because it is not possible to configure a machine with sufficient memory or because the expense of doing so is unjustified. In such cases it is necessary that the signature file reside on either secondary or tertiary storage. Such a file can then be searched by repetitively (1) transferring signatures from secondary storage to memory, (2) using the above signature-based algorithms to score the documents, and (3) storing the scores in a parallel array. When the full database has been passed through memory, any of the above ranking algorithms may be invoked to find the best matches. The algorithms described above need to be modified, but the compute time should be unchanged. There will, however, be the added expense of reading the signature file into primary memory. If RIO is the I/O rate in megabytes per second, and c is the signature file compression factor (q.v. below), then the time to read a signature file through memory will be:
Comparing the I/O time with the compute time, it is clear that this method is I/O bound. As a result, it is necessary to execute multiple queries in one batch in order ot make good use of the compute hardware. This is done by repeatedly (1) transferring signatures from secondary storage to memory: (2) calling the signature- based scoring routine once for each query; and (3) saving the scores produced for each query in a separate array. When all signatures have been read, the ranking algorithm is called once for each query. Again, the algorithms described above need modification, but the basic principles remain unchanged. Given the above parameters, executing batches of 100 queries seems reasonable, yielding the following times:
This has not, in practice, proved an attractive search method.
It is guaranteed that, if a word is inserted into a signature, probing for it will return present. It is possible, however, for a probe to return present for a word that was never inserted. This is referred to variously as a false drop or a false hit. The probability of a false hit depends on the size of the signature, the number of hash codes, and the number of bits set in the table. The number of bits actually set depends, in turn, on the number of words inserted into the table. The following approximation has proved useful:
There is a trade-off between the false hit probability and the amount of space required for the signatures. As more words are put into each signature (i.e., as Swords increases), the total number of signatures decreases while the probability of a false hit increases. We will now evaluate the effects of signature parameters on storage requirements and the number of false hits.
A megabyte of text contains, on the average, Rdocs documents, each of which requires an average of
6The compression factor is defined as the ratio of the signature file size to the full text.
If we multiply the number of signatures per megabyte by Pfalse, we get the expected number of false hits per megabyte:
We can now examine how varying Swords alters the false hit probability and the compression factor:
Signature representations may also be tuned by varying Sbits and Swords in concert. As long as Sbits = kSwords for some constant k, the false hit rate will remain approximately constant. For example, assuming Sweight = 10 and Sbits = 34.133Swords, we get the following values for Pfalse:
Since the computation required to probe a signature is constant regardless of the size of the signature, doubling the signature size will (ideally) halve the number of signatures and consequently halve the amount of computation. The degree to which computational load may be reduced by increasing signature size is limited by its effect on storage requirements. Keeping Sbits = 34.133Swords, Sweight = 10 and varying Swords, we get the following compression rates:
Clearly, for a fixed k (hence, as described above, a fixed false hit rate), storage costs increase as Sbits increases, and it is not feasible to increase Sbits indefinitely.
For the database parameters assumed above, it appears that a signature size of 4096 bits is reasonable.
The signature-based algorithms described above have a number of advantages and disadvantages. There are two main disadvantages. First, as noted by Salton and Buckley (1988) and by Croft (1988), signatures do not support general document-term weighting, a problem that may produce results inferior to those available with full document-term weighting and normalization. Second, as pointed out by Stone (1987), the I/O time will, for single queries, overwhelm the query time. This limits the practical use of parallel signature files to relatively small databases which fit in memory. Parallel signature files do, however, have several strengths that make them worthy of consideration for some applications. First, constructing and updating a signature file is both fast and simple: to add a document, we simply generate new signatures and append them to the file. This makes them attractive for databases which are frequently modified. Second, the signature algorithms described above make very simple demands on the hardware; all local operations can be easily and efficiently implemented using bit-serial SIMD hardware, and the only nonlocal operation scan_with_add can be efficiently implemented with very simple interprocessor communication methods which scale to very large numbers of processors. Third, signature representations work well with serial storage media such as tape. Given recent progress in the development of high-capacity, high-transfer rate, low-cost tape media, this ability to efficiently utilize serial media may become quite important. In any event, as the cost of random access memory continues to fall, the restriction that the database fit in primary memory may become less important.
An inverted file is a data structure that, for every word in the source file, contains a list of the documents in which it occurs. For example, the following source file:
has the following inverted index:
Each element of an inverted index is called a posting, and minimally consists of a document identifier. Postings may contain additional information needed to support the search method being implemented. For example, if document-term weighting is used, each posting must contain a weight. In the event that a term occurs multiple times in a document, the implementer must decided whether to generate a single posting or multiple postings. For IR schemes based on document-term weighting, the former is preferred; for schemes based on proximity operations, the latter is most useful.
The two inverted file algorithms described in this chapter differ in (1) how they store and represent postings, and (2) how they process postings.
The parallel inverted file structure proposed by Stanfill, Thau, and Waltz (1989) is a straightforward adaptation of the conventional serial inverted file structure. A parallel inverted file is a parallel array of postings such that the postings for a given word occupy contiguous positions within a contiguous series of rows, plus an index structure indicating the start row, end row, start position, and end position of the block of postings for each word. For example, given the database and inverted file shown above, the following parallel inverted file would result:
In order to estimate the performance of algorithms using this representation, it is necessary to know how many rows of postings need to be processed. The following discussion uses these symbols:
Assume the first posting for term Ti is stored starting at (r, p). The last posting for Ti will then be stored at
and the number of rows occupied by Ti will be
Assuming p is uniformly distributed between 0 and Nprocs-1, the expected value of this expression is
From our frequency distribution model we know Ti occurs f (Ti) times per megabyte, so Pi = |D| f (Ti). This gives us:
Taking into account the random selection of query terms (the random variable Q), we get a formula for the average number of rows per query-term:
Also from the distribution model, f(Q) = Z, and
The scoring algorithm for parallel inverted files involves using both left- and right-indexing to increment a score accumulator. We start by creating an array of score registers, such as is used by Hutchinson's ranking algorithm. Each document is assigned a row and a position within that row. For example, document i might be mapped to row i mod Nprocs, position
The inner loop of this algorithm will be executed, on the average,
This has the following timing characteristics:
Taking into account the value of
Substituting our standard value for
Up to now, the algorithms we have discussed support only binary document models, in which the only information encoded in the database is whether a given term appears in a document or not. The parallel inverted file structure can also support document term weighting, in which each posting incorporates a weighting factor; this weighting factor measures the strength of usage of a term within the document. The following variant on the query execution algorithm is then used:
This algorithm requires only slightly more time than the unweighted version.
18.7 PARTITIONED POSTING FILES
One major advantage of inverted files is that it is possible to query them without loading the entire file into memory. The algorithms shown above have assumed that the section of the file required to process a given query are already in memory. While a full discussion of the evolving field of I/O systems for parallel computing is beyond the scope of this paper, a brief presentation is in order. In the final analysis, most of what is known about I/O systems with large numbers of disks (e.g. mainframe computers) will probably hold true for parallel systems.
This discussion is oriented towards the partitioned posting file representation. For this algorithm, the disk system is called on to simply read partitions into memory.
I/O systems for parallel computers are typically built from large arrays of simple disks. For example, the CM-2 supports a disk array called the Data VaultTM which contains 32 data disk plus 8 ECC disks.8 It may be thought of as a single disk drive with an average latency of 200 milliseconds and a transfer rate of 25 MB/sec- ond. Up to 8 Data Vaults may be simultaneously active, yielding a transfer rate of up to 200 MB/second. This access method achieves very high transfer rates, but does not yield many I/O's per second; this can be crippling for all but the very largest databases. Consider, for example, a 64K processor Connection Machine with 8 disk arrays operating in single transfer mode. Assume we are using the partitioned posting file representation, and that each posting requires 4 bytes of storage. The storage required by each partition is then 4FNprocs.
8Data Vault is a trademark of Thinking Machines Corporation
The average query-term requires NP partitions to be loaded. These partitions may be contiguously stored on disk, so the entire group of partitions may be transferred in a single operation. The time is then:
Given a seek time of 200 milliseconds and a transfer rate of 200 M-B/second, plus our other standard assumptions, the following per-term times will result:
Under these circumstances, the system is severely seek-bound for all but the very largest databases.
Fortunately, the disk arrays contain buried in them the possibility of solving the problem. Each Data Vault has 32 disks embedded in it; a system with 8 disk arrays thus has a total of 256 disks. It is possible to access these disks independently. Under this I/O model, each disk transfers a block of data into the memories of all processors. The latency is stil 200 milliseconds, but 256 blocks of data will be transferred rather than l. This has the capability of greatly reducing the impact of seek times on system performance.
At this point in time, independent disk access methods for parallel computers are still in development; considerable work is required to determine their likely performance in the context of information retrieval. Stanfill and Thau (1991) have arrived at some preliminary results.
The basic algorithmic issues associated with implementing information retrieval systems on databases of up to 1000 GB may be considered solved at this point in time.
The largest difficulty remaining in the implementation of parallel inverted file algorithms remains the I/O system. Disk arrays, operating in single-transfer mode, do not provide a sufficiently large number of I/O's per second to match available processing speeds until database sizes approach a thousand Gigabytes or more. Multi-transfer I/O systems have the potential to solve this problem, but are not yet available for data parallel computers. At this point, parallel inverted file algorithms are restricted to databases which either fit in primary memory or are large enough that the high latency time is less of an issue. However, these problems are very likely to find solution in the next few years.
It should be clear at this point that the engineering and algorithmic issues involved in building large-scale Information Retrieval systems are well on their way to solution and, over the next decade, we can reasonably look forward to interactive access to text databases, no matter how large they may be.
CROFT, B. (1988). Implementing Ranking Strategies Using Text Signatures. ACM Transactions on Office Information Systems, 6(1), 42-62.
HILLIS, D. (1985) The Connection Machine, Cambridge, MA: MIT Press.
HILLIS, D. & and STEELE, G. (1986). Data Parallel Algorithms. Communications of the ACM, 29(12), 1170-1183.
HUTCHINSON, J. (1988). Personal Communications.
POGUE, C. & WILLETT, P. (1987). Use of Text Signatures for Document Retrieval in a Highly Parallel Environment. Parallel Computing, 4, 259-268.
SALTON, G. & BUCKLEY, C. (1988). Parallel Text Search Methods. Communications of the ACM, 31(2), 202-215.
STANFILL, C. & KAHLE, B. (1986). Parallel Free-Text Search on the Connection Machine System. Communications of the ACM, 29 (12), 1229-1239.
STANFILL, C. (1988a). Parallel Computing for Information Retrieval: Recent Developments. Technical Report DR88-1. Cambridge, MA: Thinking Machines Corporationl
STANFILL, C., THAU, R. & WALTZ, D. (1989). A Parallel Indexed Algorithm for Information Retrieval. Paper Presented at the International Conference on Research and Development in Information Retrieval. Cambridge, MA.
STANFILL, C. (1990a). Information Retrieval Using Parallel Signature Files. IEEE Data Engineering Bulletin, 13 (1), 33-40.
STANFILL, C. (1990b). Partitioned Posting Files: a Parallel Inverted File Structure for Information Retrieval. Paper presented at the International Conference on Research and Development in Information Retrieval. Brussels, Belgium.
STANFILL, C. & THAU, R. (1991). Information Retrieval on the Connection Machine: 1 to 8192 Gigabytes. Information Processing and Management, 27(4), 285-310.
STONE, H. (1987). Parallel Querying of Large Databases: a Case Study. Computer, 20(10), 11-21.
Thinking Machines Corporation. (1987). Connection Machine model CM-2 technical specifications. Cambridge, MA: Thinking Machines Corporation.
Thinking Machines Corporation. (1990). C* Programming Guide. Cambridge, MA: Thinking Machines Corporation.
18.1 INTRODUCTION
. 1 Second, we will define a model of the retrieval task that will allow us to derive performance estimates. Third, we will look at algorithms for ranking documents once they have been scored.2 Fourth, we will consider one database representation, called parallel signature files, which represents the database as a set of signatures. Fifth, we will consider two different file structures based on inverted indexes. Sixth, we will briefly look at issues relating to secondary storage and I/O. Finally, we will summarize the results and delineate areas for continued research., CM, and DataVault are trademarks of Thinking Machines Corporation.18.2 DATA PARALLEL COMPUTING
18.2.1 Shapes and Local Computation
P_1 8 6 3 4 9 1 2 0
-------------------------------
P_2 7 14 8 29 17 34 1 9
P_array [0] 4 38 17 87 30 38 90 81
-------------------------------------------
P_array [1] 37 3 56 39 89 10 10 38
-------------------------------------------
P_array [2] 01 83 79 85 13 87 38 61
P_z = P_x * P_y;
P_x 1 1 1 2 2 2 3 3
P_y 1 2 3 1 2 3 1 2
---------------------------
P_z 1 2 3 2 4 6 3 6
where (P_1 P_2)
P_min = P_1;
else
P_min = P_2;
18.2.2 Nonlocal Operations
+= Cumulative sum
&= Cumulative bitwise AND
|= Cumulative bitwise OR
>?= Cumulative maximum
<?= Cumulative minimum
P_x 5 0 6 4 1 7 3 2
P_i 7 4 1 2 5 0 6 3
---------------------------
P_y 7 6 4 2 0 1 3 5
= Send with overwrite (arbitrary choice)
+= Send with add
&= Send with bitwise AND
= Send with bitwise OR <?= Send with minimum
>?= Send with maximum
P_x 2 0 1 2 4 3 2 1
scan_with_add (P_x) 2 2 3 5 9 12 14 15
P_x 2 0 1 2 4 3 2 1
B_s 1 0 0 0 1 0 1 0
add_scan (P_x, B_s) 2 2 3 5 4 7 2 3
18.2.3 Performance Model
Nprocs The number of physical processors
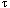The VP ratiosum_array(P_array)
{P_result = 0;
for (i = 0; i< N; i++)
P_result += P_array;
return (+= P_result);
}
P = S
loop (N)
P += P
(+= P)
Operation Calls Time per Call
------------------------------------------
P = S 1 3 + 15r
P += P n 3 + 28r
(+= P) 1 137 + 70r
------------------------------------------
Total (140 + 3n) + (85 + 28n)r
Operator Time r = 1 Comments
B = S 3 + 3r 6
B $= B 3 + 3r 6
B $$ B 3 + 3r 6
where(B) 8 + 2r 10
S = [S]P 16 16
[S]P = S 16 16
P = S 3 + 15r 18
P += S 3 + 28r 31
P += P 3 + 28r 31
P[P] = P 11 + 60r 71
P = P[P] 11 + 60r 71
P == S 18 + 67r 85 Same time for <= etc.
(>?= P) 137 + 70r 207 Same time for += etc.
scan_with_or 632 + 56r 688
scan_with_add 740 + 170r 910
[P]P = P 2159r 2159 Same time for += etc.
[P]P[P] = P 2159r 2159 Same time for += etc.
18.4 RANKING
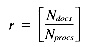
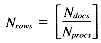
18.4.1 System-Supplied Rank Functions
P_score 83 98 1 38 78 37 17 55
------------------------------------------
rank 1 0 7 4 2 5 6 3
After send 98 83 78 55 38 37 17 1
rank_system(dest, P_doc_score, P_doc_id)
{P_rank = rank(P_doc_score);
[P_rank]P_doc_score = P_doc_score;
[P_rank] P_doc_id = P_doc_id;
for (i = 0; i < N_RET; i++)
{dest[i].score = [i] P_doc_score;
dest[i].id = [i]P_doc_id;
}
}
P = rank ()
[P]P = P
[P]P = P
loop (N_RET)
{S = [S]P
S = [S]P
}
Operation Calls Time per Call
-----------------------------------
rank ( ) 1 30004r
P]P = P 2 2159r
S = [S]P 2Nret 16
-----------------------------------
Total 32Nret + 34322r
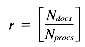gives a time of: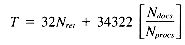
18.4.2 Iterative Extraction
P_score 83 98 1 38 78 37 17 55
P_score 83 -1 1 38 78 37 17 55
rank_iterative(dest, P_doc_score, P_doc_id)
{for (i = 0; i < N_RET; i++)
{best_score = ( > ?= P_doc_score);
where (P_doc_score == best_score)
{position = ( <?= P_position);
dest[i].score = [position]P_doc_score;
dest[i].id = [position]P_doc_id;
[position]P_doc_score = -1;
}
}
}
loop (N_RET)
{S = ( >?= P)
where (P == S)
{S = ( <?= P)
S = [S]P
S = [S]P
[S]P = S
}
}
Operation Calls Time per Call
------------------------------------
(>? = P) 2Nret 137 + 70r
P == S Nret 18 + 67r
where Nret 8 + 2r
S = [S]P 2Nret 16
[S]P = S Nret 16
------------------------------------
Total 348Nret + 209Nretr
gives a time of:
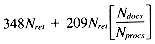
18.4.3 Hutchinson's Algorithm
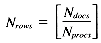
P_scores [0] 88 16 87 10 94 04 21 11
P_scores [1] 90 17 83 30 37 39 42 17
P_scores [2] 48 43 10 62 4 12 10 9
P_scores [3] 83 98 1 38 78 37 17 55
P_scores [0] 88 16 87 10 -1 4 21 11
P_scores [1] -1 17 83 30 37 39 42 17
P_scores [2] 48 43 10 -1 4 12 10 9
P_scores [3] 83 -1 1 38 78 37 17 55
--------------------------------------------
P_best 94 90 62 98 -1 -1 -1 -1
P_scores [0] 88 16 87 10 94 4 21 11
P_scores [1] -1 17 83 30 37 39 42 17
P_scores [2] 48 43 10 -1 4 12 10 9
P_scores [3] 83 -1 1 38 78 37 17 55
--------------------------------------------
P_best 94 90 62 -1 -1 -1 -1 -1
P_scores [0] 88 16 87 10 94 4 21 11
P_scores [1] -1 17 83 30 37 39 42 17
P_scores [2] 48 43 10 -1 4 12 10 9
P_scores [3] -1 -1 1 38 78 37 17 55
--------------------------------------------
P_best 94 90 62 83 -1 -1 -1 -1
extract_step(P_best_score, P_best_id, P_scores, P_ids, row)
{max_ score = (>?= P_ scores[row]);
where (P_ scores[row] == max_score)
{position = (<?= P_position);
[row]P_best_score = [position]P_scores[row];
[row]P_best_id = [position]P_scores[row];
[position]P_scores[row] = -1;
}
}
S = (>?= P)
where(P == S)
{S = (<?= P)
[S] P = [S] P
[S] P = [S] P
[S] P = S
}
Operation Calls Time per Call
-------------------------------
(>?= P) 2 207
where l 10
S == P 1 85
[S]P = S 3 16
S = [S] P 2 16
-------------------------------
Total 589
rank_hutchinson(dest, P_scores, P_ids)
{P_best_score = -1;
P_best_id = 0;
for (row = 0; row < N_ROWS; row++)
extract_step(P_best_score, P_best_id,
P_scores, P_ids, row);
for (i = 0; i < N_RET; i++)
{best_of_best = (>?= P_best_score);
where (P_best_score == best_of_best)
{position = (<?= P_position);
dest [i].score = [position]P_scores;
dest[i].id = [position]P_ids;
[positions]P_best_score = -1;
}
extract_step(P_best_score, P_best_id,
P_scores, P_ids, row);
}
}
P = S
P = S
loop(N_ROWS)
extract_step ()
loop(N_RET)
{S = (>?= P)
where(P == S)
{S = (<?= P)
S = [S]P
S = [S]P
[S]P = S
}
extract_step()
}
Operation Calls Time per Call
-------------------------------------------------
( > ? = P ) 2Nret 207
S == P Nret 85
whereV Nret 10
S= [S]P 2Nret 16
[S]P = S Nret 16
extract_step (Nrows + Nret) 589
-------------------------------------------------
Total 1149Nret + 589Nrows
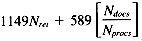
18.4.4 Summary
|D| Ndocs System Iterative Hutchinson
1 GB 200 X 103 138 ms 24 ms 25ms
10 GB 2 X 106 1064 ms 137 ms 41 ms
100 GB 20 X 106 10503 ms 1286 ms 203 ms
1000 GB 200 X 106 104751 ms 12764 ms 1821 ms
18.5 PARALLEL SIGNATURE FILES
18.5.1 Overlap Encoding
Sbits Size of signature in bits
Sweight Weight of word signatures
Swords Number of words to be inserted in each signature
Hj(Ti) A set of Sweight hash functions
Sbits 4096
Sweight 10
Swords 120
create_signature (B_signature, words)
{for (i = 0; i < S_BITS; i++)
B_signature[i] = 0;
for (i = 0; i < S_WORDS; i++)
for (j = 0; j < S_WEIGHT; j++)
B_signature[hash(j, words[i])] = 1;
}
18.5.2 Probing a Signature
probe_signature(B_signature, word)
{B_result = 1;
for (i = 0; i < S_WEIGHT; i++)
B_result &= B_signature[i];
return B-result;
}
B = S
loop(S_WEIGHT)
B &= B
Operation Calls Time per Call
-----------------------------------------------------
B = S 1 3 + 3r
B &= B Sweight 3 + 3r
-----------------------------------------------------
Total 3(1 + Sweight)(1 + r)
Total for Sweight = 10 33 + 33r
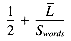
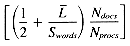
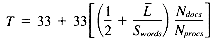
18.5.3 Scoring Algorithms
______________________________________________________________
| | | Still another |
| This is the initial | This is yet another | document taking |
| document | document | yet more space |
| | | than the others |
|_____________________|_____________________|__________________|
Still
This initial This another another taking space
is the docu- is yet docu- docu- yet than others
B_signature ment ment ment more the
-----------------------------------------------------------------------------
B_first 1 0 1 0 1 0 0 0
B_last 0 1 0 1 0 0 0 1
Still
This initial This another another taking space
is the docu- is yet docu- docu- yet than others
B_signature ment ment ment more the
------------------------------------------------------------------------------
B_first 1 0 1 0 1 0 0 0
B_last 0 1 0 1 0 0 0 1
probe
("yet") 0 0 1 0 0 1 0 0scan_with_or 0 0 1 1 0 1 1 1
probe_document(B_signature, B_first, word)
{B_local = probe_signature(B_signature, word);
B_result = scan_with_or(B_local, B_first);
}
B = probe_signature()
B = scan_with_or()
Operation Calls Time per Call
-------------------------------------
probe_signature 1 33 + 33r
scan_with_or 1 632 + 56r
-------------------------------------
Total 665 + 89r
score_document(B_signature, B_first, terms)
{P_score = 0;
for (i = 0; i < N_TERMS; i++)
{B_probe = probe_document(B_signature, terms[i].word, B_first)
where (B_probe)
P_score += terms[i].weight;
}
return P_score;
}
P = S
loop (N_TERMS)
{B = probe_document()
where(B)
P += S
}
Operation Calls Time per Call
-------------------------------------------------------
P = S 1 3 + 15r
probe_document Nterms 665 + 89r
where Nterms 8 + 2r
P += S Nterms 3 + 28r
-------------------------------------------------------
Total 3 + 676Nterms + (15 + 119Nterms)r
query(B_signature, B_first, term)
{arg0 = term-args[0];
arg1 = term-args[1];
switch (term-connective)
{case AND: return query(B_signature, B_first, arg0) &&
query(B_signature, B_first, arg1);
case OR: return query(B_signature, B_first, arg0)
query(B_signature, B_first, arg1);
case NOT: return ! query(B_signature, B_first, arg0);
case WORD: return probe_document(B_signature, B_first, arg0);
}
}
18.5.4 An Optimization
score_document(B_signature, B_first, terms)
{P_score = 0;
for (i = 0; i < N_TERMS; i++)
{B_probe = probe_signature(B_signature, term[i].word);
where (B_probe)
P_score += term[i].weight;
}
P_score = scan_with_add(P_score, B_first);
return P_score;
}
P = S;
loop (N_TERMS)
{B = probe_signature ();
where (B)
P += S;
}
P = scan_with_add ();
Operation Calls Time per Call
-----------------------------------------------------------
P = S 1 3 + 15r
probe_signature Nterms 33 + 33r
where Nterms 8 + 2r
P += S Nterms 3 + 28r
scan_with_add 1 740 + 170r
-----------------------------------------------------------
Total (743 + 44Nterms) + (185 + 63Nterms)r
Basic Algorithm (3 + 676Nterms) + (15 + 119Nterms)r
Improved Algorithm (743 + 44Nterms) + (185 + 63Nterms)r
18.5.5 Combining Scoring and Ranking
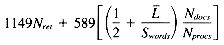
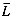, and Swords gives us a scoring time of: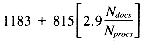
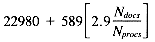
D Ndocs Score Rank Total 1 GB 200 X 103 9 ms 28 ms 37 ms
10 GB 2 X 106 74 ms 75 ms 149 ms
100 GB 20 X 106 723 ms 545 ms 1268 ms
1000 GB 200 X 106 7215 ms 5236 ms 12451 ms
18.5.6 Extension to Secondary/Tertiary Storage
For a fully configured CM-2, RIO = 200. The signature parameters we have assumed yield a compression factor c = 30 percent (q.v. below). This leads to the following I/O times:
D I/O Time 1 GB 2 sec
10 GB 15 sec
100 GB 150 sec
1000 GB 1500 sec
Search Time
D I/O Time (100 queries) Total 1 GB 2 sec 4 sec 6 sec
10 GB 15 sec 15 sec 30 sec
100 GB 150 sec 127 sec 277 sec
100 GB 1500 sec 1245 sec 2745 sec
18.5.7 Effects of Signature Parameters
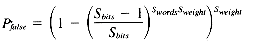
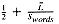signatures. Each signature, in turn, requires 
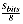bytes of storage. Multiplying the two quantities yields the number of bytes of signature space required to represent 1 megabyte of input text. This gives us a compression factor6 of: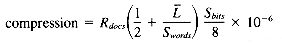
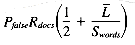
Swords Signatures/MB Compression Pfalse False hits/GB
40 1540 77% 4.87 X 10-11 7.50 X 10-5
80 820 42% 3.09 X 10-8 2.50 X 10-2
120 580 30% 1.12 X 10-6 6.48 X 10-1
160 460 24% 1.25 X 10-5 5.75 X 100
200 388 20% 7.41 X 10-5 2.88 X 101
240 340 17% 2.94 X 10-4 1.00 X 102
280 306 16% 8.88 X 10-4 2.72 X 102
320 280 14% 2.20 X 10-3 6.15 X 102
Swords Sbits Pfalse
80 2731 1.1163 X 10-6
120 4096 1.1169 X 10-6
160 5461 1.1172 X 10-6
Swords Sbits c
60 2048 27%
120 4096 30%
240 8192 35%
18.5.8 Discussion
18.6 PARALLEL INVERTED FILES
______________________________________________________________
| | | Still another |
| This is the initial | This is yet another | document taking |
| document | document | yet more space |
| | | than the others |
|_____________________|_____________________|__________________|
another 1 2
document 0 1 2
initial 0
is 0 1
more 2
others 2
space 2
still 2
taking 2
than 2
the 0 2
this 0 1
yet 1 2
18.6.1 Data Structure
Postings
----------
1 2 0 1
2 0 0 1
2 2 2 2
2 2 0 2
0 1 1 2
Index
-----------------------------------------
Word First First Last Last
Row Position Row Position
-----------------------------------------
another 0 0 0 1
document 0 2 1 0
initial 1 1 1 1
is 1 2 1 3
more 2 0 2 0
others 2 1 2 1
space 2 2 2 2
still 2 3 2 3
taking 3 0 3 0
than 3 1 3 1
the 3 2 3 3
this 4 0 4 1
yet 4 2 4 3
Pi The number of postings for term Ti
Ri The number of rows in which postings for Ti occur
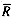The average number of rows per query term(r, p) A row-position pair
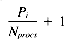
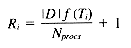
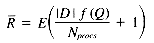
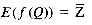. This gives us: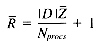
18.6.2 The Scoring Algorithm
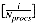. Each posting is then modified so that, rather than containing a document identifier, it contains the row and position to which it will be sent. The Send with add operation is then used to add a weight to the score accumulator. The algorithm is as follows:score_term (P_scores, P_postings, term)
{for (row = term.start_row; row <= term.end_row; row++)
{if (row == term.start_row)
start_position = term.start_position;
else
start_position = 0;
if (row == term.end_row)
end_position = term.end_position;
else
end_position = N_PROCS-1;
where ((start_position <= P_position) &&
(P_position <= end_position))
{P_dest_pos = P_postings[row].dest_pos;
P_dest_row = P_postings[row].dest_row;
[P_dest_pos] P_scores [P_dest_row] += term.weight;
}
}
}
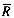times. This yields the following skeleton:loop(R_BAR)
where ((S = P) && (P = S)) /* Also 1 B && B operation */
[P] P [P] += S
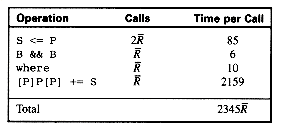
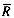yields the following time per query term: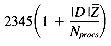
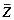, we get times for a 65,536 processor CM-2. Times for scoring 10 terms and for ranking are also included. Finally, the total retrieval time for a 10-term query is shown |D| Time 10 Terms Rank Total
1 GB 2 ms 25 ms 25 ms 50 ms
10 GB 3 ms 34 ms 41 ms 75 ms
100 GB 13 ms 131 ms 203 ms 334 ms
1000 GB 110 ms 1097 ms 1821 ms 2918 ms
18.6.3 Document Term Weighting
score_weighted_term (P_scores, P_postings, term)
{for (row = term.start_row; row = term.end_row; row++)
{if (row == term.start_row)
start_position = term.start_position;
else
start_position = 0;
if (row == term.end_row)
end_position = term.end_position;
else
end_position = N_PROCS-1;
where ((start_position = P_position) &&
(P_position = end_position))
{P_dest_pos = P_postings[row].dest_pos;
P_dest_row = P_postings[row].dest_row;
P_weight = term.weight * P_postings[row].weight;
[P_dest_pos] P_scores [P_dest_row] += P_weight;
}
}
}
18.8 SECONDARY STORAGE
18.8.1 Single-Transfer I/O on Disk Arrays
D Seek Transfer Score 1 GB 200 ms 5 ms 1 ms
10 GB 200 ms 5 ms 1 ms
100 GB 200 ms 11 ms 2 ms
1000 GB 200 ms 65 ms 9 ms
18.8.2 Independent Disk Access
18.9 SUMMARY
REFERENCES