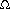 (n lg n) time.
(n lg n) time.


We have now introduced several algorithms that can sort n numbers in O(n lg n) time. Merge sort and heapsort achieve this upper bound in the worst case; quicksort achieves it on average. Moreover, for each of these algorithms, we can produce a sequence of n input numbers that causes the algorithm to run in 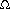 (n lg n) time.
(n lg n) time.
These algorithms share an interesting property: the sorted order they determine is based only on comparisons between the input elements. We call such sorting algorithms comparison sorts. All the sorting algorithms introduced thus far are comparison sorts.
In Section 9.1, we shall prove that any comparison sort must make
Sections 9.2 and 9.3 examine three sorting algorithms--counting sort, radix sort, and bucket sort--that run in linear time. Needless to say, these algorithms use operations other than comparisons to determine the sorted order. Consequently, the
In a comparison sort, we use only comparisons between elements to gain order information about an input sequence
In this section, we assume without loss of generality that all of the input elements are distinct. Given this assumption, comparisons of the form ai = aj are useless, so we can assume that no comparisons of this form are made. We also note that the comparisons ai
Comparison sorts can be viewed abstractly in terms of decision trees. A decision tree represents the comparisons performed by a sorting algorithm when it operates on an input of a given size. Control, data movement, and all other aspects of the algorithm are ignored. Figure 9.1 shows the decision tree corresponding to the insertion sort algorithm from Section 1.1 operating on an input sequence of three elements.
In a decision tree, each internal node is annotated by ai : aj for some i and j in the range 1
The length of the longest path from the root of a decision tree to any of its leaves represents the worst-case number of comparisons the sorting algorithm performs. Consequently, the worst-case number of comparisons for a comparison sort corresponds to the height of its decision tree. A lower bound on the heights of decision trees is therefore a lower bound on the running time of any comparison sort algorithm. The following theorem establishes such a lower bound.
Theorem 9.1
Any decision tree that sorts n elements has height
Proof Consider a decision tree of height h that sorts n elements. Since there are n! permutations of n elements, each permutation representing a distinct sorted order, the tree must have at least n! leaves. Since a binary tree of height h has no more than 2h leaves, we have
which, by taking logarithms, implies
since the lg function is monotonically increasing. From Stirling's approximation (2.11), we have
where e = 2.71828 . . . is the base of natural logarithms; thus
Corollary 9.2
Heapsort and merge sort are asymptotically optimal comparison sorts.
Proof The O(n lg n) upper bounds on the running times for heapsort and merge sort match the
9.1-1
What is the smallest possible depth of a leaf in a decision tree for a sorting algorithm?
9.1-2
Obtain asymptotically tight bounds on lg(n!) without using Stirling's approximation. Instead, evaluate the summation
9.1-3
Show that there is no comparison sort whose running time is linear for at least half of the n! inputs of length n. What about a fraction of 1/n of the inputs of length n? What about a fraction 1/2n?
9.1-4
Professor Solomon claims that the
9.1-5
Prove that 2n - 1 comparisons are necessary in the worst case to merge two sorted lists containing n elements each.
9.1-6
You are given a sequence of n elements to sort. The input sequence consists of n/k subsequences, each containing k elements. The elements in a given subsequence are all smaller than the elements in the succeeding subsequence and larger than the elements in the preceding subsequence. Thus, all that is needed to sort the whole sequence of length n is to sort the k elements in each of the n/k subsequences. Show an
Counting sort assumes that each of the n input elements is an integer in the range 1 to k, for some integer k. When k = O(n), the sort runs in O(n) time.
The basic idea of counting sort is to determine, for each input element x, the number of elements less than x. This information can be used to place element x directly into its position in the output array. For example, if there are 17 elements less than x, then x belongs in output position 18. This scheme must be modified slightly to handle the situation in which several elements have the same value, since we don't want to put them all in the same position.
In the code for counting sort, we assume that the input is an array A[1 . . n], and thus length[A] = n. We require two other arrays: the array B[1 . . n] holds the sorted output, and the array C[1 . . k] provides temporary working storage.
Counting sort is illustrated in Figure 9.2. After the initialization in lines 1-2, we inspect each input element in lines 3-4. If the value of an input element is i, we increment C[i]. Thus, after lines 3-4, C[i] holds the number of input elements equal to i for each integer i = 1, 2, . . . , k. In lines 6-7, we determine for each i = 1, 2, . . . , k, how many input elements are less than or equal to i; this is done by keeping a running sum of the array C.
Finally, in lines 9-11, we place each element A[j] in its correct sorted position in the output array B. If all n elements are distinct, then when we first enter line 9, for each A[j], the value C[A[j]] is the correct final position of A[j] in the output array, since there are C[A[j]] elements less than or equal to A[j]. Because the elements might not be distinct, we decrement C[A[j]] each time we place a value A[j] into the B array; this causes the next input element with a value equal to A[j], if one exists, to go to the position immediately before A[j] in the output array.
How much time does counting sort require? The for loop of lines 1-2 takes time O(k), the for loop of lines 3-4 takes time O(n), the for loop of lines 6-7 takes time O(k), and the for loop of lines 9-11 takes time O(n). Thus, the overall time is O(k + n). In practice, we usually use counting sort when we have k = O(n), in which case the running time is O(n).
Counting sort beats the lower bound of
An important property of counting sort is that it is stable: numbers with the same value appear in the output array in the same order as they do in the input array. That is, ties between two numbers are broken by the rule that whichever number appears first in the input array appears first in the output array. Of course, the property of stability is important only when satellite data are carried around with the element being sorted. We shall see why stability is important in the next section.
9.2-1
Using Figure 9.2 as a model, illustrate the operation of COUNTING-SORT on the array A =
9.2-2
Prove that COUNTING-SORT is stable.
9.2-3
Suppose that the for loop in line 9 of the COUNTING-SORT procedure is rewritten:
Show that the algorithm still works properly. Is the modified algorithm stable?
9.2-4
Suppose that the output of the sorting algorithm is a data stream such as a graphics display. Modify COUNTING-SORT to produce the output in sorted order without using any substantial additional storage besides that in A and C. (Hint: Link elements of A that have the same key into lists. Where is a "free" place to keep the pointers for the linked list?)
9.2-5
Describe an algorithm that, given n integers in the range 1 to k, preprocesses its input and then answers any query about how many of the n integers fall into a range [a . . b] in O(1) time. Your algorithm should use O(n + k) preprocessing time.
Radix sort is the algorithm used by the card-sorting machines you now find only in computer museums. The cards are organized into 80 columns, and in each column a hole can be punched in one of 12 places. The sorter can be mechanically "programmed" to examine a given column of each card in a deck and distribute the card into one of 12 bins depending on which place has been punched. An operator can then gather the cards bin by bin, so that cards with the first place punched are on top of cards with the second place punched, and so on.
For decimal digits, only 10 places are used in each column. (The other two places are used for encoding nonnumeric characters.) A d-digit number would then occupy a field of d columns. Since the card sorter can look at only one column at a time, the problem of sorting n cards on a d-digit number requires a sorting algorithm.
Intuitively, one might want to sort numbers on their most significant digit, sort each of the resulting bins recursively, and then combine the decks in order. Unfortunately, since the cards in 9 of the 10 bins must be put aside to sort each of the bins, this procedure generates many intermediate piles of cards that must be kept track of. (See Exercise 9.3-5.)
Radix sort solves the problem of card sorting counterintuitively by sorting on the least significant digit first. The cards are then combined into a single deck, with the cards in the 0 bin preceding the cards in the 1 bin preceding the cards in the 2 bin, and so on. Then the entire deck is sorted again on the second least-significant digit and recombined in a like manner. The process continues until the cards have been sorted on all d digits. Remarkably, at that point the cards are fully sorted on the d-digit number. Thus, only d passes through the deck are required to sort. Figure 9.3 shows how radix sort operates on a "deck" of seven 3-digit numbers.
It is essential that the digit sorts in this algorithm be stable. The sort performed by a card sorter is stable, but the operator has to be wary about not changing the order of the cards as they come out of a bin, even though all the cards in a bin have the same digit in the chosen column.
In a typical computer, which is a sequential random-access machine, radix sort is sometimes used to sort records of information that are keyed by multiple fields. For example, we might wish to sort dates by three keys: year, month, and day. We could run a sorting algorithm with a comparison function that, given two dates, compares years, and if there is a tie, compares months, and if another tie occurs, compares days. Alternatively, we could sort the information three times with a stable sort: first on day, next on month, and finally on year.
The code for radix sort is straightforward. The following procedure assumes that each element in the n-element array A has d digits, where digit 1 is the lowest-order digit and digit d is the highest-order digit.
The correctness of radix sort follows by induction on the column being sorted (see Exercise 9.3-3). The analysis of the running time depends on the stable sort used as the intermediate sorting algorithm. When each digit is in the range 1 to k, and k is not too large, counting sort is the obvious choice. Each pass over n d-digit numbers then takes time
Some computer scientists like to think of the number of bits in a computer word as being
9.3-1
Using Figure 9.3 as a model, illustrate the operation of RADIX-SORT on the following list of English words: COW, DOG, SEA, RUG, ROW, MOB, BOX, TAB, BAR, EAR, TAR, DIG, BIG, TEA, NOW, FOX.
9.3-2
Which of the following sorting algorithms are stable: insertion sort, merge sort, heapsort, and quicksort? Give a simple scheme that makes any sorting algorithm stable. How much additional time and space does your scheme entail?
9.3-3
Use induction to prove that radix sort works. Where does your proof need the assumption that the intermediate sort is stable?
9.3-4
Show how to sort n integers in the range 1 to n2 in O(n) time.
9.3-5
In the first card-sorting algorithm in this section, exactly how many sorting passes are needed to sort d-digit decimal numbers in the worst case? How many piles of cards would an operator need to keep track of in the worst case?
Bucket sort runs in linear time on the average. Like counting sort, bucket sort is fast because it assumes something about the input. Whereas counting sort assumes that the input consists of integers in a small range, bucket sort assumes that the input is generated by a random process that distributes elements uniformly over the interval [0,1). (See Section 6.2 for a definition of uniform distribution.)
The idea of bucket sort is to divide the interval [0, 1) into n equal-sized subintervals, or buckets, and then distribute the n input numbers into the buckets. Since the inputs are uniformly distributed over [0, 1), we don't expect many numbers to fall into each bucket. To produce the output, we simply sort the numbers in each bucket and then go through the buckets in order, listing the elements in each.
Our code for bucket sort assumes that the input is an n-element array A and that each element A[i] in the array satisfies 0
Figure 9.4 shows the operation of bucket sort on an input array of 10 numbers.
To see that this algorithm works, consider two elements A[i] and A[j]. If these elements fall in the same bucket, they appear in the proper relative order in the output sequence because their bucket is sorted by insertion sort. Suppose they fall into different buckets, however. Let these buckets be B[i'] and B[j'], respectively, and assume without loss of generality that i' < j'. When the lists of B are concatenated in line 6, elements of bucket B[i'] come before elements of B[j'], and thus A[i] precedes A[j] in the output sequence. Hence, we must show that A[i]
which is a contradiction, since i' < j'. Thus, bucket sort works.
To analyze the running time, observe that all lines except line 5 take O(n) time in the worst case. The total time to examine all buckets in line 5 is O(n), and so the only interesting part of the analysis is the time taken by the insertion sorts in line 5.
To analyze the cost of the insertion sorts, let ni be the random variable denoting the number of elements placed in bucket B[i]. Since insertion sort runs in quadratic time (see Section 1.2), the expected time to sort the elements in bucket
In order to evaluate this summation, we must determine the distribution of each random variable ni. We have n elements and n buckets. The probability that a given element falls into bucket B[i] is 1/n, since each bucket is responsible for 1/n of the interval [0,1). Thus, the situation is analogous to the ball-tossing example of Section 6.6.2: we have n balls (elements) and n bins (buckets), and each ball is thrown independently with probability p = 1 /n of falling into any particular bucket. Thus, the probability that ni = k follows the binomial distribution b(k; n, p), which has mean E[ni] = np = 1 and variance Var[ni] = np(1 - p) = 1- 1/n. For any random variable X, equation (6.30) gives
Using this bound in equation (9.1), we conclude that the expected time for insertion sorting is O(n). Thus, the entire bucket sort algorithm runs in linear expected time.
9.4-1
Using Figure 9.4 as a model, illustrate the operation of BUCKET-SORT on the array A =
9.4-2
What is the worst-case running time for the bucket-sort algorithm? What simple change to the algorithm preserves its linear expected running time and makes its worst-case running time O(n lg n)?
9.4-3
We are given n points in the unit circle, pi = (xi, yi), such that
9.4-4
A probability distribution function P(x) for a random variable X is defined by P(x) = Pr{X
9-1 Average-case lower bounds on comparison sorting
In this problem, we prove an
a. Suppose that each leaf of TA is labeled with the probability that it is reached given a random input. Prove that exactly n! leaves are labeled 1/n! and that the rest are labeled 0.
b. Let D(T) denote the external path length of a tree T; that is, D(T) is the sum of the depths of all the leaves of T. Let T be a tree with k > 1 leaves, and let RT and LT be the right and left subtrées of T. Show that D(T) = D(RT) + D(LT) + k.
c. Let d(m) be the minimum value of D(T) over all trees T with m leaves. Show that d(k) = min1
d. Prove that for a given value of k, the function i lg i + (k - i) lg(k - i) is minimized at i = k/2. Conclude that d(k) =
e. Prove that D(TA) =
Now, consider a randomized comparison sort B. We can extend the decision-tree model to handle randomization by incorporating two kinds of nodes: ordinary comparison nodes and "randomization" nodes. A randomization node models a random choice of the form RANDOM( 1, r) made by algorithm B; the node has r children, each of which is equally likely to be chosen during an execution of the algorithm.
f. Show that for any randomized comparison sort B, there exists a deterministic comparison sort A that makes no more comparisons on the average than B does.
9-2 Sorting in place in linear time
a. Suppose that we have an array of n data records to sort and that the key of each record has the value 0 or 1. Give a simple, linear-time algorithm for sorting the n data records in place. Use no storage of more than constant size in addition to the storage provided by the array.
b. Can your sort from part (a) be used to radix sort n records with b-bit keys in O(bn) time? Explain how or why not.
c. Suppose that the n records have keys in the range from 1 to k. Show how to modify counting sort so that the records can be sorted in place in O(n + k) time. You may use O(k) storage outside the input array. (Hint: How would you do it for k = 3?)
The decision-tree model for studying comparison sorts was introduced by Ford and Johnson [72]. Knuth's comprehensive treatise on sorting [123] covers many variations on the sorting problem, including the information- theoretic lower bound on the complexity of sorting given here. Lower bounds for sorting using generalizations of the decision-tree model were studied comprehensively by Ben-Or [23].
Knuth credits H. H. Seward with inventing counting sort in 1954, and also with the idea of combining counting sort with radix sort. Radix sorting by the least-significant digit first appears to be a folk algorithm widely used by operators of mechanical card-sorting machines. According to Knuth, the first published reference to the method is a 1929 document by L. J. Comrie describing punched-card equipment. Bucket sorting has been in use since 1956, when the basic idea was proposed by E. J. Isaac and R. C. Singleton.
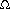 (n lg n) comparisons in the worst case to sort a sequence of n elements. Thus, merge sort and heapsort are asymptotically optimal, and no comparison sort exists that is faster by more than a constant factor.
(n lg n) comparisons in the worst case to sort a sequence of n elements. Thus, merge sort and heapsort are asymptotically optimal, and no comparison sort exists that is faster by more than a constant factor.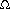 (n lg n) lower bound does not apply to them.
(n lg n) lower bound does not apply to them.9.1 Lower bounds for sorting
 a1, a2, . . . ,an) That is, given two elements ai and aj, we perform one of the tests ai < aj, ai
a1, a2, . . . ,an) That is, given two elements ai and aj, we perform one of the tests ai < aj, ai  aj, ai = aj, ai
aj, ai = aj, ai  aj, or ai > aj to determine their relative order. We may not inspect the values of the elements or gain order information about them in any other way.
aj, or ai > aj to determine their relative order. We may not inspect the values of the elements or gain order information about them in any other way. aj, ai
aj, ai  aj, ai > aj, and ai < aj are all equivalent in that they yield identical information about the relative order of ai and aj. We therefore assume that all comparisons have the form ai
aj, ai > aj, and ai < aj are all equivalent in that they yield identical information about the relative order of ai and aj. We therefore assume that all comparisons have the form ai  aj.
aj.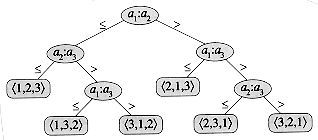
Figure 9.1 The decision tree for insertion sort operating on three elements. There are 3! = 6 possible permutations of the input elements, so the decision tree must have at least 6 leaves.
The decision-tree model
 i, j
i, j  n, where n is the number of elements in the input sequence. Each leaf is annotated by a permutation
n, where n is the number of elements in the input sequence. Each leaf is annotated by a permutation 
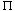 (1),
(1),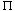 (2), . . . ,
(2), . . . ,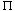 (n)
(n) . (See Section 6.1 for background on permutations.) The execution of the sorting algorithm corresponds to tracing a path from the root of the decision tree to a leaf. At each internal node, a comparison ai
. (See Section 6.1 for background on permutations.) The execution of the sorting algorithm corresponds to tracing a path from the root of the decision tree to a leaf. At each internal node, a comparison ai  aj is made. The left subtree then dictates subsequent comparisons for ai
aj is made. The left subtree then dictates subsequent comparisons for ai  aj, and the right subtree dictates subsequent comparisons for ai > aj. When we come to a leaf, the sorting algorithm has established the ordering a
aj, and the right subtree dictates subsequent comparisons for ai > aj. When we come to a leaf, the sorting algorithm has established the ordering a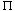 (1)
(1) a
a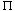 (2)
(2)  . . .
. . .  a
a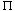 (n). Each of the n! permutations on n elements must appear as one of the leaves of the decision tree for the sorting algorithm to sort properly.
(n). Each of the n! permutations on n elements must appear as one of the leaves of the decision tree for the sorting algorithm to sort properly.A lower bound for the worst case
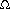 (n lg n).
(n lg n).n!
 2h ,
2h ,h
 lg(n!) ,
lg(n!) ,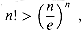
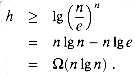
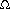 (n lg n) worst-case lower bound from Theorem 9.1.
(n lg n) worst-case lower bound from Theorem 9.1. Exercises
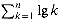 using techniques from Section 3.2.
using techniques from Section 3.2. (n lg n) lower bound for sorting n numbers does not apply to his computer environment, in which the control flow of a program can split three ways after a single comparison ai : aj, according to whether ai < aj, ai = aj, or ai > aj. Show that the professor is wrong by proving that the number of three-way comparisons required to sort n elements is still
(n lg n) lower bound for sorting n numbers does not apply to his computer environment, in which the control flow of a program can split three ways after a single comparison ai : aj, according to whether ai < aj, ai = aj, or ai > aj. Show that the professor is wrong by proving that the number of three-way comparisons required to sort n elements is still  (n lg n).
(n lg n). (n lg k) lower bound on the number of comparisons needed to solve this variant of the sorting problem. (Hint: It is not rigorous to simply combine the lower bounds for the individual subsequences.)
(n lg k) lower bound on the number of comparisons needed to solve this variant of the sorting problem. (Hint: It is not rigorous to simply combine the lower bounds for the individual subsequences.)9.2 Counting sort
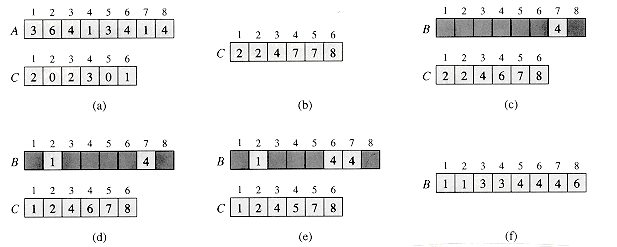
Figure 9.2 The operation of COUNTING-SORT on an input array A[1 . . 8], where each element ofA is a positive integer no larger than k = 6. (a) The array A and the auxiliary array C after line 4. (b) The array C after line 7. (c)-(e) The output array B and the auxiliary array C after one, two, and three iterations of the loop in lines 9-11, respectively. Only the lightly shaded elements of array B have been filled in. (f) The final sorted output array B.
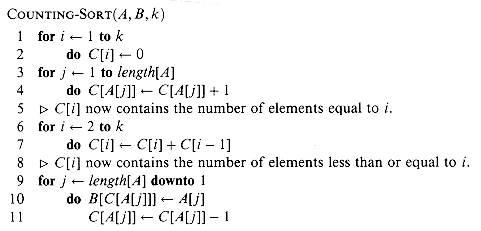
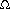 (n 1g n) proved in Section 9.1 because it is not a comparison sort. In fact, no comparisons between input elements occur anywhere in the code. Instead, counting sort uses the actual values of the elements to index into an array. The
(n 1g n) proved in Section 9.1 because it is not a comparison sort. In fact, no comparisons between input elements occur anywhere in the code. Instead, counting sort uses the actual values of the elements to index into an array. The 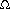 (n lg n) lower bound for sorting does not apply when we depart from the comparison-sort model.
(n lg n) lower bound for sorting does not apply when we depart from the comparison-sort model.Exercises
 7, 1, 3, 1, 2, 4, 5, 7, 2, 4, 3
7, 1, 3, 1, 2, 4, 5, 7, 2, 4, 3 .
.9 for j
 1 to length[A]
1 to length[A]9.3 Radix sort
329 720 720 329
457 355 329 355
657 436 436 436
839
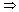 457
457 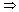 839
839  457
457436 657 355 657
720 329 457 720
355 839 657 839



Figure 9.3 The operation of radix sort on a list of seven 3-digit numbers. The first column is the input. The remaining columns show the list after successive sorts on increasingly significant digit positions. The vertical arrows indicate the digit position sorted on to produce each list from the previous one.
RADIX-SORT(A, d)
1 for i
 1 to d
1 to d2 do use a stable sort to sort array A on digit i
 (n + k). There are d passes, so the total time for radix sort is
(n + k). There are d passes, so the total time for radix sort is  (dn + kd). When d is constant and k = O(n), radix sort runs in linear time.
(dn + kd). When d is constant and k = O(n), radix sort runs in linear time. (lg n). For concreteness, let's say that d lg n is the number of bits, where d is a positive constant. Then, if each number to be sorted fits in one computer word, we can treat it as a d-digit number in radix-n notation. As a concrete example, consider sorting 1 million 64-bit numbers. By treating these numbers as four-digit, radix-2l6 numbers, we can sort them in just four passes using radix sort. This compares favorably with a typical
(lg n). For concreteness, let's say that d lg n is the number of bits, where d is a positive constant. Then, if each number to be sorted fits in one computer word, we can treat it as a d-digit number in radix-n notation. As a concrete example, consider sorting 1 million 64-bit numbers. By treating these numbers as four-digit, radix-2l6 numbers, we can sort them in just four passes using radix sort. This compares favorably with a typical  (n 1g n) comparison sort, which requires approximately 1g n = 20 operations per number to be sorted. Unfortunately, the version of radix sort that uses counting sort as the intermediate stable sort does not sort in place, which many of the
(n 1g n) comparison sort, which requires approximately 1g n = 20 operations per number to be sorted. Unfortunately, the version of radix sort that uses counting sort as the intermediate stable sort does not sort in place, which many of the  (n lg n) comparison sorts do. Thus, when primary memory storage is at a premium, an algorithm such as quicksort may be preferable.
(n lg n) comparison sorts do. Thus, when primary memory storage is at a premium, an algorithm such as quicksort may be preferable.Exercises
9.4 Bucket sort
 A[i] < 1. The code requires an auxiliary array B[0..n - 1] of linked lists (buckets) and assumes that there is a mechanism for maintaining such lists. (Section 11.2 describes how to implement basic operations on linked lists.)
A[i] < 1. The code requires an auxiliary array B[0..n - 1] of linked lists (buckets) and assumes that there is a mechanism for maintaining such lists. (Section 11.2 describes how to implement basic operations on linked lists.)
Figure 9.4 The operation of BUCKET-SORT. (a) The input array A[1 . .10]. (b) The array B[0 . . 9] of sorted lists (buckets) after line 5 of the algorithm. Bucket i holds values in the interval [i/10,(i + 1)/10). The sorted output consists of a concatenation in order of the lists B[0], B[1], . . . , B[9].
BUCKET-SORT(A)
1 n
 length [A]
length [A]2 for i
 1 to n
1 to n3 do insert A[ i] into list B [
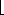 nA[i]
nA[i] ]
]4 for i
 0 to n -1
0 to n -15 do sort list B[i] with insertion sort
6 concatenate the lists B[0], B[1], . . . , B[n - 1] together in order
 A[j]. Assuming the contrary, we have
A[j]. Assuming the contrary, we havei' =
 nA[i]
nA[i]

 nA[j]
nA[j]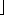
= j',
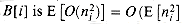 . The total expected time to sort all the elements in all the buckets is therefore
. The total expected time to sort all the elements in all the buckets is therefore
(9.1)

Exercises
 .79, .13, .16, .64, .39, .20, .89, .53, .71, .42
.79, .13, .16, .64, .39, .20, .89, .53, .71, .42 .
.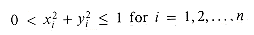 . Suppose that the points are uniformly distributed; that is, the probability of finding a point in any region of the circle is proportional to the area of that region. Design a
. Suppose that the points are uniformly distributed; that is, the probability of finding a point in any region of the circle is proportional to the area of that region. Design a  (n) expected-time algorithm to sort the n points by their distances
(n) expected-time algorithm to sort the n points by their distances 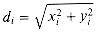 from the origin. (Hint: Design the bucket sizes in BUCKET-SORT to reflect the uniform distribution of the points in the unit circle.)
from the origin. (Hint: Design the bucket sizes in BUCKET-SORT to reflect the uniform distribution of the points in the unit circle.) x}. Suppose a list of n numbers has a continuous probability distribution function P that is computable in O(1) time. Show how to sort the numbers in linear expected time.
x}. Suppose a list of n numbers has a continuous probability distribution function P that is computable in O(1) time. Show how to sort the numbers in linear expected time.Problems
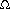 (n lg n) lower bound on the expected running time of any deterministic or randomized comparison sort on n inputs. We begin by examining a deterministic comparison sort A with decision tree TA. We assume that every permutation of A's inputs is equally likely.
(n lg n) lower bound on the expected running time of any deterministic or randomized comparison sort on n inputs. We begin by examining a deterministic comparison sort A with decision tree TA. We assume that every permutation of A's inputs is equally likely. i
i k {d (i)+d(k - i)+k}. (Hint: Consider a tree T with k leaves that achieves the minimum. Let i be the number of leaves in RT and k - i the number of leaves in LT.)
k {d (i)+d(k - i)+k}. (Hint: Consider a tree T with k leaves that achieves the minimum. Let i be the number of leaves in RT and k - i the number of leaves in LT.)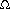 (k lg k).
(k lg k).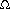 (n! lg(n!)) for TA, and conclude that the expected time to sort n elements is
(n! lg(n!)) for TA, and conclude that the expected time to sort n elements is 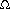 (n lg n).
(n lg n).Chapter notes