This chapter discusses two data structures that are constructed by augmenting red-black trees. Section 15.1 describes a data structure that supports general order-statistic operations on a dynamic set. We can then quickly find the ith smallest number in a set or the rank of a given element in the total ordering of the set. Section 15.2 abstracts the process of augmenting a data structure and provides a theorem that can simplify the augmentation of red-lack trees. Section 15.3 uses this theorem to help design a data structure for maintaining a dynamic set of intervals, such as time intervals. Given a query interval, we can then quickly find an interval in the set that overlaps it.
Chapter 10 introduced the notion of an order statistic. Specifically, the ith order statistic of a set of n elements, where i
A data structure that can support fast order-statistic operations is shown in Figure 15.1. An order-statistic tree T is simply a red-black tree with additional information stored in each node. Besides the usual red-black tree fields key[x], color[x], p[x], left[x], and right[x] in a node x, we have another field size[x]. This field contains the number of (internal) nodes in the subtree rooted at x (including x itself), that is, the size of the subtree. If we define size[NIL] to be 0, then we have the identity
(To handle the boundary condition for NIL properly, an actual implementation might test explicitly for NIL each time the size field is accessed or, more simply, as in Section 14.4, use a sentinel nil[T] to represent NIL, where size[nil[T]] = 0.)
Before we show how to maintain this size information during insertion and deletion, let us examine the implementation of two order-statistic queries that use this additional information. We begin with an operation that retrieves an element with a given rank. The procedure OS-SELECT(x, i) returns a pointer to the node containing the ith smallest key in the subtree rooted at x. To find the ith smallest key in an order-statistic tree T, we call OS-SELECT(root[T], i).
The idea behind OS-SELECT is similar to that of the selection algorithms in Chapter 10. The value of size[left[x]] is the number of nodes that come before x in an inorder tree walk of the subtree rooted at x. Thus, size[left[x]] + 1 is the rank of x within the subtree rooted at x.
In line 1 of OS-SELECT, we compute r, the rank of node x within the subtree rooted at x. If i = r, then node x is the ith smallest element, so we return x in line 3. If i < r, then the ith smallest element is in x's left subtree, so we recurse on left[x] in line 5. If i > r, then the ith smallest element is in x's right subtree. Since there are r elements in the subtree rooted at x that come before x's right subtree in an inorder tree walk, the ith smallest element in the subtree rooted at x is the (i - r)th smallest element in the subtree rooted at right[x]. This element is determined recursively in line 6.
To see how OS-SELECT operates, consider a search for the 17th smallest element in the order-statistic tree of Figure 15.1. We begin with x as the root, whose key is 26, and with i = 17. Since the size of 26's left subtree is 12, its rank is 13. Thus, we know that the node with rank 17 is the 17 - 13 = 4th smallest element in 26's right subtree. After the recursive call, x is the node with key 41, and i = 4. Since the size of 41's left subtree is 5, its rank within its subtree is 6. Thus, we know that the node with rank 4 is in the 4th smallest element in 41's left subtree. After the recursive call, x is the node with key 30, and its rank within its subtree is 2. Thus, we recurse once again to find the 4 - 2 = 2nd smallest element in the subtree rooted at the node with key 38. We now find that its left subtree has size 1, which means it is the second smallest element. Thus, a pointer to the node with key 38 is returned by the procedure.
Because each recursive call goes down one level in the order-statistic tree, the total time for OS-SELECT is at worst proportional to the height of the tree. Since the tree is a red-black tree, its height is O(lg n), where n is the number of nodes. Thus, the running time of OS-SELECT is O(lg n) for a dynamic set of n elements.
Given a pointer to a node x in an order-statistic tree T, the procedure OS-RANK returns the position of x in the linear order determined by an inorder tree walk of T.
The procedure works as follows. The rank of x can be viewed as the number of nodes preceding x in an inorder tree walk, plus 1 for x itself. The following invariant is maintained: at the top of the while loop of lines 3-6, r is the rank of key[x] in the subtree rooted at node y. We maintain this invariant as follows. In line 1, we set r to be the rank of key[x] within the subtree rooted at x. Setting y
As an example, when we run OS-RANK on the order-statistic tree of Figure 15.1 to find the rank of the node with key 38, we get the following sequence of values of key[y] and r at the top of the while loop:
The rank 17 is returned.
Since each iteration of the while loop takes O(1) time, and y goes up one level in the tree with each iteration, the running time of OS-RANK is at worst proportional to the height of the tree: O(lg n) on an n-node order-statistic tree.
Given the size field in each node, OS-SELECT and OS-RANK can quickly compute order-statistic information. But unless these fields can be efficiently maintained by the basic modifying operations on red-black trees, our work will have been for naught. We shall now show that subtree sizes can be maintained for both insertion and deletion without affecting the asymptotic running times of either operation.
We noted in Section 14.3 that insertion into a red-black tree consists of two phases. The first phase goes down the tree from the root, inserting the new node as a child of an existing node. The second phase goes up the tree, changing colors and ultimately performing rotations to maintain the red-black properties.
To maintain the subtree sizes in the first phase, we simply increment size[x] for each node x on the path traversed from the root down toward the leaves. The new node added gets a size of 1. Since there are O(lg n) nodes on the traversed path, the additional cost of maintaining the size fields is O(lg n).
In the second phase, the only structural changes to the underlying red-black tree are caused by rotations, of which there are at most two. Moreover, a rotation is a local operation: it invalidates only the two size fields in the nodes incident on the link around which the rotation is performed. Referring to the code for LEFT-ROTATE(T,x) in Section 14.2, we add the following lines:
Figure 15.2 illustrates how the fields are updated. The change to RIGHT-ROTATE is symmetric.
Since at most two rotations are performed during insertion into a red-black tree, only O(1) additional time is spent updating size fields in the second phase. Thus, the total time for insertion into an n-node order-statistic tree is O(lg n)--asymptotically the same as for an ordinary red-black tree.
Deletion from a red-black tree also consists of two phases: the first operates on the underlying search tree, and the second causes at most three rotations and otherwise performs no structural changes. (See Section 14.4.) The first phase splices out one node y. To update the subtree sizes, we simply traverse a path from node y up to the root, decrementing the size field of each node on the path. Since this path has length O(lg n) in an n-node red-black tree, the additional time spent maintaining size fields in the first phase is O(lg n). The O(1) rotations in the second phase of deletion can be handled in the same manner as for insertion. Thus, both insertion and deletion, including the maintenance of the size fields, take O(lg n) time for an n-node order-statistic tree.
15.1-1
Show how OS-SELECT(T, 10) operates on the red-black tree T of Figure 15.2.
15.1-2
Show how OS-RANK(T,x) operates on the red-black tree T of Figure 15.2 and the node x with key[x] = 35.
15.1-3
Write a nonrecursive version of OS-SELECT.
15.1-4
Write a recursive procedure OS-KEY-RANK(T,k) that takes as input an order-statistic tree T and a key k and returns the rank of k in the dynamic set represented by T. Assume that the keys of T are distinct.
15.1-5
Given an element x in an n-node order-statistic tree and a natural number i, how can the ith successor of x in the linear order of the tree be determined in O(lg n) time?
15.1-6
Observe that whenever the size field is referenced in either OS-SELECT or OS-RANK, it is only used to compute the rank of x in the subtree rooted at x. Accordingly, suppose we store in each node its rank in the subtree of which it is the root. Show how this information can be maintained during insertion and deletion. (Remember that these two operations can cause rotations.)
15.1-7
Show how to use an order-statistic tree to to count the number of inversions (see Problem 1-3) in an array of size n in time O(n lg n).
15.1-8
Consider n chords on a circle, each defined by its endpoints. Describe an O(n lg n)-time algorithm for determining the number of pairs of chords that intersect inside the circle. (For example, if the n chords are all diameters that meet at the center, then the correct answer is
The process of augmenting a basic data structure to support additional functionality occurs quite frequently in algorithm design. It will be used again in the next section to design a data structure that supports operations on intervals. In this section, we shall examine the steps involved in such augmentation. We shall also prove a theorem that allows us to augment red-black trees easily in many cases.
Augmenting a data structure can be broken into four steps:
1. choosing an underlying data structure,
2. determining additional information to be maintained in the underlying data structure,
3. verifying that the additional information can be maintained for the basic modifying operations on the underlying data structure, and
4. developing new operations.
As with any prescriptive design method, you should not blindly follow the steps in the order given. Most design work contains an element of trial and error, and progress on all steps usually proceeds in parallel. There is no point, for example, in determining additional information and developing new operations (steps 2 and 4) if we will not be able to maintain the additional information efficiently. Nevertheless, this four-step method provides a good focus for your efforts in augmenting a data structure, and it is also a good way to organize the documentation of an augmented data structure.
We followed these steps in Section 15.1 to design our order-statistic trees. For step 1, we chose red-black trees as the underlying data structure. A clue to the suitability of red-black trees comes from their efficient support of other dynamic-set operations on a total order, such as MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR.
For step 2, we provided the size fields, which in each node x stores the size of the subtree rooted at x. Generally, the additional information makes operations more efficient. For example, we could have implemented OS-SELECT and OS-RANK using just the keys stored in the tree, but they would not have run in O(lg n) time. Sometimes, the additional information is pointer information rather than data, as in Exercise 15.2-1.
For step 3, we ensured that insertion and deletion could maintain the size fields while still running in O(lg n) time. Ideally, a small number of changes to the data structure should suffice to maintain the additional information. For example, if we simply stored in each node its rank in the tree, the OS-SELECT and OS-RANK procedures would run quickly, but inserting a new minimum element would cause a change to this information in every node of the tree. When we store subtree sizes instead, inserting a new element causes information to change in only O(lg n) nodes.
For step 4, we developed the operations OS-SELECT and OS-RANK. After all, the need for new operations is why we bother to augment a data structure in the first place. Occasionally, rather than developing new operations, we use the additional information to expedite existing ones, as in Exercise 15.2-1.
When red-black trees underlie an augmented data structure, we can prove that certain kinds of additional information can always be efficiently maintained by insertion and deletion, thereby making step 3 very easy. The proof of the following theorem is similar to the argument from Section 15.1 that the size field can be maintained for order-statistic trees.
Theorem 15.1
Let â be a field that augments a red-black tree T of n nodes, and suppose that the contents of â for a node x can be computed using only the information in nodes x, left[x], and right[x], including â[left[x]] and â[right[x]]. Then, we can maintain the values of f in all nodes of T during insertion and deletion without asymptotically affecting the O(lg n) performance of these operations.
Proof The main idea of the proof is that a change to an â field in a node x propagates only to ancestors of x in the tree. That is, changing â[x] may require â[p[x]] to be updated, but nothing else; updating â[p[x]] may require â[p[p[x]]] to be updated, but nothing else; and so on up the tree. When â[root[T]] is updated, no other node depends on the new value, so the process terminates. Since the height of a red-black tree is O(lg n), changing an f field in a node costs O(lg n) time in updating nodes dependent on the change.
Insertion of a node x into T consists of two phases. (See Section 14.3.) During the first phase, x is inserted as a child of an existing node p[x]. The value for f[x] can be computed in O(1) time since, by supposition, it depends only on information in the other fields of x itself and the information in x's children, but x's children are both NIL. Once â[x] is computed, the change propagates up the tree. Thus, the total time for the first phase of insertion is O(lg n). During the second phase, the only structural changes to the tree come from rotations. Since only two nodes change in a rotation, the total time for updating theâ fields is O(lg n) per rotation. Since the number of rotations during insertion is at most two, the total time for insertion is O(lg n).
Like insertion, deletion has two phases. (See Section 14.4.) In the first phase, changes to the tree occur if the deleted node is replaced by its successor, and then again when either the deleted node or its successor is spliced out. Propagating the updates to f caused by these changes costs at most O(lg n) since the changes modify the tree locally. Fixing up the red-black tree during the second phase requires at most three rotations, and each rotation requires at most O(lg n) time to propagate the updates to f. Thus, like insertion, the total time for deletion is O(lg n).
In many cases, such as maintenance of the size fields in order-statistic trees, the cost of updating after a rotation is O(1), rather than the O(lg n) derived in the proof of Theorem 15.1. Exercise 15.2-4 gives an example.
15.2-1
Show how the dynamic-set queries MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR can each be supported in O(1) worst-case time on an augmented order-statistic tree. The asymptotic performance of other operations on order-statistic trees should not be affected.
15.2-2
Can the black-heights of nodes in a red-black tree be maintained as fields in the nodes of the tree without affecting the asymptotic performance of any of the red-black tree operations? Show how, or argue why not.
15.2-3
Can the depths of nodes in a red-black tree be efficiently maintained as fields in the nodes of the tree? Show how, or argue why not.
15.2-4
Let
15.2-5
We wish to augment red-black trees with an operation RB-ENUMERATE(x, a,b) that outputs all the keys k such that a< k
In this section, we shall augment red-black trees to support operations on dynamic sets of intervals. A closed interval is an ordered pair of real numbers [t1, t2], with t1
Intervals are convenient for representing events that each occupy a continuous period of time. We might, for example, wish to query a database of time intervals to find out what events occurred during a given interval. The data structure in this section provides an efficient means for maintaining such an interval database.
We can represent an interval [t1, t2] as an object i, with fields low[i] = t1 (the low endpoint) and high[i] = t2 (the high endpoint). We say that intervals i and i' overlap if
a. i and i' overlap,
b. high[i] < low[i'],
c. high[i'] < low[i].
Figure 15.3 shows the three possibilities.
An interval tree is a red-black tree that maintains a dynamic set of elements, with each element x containing an interval int[x]. Interval trees support the following operations.
INTERVAL-INSERT(T,x) adds the element x, whose int field is assumed to contain an interval, to the interval tree T.
INTERVAL-DELETE(T,x) removes the element x from the interval tree T.
INTERVAL-SEARCH(T,i) returns a pointer to an element x in the interval tree T such that int[x] overlaps interval i, or NIL if no such element is in the set.
Figure 15.4 shows how an interval tree represents a set of intervals. We shall track the four-step method from Section 15.2 as we review the design of an interval tree and the operations that run on it.
We choose a red-black tree in which each node x contains an interval int[x] and the key of x is the low endpoint, low[int[x]], of the interval. Thus, an inorder tree walk of the data structure lists the intervals in sorted order by low endpoint.
In addition to the intervals themselves, each node x contains a value max[x], which is the maximum value of any interval endpoint stored in the subtree rooted at x. Since any interval's high endpoint is at least as large as its low endpoint, max[x] is the maximum value of all right endpoints in the subtree rooted at x.
We must verify that insertion and deletion can be performed in O(lg n) time on an interval tree of n nodes. We can determine max[x] given interval int[x] and the max values of node x's children:
Thus, by Theorem 15.1, insertion and deletion run in O(lg n) time. In fact, updating the max fields after a rotation can be accomplished in O(1) time, as is shown in Exercises 15.2-4 and 15.3-1.
The only new operation we need is INTERVAL-SEARCH(T, i), which finds an interval in tree T that overlaps interval i. If there is no interval that overlaps i in the tree, NIL is returned.
The search for an interval that overlaps i starts with x at the root of the tree and proceeds downward. It terminates when either an overlapping interval is found or x becomes NIL. Since each iteration of the basic loop takes O(1) time, and since the height of an n-node red-black tree is O(lg n), the INTERVAL-SEARCH procedure takes O(lg n) time.
Before we see why INTERVAL-SEARCH is correct, let's examine how it works on the interval tree in Figure 15.4. Suppose we wish to find an interval that overlaps the interval i = [22, 25]. We begin with x as the root, which contains [16,21] and does not overlap i. Since max[left[x]] = 23 is greater than low[i] = 22, the loop continues with x as the left child of the root--the node containing [8, 9], which also does not overlap i. This time, max[left[x]] = 10 is less than low[i] = 22, so the loop continues with the right child of x as the new x. The interval [15, 23] stored in this node overlaps i, so the procedure returns this node.
As an example of an unsuccessful search, suppose we wish to find an interval that overlaps i = [11, 14] in the interval tree of Figure 15.4. We once again begin with x as the root. Since the root's interval [16, 21] does not overlap i, and since max[left[x]] = 23 is greater than low[i] = 11, we go left to the node containing [8, 9]. (Note that no interval in the right subtree overlaps i--we shall see why later.) Interval [8, 9] does not overlap i, and max[left[x]] = 10 is less than low[i] = 11, so we go right. (Note that no interval in the left subtree overlaps i.) Interval [15, 23] does not overlap i, and its left child is NIL, so we go right, the loop terminates, and NIL is returned.
To see why INTERVAL-SEARCH is correct, we must understand why it suffices to examine a single path from the root. The basic idea is that at any node x, if int[x] does not overlap i, the search always proceeds in a safe direction: an overlapping interval will definitely be found if there is one in the tree. The following theorem states this property more precisely.
Theorem 15.2
Consider any iteration of the while loop during the execution of INTERVAL-SEARCH(T, i).
1. f line 4 is executed (the search goes left), then x's left subtree contains an interval that overlaps i or no interval in x's right subtree overlaps i.
2. If line 5 is executed (the search goes right), then x's left subtree contains no interval that overlaps i.
Proof The proof of both cases depend on the interval trichotomy. We prove case 2 first, since it is simpler. Observe that if line 5 is executed, then because of the branch condition in line 3, we have left[x] = NIL, or max[left[x]] < low[i]x. If left[x] = NIL, the subtree rooted at left[x] clearly contains no interval that overlaps i, because it contains no intervals at all. Suppose, therefore, that left[x]
and thus, by the interval trichotomy, i' and i do not overlap, which completes the proof of case 2.
To prove case 1, we may assume that no intervals in x's left subtree overlap i (since if any do, we are done), and thus we need only prove that no intervals in x's right subtree overlap i under this assumption. Observe that if line 4 is executed, then because of the branch condition in line 3, we have max[left[x]]
there must be some interval i' in x's left subtree such that
(Figure 15.5(b) illustrates the situation.) Since i and i' do not overlap, and since it is not true that high[i'] < low[i], it follows by the interval trichotomy that high[i] < low[i']. Interval trees are keyed on the low endpoints of intervals, and thus the search-tree property implies that for any interval i" in x's right subtree,
By the interval trichotomy, i and i" do not overlap.
Theorem 15.2 guarantees that if INTERVAL-SEARCH continues with one of x's children and no overlapping interval is found, a search starting with x's other child would have been equally fruitless.
15.3-1
Write pseudocode for LEFT-ROTATE that operates on nodes in an interval tree and updates the max fields in O(1) time.
15.3-2
Rewrite the code for INTERVAL-SEARCH so that it works properly when all intervals are assumed to be open.
15.3-3
Describe an efficient algorithm that, given an interval i, returns an interval overlapping i that has the minimum low endpoint, or NIL if no such interval exists.
15.3-4
Given an interval tree T and an interval i, describe how all intervals in T that overlap i can be listed in O(min(n, k 1g n)) time, where k is the number of intervals in the output list. (Optional: Find a solution that does not modify the tree.)
15.3-5
Suggest modifications to the interval-tree procedures to support the operation INTERVAL-SEARCH-EXACTLY(T, i), which returns a pointer to a node x in interval tree T such that low[int]x]] = low[i] and high[int[x]] = high[i], or NIL if T contains no such node. All operations, including INTERVAL-SEARCH-EXACTLY, should run in O(1g n) time on an n-node tree.
15.3-6
Show how to maintain a dynamic set Q of numbers that supports the operation MIN-GAP, which gives the magnitude of the difference of the two closest numbers in Q. For example, if Q = {1, 5, 9, 15, 18, 22}, then MIN-GAP(Q) returns 18 - 15 = 3, since 15 and 18 are the two closest numbers in Q. Make the operations INSERT, DELETE, SEARCH, and MIN-GAP as efficient as possible, and analyze their running times.
15.3-7
VLSI databases commonly represent an integrated circuit as a list of rectangles. Assume that each rectangle is rectilinearly oriented (sides parallel to the x- and y-axis), so that a representation of a rectangle consists of its minimum and maximum x- and y-coordinates. Give an O(n 1g n)-time algorithm to decide whether or not a set of rectangles so represented contains two rectangles that overlap. Your algorithm need not report all intersecting pairs, but it must report that an overlap exists if one rectangle entirely covers another, even if the boundary lines do not intersect. (Hint: Move a "sweep" line across the set of rectangles.)
15-1 Point of maximum overlap
Suppose that we wish to keep track of a point of maximum overlap in a set of intervals--a point that has the largest number of intervals in the database overlapping it. Show how the point of maximum overlap can be maintained efficiently while intervals are inserted and deleted.
15-2 Josephus permutation
The Josephus problem is defined as follows. Suppose that n people are arranged in a circle and that we are given a positive integer m
a. Suppose that m is a constant. Describe an O(n)-time algorithm that, given an integer n, outputs the (n, m)-Josephus permutation.
b. Suppose that m is not a constant. Describe an O(n 1g n)-time algorithm that, given integers n and m, outputs the (n, m)-Josephus permutation.
Preparata and Shamos [160] describe several of the interval trees that appear in the literature. Among the more important theoretically are those due independently to H. Edelsbrunner (1980) and E. M. McCreight (1981), which, in a database of n intervals, allow all k intervals that overlap a given query interval to be enumerated in O(k + 1g n) time.
15.1 Dynamic order statistics
 { 1, 2, . . ., n}, is simply the element in the set with the ith smallest key. We saw that any order statistic could be retrieved in O(n) time from an unordered set. In this section, we shall see how red-black trees can be modified so that any order statistic can be determined in O(lg n) time. We shall also see how the rank of an element--its position in the linear order of the set--can likewise be determined in O(lg n) time.
{ 1, 2, . . ., n}, is simply the element in the set with the ith smallest key. We saw that any order statistic could be retrieved in O(n) time from an unordered set. In this section, we shall see how red-black trees can be modified so that any order statistic can be determined in O(lg n) time. We shall also see how the rank of an element--its position in the linear order of the set--can likewise be determined in O(lg n) time.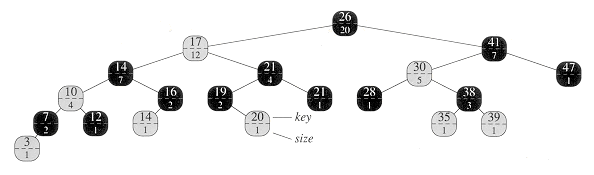
Figure 15.1 An order-statistic tree, which is an augmented red-black tree. Shaded nodes are red, and darkened nodes are black. In addition to its usual fields, each node x has a field size[x], which is the number of nodes in the subtree rooted at x.
size[x] = size[left[x]] + size[right[x]] + 1 .
Retrieving an element with a given rank
OS-SELECT(x,i)
1 r
 size[left[x]] + 1
size[left[x]] + 12 if i = r
3 then return x
4 elseif i < r
5 then return OS-SELECT(left[x],i)
6 else return OS-SELECT(right[x],i - r)
Determining the rank of an element
OS-RANK(T,x)
1 r
 size[left[x]] + 1
size[left[x]] + 12 y
 x
x3 while y
 root[T]
root[T]4 do if y = right[p[y]]
5 then r
 r + size[left[p[y]]] + 1
r + size[left[p[y]]] + 16 y
 p[y]
p[y]7 return r
 x in line 2 makes the invariant true the first time the test in line 3 executes. In each iteration of the while loop, we consider the subtree rooted at p[y]. We have already counted the number of nodes in the subtree rooted at node y that precede x in an inorder walk, so we must add the nodes in the subtree rooted at y's sibling that precede x in an inorder walk, plus 1 for p[y] if it, too, precedes x. If y is a left child, then neither p[y] nor any node in p[y]'s right subtree precedes x, so we leave r alone. Otherwise, y is a right child and all the nodes in p[y]'s left subtree precede x, as does p[y] itself. Thus, in line 5, we add size[left[y]] + 1 to the current value of r Setting y
x in line 2 makes the invariant true the first time the test in line 3 executes. In each iteration of the while loop, we consider the subtree rooted at p[y]. We have already counted the number of nodes in the subtree rooted at node y that precede x in an inorder walk, so we must add the nodes in the subtree rooted at y's sibling that precede x in an inorder walk, plus 1 for p[y] if it, too, precedes x. If y is a left child, then neither p[y] nor any node in p[y]'s right subtree precedes x, so we leave r alone. Otherwise, y is a right child and all the nodes in p[y]'s left subtree precede x, as does p[y] itself. Thus, in line 5, we add size[left[y]] + 1 to the current value of r Setting y  p[y] makes the invariant true for the next iteration. When y = root[T], the procedure returns the value of r, which is now the rank of key[x].
p[y] makes the invariant true for the next iteration. When y = root[T], the procedure returns the value of r, which is now the rank of key[x]. iteration key[y] r
--------------------
1 38 2
2 30 4
3 41 4
4 26 17
Maintaining subtree sizes
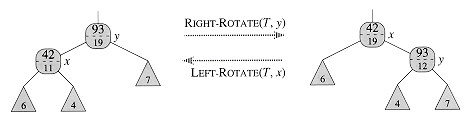
Figure 15.2 Updating subtree sizes during rotations. The two size fields that need to be updated are the ones incident on the link around which the rotation is performed. The updates are local, requiring only the size information stored in x, y, and the roots of the subtrees shown as triangles.
13 size[y]
 size[x]
size[x]14 size[x]
 size[left[x]] + size[right[x]] + 1
size[left[x]] + size[right[x]] + 1Exercises
 .) Assume that no two chords share an endpoint.
.) Assume that no two chords share an endpoint.15.2 How to augment a data structure
Augmenting red-black trees
Exercises
 be an associative binary operator, and let a be a field maintained in each node of a red-black tree. Suppose that we want to include in each node x an additional field
be an associative binary operator, and let a be a field maintained in each node of a red-black tree. Suppose that we want to include in each node x an additional field 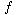 such that
such that 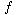 [x] = a[x1]
[x] = a[x1]  a[x2],
a[x2], 



 a[xm], where x1, x2, . . . , xm is the inorder listing of nodes in the subtree rooted at x. Show that the
a[xm], where x1, x2, . . . , xm is the inorder listing of nodes in the subtree rooted at x. Show that the 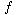 fields can be properly updated in O(1) time after a rotation. Modify your argument slightly to show that the size fields in order-statistic trees can be maintained in O(1) time per rotation.
fields can be properly updated in O(1) time after a rotation. Modify your argument slightly to show that the size fields in order-statistic trees can be maintained in O(1) time per rotation. b in a red-black tree rooted at x. Describe how RB-ENUMERATE can be implemented in
b in a red-black tree rooted at x. Describe how RB-ENUMERATE can be implemented in  (m + lg n) time, where m is the number of keys that are output and n is the number of internal nodes in the tree. (Hint: There is no need to add new fields to the red-black tree.)
(m + lg n) time, where m is the number of keys that are output and n is the number of internal nodes in the tree. (Hint: There is no need to add new fields to the red-black tree.)15.3 Interval trees
 t2. The interval [t1, t2] represents the set {t
t2. The interval [t1, t2] represents the set {t  R: t1
R: t1  t
t  t2}. Open and half-open intervals omit both or one of the endpoints from the set, respectively. In this section, we shall assume that intervals are closed; extending the results to open and half-open intervals is conceptually straightforward.
t2}. Open and half-open intervals omit both or one of the endpoints from the set, respectively. In this section, we shall assume that intervals are closed; extending the results to open and half-open intervals is conceptually straightforward.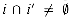 , that is, if low[i]
, that is, if low[i]  high[i'] and low[i']
high[i'] and low[i']  high[i]. Any two intervals i and i' satisfy the interval trichotomy; that is, exactly one of the following three properties holds:
high[i]. Any two intervals i and i' satisfy the interval trichotomy; that is, exactly one of the following three properties holds: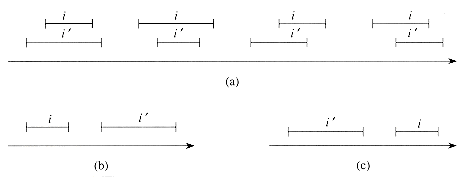
Figure 15.3 The interval trichotomy for two closed intervals i and i'. (a) If i and i'overlap, there are four situations; in each, low[i]
 high[i'] and low[i']
high[i'] and low[i']  high[i]. (b) high[i] < low[i']. (c) high[i'] < low[i].
high[i]. (b) high[i] < low[i']. (c) high[i'] < low[i].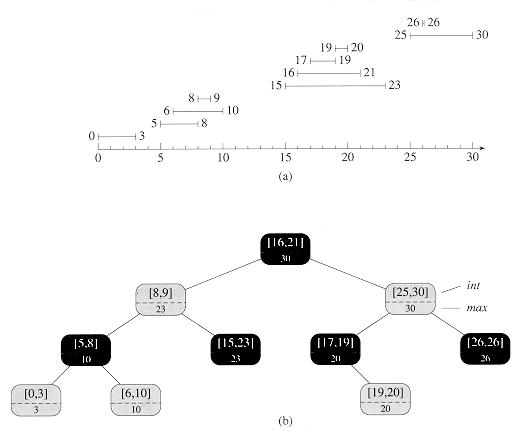
Figure 15.4 An interval tree. (a) A set of 10 intervals, shown sorted bottom to top by left endpoint. (b) The interval tree that represents them. An inorder tree walk of the tree lists the nodes in sorted order by left endpoint.
Step 1: Underlying data structure
Step 2: Additional information
Step 3: Maintaining the information
max[x] = max(high[int[x]], max[left[x]], max[right[x]]).
Step 4: Developing new operations
INTERVAL-SEARCH(T,i)
1 x
 root[T]
root[T]2 while x
 NIL and i does not overlap int[x]
NIL and i does not overlap int[x]3 do if left[x]
 NIL and max[left[x]]
NIL and max[left[x]]  low[i]
low[i]4 then x
 left[x]
left[x]5 else x
 right[x]
right[x]6 return x
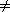 NIL and max[left]x]] < low[i]. Let i' be an interval in x's left subtree. (See Figure 15.5(a).) Since max[left[x]] is the largest endpoint in x's left subtree, we have
NIL and max[left]x]] < low[i]. Let i' be an interval in x's left subtree. (See Figure 15.5(a).) Since max[left[x]] is the largest endpoint in x's left subtree, we havehigh[i']
 max[left[x]]
max[left[x]]< low[i] ,
 low[i]. Moreover, by definition of the max field,
low[i]. Moreover, by definition of the max field,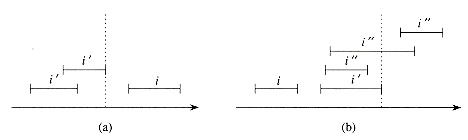
Figure 15.5 Intervals in the proof of Theorem 15.2. The value of max[left[x]] is shown in each case as a dashed line. (a) Case 2: the search goes right. No interval i' can overlap i. (b) Case 1: the search goes left. The left subtree of x contains an interval that overlaps i (situation not shown), or there is an interval i' in x's left subtree such that high[i'] = max[left[x]]. Since i does not overlap i', neither does it overlap any interval i\" in x' s right subtree, since low[i']
 low[i\"].
low[i\"].high[i'] = max[left[x]]
 low[i].
low[i].high[i] < low[i']
 low[i"].
low[i"].Exercises
Problems
 n. Beginning with a designated first person, we proceed around the circle, removing every mth person. After each person is removed, counting continues around the circle that remains. This process continues until all n people have been removed. The order in which the people are removed from the circle defines the (n, m)-Josephus permutation of the integers 1, 2, . . . , n. For example, the (7, 3)-Josephus permutation is < 3, 6, 2, 7, 5, 1, 4 > .
n. Beginning with a designated first person, we proceed around the circle, removing every mth person. After each person is removed, counting continues around the circle that remains. This process continues until all n people have been removed. The order in which the people are removed from the circle defines the (n, m)-Josephus permutation of the integers 1, 2, . . . , n. For example, the (7, 3)-Josephus permutation is < 3, 6, 2, 7, 5, 1, 4 > .Chapter notes


