char *p;
p = malloc(N);
will set aside a contiguous "chunk" of N bytes of data storage and return the address of this chunk to be stored in the pointer p. This memory is guaranteed not to overlap the storage of any declared variable or any other memory obtained by the allocation functions.
Besides the malloc function, there is also a calloc function, which behaves like malloc with two extra features: the allocated memory is filled with 0-bits, and the number of bytes requested is given by the product of the two arguments.
will cause p to point to a new chunk of N * M bytes filled with zeroes.
The conventional term for the location of allocated storage is the heap. In many environments, the heap starts at the low addresses of the dynamic data segment and grows upwards to high addresses, while the stack starts at high addresses and grows downwards. If a function call needs more stack space than the dynamic segment has available for it ("stack-heap collision"), this is a fatal error. Nothing reliable can happen afterwards. Most environments will terminate the program with a severe error.
If a request for allocated memory asks for more bytes than are available in the heap, the malloc (or calloc) function returns a NULL pointer. Thus, the returned pointer should always be tested to be sure that it is non-NULL. Moreover, early in the program design, if the program uses dynamic memory allocation, an error-handling strategy must be determined for the "out-of-heap" condition. (On many non-UNIX systems, it is necessary to specify a maximum size for the program's dynamic memory; the details depend upon the environment [7-1].)
When allocation is successful, the memory provided will have the most restrictive alignment of any data type on the target machine. In other words, it is safe to store any kind of data in the allocated memory, because the alignment will always be adequate.
One of the most common uses of dynamic allocation is storing a structure. In this case, the pointer by which we will access the memory will be a pointer to some type of structure, and the returned pointer from malloc (or calloc) should be cast to the type of the pointer:
When allocated storage has been used and is no longer needed, it can be returned to the heap by the free function:
will give back to the heap the storage which px is pointing to. Note carefully that each time storage is allocated, the allocation functions record internally the size that was given to this allocation. When free is called, this internally-recorded size is used to determine the amount of storage that is being given back. It is very important that the pointer value passed to the free function must be one which was originally delivered by malloc (or calloc).
One of the important reliability aspects of dynamic allocation is the avoidance of dangling pointers. After calling free(px), the pointer px should be considered to have an undefined value. To be sure, the pointer does still contain a valid machine address, but the storage that it points to may subsequently be allocated to some other use. One useful style convention is to immediately assign NULL to a pointer after passing it to the free function:
In some environments, this will ensure that any further access using px will generate an execution error [7-2]. And in any environment, it will warn the reader that px should not be used to access data.
This convention is not a complete preventative measure by itself, because more than one pointer may be pointing to the freed storage. Here is a more general rule:
Rule 7-1: When a pointer p is passed to the free function, the programmer must determine how many pointers are pointing into the freed storage. (This number is known as the "reference count" of the storage.) Steps must be taken (such as assigning NULL) to ensure that none of these pointers are subsequently used to access the freed storage.
We have seen that a "dangling pointer" results from continued use of a pointer to freed storage. There is a complementary problem known as dead storage which results from failure to free a chunk of storage when it is no longer needed. Here is an unusually blatant case of dead storage:
Access to the allocated storage is immediately lost, and there is no way to let the allocation functions know that the storage is available for other uses. A few isolated cases of dead storage are unlikely to be noticed; the storage available is simply decreased. But as the dead storage begins to accumulate, the odds increase that the program will run out of allocatable storage. The preventive measures are fairly simple:
Rule 7-2: For every instance in which a program allocates storage, there should be an easily identifiable instance in which that storage is later freed.
A structure can contain a pointer to the same type of structure, which is useful for building data structures which can grow and shrink during execution. The simplest such data structure is a singly-linked list, or chain.
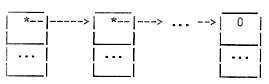
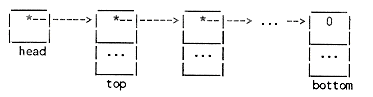
Each box represents a node on the stack. Each node contains a pointer to another node; we will conventionally name this member of the node structure the next pointer. The bottom node is distinguished by having a null next pointer. In the other nodes, the next pointer points one node further down the chain.
One common use of a chain (singly-linked list) is to implement a stack, a data structure where insertions and deletions take place at one end, called the "top" of the stack. Thus, one pointer (pointing to the top node) is all that is needed to access the stack.
Note that we have here a situation very similar to the use of pointers to access an array: the indirect object of the head pointer (the thing that it points to, syntactically) is one single object, but it is being used to provide access to several such objects. When the data structure being accessed through head is a stack, we will often use the verbal shorthand of saying that head is a stack.
For the time being, we will use an array of four char'S as the data portion of each node in the stack.
Throughout this chapter, each structure template will contain one or more pointers to other structures of the same type. Declarations of such structure templates look more uniform if the #define method is used, rather than the typedef method, because the typedef method does not allow us to use the structure's uppercase name inside its own declaration:
With the typedef method, the name ST_NODE is not available for use inside the structure itself, because the name is not seen by the compiler until the end of the declaration. The comparison is aesthetic, not substantive; use whichever form you like. The declaration of the stack node template will go into a stack.h header, along with the declaration of some functions to appear shortly.
A new (empty) stack can be created simply by assigning (or initializing) NULL to a "head" pointer:
The treatment of different data structures will be made easier, however, if we define a macro ST_OPEN which accepts a pointer to the head pointer (a ST_NODE ** parameter), and assign NULL to the head pointer:
Then the "opening" of a stack is accomplished via
To avoid special cases in the processing of dynamic structures, we will make sure that each node in a structure is well-defined, i.e., all members are well-defined. Thus, no "garbage" values will be found within the structure. The invariant properties of a singly-linked stack can therefore be expressed like this:
0. If head == NULL, the stack is empty, i.e., contains no nodes.
N. Otherwise, head points to a well-defined ST_NODE; this is the "first" or "top" node in the stack. Some node, node-N, has a NULL next- pointer; this is the "last" or "bottom" node in the stack. The stack accessed through head consists of the N nodes reachable via the chain of next-pointers. Every ST_NODE in the stack is well-defined.
The basic operations upon a stack are "pushing" a node onto the stack, and "popping" a node off the stack. The simplest implementation is obtained by requiring the user's calling function to allocate the space for a new node before calling the "push" function. And the "pop" function will detach a node from the stack and hand it to the calling function. It is thus up to the calling function to free the node's storage when it is needed no further.
The head pointer will also belong to the calling function. This allows the stack functions to be invoked upon several different stacks, but requires that each function must accept the value or the address of the head pointer as a parameter of each function. In this example, both the st_push and st_pop functions must modify the head pointer, so they must be passed its address. This is the st_push function:
And this is the st_pop function:
Let us pause to examine the types of the pointers and expressions. The parameter headp is declared to have the type ST_NODE **, i.e., pointer to pointer to ST_NODE. The expression *headp thus has the type ST_NODE *, or pointer to ST_NODE. And p->next is the next member of the node that p points to. Its type is also ST_NODE *.
Also notice in the st_pop function that we assign NULL to the next member of the popped node, before turning the node over to the calling function. This will ensure that the popped node is not used to provide further access to the stack, whose structure may subsequently be altered by further pushes and pops.
To close a singly-linked stack, we must free any nodes which remain in the stack. We must then assign NULL to its head pointer.
A simple for loop can step a pointer over each of the nodes on the stack:
This operation -- looping a pointer over each node in a data structure -- will be useful for each data structure, so we will define a macro
which we can use like this:
Three other macros will be useful: ST_IS_EMPTY(head) produces YES if the stack is empty, NO otherwise; ST_FIRST(head) produces a pointer to the first node on the stack; and ST_NEXT(p) produces a pointer to the ("successor") node that follows the node pointed to by p:
This completes the list of operations needed to implement a stack as a singly-linked list. As configured, however, the stack works for only one specific type of node, one in which the data member is an array of four charS. We would prefer for our data structure operations to be more general than this, even at the expense of the simplicity of the implementation. After all, we will create the data structure headers and functions only once but we will use them many different times in different contexts.
The packaging approach that we will show in this chapter will allow the data structure functions and macros to be used upon any structure whose initial members contain the proper pointers. We will, for example, generalize the "stack" package to allow it to be used upon any structure whose first member is a pointer to other such structures, and the name of the first member must be next. The stack.h header will contain a declaration of an ST_NODE that looks like this:
Suppose, then, that we wish to use the "stack" package with nodes that look like this:
A macro like ST_NEXT will generate the proper code when applied to NAME_NODES: ST_NEXT(name_head) becomes ((name_head)->next) as desired. When calling the functions, such as st_push, there is a type-matching problem to solve. A type-checking environment such as lint will notice that we are passing a pointer to NAME_NODE'S to a function that expects pointers to ST_NODES, and will properly complain. Since we know that the two structures are in fact compatible with each other for the uses that are being made within the function, we will add macros to the stack.h which call the function with pointer arguments that have had the proper casts applied to them.
It will also be useful to provide in each data structure header any appropriate "non-NULL" tests for each pointer argument. If the tests are conditional upon NDEBUG they will not slow down the execution version of the system. Since we will make use of the non-NULL tests and the pointer casts in several different data-structure headers, we will make a header, pointer.h, for these useful pointer operations:
We can now show the contents of the stack.h header:
Consider the ST_CLOSE macro. It makes use of an auxiliary macro named ST_PP which ensures that its argument is non-NULL and casts it to the type ST_NODE ** (pointer to pointer to ST_NODE). The macros ST_POP and ST_PUSH are similarly implemented.
The end result of all this packaging is that we can use the "stack" package with any structure that has a next pointer as its first member. All the operations are provided as macros that have uniform uppercase names beginning with "ST_."
In order to give a simple demonstration of the stack functions, we will create a small interactive program, st_main.c:
We are handling the "out-of-heap" condition by simple "diagnose-and-terminate" logic. This is adequate for simple interactive uses.
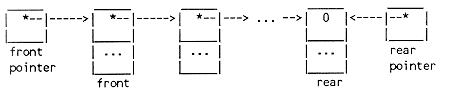
With a small modification to the stack structure, we obtain a data structure that allows insertion at the one end and deletion at the other -- a queue, that is.
The properties of a queue are similar to those of a stack:
0. If either front or rear is NULL, both are NULL, and the queue is empty, i.e., contains no nodes.
N. Otherwise, front points to a well-defined node; this is the "first" or "front" node in the queue. Some node, node-N, has a NULL next-pointer; this is the "last" or "rear" node in the queue, and rear points to this node. The queue accessed through front and rear contains the N nodes reachable via the chain of next-pointers. Every Q_NODE in the queue is well-defined, i.e., all its members are well-defined.
The data structure itself is the same singly-linked list that we used for the stack; we have just added a second access pointer at the "rear." The operation of "opening" a queue assigns NULL to both the front and the rear pointers:
As with the stack, the "first" and "next" operations are simple macros:
A queue can be "popped" just like a stack: simply detach the first node. (When the single remaining node is popped, the rear pointer must be set to NULL.)
However, we can define a somewhat more general operation, "detach to the right." Define the link-in of a node on a queue as that pointer which points to it. Specifically, the link-in to the first node is the front pointer; the link-in of each other node is the next pointer of the node to its left. Given a pointer to a link-in, we can detach the node to the right of the link-in:
A node can be "pushed" onto a queue (impolite, but useful sometimes), just as with a stack, except that the rear pointer must be set when the new node is the first arrival onto an empty queue.
As with "pop," the "push" is a special case of inserting a node to the right of a pointer which becomes the node's link-in:
The queue allows an "append" operation, an insertion onto the end of the queue:
The "close" operation must free all remaining nodes and assign NULL to both front and rear pointers:
The macro EACH_Q behaves the same as the EACH_ST macro did:
A queue is empty if its front pointer is NULL:
A queue can conveniently be used to store an ordered list of nodes; we will soon see a queue of tasks stored in order of the time that they are supposed to be performed. In order for an "ordered insert" function to be general-purpose, it must accept a pointer to a comparison function, just as we saw in the "quicksort" examples:
A "find" function is also easy, given a comparison function pointer. It will, however, be more useful for the "find" operation to produce a pointer to the link-in of the found node, since the link-in is necessary for insertions or deletions inside the queue:
Access to all these operations is provided by the header for the queue package:
A queue is a convenient data structure to use for a list of tasks to be performed. Each task has a specified "start time," and can be inserted into the proper chronological position in the queue.
Here is a program which will accept the following transactions: insert a task into the queue, print the task with the earliest start time and remove it from the queue, print all tasks on the queue.
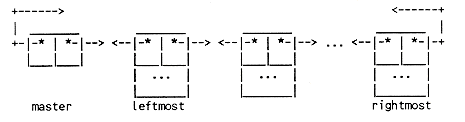
A "double-ended queue" or deque is a data structure in which each node has two pointers, one forward and one backward. Thus, it is also known as a "doubly-linked list."
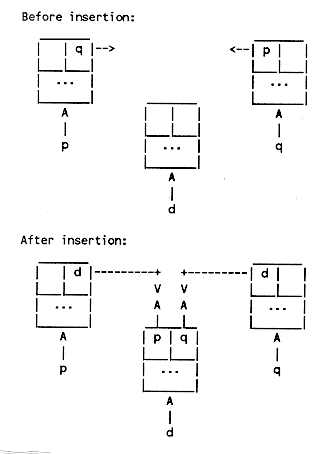
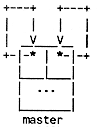
A deque is often implemented with an extra node which contains no data but serves to make the operations more uniform; we will call this node a master node. A picture may help:
Given a pointer to any node, it is possible to reach all the other nodes by traversing pointers.
A node can be inserted to the right or to the left of any other node; all that is required is a pointer to the new node and a pointer to the insertion point. The following picture shows the insertion of the node d (i.e., the node pointed to by pointer d), to the right of node p, or to the left of node q. (Either p or q is adequate; either can be determined from the other.)
It is possible to remove a node from a deque given nothing more than a pointer to the node itself. Referring to the "after insertion" diagram above, given the pointer d, the nodes to the left and right can be located using information in the node *d. Thus, a deletion is just the exact reversal of an insertion.
An empty deque consists of one node, the master node, whose left and right pointers both point to itself:
Thus, even in the empty deque, the master node has a left and right node (itself). There are no special cases in the insertion logic. To implement the deletion logic, the only special case is that the master node should not be freed; the manipulation of left and right pointers is the same for the deletion of any node.
Having a master node makes the calling sequence of the deque operations much more uniform. In the header deque.h will appear a type definition for the name DQ_NODE, defined like this:
All the nodes in the deque, including the master, conform to this template. Since the master node is not a data node, we can require that the calling program must refer to the master node as a DQ_NODE, rather than as a data node. Thus, any program using the "deque" package must provide a "head" pointer which points to DQ_NODES.
These are the properties of a deque:
0. If the left or right pointer of the master node contains the address of the master node itself, then both do, and the deque is empty, i.e., contains no data nodes.
N. Otherwise, the right pointer of the master node points to a well-defined node; this is the "first" node in the deque. Some node, node-N, has a right pointer which points to the master node. The deque consists of the N nodes reachable via the chain of right-pointers, from the first node to node-N. For each node a in the deque, the node to the right of node a has a left-pointer that points back to a. Every node in the deque is well-defined, i.e., all its members are well-defined.
The operations dq_open and dq_close will alter the deque pointer and must be given its address, a "pointer to pointer to DQ_NODE" value. Most of the other operations will take a "pointer to DQ_NODE" first argument. Here are the dq_open and dq_close functions:
The dq_close function frees any nodes remaining in the deque, including the master node.
Deques are often used to represent "circular lists," where the first node is considered to be the successor of the last node. The master node is not a data node, so is not to be considered part of the circular list. (As in the other headers, we make use of the macro PNN -- "pointer non-NULL" -- to provide debugging assistance in preventing NULL pointer bugs.)
Detaching a node requires only a pointer to the node itself. The function does not allow the master node to be detached; a NULL pointer is returned if an attempt is made to detach the master node.
The operation "insert to the right of" was shown in the diagrams earlier. Because of the master node, there are no special cases in the insertion logic.
Consistent with our adopted packaging, a macro DQ_R_INSERT is provided which verifies that pointers are non-NULL and casts them to the appropriate types:
Insertion to the left of node p is most simply implemented by inserting to the right of node p->left:
The operation DQ_PUSH is trivial; it simply uses DQ_R_INSERT. In other words, to "push" node d onto deque dq, simply insert d after dq:
The dq_pop function returns NULL if the deque is empty (no nodes except the master node). Otherwise, it detaches the node to the right of the master node.
The work of DQ_APPEND is accomplished by inserting node d to the right of the last node in the deque:
The test for "emptiness" of a deque is whether the node to the right of the master node is the master node itself:
The operations dq_insert and dq_find (which require a cmpfn pointer to provide the ordering function) are similar to the corresponding queue functions, except that the end of the list is marked by reaching the master node instead of reaching a NULL pointer. Another difference is that the dq_find function can simply return a pointer to the found node itself, since that pointer is all that is needed for insertion, deletion, or access to the rest of the deque.
The loop macro, EACH_DQ, 1oops until the pointer reaches the master node. A third argument is necessary to specify the type of each node:
Here is the full deque.h header:
A natural example of a circular list is provided by train cars on a circular track. To be specific, consider an airport with four terminals (A, B, C, and D, naturally). An automated system of train cars circulates among the four terminals. Each car remains at each terminal for a small random period of time, and then proceeds on its way. When braking, each car's velocity decreases by one meter per second; when accelerating, velocity increases by one meter per second. A car's stopping distance, then, is a simple function of its velocity:
(In other words, stop_dist is the sum from 0 to v of v.) A car begins braking whenever the distance to the next station or to the car ahead (whichever is closer) is less than or equal to a conservative stopping distance, based on current velocity plus one. When not at rest in the station, each car is either accelerating or braking.
The station is four cars long, to accommodate this vastly oversimple algorithm; the patrons do not seem to mind that cars tend to jerk viciously, both in the station and on the track. And in any event, the track is 1000 meters long, but the display resolution is only 100 positions, so the car appears to stand still in the station. The track layout of the airport is, by a remarkable coincidence, the exact layout that was provided by the plot_trk function in Section 5.5:
The question of interest is, what is the number of cars which provides the greatest number of station stops per hour?
The program models the cars as nodes on a deque. (The "car" structure is a CAR.) The car just ahead of car p is located via
This is the program:
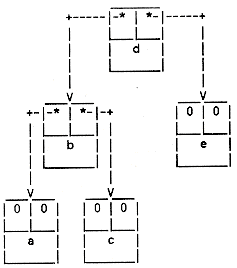
A binary tree is a data structure consisting of branch nodes which contain pointers to sub-trees, and leaf nodes which do not point to other nodes. In the diagram below, there are two branch nodes (b and d), and three leaf nodes (a c, and e).
The top node is known as the root node. A node immediately below a branch node is known as its child; the branch immediately above a node is its parent.
Referring to the small diagram above, if the node names can be taken as indicative of some ordering of the data, then this tree illustrates the use of a tree for storing data in ordered sequence. Every node in a left subtree compares low to the branch above it, and every node in a right subtree compares high.
One common implementation of trees in C uses two pointers in each node to access the left and right subtrees. In the leaf nodes, the pointers are null. The illustration above might look like this in C structures:
According to the packaging conventions of this chapter, we define a TR_NODE ("tree node") like this:
In the simplest representation, each tree is accessed through a single root pointer. In this simple form, "opening a tree" consists of assigning NULL to its root pointer:
Now we can define the properties of the (binary) tree pointed to by pt:
0. If pt is NULL, the tree is empty, i.e., has no nodes.
N. Otherwise, the node *pt is the root node of the tree. The pointers pt->right and pt->left point to trees which are called the subtrees of the node *pt. None of the right and left pointers within either subtree of the root node point back to the root node (i.e., there are no "cycles").
Notice that, unlike the other data structures of this chapter, the tree has a recursive definition. The tree consists of its root node and the two (possibly empty) subtrees. And what does a (non-empty) subtree consist of? Its root node and more subtrees of its own.
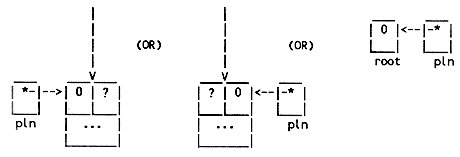
As with our other data structures, we will assume that each node being installed in a tree has been allocated unique storage by the calling function, and that we will simply splice its existing storage into the structure of the tree. The simplest (and often the only) place to install a node is as a leaf, either as the left subtree of an existing leaf, or as the right subtree of an existing leaf, or as the first node to be installed in the tree. In all three cases, some pointer which is initially null will be assigned the address of the node being installed; this initially-null pointer is the link-in of the new node. Thus, to accomplish the insertion we need a pointer to a pointer to tree nodes ("pointer to link-in of node"):
To get ready for the insertion, pln must be caused to point to the pointer which should receive the address of the new node. Here are the three cases:
Once pln points to the proper insertion point, and the node to be inserted is pointed to by some pointer d, say, the actual insertion is accomplished by
after which the node pointed to by d has become a leaf of the tree.
After the insertion, the new node is part of the tree, and there is some link-in pointer -- some node's left pointer, some right pointer, or the root pointer itself -- which points to the new node. The link-in is that unique pointer by which the node is made part of the tree, and it will play an important part in the algorithms to follow.
Trees are often processed by recursive algorithms, because their structure naturally lends itself to recursion. For example, given a pointer cmpfn to an ordering function, the tr_insert function involves a simple recursion:
Searching a tree for a match to a specified key is equally simple, in this recursive form.
The recursion can take a lot of stack space and CPU time, so we will look at an equivalent iterative version:
A similar function can locate the link-in to the parent of a specified node in the tree:
Notice that tr_lfind and tr_lpfind return the link-in, not a pointer to the found node itself. The link-in is more generally useful; for example, it will allow us to detach a node without tracing down from the root.
The tr_detach function has entirely detached a single node or a whole subtree and handed its address back to the calling function. It is no longer part of the tree, and when the calling function is finished with it, its storage must be freed in some fashion. One easy way is to use a function:
Assuming that the tree has been built in some ordered sequence, the "first" node in the tree (the one that compares lowest in the ordering sequence) is the "left-most" node in the tree, i.e., the node that is found by following the left subtree pointers:
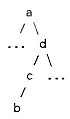
One of the trickiest operations on a sorted tree is to find the successor of a given node, i.e., the node which follows it in sorted sequence. There are several cases. If the node has a right subtree, the successor is the "first" node in the right subtree. The successor of a is b, in this diagram:
If the node has no right subtree, and the node is the left subnode of its parent, then its successor is its parent node. (In the diagram, the successor of c is d.)
Finally, if neither of the above cases applies, the node has no successor; it is the last node in the tree.
We can use TR_LFIRST and TR_LNEXT to construct an EACH_TR macro:
(The tr_lnext function is rather slow for this purpose. See the exercises below for suggestions for faster methods.)
The final operation that we consider is the deletion of a node in an ordered tree. Simply detaching the node is insufficient; we must be sure that the remaining tree is still ordered. In all cases, we assume that we have a pointer, pln, to the link-in of the node to be deleted, possibly provided by tr_lfind. Three cases must be considered. (1) If the node being deleted is a leaf, we simply detach it which sets its link-in to NULL. The detached node, having no children, is then freed. The deletion of b fits this case:
(2) If the node has only one child, we will set the node's link-in to point to the child node, and then free the node itself, as shown by the deletion of c:
(3) If the node has two children, we need to locate its successor. As we saw earlier, since the node has a right subtree, its successor is the "left most" node in that right subtree. Therefore, the successor itself cannot have a left subtree, so the successor's place can be taken by its right subnode, and the successor itself moved into the place of the deleted node. After all this, the node can be freed. This is how a would be deleted:
Expressed in C, here is what it looks like:
The tree.h header summarizes the tree functions from this section:
Exercise 7-1. If a revised version of tr_lfirst and tr_lnext cooperated to create a traversal stack, the time to perform EACH_TR could be drastically reduced. Define a "visit state" for each node: 1 means its left subtree is being visited, 2 means that the node itself is being visited, 3 means that the right subtree is being visited. Here are the five states of the traversal stack while traversing the following tree:
We now have all the functions that we would need to maintain an in-memory "database" of PARTS records, suitable for use with the "parts menu" program from the previous chapter.
p = calloc(N, M);
struct x *px;
px = (struct x *)malloc(sizeof(struct x));
free(px);
free(px);
px = NULL;
p = malloc(N);
p = NULL;
7.2 Singly-linked Lists
#define ST_NODE struct st_node
ST_NODEtypedef struct st_node
{ {ST_NODE *next; struct st_node *next;
char data[4]; char data[4];
}; } ST_NODE;
ST_NODE *head;
head = NULL;
#define ST_OPEN(headp) (*(headp) = NULL)
ST_OPEN(&head);
st_push:
/* st_push - install ST_ NODE at head of stack */
#include "stack.h"
void st_push(headp, p)
ST_NODE **headp;
ST_NODE *p;
{p->next = *headp; /* p->next now points to previous head (or is NULL) */
*headp = p; /* *headp now points to p */
}
st_pop:
/* st_pop - detach top node of stack and return pointer to it */
#include "stack.h"
ST_NODE *st_pop(headp)
ST_NODE **headp;
{ST_NODE *p;
if (*headp == NULL)
return (NULL);
p = *headp; /* p points to top of stack */
*headp = p->next; /* headp now points to next node (or is NULL) */
p->next = NULL; /* prevent dangling ptr */
return (p);
}
st_close:
/* st_close - close the stack accessed via *headp */
# include "stack.h"
void st_close(headp)
ST_NODE **headp;
{ST_NODE *p;
ST_NODE *pnext;
for (p = *headp; p != NULL; p = pnext)
{pnext = p->next;
free(p); /* p is (momentarily) undefined */
}
*headp = NULL; /* prevent dangling ptr */
}
for (p = head; p != NULL; p = p->next)
process *p
#define EACH_ST(head, p) for ((p) = (head); (p) != NULL; (p) = (p)->next)
EACH_ST(head, p)
process *p
#define ST_IS_EMPTY(head) ((head) == NULL)
#define ST_FIRST(head) (head)
#define ST_NEXT(p) ((p)->next)
#define ST_NODE struct st_node
ST_NODE
{ST_NODE *next;
/* ... */
};
#define NAME_NODE struct name_node
NAME_NODE
{NAME_NODE *next;
char data[4];
};
NAME_NODE *name_head = NULL;
NAME_NODE *p = NULL;
pointer.h:
/* pointer.h - concise macros for pointer checking and casting */
/* PNN(p) - test that p is not NULL, return p */
/* PNNC(p, t) - test that p is not NULL, return p cast to type t */
#ifndef POINTER_H
#define POINTER_H
#ifndef NDEBUG
#define PNN(p) ((p) != NULL ? (p) : PNN_BAD(p))
#define PNNC(p, t) ((p) != NULL ? (t)(p) : (t)PNN_BAD(p))
#define PNN_BAD(p) (fprintf(stderr, "NULL\n"), p)
#else
#define PNN(p) (p)
#define PNNC(p,t) ((t)(p))
#endif
#endif
stack.h:
/* stack.h - header for stack package */
#ifndef STACK_H
#define STACK_H
#include "local.h"
#include "pointer.h"
#define ST_NODE struct st_node
ST_NODE
{ST_NODE *next;
/* ... */
};
void st_close(); /* PARMS(ST_NODE **headp) */
ST_NODE *st_pop(); /* PARMS(ST_NODE **headp) */
void st_push(); /* PARMS(ST_NODE **headp, ST_NODE *p) */
#define ST_P(p) PNNC(p, ST_NODE *)
#define ST_PP(p) PNNC(p, ST_NODE **)
#define ST_CLOSE(h) (st_close(ST_PP(h)))
#define ST_POP(h) (st_pop(ST_PP(h)))
#define ST_PUSH(h, p) (st_push(ST_PP(h), ST_P(p)))
#define EACH_ST(head, p) for ((p) = (head); (p) != NULL; (p) = (p)->next)
#define ST_FIRST(head) (head)
#define ST_IS_EMPTY(head) ((head) == NULL)
#define ST_OPEN(headp) (*(headp) = NULL)
#define ST_NEXT(p) ((p)->next)
#endif
st_main.c:
/* st_main - test routine for stack package
*/
#include "local.h"
#include "stack.h"
#define NAME_NODE struct name_node
NAME_NODE
{NAME_NODE *next;
char data[4];
};
NAME_NODE *head = NULL; /* head node of stack */
NAME_NODE *p = NULL; /* current node */
void show_cmds(), push_name(), pop_name(), dump_names();
/* st_main (main) */
main()
{char buf[2]; /* buffer for input */
ST_OPEN(&head); /* open the stack */
show_cmds();
while (getreply("?: ", buf, 2) != EOF){switch (buf[0])
{case '+' :
push_name();
break;
case '-':
pop_name();
break;
case '=':
dump_names();
break;
case '0':
ST_CLOSE(&head);
ST_OPEN(&head); /* open the stack again */
break;
case '?':
show_cmds();
break;
default:
printf("unknown command: %c\n", buf[0]);show_cmds();
break;
}
}
exit(SUCCEED);
}
/* show_cmds -- show legal commands */
void show_cmds()
{printf("Type + to push, - to pop, = to print, 0 to reset:\n");}
/* push_name - push new name on stack */
void push_name()
{p = (NAME_NODE *)malloc(sizeof(NAME_NODE));
if (p == NULL)
error("out of space", "");if (getreply("name: ", p->data, 4) == EOF)error("unexpected EOF", "");ST_PUSH(&head, p);
}
/* pop_name - pop a name off stack */
void pop_name()
{p = (NAME_NODE *)ST_POP(&head);
if (p == NULL)
printf("EMPTY STACK\n");else
{printf("name= %s\n", p->data);free(p);
}
}
/* dump_names - print the current stack of names */
void dump_names()
{if (ST_IS_EMPTY(head))
printf("EMPTY STACK\n");else
EACH_ST(head, p)
printf("name= %s\n", p->data);}
7.3 Queues
#define Q_OPEN(frontp, rearp) (*(frontp) = *(rearp) = NULL)
#define Q_FIRST (front) (front)
define Q_NEXT(p) ((p)->next)
q_pop:
/* q_pop - detach front node of queue and return pointer to it */
#include "queue.h"
Q_NODE *q_pop(frontp, rearp)
Q_NODE **frontp, **rearp;
{Q_NODE *p;
if (*frontp == NULL)
return (NULL);
p = *frontp; /* p points to front of queue */
*frontp = Q_NEXT(p); /* front now points to next node (or NULL) */
if (*frontp == NULL) /* if queue is now empty, */
*rearp = NULL; /* then make both ptrs NULL */
Q_NEXT(p) = NULL; /* prevent dangling ptr */
return (p);
}
q_r_detach:
/* q_r detach - detach queue node that *pp links-in and return pointer to it */
#include "queue.h"
Q_NODE *q_r_detach(frontp, rearp, pp)
Q_NODE **frontp, **rearp;
Q_NODE **pp;
{Q_NODE *p2; /* ptr to detached node */
if (*pp == NULL)
return (NULL);
p2 = *pp; /* p2 points to node to detach */
*pp = Q_NEXT(p2); /* *pp now points to next node (or NULL) */
if (*frontp == NULL) /* if queue is now empty, */
*rearp = NULL; /* then make both ptrs NULL */
Q_NEXT(p2) = NULL; /* prevent dangling ptr */
return (p2);
}
q_push:
/* q_push - install Q_NODE at front of queue */
#include "queue.h"
void q_push(frontp, rearp, p)
Q_NODE **frontp, **rearp;
Q_NODE *p;
{Q_NEXT(p) = *frontp; /* p points to previous front (or NULL) */
*frontp = p; /* *frontp now points to p */
if (*rearp == NULL) /* if queue was empty, */
*rearp = p; /* *rearp also points to p */
}
q_r_insert:
/* q_r_insert - install Q_NODE after *pp */
#include "queue.h"
void q_r_insert(frontp, rearp, p, pp)
Q_NODE **frontp, **rearp;
Q_NODE *p;
Q_NODE **pp;
{Q_NEXT(p) = *pp; /* p points to node following *pp (or NULL) */
*pp = p; /* *pp now points to p */
if (*rearp == NULL) /* if queue was empty, */
*rearp = p; /* *rearp also points to p */
}
q_append:
/* q_append - install Q_NODE at rear of queue */
#include "queue.h"
void q_append(frontp, rearp, p)
Q_NODE **frontp, **rearp;
Q_NODE *p;
{Q_NEXT(p) = NULL; /* new node will be rear of queue */
if (*frontp == NULL) /* if queue was empty, */
*frontp = *rearp = p; /* p becomes front and rear */
else
{Q_NEXT(*rearp) = p; /* splice p into queue */
*rearp = p; /* p becomes rear of queue */
}
}
q_close:
/* q_close - close the queue accessed via *frontp and *rearp */
#include "queue.h"
void q_close(frontp, rearp)
Q_NODE **frontp, **rearp;
{Q_NODE *p;
Q_NODE *pnext;
for (p = *frontp; p != NULL; p = pnext)
{pnext = Q_NEXT(p);
free(p); /* p is (momentarily) undefined */
}
*frontp = *rearp = NULL; /* prevent dangling ptr */
}
#define EACH_Q(front, p) for ((p) = front; (p) != NULL; (p) = (p)->next)
#define Q_IS_EMPTY(front) ((front) == NULL)
q_insert:
/* q_insert - install Q_NODE at proper place in queue */
#include "queue.h"
void q_insert(frontp, rearp, p, cmpfn)
Q_NODE **frontp, **rearp;
Q_NODE *p;
int (*cmpfn)(); /* function for comparisons */
{Q_NODE *p2;
if (*frontp == NULL /* if queue was empty, */
|| (*cmpfn)(p, *frontp) < 0) /* or if p comes first, */
Q_PUSH(frontp, rearp, p); /* push p onto front */
else
{for (p2 = *frontp; ; p2 = Q_NEXT(p2))
{if (Q_NEXT(p2) == NULL)
{ /* if end of queue, */Q_APPEND(frontp, rearp, p); /* append p at rear of queue */
break;
}
else if ((*cmpfn)(p, Q_NEXT(p2)) < 0)
{ /* if p sorts before Q_NEXT(p2) */Q_R_INSERT(frontp, rearp, p, p2); /* insert after p2 */
break;
}
}
}
}
q_lfind:
/* q_lfind - search queue for equal match to p, return its link-in
* Return NULL if no match
*/
#include "queue.h"
Q_NODE **q_lfind(frontp, rearp, p, cmpfn)
Q_NODE **frontp, **rearp;
Q_NODE *p;
int (*cmpfn)();
{Q_NODE **pp;
for (pp = frontp; *pp != NULL; pp = &Q_NEXT(*pp))
if ((*cmpfn)(*pp, p) == 0)
return (pp);
return (NULL);
}
queue.h:
/* queue.h - header for queue package */
#ifndef QUEUE_H
#define QUEUE_H
#include "local.h"
#include "pointer.h"
#define Q_NODE struct q_node
Q_NODE
{Q_NODE *next;
/* ... */
};
void q_append(); /* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE *p) */
void q_close(); /* PARMS(Q_NODE **frontp, Q_NODE **rearp) */
void q_insert();
/* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE *p, int (*cmpfn)()) */
Q_NODE **q_lfind();
/* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE *p, int (*cmpfn)()) */
Q_NODE *q_pop(); /* PARMS(Q_NODE **frontp, Q_NODE **rearp) */
void q_push(); /* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE *p) */
Q_NODE *q_r_detach();
/* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE **pp) */
void q_r_insert();
/* PARMS(Q_NODE **frontp, Q_NODE **rearp, Q_NODE *p, Q_NODE **pp) */
/* (more)
*/
#define Q_PP(p) PNNC(p, Q_NODE **)
#define Q_P(p) PNNC(p, Q_NODE *)
#define Q_APPEND(fp, rp, p) q_append(Q_PP(fp), Q_PP(rp), Q_P(p))
#define Q_CLOSE(fp, rp) q_close(Q_PP(fp), Q_PP(rp))
#define Q_INSERT(fp, rp, p, fn) q_insert(Q_PP(fp), Q_PP(rp), Q_P(p), fn)
#define Q_LFIND(fp, rp, p, fn) q_lfind(Q_PP(fp), Q_PP(rp), Q_P(p), fn)
#define Q_POP(fp, rp) q_pop(Q_PP(fp), Q_PP(rp))
#define Q_PUSH(fp, rp, p) q_push(Q_PP(fp), Q_PP(rp), Q_P(p))
#define Q_R_DETACH(fp, rp, pp) q_r_detach(Q_PP(fp), Q_PP(rp), Q_PP(pp))
#define Q_R_INSERT(fp, rp, p, pp) q_r_insert(Q_PP(fp), Q_PP(rp), Q_P(p), Q_PP(pp
#define Q_IS EMPTY(front) ((front) == NULL)
#define Q_OPEN(frontp, rearp) (*(frontp) = *(rearp) = NULL)
#define Q_NEXT(p) ((p)->next)
#define EACH_Q(front, p) for ((p) = front; (p) != NULL; p = (p)->next)
#endif
task.h:
/* task.h - header for task package */
#ifndef TASK_H
#define TASK_H
#include "local.h"
#include "queue.h"
typedef short TIME;
#define TASK struct task
TASK
{TASK *next;
TIME start;
char desc[40];
};
#endif
t_main.c:
/* t_main - manage a queue of tasks */
#include "local.h"
#include "queue.h"
#include "task.h"
TASK *front = NULL; /* front node of queue */
TASK *rear = NULL; /* rear node of queue */
TASK *p = NULL; /* current node */
void insert_task(), pop_task(), dump_tasks(), show_cmds();
main()
{char buf[2]; /* buffer for input */
show_cmds();
Q_OPEN(&front, &rear); /* open the queue */
while (getreply("?: ", buf, 2) != EOF){switch (buf[0])
{case '>':
insert_task();
break;
case '-':
pop_task();
break;
case '=':
dump_tasks();
break;
case '0':
Q_CLOSE(&front, &rear);
Q_OPEN(&front, &rear); /* open the queue */
break;
default:
printf("unknown command: %c\n", buf[0]);show_cmds();
break;
}
}
exit(SUCCEED);
}
/* show_cmds -- show legal commands */
void show_cmds()
{printf("Type > to insert, - to pop, = to print, 0 to reset:\n");}
/* cmptime - compare the start members of two TASKS */
int cmptime(t1, t2)
TASK *t1, *t2;
{if (t1->start < t2->start)
return (-1);
else if (t1->start == t2->start)
return (0);
else
return (1);
}
/* insert_task - insert new name on queue */
void insert_task()
{char sstart[5];
p = (TASK *)malloc(sizeof(TASK));
if (p == NULL)
error("out of space", "");if (getreply("start: ", sstart, sizeof(sstart)) == EOF)error("unexpected EOF", "");p->start = atoi(sstart);
if (getreply("desc: ", p->desc, sizeof(p->desc)) == EOF)error("unexpected EOF", "");Q_INSERT(&front, &rear, p, cmptime);
}
/* pop task - pop a name off queue */
void pop_task()
{p = (TASK *)Q_POP(&front, &rear);
if (p == NULL)
printf("EMPTY QUEUE\n");else
{printf("start=%5d desc=%s\n", p->start, p->desc);free(p);
}
}
/* dump_tasks - print the current queue of names */
void dump_tasks()
{if (front == NULL)
printf("EMPTY QUEUE\n");else
EACH_Q(front, p)
printf("start=%5d desc=%s\n", p->start, p->desc);}
7.4 Deques: Double-Ended Queues
#define DQ_NODE struct dq_node
DQ_NODE
{DQ_NODE *left;
DQ_NODE *right;
/* ... */
};
dq_open:
/* dq_open - open a deque */
#include "deque.h"
void dq_open(pdq)
DQ_NODE **pdq;
{*pdq = (DQ_NODE *)malloc(sizeof(DQ_NODE));
if (*pdq == NULL)
return;
(*pdq)->left = (*pdq)->right = (*pdq);
}
dq_close:
/* dq_close - close a deque */
#include "deque.h"
void dq_close(pdq)
DQ_NODE **pdq; /* ptr to ptr to master DQ_NODE */
{DQ_NODE *p;
DQ_NODE *pnext;
for (p = (*pdq)->right; p != (*pdq); p = pnext)
{pnext = p->right;
free(p);
}
free(*pdq);
*pdq = NULL;
}
#define DQ_PRED(dq, d) \
(DQ_P(d)->left == PNN(dq) ? (dq->left) : (DQ_P(d)->left))
#define DQ_SUCC(dq, d) \
(DQ_P(d)->right == PNN(dq) ? (dq->right) : (DQ_P(d)->right))
dq_detach:
/* dq_detach - detach node d from deque */
#include "deque.h"
DQ_NODE *dq_detach(dq, d)
DQ_NODE *dq;
DQ_NODE *d;
{DQ_NODE *p;
DQ_NOOE *q;
if (d == dq)
return (NULL);
q = d->right;
p = d->left;
p->right = q;
q->left = p;
return (d);
}
dq_r_insert:
/* dq_r_insert - insert node d to the right of node p */
#include "deque.h"
void dq_r_insert(d, p)
DQ_NODE *d;
DQ_NODE *p;
{DQ_NODE *q;
q = p->right;
d->left = p;
d->right = q;
p->right = d;
q->left = d;
}
#define DQ_P(p) PNNC(p, DQ_NODE *) /* non-NULL, cast to DQ_NODE * */
#define DQ_R_INSERT(d, p) dq_r_insert(DQ_P(d), DQ_P(p))
#define DQ_L_INSERT(d, p) DQ_R_INSERT((d), (p)->left)
#define DQ_PUSH(dq, d) DQ_R_INSERT((d), (dq))
dq_pop:
/* dq_pop - remove leftmost node and return pointer to it
* Treats deque as a stack to the right of dq master node.
*/
#include "deque.h"
DQ_NODE *dq_pop(dq)
DQ_NODE *dq;
{DQ_NODE *d;
d = dq->right;
if (d == dq)
return (NULL);
return (DQ_DETACH(dq, d));
}
#define DQ_APPEND(dq, d) DQ_R_INSERT(d, (dq)->left)
#define DQ_IS_EMPTY(dq) (PNN(dq)->right == PNN(dq))
dq_insert:
/* dq_insert - install DQ_NODE at proper place in deque */
#include "deque.h"
void dq_insert(dq, p, cmpfn)
DQ_NODE *dq;
DQ_NODE *p;
int (*cmpfn)( ) /* function for comparisons: neg, zero, or pos */
{DQ_NODE *p2;
if (DQ_IS_EMPTY(dq) /* if deque was empty, */
|| (*cmpfn)(p, DQ_FIRST(dq)) < 0) /* or if p comes first, */
DQ_PUSH(dq, p); /* push p onto front */
else /* else, p must sort after p2 */
{EACH_DQ(dq, p2, DQ_NODE) /* find where p belongs */
{if (p2->right == dq)
{ /* if end of deque, */DQ_APPEND(dq, p); /* append p at rear of deque */
break;
}
else if ((*cmpfn)(p, p2->right) < 0)
{ /* if p sorts before p2->right */DQ_R_INSERT(p, p2); /* insert after p2 */
break;
}
}
}
}
dq_find:
/* dq_find - search deque for equal match to d, return ptr to match
* Return NULL if no match
*/
#include "deque.h"
DQ_NODE *dq_find(dq, d, cmpfn)
DQ_NODE *dq;
DQ_NODE *d;
int (*cmpfn)( ); /*function for comparisons */
{DQ_NODE *d2;
EACH_DQ(dq, d2, DQ_NODE)
if ((*cmpfn)(d2, d) == 0)
return (d2);
return (NULL);
}
dq_first:
/* dq_first - produce ptr to first deque node, otherwise NULL */
#include "deque.h"
DQ_NODE *dq_first(dq)
DQ_NODE *dq;
{if (dq->right == dq)
return (NULL);
return (dq->right);
}
#define EACH_DQ(dq, d, t) \
for (d = (t *)(dq)->right; (DQ_NODE *)(d) != dq; d = (d)->right)
deque.h:
/* deque.h - header for deque package */
#ifndef DEQUE_H
#define DEQUE_H
#include "local.h"
#include "pointer.h"
#define DQ_NODE struct dq_node
DQ_NODE
{DQ_NODE *left;
DQ_NODE *right;
/* ... */
};
#define DQ_P(p) PNNC(p, DQ_NODE *)
#define DQ_PP(p) PNNC(p, DQ_NODE **)
void dq_close( ); /* PARMS(DQ_NODE **pdq) */
DQ_NODE *dq_detach( ); /* PARMS(DQ_NODE *dq, DQ_NODE *d) */
DQ_NODE *dq_find( ); /* PARMS(DQ_NODE *dq, DQ_NODE *d, int (*cmpfn)( )) */
void dq_insert( ); /* PARMS(DQ_NODE *dq, DQ_NODE *d, int (*cmpfn)( )) */
void dq_open( ); /* PARMS(DQ_NODE **pdq) */
DQ_NODE *dq_pop( ); /* PARMS(DQ_NODE *dq) */
void dq_r_insert( ); /* PARMS(DQ_NODE *d, DQ_NODE *p) */
/* (more) */
/* pure macros */
#define DQ_APPEND(dq, d) DQ_R_INSERT(d, (dq)->left)
#define DQ_IS_EMPTY(dq) (PNN(dq)->right == PNN(dq))
#define DQ_L_DETACH(dq, d) DQ_DETACH(dq, (d)->left)
#define DQ_L_INSERT(d, p) DQ_R_INSERT((d), (p)->left)
#define DQ_PRED(dq, d) \
(DQ_P(d)->left == PNN(dq) ? (dq->left) : (DQ_P(d)->left))
#define DQ_PUSH(dq, d) DQ_R_INSERT((d), (dq))
#define DQ_R_DETACH(dq, d) DQ_DETACH(dq, (d)->right)
#define DQ_SUCC(dq, d) \
(DQ_P(d)->right == PNN(dq) ? (dq->right) : (DQ_P(d)->right))
#define EACH_DQ(dq, d, t) \
for (d = (t *)(dq)->right; (DQ_NODE *)(d) != dq; d = (d)->right)
/* function-interface macros */
#define DQ_CLOSE(pdq) dq_close(PNN(pdq))
#define DQ_DETACH(dq, d) dq_detach(DQ_P(dq), DQ_P(d))
#define DQ_FIND(dq, d, fn) dq_find(PNN(dq), DQ_P(d), fn)
#define DQ_FIRST(dq) dq_first(PNN(dq))
#define DQ_INSERT(dq, d, fn) dq_insert(PNN(dq), DQ_P(d), fn)
#define DQ_OPEN(pdq) dq_open(PNN(pdq))
#define DQ_POP(dq) dq_pop(PNN(dq))
#define DQ_R_INSERT(d, p) dq_r_insert(DQ_P(d), DQ_P(p))
#endif
stop_dist(0)== 0
stop_dist(v) == v + stop_dist(v-1)
psucc = (CAR *)DQ_SUCC(p);
run_cars.c:
/* run_cars - simulate airport terminal train cars */
#include "deque.h"
#include "screen.h"
#define TRKSIZE 1000
#define CAR struct car
CAR
{CAR *left; /* pointer to previous deque node; !NULL */
CAR *right; /* pointer to next deque node; !NULL */
short pos; /* position on track; {0:TRKSIZE-1} */short vel; /* velocity; {0:SHORT_MAX} */char ident[2]; /* identifier for this car; {"a":"z":} */};
void init(); /* initialize the simulation */
void run(); /* run one time step */
DQ_NODE *cars = NULL; /* pointer to master deque node */
CAR *p = NULL; /* pointer to a CAR */
short ncars = 0; /* number of cars on track; {2:26} */char idents[] = "abcdefghijklmnopqrstuvwxyz";
main(ac, av)
int ac;
char *av[];
{short t; /* loop counter */
SCR_CMDCHAR c; /* input from keyboard */
if (ac < 2)
error("usage: run_cars #-of-cars", "");ncars = atoi(av[1]);
if (ncars < 2 || ncars > 26)
error("#-of-cars must be between 2 and 26", "");scr_open();
scr_clear();
scr_curs(21, 40); scr_putc('A');scr_curs(11, 75); scr_putc('B');scr_curs( 1, 40); scr_putc('C');scr_curs(11, 5); scr_putc('D');init();
do {for (t = 0; t < 200; ++t)
run();
scr_curs(scr_lins - 1, 0);
scr_print("More? ");scr_refresh();
c = scr_getkey();
scr_putc(c);
} while (c == 'y');
scr_close();
exit(SUCCEED);
}
/* init - initialize the simulation */
void init()
{short i; /* loop counter; (0:ncars-1} */
DQ_OPEN(&cars);
for (i = 0; i < ncars; ++i)
{p = (CAR *)malloc(sizeof(CAR));
if (p == NULL)
error("out of space", "");p->pos = i * (TRKSIZE / ncars);
p->vel = 0;
p->ident[0] = idents[i];
p->ident[1] = '\0';
DQ_APPEND(cars, p);
}
}
/* run - run the simulation for one time step */
void run()
{short to_station; /* distance to next station */
short to_car; /* distance to next car */
short to_stop; /* safe distance required to stop this car */
short i; /* loop counter */
CAR *psucc; /* ptr to successor of car p */
EACH_DQ(cars, p, CAR)
{plot_trk(p->pos / (TRKSIZE/100), ' ');
p->pos = IMOD(p->pos + p->vel, TRKSIZE);
plot_trk(p->pos / (TRKSIZE/100), p->ident[0]);
to_station = IMOD(p->pos, TRKSIZE / 4);
psucc = (CAR *)DQ_SUCC(cars, p);
to_car = IMOD(psucc->pos - p->pos, TRKSIZE);
for (i = 1, to_stop = 0; i <= p->vel+1; ++i)
to_stop += i;
if (to_car < 10)
p->vel = 0; /* screeching halt */
else if (to_station <= 5)
p->vel = rand() & 0x1; /* random jerk in station */
else if (MIN(to_station, to_car) < to_stop && p->vel > 0)
--p->vel; /* slow down */
else
++p->vel; /* speed up */
}
scr_refresh();
}
7.5 Trees
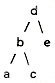
#define TR_NODE struct tr_node
TR_NODE
{TR_NODE *right;
TR_NODE *left;
/* ... */
};
#define TR_OPEN(ppt) (*(ppt) = NULL)
TR_NODE **pln;
*pln = d;
tr_insert:
/* tr_insert - insert a single node in tree (recursive version) */
#include "tree.h"
void tr_insert(plt, pn, cmpfn)
TR_NODE **plt; /* ptr to link-in of tree or subtree */
TR_NODE *pn; /* ptr to node to be inserted */
int (*cmpfn)( ); /* ptr to comparison function */
{TR_NODE *pt; /* ptr to tree (or subtree) */
int cmp; /* result of key comparison; neg, zero, or pos */
pt = *plt; /* pt now pts to current tree (if any) */
if (pt == NULL) /* if plt pointed to a null pointer, */
{pn->left = pn->right = NULL;. /* has no sub trees yet */
*plt = pn; /* then this is the place to install pn; do so */
}
else if ((cmp = (*cmpfn)(pn, pt)) == 0) /* if already in tree, */
return; /* then don't install */
else if (cmp < 0) /* if node's key compares low */
TR_INSERT(&pt->left, pn, cmpfn); /* then insert in left tree */
else /* otherwise, */
TR_INSERT(&pt->right, pn, cmpfn); /* insert in right tree */
}
tr_lfind(#1):
/* tr_lfind - find node matching a specified key
* recursive version
* never returns NULL
*/
#include "tree.h"
TR_NODE **tr_lfind(plt, pn, cmpfn)
TR_NODE **plt; /* ptr to link-in of tree or subtree */
TR_NODE *pn; /* ptr to structure containing key to match */
int (*cmpfn)( ); /* ptr to comparison function */
{TR_NODE *pt; /* ptr to current tree */
int cmp; /* comparison result: neg, zero, pos */
pt = *plt; /* pt now points to current tree */
if (pt == NULL) /* if plt points to a null pointer, */
return (plt); /* the data isn't in the tree */
else if ((cmp = (*cmpfn)(pn, pt)) == 0) /* if key already in tree, */
return (plt); /* return its node's link-in */
else if (cmp < 0) /* if key compares low, */
return (TR_LFIND(&pt->left, pn, cmpfn)); /* search in left tree */
else /* otherwise, /*
return (TR_LFIND(&pt->right, pn, cmpfn)); /* search in right tree /*
}
tr_lfind(#2):
/* tr_lfind - find node matching a specified key
* iterative version
* never returns NULL
*/
#include "tree.h"
TR_NODE **tr_lfind(plt, pn, cmpfn)
TR NODE **plt; /* ptr to link-in of tree or subtree */
TR_NODE *pn; /* ptr to structure containing key to match */
int (*cmpfn)( ); /* ptr to comparison function */
{TR_NODE *pt; /* ptr to current tree */
int cmp; /* comparison result: neg, zero, pos */
FOREVER
{pt = *plt; /* pt now points to current tree */
if (pt == NULL) /* if plt points to a null pointer, */
return (plt); /* the data isn't in the tree */
else if ((cmp = (*cmpfn)(pn, pt)) == 0) /* if key already in tree, */
return (plt); /* return its node's link-in */
else if (cmp < 0) /* if key compares low, */
plt = &pt->left; /* then search in left tree */
else /* otherwise, */
plt = &pt->right; /* search in right tree */
}
}
tr_lpfind:
/* tr_lpfind - find parent of node matching a specified key
* iterative version
* never returns NULL; may return addr of null ptr
*/
#include "tree.h"
static TR_NODE *nullp = NULL; /* used to return addr of null ptr */
TR NODE **tr_lpfind(plt, pn, cmpfn)
TR NODE **plt; /* ptr to link-in of tree or subtree */
TR_NODE *pn; /* ptr to structure containing key to match */
int (*cmpfn)(); /* ptr to comparison function */
{TR_NODE *pt; /* ptr to current tree */
TR_NODE **plp; /* ptr to link-in of parent of tree */
int cmp; /* comparison result: neg, zero, pos */
plp = &nullp; /* root has no parent */
FOREVER
{pt = *plt; /* pt now points to current tree */
if (pt == NULL) /* if plt points to a null pointer, */
return (&nullp); /* the data isn't in the tree */
else if ((cmp = (*cmpfn)(pn, pt)) == 0) /* if key already in tree, */
return (plp); /* return its parent's link-in */
plp = plt; /* before starting subtree, save plt */
if (cmp < 0) /* if key compares low, */
plt = &pt->left; /* then search in left tree */
else /* otherwise, */
plt = &pt->right; /* search in right tree */
}
}
tr_detach:
/* tr_detach - detach node (or subtree) from tree, given link-in
*/
#include "tree.h"
TR_NODE *tr_detach(pln)
TR_NODE **pln; /* ptr to link-in of node to be detached */
{TR_NODE *p;
p = *pln; /* hold the address of the node */
*pln = NULL; /* detach the node */
return (p); /* return its address */
}
tr_close:
/* tr_close - free a tree or subtree */
#include "tree.h"
void tr_close(plt)
TR_NODE **plt; /* ptr to link-in of tree */
{TR_NODE *pt; /* ptr to root of tree */
pt = *plt; /* pt now points to root of tree */
if (pt == NULL) /* if link-in is NULL, */
return; /* nothing to do, so return */
TR_CLOSE(&pt->left); /* free left subtree */
TR_CLOSE(&pt->right); /* free right subtree */
free(pt); /* free the node itself */
}
tr_lfirst:
/* tr_lfirst - find first node in tree
* Returned value is ptr to link-in of first node
* never returns NULL, and never points to null ptr
*/
#include "tree.h"
TR_NODE **tr_lfirst(plt)
TR_NODE **plt; /* ptr to (non-null) link-in of tree */
{TR_NODE **pln; /* ptr to link-in of node */
for (pln = plt; (*pln)->left != NULL; pln = &(*pln)->left)
;
return (pln);
}
tr_lnext:
/* tr_lnext - find the successor of node pn
* Returned value is ptr to link-in of successor node
* Never returns NULL; may return addr of a null ptr
*/
#include "tree.h"
static TR_NODE *nullp = NULL; /* used to return addr of null ptr */
TR_NODE **tr_lnext(plt, pn, cmpfn)
TR_NODE **plt; /* ptr to link-in of tree */
TR_NODE *pn; /* ptr to specific node of tree */
int (*cmpfn)( ); /* ptr to comparison function */
{TR_NODE **pls; /* ptr to link-in of successor */
TR_NODE **pln; /* ptr to link-in of a TR_NODE */
if (pn->right != NULL) /* if node has a right subtree, */
{ /* return ptr to link-in of "leftmost" node in right subtree */return (TR_LFIRST(&pn->right));
}
else /* if node has no right subtree, */
{ /* return ptr to link-in of parent of pn */pln = TR_LPFIND(plt, pn, cmpfn);
if (*pln != NULL && (*pln)->left == pn)
return (pln); /* node is left subtree of parent */
else
return (&nullp); /* node is rightmost in tree */
}
}
#define EACH_TR(plt, p, t, fn) \
for (p = (t *)*TR_LFIRST(plt); (p) != NULL; p = (t *)*TR_LNEXT(plt, p, fn))
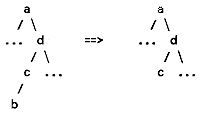

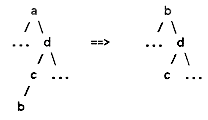
tr_delete:
/* tr_delete - delete the node **pln from tree *plt
*/
#include "tree.h"
void tr_delete(plt, pln, cmpfn)
TR_NODE **plt; /* ptr to link-in of tree */
TR_NODE **pln; /* ptr to link-in of node */
int (*cmpfn)(); /* ptr to comparison function */
{TR_NODE *pn; /* ptr to specific node of tree */
TR_NODE *ps; /* ptr to node's successor */
TR_NODE **pls; /* ptr to link-in of successor */
pn = *pln; /* pn pts to the node to delete */
if (pn->right == NULL) /* if node has no right subtree, */
{if (pn->left == NULL) /* if node has no children, */
*pln = NULL; /* replacement for pn is NULL */
else /* if node has L subtree, but not R, */
*pln = pn->left; /* replacement is pn's L subtree */
}
else if (pn->left == NULL) /* if node has R subtree, but not L */
*pln = pn->right; /* replacement is pn's R subtree */
else /* if node has R and L subtrees *
{pls = TR_LNEXT(plt, pn, cmpfn); /* get ptr to link-in of succ */
ps = *pls; /* ps now points to successor */
*pls = ps->right; /* succ's R subtree takes succ's place */
ps->right = pn->right; /* succ acquires node's R ... */
ps->left = pn->left; /* ... and L subtree */
*pln = ps; /* replacement is successor */
}
free(pn);
}
tree.h:
/* tree.h - header for tree functions
*/
#ifndef TREE_H
#define TREE_H
#include "local.h"
#include "pointer.h"
#define TR_NODE struct tr_node
TR_NODE
{TR_NODE *right;
TR_NODE *left;
/* ... */
};
void tr_close(); /* PARMS(TR_NODE **plt) */
void tr_delete(); /* PARMS(TR_NODE **plt, TR_NODE **pln, int (*cmpfn)()) */
TR_NODE *tr_detach(); /* PARMS(TR_NODE **pln) */
void tr_insert(); /* PARMS(TR_NODE **plt, TR_NODE *pn, int (*cmpfn)()) */
TR_NODE **tr_lfind(); /* PARMS(TR_NODE **plt, TR_NODE *pn, int (*cmpfn)()) */
TR_NODE **tr_lfirst(); /* PARMS(TR_NODE **plt) */
TR_NODE **tr_lpfind(); /* PARMS(TR_NODE **plt, TR_NODE *pn, int (*cmpfn)()) */
TR_NODE **tr_lnext(); /* PARMS(TR_NODE **plt, TR_NODE *pn, int (*cmpfn)()) */
#define TR_RIGHT(p) ((p)->right)
#define TR_LEFT(p) ((p)->left)
#define TR_P(p) PNNC(p, TR_NODE *)
#define TR_PP(p) PNNC(p, TR_NODE **)
#define TR_CLOSE(plt) tr_close(TR_PP(plt))
#define TR_DELETE(plt, pln, fn) tr_delete(TR_PP(plt), TR_PP(pln), fn)
#define TR_DETACH(pln) tr_detach(TR_PP(pln))
#define TR_INSERT(plt, pn, fn) tr_insert(TR_PP(plt), TR_P(pn), fn)
#define TR_LFIND(plt, pn, fn) tr_lfind(TR_PP(plt), TR_P(pn), fn)
#define TR_LFIRST(plt) tr_lfirst(TR_PP(plt))
#define TR_LPFIND(plt, pn, fn) tr_lpfind(TR_PP(plt), TR_P(pn), fn)
#define TR_LNEXT(plt, pn, fn) tr_lnext(TR_PP(plt), TR_P(pn), fn)
/* true macros */
#define TR_OPEN(plt) (*(plt) = NULL)
#define TR_FIRST(plt) (*TR_LFIRST(plt))
#define TR_FIND(plt, pn, fn) (*TR_LFIND(plt, pn, fn))
#define TR_NEXT(plt, pn, fn) (*TR_LNEXT(plt, pn, fn))
#define EACH_TR(plt, p, t, fn) \
for (p = (t *)*TR_LFIRST(plt); (p) != NULL; p = (t *)*TR_LNEXT(plt, p, fn))
#endif
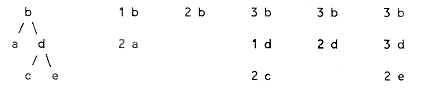
part_db_tr.c:
/* part_db_tr.c - simulated database access to parts
* uses binary tree for in-memory storage
*/
#include "tree.h"
*include "part.h"
#define TPART struct tr_part
TPART
{TPART *right;
TPART *left;
PART part;
};
static TPART tpart = {0};static TPART *parts = NULL;
/* db_cmp_part - comparison function for database access */
static int db_cmp_part(p1, p2)
TPART *p1, *p2;
{return (strcmp(p1->part.part_no, p2->part.part_no));
}
/* (more) */
/* db_add_part - add a part record to database */
bool db_add_part(partp)
PART *partp;
{TPART *p;
p = (TPART *)malloc(sizeof(TPART));
if (p == NULL)
{remark("Part storage is full", "");return (NO);
}
STRUCTASST(p->part, *partp);
TR_INSERT(&parts, p, db_cmp_part);
return (YES);
}
/* db_find_part - find a part record in database */
bool db_find_part(partp)
PART *partp;
{TPART *pn; /* ptr to part record in tree */
STRUCTASST(tpart.part, *partp);
pn = (TPART *)TR_FIND(&parts, &tpart, db_cmp_part);
if (pn == NULL)
return (NO);
STRUCTASST(*partp, pn->part);
return (YES);
}
/* db_del_part - delete a part record in database */
bool db_del_part(partp)
PART *partp;
{TPART **pln; /* ptr to link-in of part record in tree */
STRUCTASST(tpart.part, *partp);
pln = (TPART **)TR_LFIND(&parts, &tpart, db_cmp_part);
if (*pln == NULL)
{remark("No record for this part", "");return (NO);
}
TR_DELETE(&parts, pln, db_cmp_part);
return (YES);
}
/* db_chg_part - change a part record in database */
bool db_chg_part(partp)
PART *partp;
{TPART *pn; /* ptr to part record in tree */
STRUCTASST(tpart.part, *partp);
pn = (TPART *)TR_FIND(&parts, &tpart, db_cmp_part);
if (pn == NULL) /* validation done in menu should prevent */
return (NO); /* non-existent part from reaching here */
STRUCTASST(pn->part, *partp);
return (YES);
}
/* (more) */
/* db_open_part - open a part record database */
void db_open_part()
{TR_OPEN(&parts);
}
/* db_close_part - close the part record database */
void db_close_part()
{TR_CLOSE(&parts);
}


