


There are many steps involved in writing a computer program to solve a given problem. The steps go from problem formulation and specification, to design of the solution, to implementation, testing and documentation, and finally to evaluation of the solution. This chapter outlines our approach to these steps. Subsequent chapters discuss the algorithms and data structures that are the building blocks of most computer programs.
Half the battle is knowing what problem to solve. When initially approached, most problems have no simple, precise specification. In fact, certain problems, such as creating a "gourmet" recipe or preserving world peace, may be impossible to formulate in terms that admit of a computer solution. Even if we suspect our problem can be solved on a computer, there is usually considerable latitude in several problem parameters. Often it is only by experimentation that reasonable values for these parameters can be found.
If certain aspects of a problem can be expressed in terms of a formal model, it is usually beneficial to do so, for once a problem is formalized, we can look for solutions in terms of a precise model and determine whether a program already exists to solve that problem. Even if there is no existing program, at least we can discover what is known about this model and use the properties of the model to help construct a good solution.
Almost any branch of mathematics or science can be called into service to help model some problem domain. Problems essentially numerical in nature can be modeled by such common mathematical concepts as simultaneous linear equations (e.g., finding currents in electrical circuits, or finding stresses in frames made of connected beams) or differential equations (e.g., predicting population growth or the rate at which chemicals will react). Symbol and text processing problems can be modeled by character strings and formal grammars. Problems of this nature include compilation (the translation of programs written in a programming language into machine language) and information retrieval tasks such as recognizing particular words in lists of titles owned by a library.
Once we have a suitable mathematical model for our problem, we can attempt to find a solution in terms of that model. Our initial goal is to find a solution in the form of an algorithm, which is a finite sequence of instructions, each of which has a clear meaning and can be performed with a finite amount of effort in a finite length of time. An integer assignment statement such as x := y + z is an example of an instruction that can be executed in a finite amount of effort. In an algorithm instructions can be executed any number of times, provided the instructions themselves indicate the repetition. However, we require that, no matter what the input values may be, an algorithm terminate after executing a finite number of instructions. Thus, a program is an algorithm as long as it never enters an infinite loop on any input.
There is one aspect of this definition of an algorithm that needs some clarification. We said each instruction of an algorithm must have a "clear meaning" and must be executable with a "finite amount of effort." Now what is clear to one person may not be clear to another, and it is often difficult to prove rigorously that an instruction can be carried out in a finite amount of time. It is often difficult as well to prove that on any input, a sequence of instructions terminates, even if we understand clearly what each instruction means. By argument and counterargument, however, agreement can usually be reached as to whether a sequence of instructions constitutes an algorithm. The burden of proof lies with the person claiming to have an algorithm. In Section 1.5 we discuss how to estimate the running time of common programming language constructs that can be shown to require a finite amount of time for their execution.
In addition to using Pascal programs as algorithms, we shall often present algorithms using a pseudo-language that is a combination of the constructs of a programming language together with informal English statements. We shall use Pascal as the programming language, but almost any common programming language could be used in place of Pascal for the algorithms we shall discuss. The following example illustrates many of the steps in our approach to writing a computer program.
Example 1.1. A mathematical model can be used to help design a traffic light for a complicated intersection of roads. To construct the pattern of lights, we shall create a program that takes as input a set of permitted turns at an intersection (continuing straight on a road is a "turn") and partitions this set into as few groups as possible such that all turns in a group are simultaneously permissible without collisions. We shall then associate a phase of the traffic light with each group in the partition. By finding a partition with the smallest number of groups, we can construct a traffic light with the smallest number of phases.
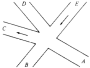
For example, the intersection shown in Fig. 1.1 occurs by a watering hole called JoJo's near Princeton University, and it has been known to cause some navigational difficulty, especially on the return trip. Roads C and E are oneway, the others two way. There are 13 turns one might make at this intersection. Some pairs of turns, like AB (from A to B) and EC, can be carried out simultaneously, while others, like AD and EB, cause lines of traffic to cross and therefore cannot be carried out simultaneously. The light at the intersection must permit turns in such an order that AD and EB are never permitted at the same time, while the light might permit AB and EC to be made simultaneously.
Fig. 1.1. An intersection.
We can model this problem with a mathematical structure known as a graph. A graph consists of a set of points called vertices, and lines connecting the points, called edges. For the traffic intersection problem we can draw a graph whose vertices represent turns and whose edges connect pairs of vertices whose turns cannot be performed simultaneously. For the intersection of Fig. 1.1, this graph is shown in Fig. 1.2, and in Fig. 1.3 we see another representation of this graph as a table with a 1 in row i and column j whenever there is an edge between vertices i and j.
The graph can aid us in solving the traffic light design problem. A coloring of a graph is an assignment of a color to each vertex of the graph so that no two vertices connected by an edge have the same color. It is not hard to see that our problem is one of coloring the graph of incompatible turns using as few colors as possible.
The problem of coloring graphs has been studied for many decades, and the theory of algorithms tells us a lot about this problem. Unfortunately, coloring an arbitrary graph with as few colors as possible is one of a large class of problems called "NP-complete problems," for which all known solutions are essentially of the type "try all possibilities." In the case of the coloring problem, "try all possibilities" means to try all assignments of colors to vertices using at first one color, then two colors, then three, and so on, until a legal coloring is found. With care, we can be a little speedier than this, but it is generally believed that no algorithm to solve this problem can be substantially more efficient than this most obvious approach.
We are now confronted with the possibility that finding an optimal solution for the problem at hand is computationally very expensive. We can adopt
Fig. 1.2. Graph showing incompatible turns.
Fig. 1.3. Table of incompatible turns.
one of three approaches. If the graph is small, we might attempt to find an optimal solution exhaustively, trying all possibilities. This approach, however, becomes prohibitively expensive for large graphs, no matter how efficient we try to make the program. A second approach would be to look for additional information about the problem at hand. It may turn out that the graph has some special properties, which make it unnecessary to try all possibilities in finding an optimal solution. The third approach is to change the problem a little and look for a good but not necessarily optimal solution. We might be happy with a solution that gets close to the minimum number of colors on small graphs, and works quickly, since most intersections are not even as complex as Fig. 1.1. An algorithm that quickly produces good but not necessarily optimal solutions is called a heuristic.
One reasonable heuristic for graph coloring is the following "greedy" algorithm. Initially we try to color as many vertices as possible with the first color, then as many as possible of the uncolored vertices with the second color, and so on. To color vertices with a new color, we perform the following steps.
This approach is called "greedy" because it colors a vertex whenever it can, without considering the potential drawbacks inherent in making such a move. There are situations where we could color more vertices with one color if we were less "greedy" and skipped some vertex we could legally color. For example, consider the graph of Fig. 1.4, where having colored vertex 1 red, we can color vertices 3 and 4 red also, provided we do not color 2 first. The greedy algorithm would tell us to color 1 and 2 red, assuming we considered vertices in numerical order.
Fig. 1.4. A graph.
As an example of the greedy approach applied to Fig. 1.2, suppose we start by coloring AB blue. We can color AC, AD, and BA blue, because none of these four vertices has an edge in common. We cannot color BC blue because there is an edge between AB and BC. Similarly, we cannot color BD, DA, or DB blue because each of these vertices is connected by an edge to one or more vertices already colored blue. However, we can color DC blue. Then EA, EB, and EC cannot be colored blue, but ED can.
Now we start a second color, say by coloring BC red. BD can be colored red, but DA cannot, because of the edge between BD and DA. Similarly, DB cannot be colored red, and DC is already blue, but EA can be colored red. Each other uncolored vertex has an edge to a red vertex, so no other vertex can be colored red.
The remaining uncolored vertices are DA, DB, EB, and EC. If we color DA green, then DB can be colored green, but EB and EC cannot. These two may be colored with a fourth color, say yellow. The colors are summarized in Fig. 1.5. The "extra" turns are determined by the greedy approach to be compatible with the turns already given that color, as well as with each other. When the traffic light allows turns of one color, it can also allow the extra turns safely.
Fig. 1.5. A coloring of the graph of Fig. 1.2.
The greedy approach does not always use the minimum possible number of colors. We can use the theory of algorithms again to evaluate the goodness of the solution produced. In graph theory, a k-clique is a set of k vertices, every pair of which is connected by an edge. Obviously, k colors are needed to color a k-clique, since no two vertices in a clique may be given the same color.
In the graph of Fig. 1.2 the set of four vertices AC, DA, BD, EB is a 4-clique. Therefore, no coloring with three or fewer colors exists, and the solution of Fig. 1.5 is optimal in the sense that it uses the fewest colors possible. In terms of our original problem, no traffic light for the intersection of Fig. 1.1 can have fewer than four phases.
Therefore, consider a traffic light controller based on Fig. 1.5, where each phase of the controller corresponds to a color. At each phase the turns indicated by the row of the table corresponding to that color are permitted, and the other turns are forbidden. This pattern uses as few phases as possible.
Once we have an appropriate mathematical model for a problem, we can formulate an algorithm in terms of that model. The initial versions of the algorithm are often couched in general statements that will have to be refined subsequently into smaller, more definite instructions. For example, we described the greedy graph coloring algorithm in terms such as "select some uncolored vertex." These instructions are, we hope, sufficiently clear that the reader grasps our intent. To convert such an informal algorithm to a program, however, we must go through several stages of formalization (called stepwise refinement) until we arrive at a program the meaning of whose steps are formally defined by a language manual.
Example 1.2. Let us take the greedy algorithm for graph coloring part of the way towards a Pascal program. In what follows, we assume there is a graph G, some of whose vertices may be colored. The following program greedy determines a set of vertices called newclr, all of which can be colored with a new color. The program is called repeatedly, until all vertices are colored. At a coarse level, we might specify greedy in pseudo-language as in Fig. 1.6.
procedure greedy ( var G: GRAPH; var newclr: SET );
{ greedy assigns to newclr a set of vertices of G that may be
given the same color }
begin
(1) newclr := Ø; †
(2) for each uncolored vertex v of G do
(3) if v is not adjacent to any vertex in newclr then begin
(4) mark v colored;
(5) add v to newclr
end
end; { greedy }
Fig. 1.6. First refinement of greedy algorithm.
We notice from Fig. 1.6 certain salient features of our pseudo-language. First, we use boldface lower case keywords corresponding to Pascal reserved words, with the same meaning as in standard Pascal. Upper case types such as GRAPH and SET‡ are the names of "abstract data types." They will be defined by Pascal type definitions and the operations associated with these abstract data types will be defined by Pascal procedures when we create the final program. We shall discuss abstract data types in more detail in the next two sections.
The flow-of-control constructs of Pascal, like if, for, and while, are available for pseudo-language statements, but conditionals, as in line (3), may be informal statements rather than Pascal conditional expressions. Note that the assignment at line (1) uses an informal expression on the right. Also, the for-loop at line (2) iterates over a set.
To be executed, the pseudo-language program of Fig. 1.6 must be refined into a conventional Pascal program. We shall not proceed all the way to such a program in this example, but let us give one example of refinement, transforming the if-statement in line (3) of Fig. 1.6 into more conventional code.
To test whether vertex v is adjacent to some vertex in newclr, we consider each member w of newclr and examine the graph G to see whether there is an edge between v and w. An organized way to make this test is to use found, a boolean variable to indicate whether an edge has been found. We can replace lines (3)-(5) of Fig. 1.6 by the code in Fig. 1.7.
procedure greedy ( var G: GRAPH; var newclr: SET );
begin
(1) newclr : = Ø;
(2) for each uncolored vertex v of G do begin
(3.1) found := false;
(3.2) for each vertex w in newclr do
(3.3) if there is an edge between v and w in G then
(3.4) found := true;
(3.5) if found = false then begin
{ v is adjacent to no vertex in newclr }
(4) mark v colored;
(5) add v to newclr
end
end
end; { greedy }
Fig. 1.7. Refinement of part of Fig. 1.6.
We have now reduced our algorithm to a collection of operations on two sets of vertices. The outer loop, lines (2)-(5), iterates over the set of uncolored vertices of G. The inner loop, lines (3.2)-(3.4), iterates over the vertices currently in the set newclr. Line (5) adds newly colored vertices to newclr.
There are a variety of ways to represent sets in a programming language like Pascal. In Chapters 4 and 5 we shall study several such representations. In this example we can simply represent each set of vertices by another abstract data type LIST, which here can be implemented by a list of integers terminated by a special value null (for which we might use the value 0). These integers might, for example, be stored in an array, but there are many other ways to represent LIST's, as we shall see in Chapter 2.
We can now replace the for-statement of line (3.2) in Fig. 1.7 by a loop, where w is initialized to be the first member of newclr and changed to be the next member, each time around the loop. We can also perform the same refinement for the for-loop of line (2) in Fig. 1.6. The revised procedure greedy is shown in Fig. 1.8. There is still more refinement to be done after Fig. 1.8, but we shall stop here to take stock of what we have done.
procedure greedy ( var G: GRAPH; var newclr: LIST );
{ greedy assigns to newclr those vertices that may be
given the same color }
var
found: boolean;
v, w: integer;
begin
newclr := Ø;
v := first uncolored vertex in G;
while v < > null do begin
found := false;
w := first vertex in newclr;
while w < > null do begin
if there is an edge between v and w in G then
found := true;
w := next vertex in newclr
end;
if found = false do begin
mark v colored;
add v to newclr
end;
v := next uncolored vertex in G
end
end; { greedy }
Fig. 1.8. Refined greedy procedure.
In Fig. 1.9 we see the programming process as it will be treated in this book. The first stage is modeling using an appropriate mathematical model such as a graph. At this stage, the solution to the problem is an algorithm expressed very informally.
At the next stage, the algorithm is written in pseudo-language, that is, a mixture of Pascal constructs and less formal English statements. To reach that stage, the informal English is replaced by progressively more detailed sequences of statements, in the process known as stepwise refinement. At some point the pseudo-language program is sufficiently detailed that the
Fig. 1.9. The problem solving process.
operations to be performed on the various types of data become fixed. We then create abstract data types for each type of data (except for the elementary types such as integers, reals and character strings) by giving a procedure name for each operation and replacing uses of each operation by an invocation of the corresponding procedure.
In the third stage we choose an implementation for each abstract data type and write the procedures for the various operations on that type. We also replace any remaining informal statements in the pseudo-language algorithm by Pascal code. The result is a running program. After debugging it will be a working program, and we hope that by using the stepwise development approach outlined in Fig. 1.9, little debugging will be necessary.
Most of the concepts introduced in the previous section should be familiar ideas from a beginning course in programming. The one possibly new notion is that of an abstract data type, and before proceeding it would be useful to discuss the role of abstract data types in the overall program design process. To begin, it is useful to compare an abstract data type with the more familiar notion of a procedure.
Procedures, an essential tool in programming, generalize the notion of an operator. Instead of being limited to the built-in operators of a programming language (addition, subtraction, etc.), by using procedures a programmer is free to define his own operators and apply them to operands that need not be basic types. An example of a procedure used in this way is a matrix multiplication routine.
Another advantage of procedures is that they can be used to encapsulate parts of an algorithm by localizing in one section of a program all the statements relevant to a certain aspect of a program. An example of encapsulation is the use of one procedure to read all input and to check for its validity. The advantage of encapsulation is that we know where to go to make changes to the encapsulated aspect of the problem. For example, if we decide to check that inputs are nonnegative, we need to change only a few lines of code, and we know just where those lines are.
We can think of an abstract data type (ADT) as a mathematical model with a collection of operations defined on that model. Sets of integers, together with the operations of union, intersection, and set difference, form a simple example of an ADT. In an ADT, the operations can take as operands not only instances of the ADT being defined but other types of operands, e.g., integers or instances of another ADT, and the result of an operation can be other than an instance of that ADT. However, we assume that at least one operand, or the result, of any operation is of the ADT in question.
The two properties of procedures mentioned above -- generalization and encapsulation -- apply equally well to abstract data types. ADT's are generalizations of primitive data types (integer, real, and so on), just as procedures are generalizations of primitive operations (+, -, and so on). The ADT encapsulates a data type in the sense that the definition of the type and all operations on that type can be localized to one section of the program. If we wish to change the implementation of an ADT, we know where to look, and by revising one small section we can be sure that there is no subtlety elsewhere in the program that will cause errors concerning this data type. Moreover, outside the section in which the ADT's operations are defined, we can treat the ADT as a primitive type; we have no concern with the underlying implementation. One pitfall is that certain operations may involve more than one ADT, and references to these operations must appear in the sections for both ADT's.
To illustrate the basic ideas, consider the procedure greedy of the previous section which, in Fig. 1.8, was implemented using primitive operations on an abstract data type LIST (of integers). The operations performed on the LIST newclr were:
There are many data structures that can be used to implement such lists efficiently, and we shall consider the subject in depth in Chapter 2. In Fig. 1.8, if we replace these operations by the statements
then we see an important aspect of abstract data types. We can implement a type any way we like, and the programs, such as Fig. 1.8, that use objects of that type do not change; only the procedures implementing the operations on the type need to change.
Turning to the abstract data type GRAPH we see need for the following operations:
There are clearly other operations needed outside the procedure greedy, such as inserting vertices and edges into the graph and making all vertices uncolored. There are many data structures that can be used to support graphs with these operations, and we shall study the subject of graphs in Chapters 6 and 7.
It should be emphasized that there is no limit to the number of operations that can be applied to instances of a given mathematical model. Each set of operations defines a distinct ADT. Some examples of operations that might be defined on an abstract data type SET are:
An implementation of an ADT is a translation, into statements of a programming language, of the declaration that defines a variable to be of that abstract data type, plus a procedure in that language for each operation of the ADT. An implementation chooses a data structure to represent the ADT; each data structure is built up from the basic data types of the underlying programming language using the available data structuring facilities. Arrays and record structures are two important data structuring facilities that are available in Pascal. For example, one possible implementation for variable S of type SET would be an array that contained the members of S.
One important reason for defining two ADT's to be different if they have the same underlying model but different operations is that the appropriateness of an implementation depends very much on the operations to be performed. Much of this book is devoted to examining some basic mathematical models such as sets and graphs, and developing the preferred implementations for various collections of operations.
Ideally, we would like to write our programs in languages whose primitive data types and operations are much closer to the models and operations of our ADT's. In many ways Pascal is not well suited to the implementation of various common ADT's but none of the programming languages in which ADT's can be declared more directly is as well known. See the bibliographic notes for information about some of these languages.
Although the terms "data type" (or just "type"), "data structure" and "abstract data type" sound alike, they have different meanings. In a programming language, the data type of a variable is the set of values that the variable may assume. For example, a variable of type boolean can assume either the value true or the value false, but no other value. The basic data types vary from language to language; in Pascal they are integer, real, boolean, and character. The rules for constructing composite data types out of basic ones also vary from language to language; we shall mention how Pascal builds such types momentarily.
An abstract data type is a mathematical model, together with various operations defined on the model. As we have indicated, we shall design algorithms in terms of ADT's, but to implement an algorithm in a given programming language we must find some way of representing the ADT's in terms of the data types and operators supported by the programming language itself. To represent the mathematical model underlying an ADT we use data structures, which are collections of variables, possibly of several different data types, connected in various ways.
The cell is the basic building block of data structures. We can picture a cell as a box that is capable of holding a value drawn from some basic or composite data type. Data structures are created by giving names to aggregates of cells and (optionally) interpreting the values of some cells as representing connections (e.g., pointers) among cells.
The simplest aggregating mechanism in Pascal and most other programming languages is the (one-dimensional) array, which is a sequence of cells of a given type, which we shall often refer to as the celltype. We can think of an array as a mapping from an index set (such as the integers 1, 2, . . . , n) into the celltype. A cell within an array can be referenced by giving the array name together with a value from the index set of the array. In Pascal the index set may be an enumerated type, such as (north, east, south, west), or a subrange type, such as 1..10. The values in the cells of an array can be of any one type. Thus, the declaration
name: array[indextype] of celltype;
declares name to be a sequence of cells, one for each value of type indextype; the contents of the cells can be any member of type celltype.
Incidentally, Pascal is somewhat unusual in its richness of index types. Many languages allow only subrange types (finite sets of consecutive integers) as index types. For example, to index an array by letters in Fortran, one must simulate the effect by using integer indices, such as by using index 1 to stand for 'A', 2 to stand for 'B', and so on.
Another common mechanism for grouping cells in programming languages is the record structure. A record is a cell that is made up of a collection of cells, called fields, of possibly dissimilar types. Records are often grouped into arrays; the type defined by the aggregation of the fields of a record becomes the "celltype" of the array. For example, the Pascal declaration
var
reclist: array[l..4] of record
data: real;
next: integer
end
declares reclist to be a four-element array, whose cells are records with two fields, data and next.
A third grouping method found in Pascal and some other languages is the file. The file, like the one-dimensional array, is a sequence of values of some particular type. However, a file has no index type; elements can be accessed only in the order of their appearance in the file. In contrast, both the array and the record are "random-access" structures, meaning that the time needed to access a component of an array or record is independent of the value of the array index or field selector. The compensating benefit of grouping by file, rather than by array, is that the number of elements in a file can be time-varying and unlimited.
In addition to the cell-grouping features of a programming language, we can represent relationships between cells using pointers and cursors. A pointer is a cell whose value indicates another cell. When we draw pictures of data structures, we indicate the fact that cell A is a pointer to cell B by drawing an arrow from A to B.
In Pascal, we can create a pointer variable ptr that will point to cells of a given type, say celltype, by the declaration
var
ptr: ?/FONT> celltype
A postfix up-arrow is used in Pascal as the dereferencing operator, so the expression ptr?/FONT> denotes the value (of type celltype) in the cell pointed to by ptr.
A cursor is an integer-valued cell, used as a pointer to an array. As a method of connection, the cursor is essentially the same as a pointer, but a cursor can be used in languages like Fortran that do not have explicit pointer types as Pascal does. By treating a cell of type integer as an index value for some array, we effectively make that cell point to one cell of the array. This technique, unfortunately, works only when cells of arrays are pointed to; there is no reasonable way to interpret an integer as a "pointer" to a cell that is not part of an array.
We shall draw an arrow from a cursor cell to the cell it "points to." Sometimes, we shall also show the integer in the cursor cell, to remind us that it is not a true pointer. The reader should observe that the Pascal pointer mechanism is such that cells in arrays can only be "pointed to" by cursors, never by true pointers. Other languages, like PL/I or C, allow components of arrays to be pointed to by either cursors or true pointers, while in Fortran or Algol, there being no pointer type, only cursors can be used.
Example 1.3. In Fig. 1.10 we see a two-part data structure that consists of a chain of cells containing cursors to the array reclist defined above. The purpose of the field next in reclist is to point to another record in the array. For example, reclist[4].next is 1, so record 4 is followed by record 1. Assuming record 4 is first, the next field of reclist orders the records 4, 1, 3, 2. Note that the next field is 0 in record 2, indicating that there is no following record. It is a useful convention, one we shall adopt in this book, to use 0 as a "NIL pointer," when cursors are being used. This idea is sound only if we also make the convention that arrays to which cursors "point" must be indexed starting at 1, never at 0.
Fig. 1.10. Example of a data structure.
The cells in the chain of records in Fig. 1.10 are of the type
type
recordtype = record
cursor: integer;
ptr: ?/FONT> recordtype
end
The chain is pointed to by a variable named header, which is of type ?/FONT> record-type; header points to an anonymous record of type recordtype.† That record has a value 4 in its cursor field; we regard this 4 as an index into the array reclist. The record has a true pointer in field ptr to another anonymous record. The record pointed to has an index in its cursor field indicating position 2 of reclist; it also has a nil pointer in its ptr field.
When solving a problem we are faced frequently with a choice among algorithms. On what basis should we choose? There are two often contradictory goals.
When we are writing a program to be used once or a few times, goal (1) is most important. The cost of the programmer's time will most likely exceed by far the cost of running the program, so the cost to optimize is the cost of writing the program. When presented with a problem whose solution is to be used many times, the cost of running the program may far exceed the cost of writing it, especially, if many of the program runs are given large amounts of input. Then it is financially sound to implement a fairly complicated algorithm, provided that the resulting program will run significantly faster than a more obvious program. Even in these situations it may be wise first to implement a simple algorithm, to determine the actual benefit to be had by writing a more complicated program. In building a complex system it is often desirable to implement a simple prototype on which measurements and simulations can be performed, before committing oneself to the final design. It follows that programmers must not only be aware of ways of making programs run fast, but must know when to apply these techniques and when not to bother.
The running time of a program depends on factors such as:
The fact that running time depends on the input tells us that the running time of a program should be defined as a function of the input. Often, the running time depends not on the exact input but only on the "size" of the input. A good example is the process known as sorting, which we shall discuss in Chapter 8. In a sorting problem, we are given as input a list of items to be sorted, and we are to produce as output the same items, but smallest (or largest) first. For example, given 2, 1, 3, 1, 5, 8 as input we might wish to produce 1, 1, 2, 3, 5, 8 as output. The latter list is said to be sorted smallest first. The natural size measure for inputs to a sorting program is the number of items to be sorted, or in other words, the length of the input list. In general, the length of the input is an appropriate size measure, and we shall assume that measure of size unless we specifically state otherwise.
It is customary, then, to talk of T(n), the running time of a program on inputs of size n. For example, some program may have a running time T(n) = cn2, where c is a constant. The units of T(n) will be left unspecified, but we can think of T(n) as being the number of instructions executed on an idealized computer.
For many programs, the running time is really a function of the particular input, and not just of the input size. In that case we define T(n) to be the worst case running time, that is, the maximum, over all inputs of size n, of the running time on that input. We also consider Tavg(n), the average, over all inputs of size n, of the running time on that input. While Tavg(n) appears a fairer measure, it is often fallacious to assume that all inputs are equally likely. In practice, the average running time is often much harder to determine than the worst-case running time, both because the analysis becomes mathematically intractable and because the notion of "average" input frequently has no obvious meaning. Thus, we shall use worst-case running time as the principal measure of time complexity, although we shall mention average-case complexity wherever we can do so meaningfully.
Now let us consider remarks (2) and (3) above: that the running time of a program depends on the compiler used to compile the program and the machine used to execute it. These facts imply that we cannot express the running time T(n) in standard time units such as seconds. Rather, we can only make remarks like "the running time of such-and-such an algorithm is proportional to n2." The constant of proportionality will remain unspecified since it depends so heavily on the compiler, the machine, and other factors.
To talk about growth rates of functions we use what is known as "big-oh" notation. For example, when we say the running time T(n) of some program is O(n2), read "big oh of n squared" or just "oh of n squared," we mean that there are positive constants c and n0 such that for n equal to or greater than n0, we have T(n) ?/FONT> cn2.
Example 1.4. Suppose T(0) = 1, T(1) = 4, and in general T(n) = (n+l)2. Then we see that T(n) is O(n2), as we may let n0 = 1 and c = 4. That is, for n ?/FONT> 1, we have (n + 1)2 ?/FONT> 4n2, as the reader may prove easily. Note that we cannot let n0 = 0, because T(0) = 1 is not less than c02 = 0 for any constant c.
In what follows, we assume all running-time functions are defined on the nonnegative integers, and their values are always nonnegative, although not necessarily integers. We say that T(n) is O(f(n)) if there are constants c and n0 such that T(n) ?/FONT> cf(n) whenever n ?/FONT> n0. A program whose running time is O(f (n)) is said to have growth rate f(n).
Example 1.5. The function T(n)= 3n3 + 2n2 is O(n3). To see this, let n0 = 0 and c = 5. Then, the reader may show that for n ?/FONT> 0, 3n3 + 2n2 ?/FONT> 5n3. We could also say that this T(n) is O(n4), but this would be a weaker statement than saying it is O(n3).
As another example, let us prove that the function 3n is not O (2n). Suppose that there were constants n0 and c such that for all n ?/FONT> n0, we had 3n ?/FONT> c2n. Then c ?/FONT> (3/2)n for any n ?/FONT> n0. But (3/2)n gets arbitrarily large as n gets large, so no constant c can exceed (3/2)n for all n.
When we say T(n) is O(f(n)), we know that f(n) is an upper bound on the growth rate of T(n). To specify a lower bound on the growth rate of T(n) we can use the notation T(n) is W(g(n)), read "big omega of g(n)" or just "omega of g(n)," to mean that there exists a positive constant c such that T(n) ?/FONT> cg(n) infinitely often (for an infinite number of values of n).†
Example 1.6. To verify that the function T(n)= n3 + 2n2 is W(n3), let c = 1. Then T(n) ?/FONT> cn3 for n = 0, 1, . . ..
For another example, let T(n) = n for odd n ?/FONT> 1 and T(n) = n2/100 for even n ?/FONT> 0. To verify that T(n) is W (n2), let c = 1/100 and consider the infinite set of n's: n = 0, 2, 4, 6, . . ..
We shall assume that programs can be evaluated by comparing their running-time functions, with constants of proportionality neglected. Under this assumption a program with running time O(n2) is better than one with running time O(n3), for example. Besides constant factors due to the compiler and machine, however, there is a constant factor due to the nature of the program itself. It is possible, for example, that with a particular compiler-machine combination, the first program takes 100n2 milliseconds, while the second takes 5n3 milliseconds. Might not the 5n3 program be better than the 100n2 program?
The answer to this question depends on the sizes of inputs the programs are expected to process. For inputs of size n < 20, the program with running time 5n3 will be faster than the one with running time 100n2. Therefore, if the program is to be run mainly on inputs of small size, we would indeed prefer the program whose running time was O(n3). However, as n gets large, the ratio of the running times, which is 5n3/100n2 = n/20, gets arbitrarily large. Thus, as the size of the input increases, the O(n3) program will take significantly more time than the O(n2) program. If there are even a few large inputs in the mix of problems these two programs are designed to solve, we can be much better off with the program whose running time has the lower growth rate.
Another reason for at least considering programs whose growth rates are as low as possible is that the growth rate ultimately determines how big a problem we can solve on a computer. Put another way, as computers get faster, our desire to solve larger problems on them continues to increase. However, unless a program has a low growth rate such as O(n) or O(nlogn), a modest increase in computer speed makes very little difference in the size of the largest problem we can solve in a fixed amount of time.
Example 1.7. In Fig. 1.11 we see the running times of four programs with different time complexities, measured in seconds, for a particular compiler-machine combination. Suppose we can afford 1000 seconds, or about 17 minutes, to solve a given problem. How large a problem can we solve? In 103 seconds, each of the four algorithms can solve roughly the same size problem, as shown in the second column of Fig. 1.12.
Fig. 1.11. Running times of four programs.
Suppose that we now buy a machine that runs ten times faster at no additional cost. Then for the same cost we can spend 104 seconds on a problem where we spent 103 seconds before. The maximum size problem we can now solve using each of the four programs is shown in the third column of Fig. 1.12, and the ratio of the third and second columns is shown in the fourth column. We observe that a 1000% improvement in computer speed yields only a 30% increase in the size of problem we can solve if we use the O(2n) program. Additional factors of ten speedup in the computer yield an even smaller percentage increase in problem size. In effect, the O(2n) program can solve only small problems no matter how fast the underlying computer.
Fig. 1.12. Effect of a ten-fold speedup in computation time.
In the third column of Fig. 1.12 we see the clear superiority of the O(n) program; it returns a 1000% increase in problem size for a 1000% increase in computer speed. We see that the O(n3) and O(n2) programs return, respectively, 230% and 320% increases in problem size for 1000% increases in speed. These ratios will be maintained for additional increases in speed.
As long as the need for solving progressively larger problems exists, we are led to an almost paradoxical conclusion. As computation becomes cheaper and machines become faster, as will most surely continue to happen, our desire to solve larger and more complex problems will continue to increase. Thus, the discovery and use of efficient algorithms, those whose growth rates are low, becomes more rather than less important.
We wish to re-emphasize that the growth rate of the worst case running time is not the sole, or necessarily even the most important, criterion for evaluating an algorithm or program. Let us review some conditions under which the running time of a program can be overlooked in favor of other issues.
Determining, even to within a constant factor, the running time of an arbitrary program can be a complex mathematical problem. In practice, however, determining the running time of a program to within a constant factor is usually not that difficult; a few basic principles suffice. Before presenting these principles, it is important that we learn how to add and multiply in "big oh" notation.
Suppose that T1(n) and T2(n) are the running times of two program fragments P1 and P2, and that T1(n) is O(f(n)) and T2(n) is O(g(n)). Then T1(n)+T2(n), the running time of P1 followed by P2, is O(max(f(n),g(n))). To see why, observe that for some constants c1, c2, n1, and n2, if n ?/FONT> n1 then T1(n) ?/FONT> c1f(n), and if n ?/FONT> n2 then T2(n) ?/FONT> c2g(n). Let n0 = max(n1, n2). If n ?/FONT> n0, then T1(n) + T2(n) ?/FONT> c1f(n) + c2g(n). From this we conclude that if n ?/FONT> n0, then T1(n) + T2(n) ?/FONT> (c1 + c2)max(f(n), g(n)). Therefore, the combined running time T1(n) + T2(n) is O (max(f (n), g (n))).
Example 1.8. The rule for sums given above can be used to calculate the running time of a sequence of program steps, where each step may be an arbitrary program fragment with loops and branches. Suppose that we have three steps whose running times are, respectively, O(n2), O(n3) and O(n log n). Then the running time of the first two steps executed sequentially is O(max(n2, n3)) which is O(n3). The running time of all three together is O(max(n3, n log n)) which is O(n3).
In general, the running time of a fixed sequence of steps is, to within a constant factor, the running time of the step with the largest running time. In rare circumstances there will be two or more steps whose running times are incommensurate (neither is larger than the other, nor are they equal). For example, we could have steps of running times O(f (n)) and O(g (n)), where
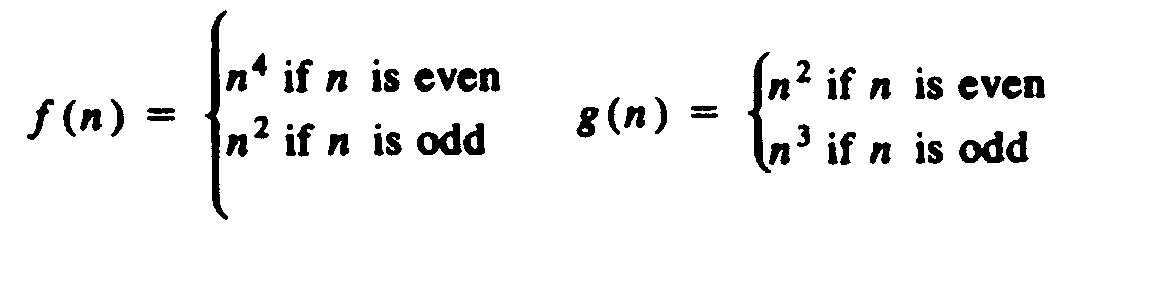
In such cases the sum rule must be applied directly; the running time is O(max(f(n), g(n))), that is, n4 if n is even and n3 if n is odd.
Another useful observation about the sum rule is that if g(n) ?/FONT> f(n) for all n above some constant n0, then O(f(n) + g(n)) is the same as O(f(n)). For example, O(n2+n) is the same as O(n2).
The rule for products is the following. If T1(n) and T2(n) are O(f(n)) and O(g(n)), respectively, then T1(n)T2(n) is O(f(n)g(n)). The reader should prove this fact using the same ideas as in the proof of the sum rule. It follows from the product rule that O(cf(n)) means the same thing as O(f(n)) if c is any positive constant. For example, O(n2/2) is the same as O(n2).
Before proceeding to the general rules for analyzing the running times of programs, let us take a simple example to get an overview of the process.
Example 1.9. Consider the sorting program bubble of Fig. 1.13, which sorts an array of integers into increasing order. The net effect of each pass of the inner loop of statements (3)-(6) is to "bubble" the smallest element toward the front of the array.
procedure bubble ( var A: array [1..n] of integer );
{ bubble sorts array A into increasing order }
var
i, j, temp: integer;
begin
(1) for i := 1 to n-1 do
(2) for j := n downto i+1 do
(3) if A[j-1] > A[j] then begin
{ swap A[j - 1] and A[j] }
(4) temp := A[j-1];
(5) A[j-1] := A[j];
(6) AI> [j] := temp
end
end; { bubble }
Fig. 1.13. Bubble sort.
The number n of elements to be sorted is the appropriate measure of input size. The first observation we make is that each assignment statement takes some constant amount of time, independent of the input size. That is to say, statements (4), (5) and (6) each take O(1) time. Note that O(1) is "big oh" notation for "some constant amount." By the sum rule, the combined running time of this group of statements is O(max(1, 1, 1)) = O(1).
Now we must take into account the conditional and looping statements. The if- and for-statements are nested within one another, so we may work from the inside out to get the running time of the conditional group and each loop. For the if-statement, testing the condition requires O(1) time. We don't know whether the body of the if-statement (lines (4)-(6)) will be executed. Since we are looking for the worst-case running time, we assume the worst and suppose that it will. Thus, the if-group of statements (3)-(6) takes O(1) time.
Proceeding outward, we come to the for-loop of lines (2)-(6). The general rule for a loop is that the running time is the sum, over each iteration of the loop, of the time spent executing the loop body for that iteration. We must, however, charge at least O(1) for each iteration to account for incrementing the index, for testing to see whether the limit has been reached, and for jumping back to the beginning of the loop. For lines (2)-(6) the loop body takes O(1) time for each iteration. The number of iterations of the loop is n-i, so by the product rule, the time spent in the loop of lines (2)-(6) is O((n-i) X 1) which is O(n-i).
Now let us progress to the outer loop, which contains all the executable statements of the program. Statement (1) is executed n - 1 times, so the total running time of the program is bounded above by some constant times
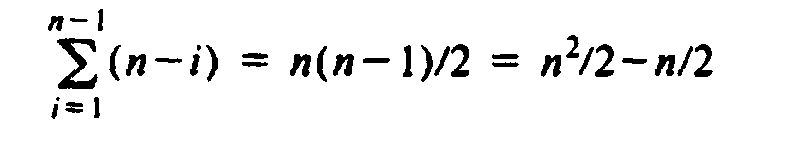
which is O(n2). The program of Fig. 1.13, therefore, takes time proportional to the square of the number of items to be sorted. In Chapter 8, we shall give sorting programs whose running time is O(nlogn), which is considerably smaller, since for large n, logn† is very much smaller than n.
Before proceeding to some general analysis rules, let us remember that determining a precise upper bound on the running time of programs is sometimes simple, but at other times it can be a deep intellectual challenge. There are no complete sets of rules for analyzing programs. We can only give the reader some hints and illustrate some of the subtler points by examples throughout this book.
Now let us enumerate some general rules for the analysis of programs. In general, the running time of a statement or group of statements may be parameterized by the input size and/or by one or more variables. The only permissible parameter for the running time of the whole program is n, the input size.
If we have a program with procedures, none of which is recursive, then we can compute the running time of the various procedures one at a time, starting with those procedures that make no calls on other procedures. (Remember to count a function invocation as a "call.") There must be at least one such procedure, else at least one procedure is recursive. We can then evaluate the running time of procedures that call only procedures that make no calls, using the already-evaluated running times of the called procedures. We continue this process, evaluating the running time of each procedure after the running times of all procedures it calls have been evaluated.
If there are recursive procedures, then we cannot find an ordering of all the procedures so that each calls only previously evaluated procedures. What we must now do is associate with each recursive procedure an unknown time function T(n), where n measures the size of the arguments to the procedure. We can then get a recurrence for T(n), that is, an equation for T(n) in terms of T(k) for various values of k.
Techniques for solving many different kinds of recurrences exist; we shall present some of these in Chapter 9. Here we shall show how to analyze a simple recursive program.
Example 1.10. Figure 1.14 gives a recursive program to compute n!, the product of all the integers from 1 to n inclusive.
An appropriate size measure for this function is the value of n. Let T(n) be the running time for fact(n). The running time for lines (1) and (2) is O(1), and for line (3) it is O(1) + T(n-1). Thus, for some constants c and d,
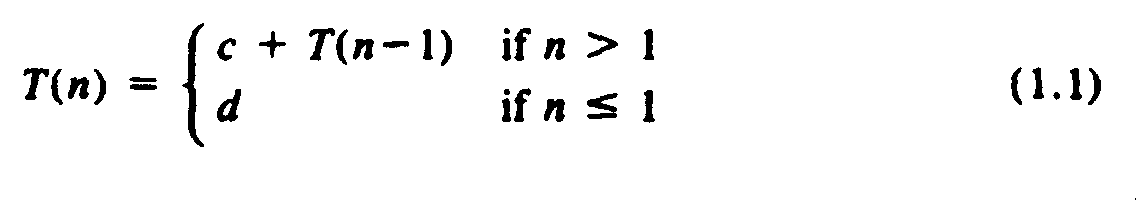
function fact ( n: integer ): integer;
{ fact(n) computes n! }
begin
(1) if n <= 1 then
(2) fact := 1
else
(3) fact := n * fact(n-1)
end; { fact }
Fig. 1.14. Receursive program to compute factorials.
Assuming n > 2, we can expand T(n-1) in (1.1) to obtain
T(n) = 2c + T(n-2) if n > 2
That is, T(n-1) = c + T(n-2), as can be seen by substituting n-1 for n in (1.1). Thus, we may substitute c + T(n-2) for T(n-1) in the equation T(n) = c + T(n-1). We can then use (1.1) to expand T(n-2) to obtain
T(n) = 3c + T(n-3) if n > 3
and so on. In general,
T(n) = ic + T(n-i) if n > i
Finally, when i = n-1 we get
T(n) = c(n-1) + T(1) = c(n-1) + d (1.2)
From (1.2) we can conclude that T(n) is O(n). We should note that in this analysis we have assumed that the multiplication of two integers is an O(1) operation. In practice, however, we cannot use the program in Fig. 1.14 to compute n! for large values of n, because the size of the integers being computed will exceed the word length of the underlying machine.
The general method for solving recurrence equations, as typified by Example 1.10, is repeatedly to replace terms T(k) on the right side of the equation by the entire right side with k substituted for n, until we obtain a formula in which T does not appear on the right as in (1.2). Often we must then sum a series or, if we cannot sum it exactly, get a close upper bound on the sum to obtain an upper bound on T(n).
In analyzing the running time of a program we have tacitly assumed that all flow of control within a procedure was determined by branching and 1ooping constructs. We relied on this fact as we determined the running time of progressively larger groups of statements by assuming that we needed only the sum rule to group sequences of statements together. Goto statments, however, make the logical grouping of statements more complex. For this reason, goto statements should be avoided, but Pascal lacks break- and continue-statements to jump out of loops. The goto-statement is often used as a substitute for statements of this nature in Pascal.
We suggest the following approach to handling goto's that jump from a loop to code that is guaranteed to follow the loop, which is generally the only kind of goto that is justified. As the goto is presumably executed conditionally within the loop, we may pretend that it is never taken. Because the goto takes us to a statement that will be executed after the loop completes, this assumption is conservative; we can never underestimate the worst case running time of the program if we assume the loop runs to completion. However, it is a rare program in which ignoring the goto is so conservative that it causes us to overestimate the growth rate of the worst case running time for the program. Notice that if we were faced with a goto that jumped back to previously executed code we could not ignore it safely, since that goto may create a loop that accounts for the bulk of the running time.
We should not leave the impression that the use of backwards goto's by themselves make running times unanalyzable. As long as the loops of a program have a reasonable structure, that is, each pair of loops are either disjoint or nested one within the other, then the approach to running time analysis described in this section will work. (However, it becomes the responsibility of the analyzer to ascertain what the loop structure is.) Thus, we should not hesitate to apply these methods of program analysis to a language like Fortran, where goto's are essential, but where programs written in the language tend to have a reasonable loop structure.
If we know the growth rate of the time needed to execute informal English statements, we can analyze pseudo-programs just as we do real ones. Often, however, we do not know the time to be spent on not-fully-implemented parts of a pseudo-program. For example, if we have a pseudo-program in which the only unimplemented parts are operations on ADT's, one of several implementations for an ADT may be chosen, and the overall running time may depend heavily on the implementation. Indeed, one of the reasons for writing programs in terms of ADT's is so we can consider the trade-offs among the running times of the various operations that we obtain by different implementations.
To analyze pseudo-programs consisting of programming language statements and calls to unimplemented procedures, such as operations on ADT's, we compute the running time as a function of unspecified running times for each procedure. The running time for a procedure will be parameterized by the "size" of the argument or arguments for that procedure. Just as for "input size," the appropriate measure of size for an argument is a matter for the analyzer to decide. If the procedure is an operation on an ADT, then the underlying mathematical model for the ADT often indicates the logical notion of size. For example, if the ADT is based on sets, the number of elements in a set is often the right notion of size. In the remaining chapters we shall see many examples of analyzing the running time of pseudo-programs.
There are a substantial number of ideas we should bear in mind when designing an algorithm and implementing it as a program. These ideas often appear platitudinous, because by-and-large they can be appreciated only through their successful use in real problems, rather than by development of a theory. They are sufficiently important, however, that they are worth repeating here. The reader should watch for the application of these ideas in the programs designed in this book, as well as looking for opportunities to put them into practice in his own programs.
Example 1.11. As an example, let us consider the program spell, as it was originally written by S.C. Johnson from UNIX† commands. This program takes as input a file f1consisting of English text and produces as output all those words in f1that are not found in a small dictionary.‡ spell tends to list proper names as misspellings and may also list real words not in its dictionary, but the typical output of spell is short enough that it can be scanned by eye, and human intelligence can be used to determine whether a word in the output of spell is a misspelling. (This book was checked using spell.)
The first filter used by spell is a command called translate that, given appropriate parameters, replaces capital letters by lower case letters and blanks by newlines, leaving other characters unchanged. The output of translate consists of a file f2 that has the words of f1, uncapitalized, one to a line. Next comes a command sort that sorts the lines of its input file into lexicographic (alphabetical) order. The output of sort is a file f3 that has all the words of f2 in alphabetical order, with repetitions. Then a command unique removes duplicate lines from its input file, producing an output file f4 that has the words of the original file, without capitalization or duplicates, in alphabetical order. Finally, a command diff, with a parameter indicating a second file f5 that holds the alphabetized list of words in the dictionary, one to a line, is applied to f4. The result is all words in f4 (and hence f1) but not in f5, i.e., all words in the original input that are not in the dictionary. The complete program spell is just the following sequence of commands.
spell : translate [A-Z] ?/FONT> [a-z], blank ?/FONT> newline
sort
unique
diff dictionary
Command level programming requires discipline from a community of programmers; they must write programs as filters wherever possible, and they must write tools instead of special purpose programs wherever possible. Yet the reward, in terms of the overall ratio of work to results, is substantial.
Most of the programs written in this book are in Pascal. To make programs more readable, however, we occasionally use three constructs not found in standard Pascal, each of which can be mechanically translated into pure Pascal. One such construct is the nonnumeric label. The few times we need labels, we shall use nonnumeric labels since they make programs easier to understand. For example, "goto output" is invariably more meaningful than "goto 561." To convert a program containing nonnumeric labels into pure Pascal, we must replace each nonnumeric label by a distinct numeric label and we must then declare those labels with a label declaration at the beginning of the program. This process can be clone mechanically.
The second nonstandard construct is the return statement, which we use because it allows us to write more understandable programs without using goto statements to interrupt the flow of control. The return statement we use has the form
return (expression)
where the (expression) is optional. We can convert a procedure containing return statements into a standard Pascal program quite simply. First, we declare a new label, say 999, and let it label the last end statement of the procedure. If the statement return (x) appears in a function zap, say, we replace this statement with the block
begin zap := x; goto 999 end
In a procedure, the statement return, which can have no argument, is simply replaced by goto 999.
Example 1.12. Figure 1.15 shows the factorial program written using return statements. Figure 1.16 shows the resulting Pascal program if we apply this transformation systematically to Fig. 1.15.
function fact ( n: integer ): integer;
begin
if n <= l then
return (1)
else
return ( n * fact(n- 1))
end; { fact }
Fig. 1.15. Factorial program with return statements.
The third extension is that we use expressions as names of types
function fact ( n: integer ) :integer;
label
999;
begin
if n <= 1 then
begin
fact := 1;
goto 999
end
else
begin
fact := n * fact(n - 1);
goto 999
end
999:
end; { fact }
Fig. 1.16. Resulting Pascal program.
uniformly throughout a program. For example, an expression like ?/FONT> celltype, while permissible everywhere else, is not permitted as the type of a parameter of a procedure or the type of the value returned by a function. Technically, Pascal requires that we invent a name for the type expression, say ptrtocell. In this book, we shall allow such expressions, expecting that the reader could invent such a type name and mechanically replace type expressions by the type name. Thus, we shall write statements like
function zap ( A: array[1..10] of integer ) : ?/FONT> celltype
to stand for
function zap (A: arrayoftenints ) : ptrtocell
Finally, a note on our typesetting conventions for programs. Pascal reserved words are in boldface, types are in roman, and procedure, function, and variable names are in italic. We distinguish between upper and lower case letters.
| 1.1 | There are six teams in the football league: the Vultures, the Lions, the Eagles, the Beavers, the Tigers, and the Skunks. The Vultures have already played the Lions and the Eagles; the Lions have also played the Beavers and Skunks. The Tigers have played the Eagles and Skunks. Each team plays one game per week. Find a schedule so that all teams will have played each other in the fewest number of weeks. Hint. Create a graph whose vertices are the pairs of teams that have not yet played each other. What should the edges be so that in a legal coloring of the graph, each color can represent the games played in one week? | ||||||
|---|---|---|---|---|---|---|---|
| *1.2 | Consider a robot arm that is fixed at one end. The arm contains two elbows at each of which it is possible to rotate the arm 90 degrees up and down in a vertical plane. How would you mathematically model the possible movements of the end of the arm? Describe an algorithm to move the end of the robot arm from one permissible position to another. | ||||||
| *1.3 | Suppose we wish to multiply four matrices of real numbers M1 × M2 × M3 × M4 where M1 is 10 by 20, M2 is 20 by 50, M3 is 50 by 1, and M4 is 1 by 100. Assume that the multiplication of a p × q matrix by a q × r matrix requires pqr scalar operations, as it does in the usual matrix multiplication algorithm. Find the optimal order in which to multiply the matrices so as to minimize the total number of scalar operations. How would you find this optimal ordering if there are an arbitrary number of matrices? | ||||||
| **1.4 | Suppose we wish to partition the square roots of the integers from 1 to 100 into two piles of fifty numbers each, such that the sum of the numbers in the first pile is as close as possible to the sum of the numbers in the second pile. If we could use two minutes of computer time to help answer this question, what computations would you perform in those two minutes? | ||||||
| 1.5 | Describe a greedy algorithm for playing chess. Would you expect it to perform very well? | ||||||
| 1.6 | In Section 1.2 we considered an ADT SET, with operations MAKE-NULL, UNION, and SIZE. Suppose for convenience that we assume all sets are subsets of {0, 1, . . . , 31} and let the ADT SET be interpreted as the Pascal data type set of 0..31. Write Pascal procedures for these operations using this implementation of SET. | ||||||
| 1.7 | The greatest common divisor of two integers p and q is the largest
integer d that divides both p and q evenly. We wish to develop a
program for computing the greatest common divisor of two integers p
and q using the following algorithm. Let r be the remainder of p
divided by q. If r is O, then q is the greatest common divisor.
Otherwise, set p equal to q, then q equal to r, and repeat the process.
|
||||||
| 1.8 | We want to develop a program for a text formatter that will place
words on lines that are both left and right justified. The program will
have a word buffer and a line buffer. Initially both are empty. A
word is read into the word buffer. If there is sufficient room in the
line buffer, the word is transferred to the line buffer. Otherwise,
additional spaces are inserted between words in the line buffer to fill
out the line, and then the line buffer is emptied by printing the line.
|
||||||
| 1.9 | Consider a set of n cities and a table of distances between pairs of cities. Write a pseudo-language program for finding a short path that goes through each city exactly once and returns to the city from which it started. There is no known method for obtaining the shortest such tour except by exhaustive searching. Thus try to find an efficient algorithm for this problem using some reasonable heuristic. | ||||||
| 1.10 | Consider the following functions of n:
Indicate for each distinct pair i and j whether fi(n) is O(fj(n)) and whether fi(n) is W(fj(n)). |
||||||
| 1.11 | Consider the following functions of n:
Indicate for each distinct pair i and j whether gi(n) is O(gj(n)) and whether gi(n) is W(gj(n)). |
||||||
| 1.12 | Give, using "big oh" notation, the worst case running times of the
following procedures as a function of n.
|
||||||
| 1.13 | Show that the following statements are true.
|
||||||
| *1.14 | Suppose T1(n) is W(f(n)) and T2(n) is W(g(n)). Which of the
following statements are true?
| ||||||
| *1.15 | Some authors define big omega by saying f(n) is W(g(n)) if there is
some n0 and c > 0 such that for all n ?/FONT> n0 we have f(n) ?/FONT> cg(n).
1.16 |
Order the following functions by growth rate: (a) n, (b) ?/FONT>?I>n, (c)
logn, (d) loglogn, (e) log2n, (f) n/logn, (g) ?/FONT>?I>nlog2n, (h) (1/3)n, (i)
(3/2)n, (j) 17. |
1.17 |
Assume the parameter n in the procedure below is a positive power of
2, i.e., n = 2, 4, 8, 16 , . . .. Give the formula that expresses the
value of the variable count in terms of the value of n when the
procedure terminates.
|
procedure mystery ( n: integer );
1.18 |
Here is a function max(i, n) that returns the largest element in
positions i through i+n-1 of an integer array A. You may assume for
convenience that n is a power of 2.
|
|
The concept of an abstract data type can be traced to the class type in the language SIMULA 67 (Birtwistle et al. [1973]). Since that time, a variety of other languages that support abstract data types have been developed including Alphard (Shaw, Wulf, and London [1977]), C with classes (Stroustrup [1982]), CLU (Liskov, et al. [1977]), MESA (Geschke, Morris, and Satterthwaite [1977]), and Russell (Demers and Donahue [1979]). The ADT concept is further discussed in works such as Gotlieb and Gotlieb [1978] and Wulf et al. [1981].
Knuth [1968] was the first major work to advocate the systematic study of the running time of programs. Aho, Hopcroft, and Ullman [1974] relate the time and space complexity of algorithms to various models of computation, such as Turing machines and random-access machines. See also the bibliographic notes to Chapter 9 for more references to the subject of analysis of algorithms and programs.
For additional material on structured programming see Hoare, Dahl, and Dijkstra [1972], Wirth [1973], Kernighan and Plauger [1974], and Yourdon and Constantine [1975]. Organizational and psychological problems arising in the development of large software projects are discussed in Brooks [1974] and Weinberg [1971]. Kernighan and Plauger [1981] show how to build useful software tools for a programming environment.
† The symbol Ø stands for the empty set.
‡ We distinguish the abstract data type SET from the built-in set type of Pascal.
† The record has no known name because it was created by a call new(header), which made header point to this newly-created record. Internal to the machine, however, there is a memory address that can be used to locate the cell.
† Note the asymmetry between big-oh and big-omega notation. The reason such asymmetry is often useful is that there are many times when an algorithm is fast on many but not all inputs. For example, there are algorithms to test whether their input is of prime length that run very fast whenever that length is even, so we could not get a good lower bound on running time that held for all n ?/FONT> n0.
† Unless otherwise specified all logarithms are to the base 2. Note that O(logn) does not depend on the base of the logarithm since logan = clogbn, where c = logab.
† UNIX is a Trademark of Bell Laboratories.
‡ We could use an unabridged dictionary, but many misspellings are real words one has never heard of.