(i) machines for executing algorithms--this area includes everything from the smallest pocket calculator to the largest general purpose digital computer. The goal is to study various forms of machine fabrication and organization so that algorithms can be effectively carried out.
(ii) languages for describing algorithms--these languages can be placed on a continuum. At one end are the languages which are closest to the physical machine and at the other end are languages designed for sophisticated problem solving. One often distinguishes between two phases of this area: language design and translation. The first calls for methods for specifying the syntax and semantics of a language. The second requires a means for translation into a more basic set of commands.
(iii) foundations of algorithms--here people ask and try to answer such questions as: is a particular task accomplishable by a computing device; or what is the minimum number of operations necessary for any algorithm which performs a certain function? Abstract models of computers are devised so that these properties can be studied.
(iv) analysis of algorithms--whenever an algorithm can be specified it makes sense to wonder about its behavior. This was realized as far back as 1830 by Charles Babbage, the father of computers. An algorithm's behavior pattern or performance profile is measured in terms of the computing time and space that are consumed while the algorithm is processing. Questions such as the worst and average time and how often they occur are typical.
We see that in this definition of computer science, "algorithm" is a fundamental notion. Thus it deserves a precise definition. The dictionary's definition "any mechanical or recursive computational procedure" is not entirely satisfying since these terms are not basic enough.
Definition: An algorithm is a finite set of instructions which, if followed, accomplish a particular task. In addition every algorithm must satisfy the following criteria:
(i) input: there are zero or more quantities which are externally supplied;
(ii) output: at least one quantity is produced;
(iii) definiteness: each instruction must be clear and unambiguous;
(iv) finiteness: if we trace out the instructions of an algorithm, then for all cases the algorithm will terminate after a finite number of steps;
(v) effectiveness: every instruction must be sufficiently basic that it can in principle be carried out by a person using only pencil and paper. It is not enough that each operation be definite as in (iii), but it must also be feasible.
In formal computer science, one distinguishes between an algorithm, and a program. A program does not necessarily satisfy condition (iv). One important example of such a program for a computer is its operating system which never terminates (except for system crashes) but continues in a wait loop until more jobs are entered. In this book we will deal strictly with programs that always terminate. Hence, we will use these terms interchangeably.
An algorithm can be described in many ways. A natural language such as English can be used but we must be very careful that the resulting instructions are definite (condition iii). An improvement over English is to couple its use with a graphical form of notation such as flowcharts. This form places each processing step in a "box" and uses arrows to indicate the next step. Different shaped boxes stand for different kinds of operations. All this can be seen in figure 1.1 where a flowchart is given for obtaining a Coca-Cola from a vending machine. The point is that algorithms can be devised for many common activities.
Have you studied the flowchart? Then you probably have realized that it isn't an algorithm at all! Which properties does it lack?
Returning to our earlier definition of computer science, we find it extremely unsatisfying as it gives us no insight as to why the computer is revolutionizing our society nor why it has made us re-examine certain basic assumptions about our own role in the universe. While this may be an unrealistic demand on a definition even from a technical point of view it is unsatisfying. The definition places great emphasis on the concept of algorithm, but never mentions the word "data". If a computer is merely a means to an end, then the means may be an algorithm but the end is the transformation of data. That is why we often hear a computer referred to as a data processing machine. Raw data is input and algorithms are used to transform it into refined data. So, instead of saying that computer science is the study of algorithms, alternatively, we might say that computer science is the study of data:
(i) machines that hold data;
(ii) languages for describing data manipulation;
(iii) foundations which describe what kinds of refined data can be produced from raw data;
(iv) structures for representing data.
There is an intimate connection between the structuring of data, and the synthesis of algorithms. In fact, a data structure and an algorithm should be thought of as a unit, neither one making sense without the other. For instance, suppose we have a list of n pairs of names and phone numbers (a1,b1)(a2,b2), ..., (an,bn), and we want to write a program which when given any name, prints that person's phone number. This task is called searching. Just how we would write such an algorithm critically depends upon how the names and phone numbers are stored or structured. One algorithm might just forge ahead and examine names, a1,a2,a3, ... etc., until the correct name was found. This might be fine in Oshkosh, but in Los Angeles, with hundreds of thousands of names, it would not be practical. If, however, we knew that the data was structured so that the names were in alphabetical order, then we could do much better. We could make up a second list which told us for each letter in the alphabet, where the first name with that letter appeared. For a name beginning with, say, S, we would avoid having to look at names beginning with other letters. So because of this new structure, a very different algorithm is possible. Other ideas for algorithms become possible when we realize that we can organize the data as we wish. We will discuss many more searching strategies in Chapters 7 and 9.
Therefore, computer science can be defined as the study of data, its representation and transformation by a digital computer. The goal of this book is to explore many different kinds of data objects. For each object, we consider the class of operations to be performed and then the way to represent this object so that these operations may be efficiently carried out. This implies a mastery of two techniques: the ability to devise alternative forms of data representation, and the ability to analyze the algorithm which operates on that structure . The pedagogical style we have chosen is to consider problems which have arisen often in computer applications. For each problem we will specify the data object or objects and what is to be accomplished. After we have decided upon a representation of the objects, we will give a complete algorithm and analyze its computing time. After reading through several of these examples you should be confident enough to try one on your own.
There are several terms we need to define carefully before we proceed. These include data structure, data object, data type and data representation. These four terms have no standard meaning in computer science circles, and they are often used interchangeably.
A data type is a term which refers to the kinds of data that variables may "hold" in a programming language. In FORTRAN the data types are INTEGER, REAL, LOGICAL, COMPLEX, and DOUBLE PRECISION. In PL/I there is the data type CHARACTER. The fundamental data type of SNOBOL is the character string and in LISP it is the list (or S-expression). With every programming language there is a set of built-in data types. This means that the language allows variables to name data of that type and provides a set of operations which meaningfully manipulates these variables. Some data types are easy to provide because they are already built into the computer's machine language instruction set. Integer and real arithmetic are examples of this. Other data types require considerably more effort to implement. In some languages, there are features which allow one to construct combinations of the built-in types. In COBOL and PL/I this feature is called a STRUCTURE while in PASCAL it is called a RECORD. However, it is not necessary to have such a mechanism. All of the data structures we will see here can be reasonably built within a conventional programming language.
Data object is a term referring to a set of elements, say D. For example the data object integers refers to D = {0,
The notion of a data structure as distinguished from a data object is that we want to describe not only the set of objects, but the way they are related. Saying this another way, we want to describe the set of operations which may legally be applied to elements of the data object. This implies that we must specify the set of operations and show how they work. For integers we would have the arithmetic operations +, -, *, / and perhaps many others such as mod, ceil, floor, greater than, less than, etc. The data object integers plus a description of how +, -, *, /, etc. behave constitutes a data structure definition.
To be more precise lets examine a modest example. Suppose we want to define the data structure natural number (abbreviated natno) where natno = {0,1,2,3, ...} with the three operations being a test for zero addition and equality. The following notation can be used:
In the declare statement five functions are defined by giving their names, inputs and outputs. ZERO is a constant function which means it takes no input arguments and its result is the natural number zero, written as ZERO. ISZERO is a boolean function whose result is either true or false. SUCC stands for successor. Using ZERO and SUCC we can define all of the natural numbers as: ZERO, l = SUCC(ZERO), 2 = SUCC(SUCC(ZERO)), 3 = SUCC(SUCC(SUCC(ZERO))), ... etc. The rules on line 8 tell us exactly how the addition operation works. For example if we wanted to add two and three we would get the following sequence of expressions:
ADD(SUCC(SUCC(ZERO)),SUCC(SUCC(SUCC(ZERO))))
which, by line 8 equals
SUCC(ADD(SUCC(ZERO),SUCC(SUCC(SUCC(ZERO)))))
which, by line 8 equals
SUCC(SUCC(ADD(ZERO,SUCC(SUCC(SUCC(ZERO))))))
which by line 8 equals
SUCC(SUCC(SUCC(SUCC(SUCC(ZERO)))))
Of course, this is not the way to implement addition. In practice we use bit strings which is a data structure that is usually provided on our computers. But however the ADD operation is implemented, it must obey these rules. Hopefully, this motivates the following definition.
Definition: A data structure is a set of domains
In the previous example
The set of axioms describes the semantics of the operations. The form in which we choose to write the axioms is important. Our goal here is to write the axioms in a representation independent way. Then, we discuss ways of implementing the functions using a conventional programming language.
An implementation of a data structure d is a mapping from d to a set of other data structures e. This mapping specifies how every object of d is to be represented by the objects of e. Secondly, it requires that every function of d must be written using the functions of the implementing data structures e. Thus we say that integers are represented by bit strings, boolean is represented by zero and one, an array is represented by a set of consecutive words in memory.
In current parlance the triple
The choice of an algorithm description language must be carefully made because it plays such an important role throughout the book. We might begin by considering using some existing language; some names which come immediately to mind are ALGOL, ALGOL-W, APL, COBOL, FORTRAN, LISP, PASCAL, PL/I, SNOBOL.
Though some of these are more preferable than others, the choice of a specific language leaves us with many difficulties. First of all, we wish to be able to write our algorithms without dwelling on the idiosyncracies of a given language. Secondly, some languages have already provided the mechanisms we wish to discuss. Thus we would have to make pretense to build up a capability which already exists. Finally, each language has its followers and its detractors. We would rather not have any individual rule us out simply because he did not know or, more particularly, disliked to use the language X.
Furthermore it is not really necessary to write programs in a language for which a compiler exists. Instead we choose to use a language which is tailored to describing the algorithms we want to write. Using it we will not have to define many aspects of a language that we will never use here. Most importantly, the language we use will be close enough to many of the languages mentioned before so that a hand translation will be relatively easy to accomplish. Moreover, one can easily program a translator using some existing, but more primitive higher level language as the output (see Appendix A). We call our language SPARKS. Figure 1.2 shows how a SPARKS program could be executed on any machine.
Many language designers choose a name which is an acronym. But SPARKS was not devised in that way; it just appeared one day as Athena sprang from the head of Zeus. Nevertheless, computerniks still try to attach a meaning. Several cute ideas have been suggested, such as
Structured Programming: A Reasonably Komplete Set
or
Smart Programmers Are Required To Know SPARKS.
SPARKS contains facilities to manipulate numbers, boolean values and characters. The way to assign values is by the assignment statement
variable
In addition to the assignment statement, SPARKS includes statements for conditional testing, iteration, input-output, etc. Several such statements can be combined on a single line if they are separated by a semi-colon. Expressions can be either arithmetic, boolean or of character type. In the boolean case there can be only one of two values,
true or false.
In order to produce these values, the logical operators
and, or, not
are provided, plus the relational operators
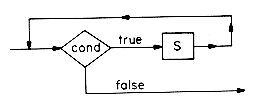
A conditional statement has the form
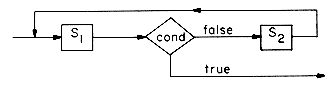
where cond is a boolean expression and S1, S2 are arbitrary groups of SPARKS statements. If S1 or S2 contains more than one statement, these will be enclosed in square brackets. Brackets must be used to show how each else corresponds to one if. The meaning of this statement is given by the flow charts:
We will assume that conditional expressions are evaluated in "short circuit" mode; given the boolean expression (cond1 or cond2), if condl is true then cond2 is not evaluated; or, given (condl and cond2), if cond1 is false then cond2 is not evaluated.
To accomplish iteration, several statements are available. One of them is
where cond is as before, S is as S1 before and the meaning is given by
It is well known that all "proper" programs can be written using only the assignment, conditional and while statements. This result was obtained by Bohm and Jacopini. Though this is very interesting from a theoretical viewpoint, we should not take it to mean that this is the way to program. On the contrary, the more expressive our languages are, the more we can accomplish easily. So we will provide other statements such as a second iteration statement, the repeat-until,
which has the meaning
In contrast to the while statement, the repeat-until guarantees that the statements of S will be executed at least once. Another iteration statement is
which has the meaning
As it stands, this describes an infinite loop! However, we assume that this statement is used in conjunction with some test within S which will cause an exit. One way of exiting such a loop is by using a
go to label
statement which transfers control to "label." Label may be anywhere in the procedure. A more restricted form of the go to is the command
exit
which will cause a transfer of control to the first statement after the innermost loop which contains it. This looping statement may be a while, repeat, for or a loop-forever. exit can be used either conditionally or unconditionally, for instance
which will execute as
The last statement for iteration is called the for-loop, which has the form
Vble is a variable, while start, finish and increment are arithmetic expressions. A variable or a constant is a simple form of an expression. The clause "by increment" is optional and taken as +1 if it does not occur. We can write the meaning of this statement in SPARKS as
Another statement within SPARKS is the case, which allows one to distinguish easily between several alternatives without using multiple if-then-else statements. It has the form
where the Si, 1
The else clause is optional.
A complete SPARKS procedure has the form
A procedure can be used as a function by using the statement
return (expr)
where the value of expr is delivered as the value of the procedure. The expr may be omitted in which case a return is made to the calling procedure. The execution of an end at the end of procedure implies a return. A procedure may be invoked by using a call statement
call NAME (parameter list)
Procedures may call themselves, direct recursion, or there may be a sequence resulting in indirect recursion. Though recursion often carries with it a severe penalty at execution time, it remains all elegant way to describe many computing processes. This penalty will not deter us from using recursion. Many such programs are easily translatable so that the recursion is removed and efficiency achieved.
A complete SPARKS program is a collection of one or more procedures, the first one taken as the main program. All procedures are treated as external, which means that the only means for communication between them is via parameters. This may be somewhat restrictive in practice, but for the purpose of exposition it helps to list all variables explicitly, as either local or parameter. The association of actual to formal parameters will be handled using the call by reference rule. This means that at run time the address of each parameter is passed to the called procedure. Parameters which are constants or values of expressions are stored into internally generated words whose addresses are then passed to the procedure.
For input/output we assume the existence of two functions
read (argument list), print (argument list)
Arguments may be variables or quoted strings. We avoid the problem of defining a "format" statement as we will need only the simplest form of input and output.
The command stop halts execution of the currently executing procedure. Comments may appear anywhere on a line enclosed by double slashes, e.g.
//this is a comment//
Finally, we note that multi-dimensional arrays are available with arbitrary integer lower and upper bounds. An n-dimensional array A with lower and upper bounds li, ui, 1
Since most of the SPARKS programs will be read many more times than they will be executed, we have tried to make the code readable. This is a goal which should be aimed at by everyone who writes programs. The SPARKS language is rich enough so that one can create a good looking program by applying some simple rules of style.
(i) Every procedure should carefully specify its input and output variables.
(ii) The meaning of variables should be defined.
(iii) The flow of the program should generally be forward except for normal looping or unavoidable instances.
(iv) Indentation rules should be established and followed so that computational units of program text can more easily be identified.
(v) Documentation should be short, but meaningful. Avoid sentences like ''i is increased by one."
(vi) Use subroutines where appropriate.
See the book The Elements of Programming Style by Kernighan and Plauger for more examples of good rules of programming.
Now that you have moved beyond the first course in computer science, you should be capable of developing your programs using something better than the seat-of-the-pants method. This method uses the philosophy: write something down and then try to get it working. Surprisingly, this method is in wide use today, with the result that an average programmer on an average job turns out only between five to ten lines of correct code per day. We hope your productivity will be greater. But to improve requires that you apply some discipline to the process of creating programs. To understand this process better, we consider it as broken up into five phases: requirements, design, analysis, coding, and verification.
(i) Requirements. Make sure you understand the information you are given (the input) and what results you are to produce (the output). Try to write down a rigorous description of the input and output which covers all cases.
You are now ready to proceed to the design phase. Designing an algorithm is a task which can be done independently of the programming language you eventually plan to use. In fact, this is desirable because it means you can postpone questions concerning how to represent your data and what a particular statement looks like and concentrate on the order of processing.
(ii) Design. You may have several data objects (such as a maze, a polynomial, or a list of names). For each object there will be some basic operations to perform on it (such as print the maze, add two polynomials, or find a name in the list). Assume that these operations already exist in the form of procedures and write an algorithm which solves the problem according to the requirements. Use a notation which is natural to the way you wish to describe the order of processing.
(iii) Analysis. Can you think of another algorithm? If so, write it down. Next, try to compare these two methods. It may already be possible to tell if one will be more desirable than the other. If you can't distinguish between the two, choose one to work on for now and we will return to the second version later.
(iv) Refinement and coding. You must now choose representations for your data objects (a maze as a two dimensional array of zeros and ones, a polynomial as a one dimensional array of degree and coefficients, a list of names possibly as an array) and write algorithms for each of the operations on these objects. The order in which you do this may be crucial, because once you choose a representation, the resulting algorithms may be inefficient. Modern pedagogy suggests that all processing which is independent of the data representation be written out first. By postponing the choice of how the data is stored we can try to isolate what operations depend upon the choice of data representation. You should consider alternatives, note them down and review them later. Finally you produce a complete version of your first program.
It is often at this point that one realizes that a much better program could have been built. Perhaps you should have chosen the second design alternative or perhaps you have spoken to a friend who has done it better. This happens to industrial programmers as well. If you have been careful about keeping track of your previous work it may not be too difficult to make changes. One of the criteria of a good design is that it can absorb changes relatively easily. It is usually hard to decide whether to sacrifice this first attempt and begin again or just continue to get the first version working. Different situations call for different decisions, but we suggest you eliminate the idea of working on both at the same time. If you do decide to scrap your work and begin again, you can take comfort in the fact that it will probably be easier the second time. In fact you may save as much debugging time later on by doing a new version now. This is a phenomenon which has been observed in practice.
The graph in figure 1.3 shows the time it took for the same group to build 3 FORTRAN compilers (A, B and C). For each compiler there is the time they estimated it would take them and the time it actually took. For each subsequent compiler their estimates became closer to the truth, but in every case they underestimated. Unwarrented optimism is a familiar disease in computing. But prior experience is definitely helpful and the time to build the third compiler was less than one fifth that for the first one.
(v) Verification. Verification consists of three distinct aspects: program proving, testing and debugging. Each of these is an art in itself. Before executing your program you should attempt to prove it is correct. Proofs about programs are really no different from any other kinds of proofs, only the subject matter is different. If a correct proof can be obtained, then one is assured that for all possible combinations of inputs, the program and its specification agree. Testing is the art of creating sample data upon which to run your program. If the program fails to respond correctly then debugging is needed to determine what went wrong and how to correct it. One proof tells us more than any finite amount of testing, but proofs can be hard to obtain. Many times during the proving process errors are discovered in the code. The proof can't be completed until these are changed. This is another use of program proving, namely as a methodology for discovering errors. Finally there may be tools available at your computing center to aid in the testing process. One such tool instruments your source code and then tells you for every data set: (i) the number of times a statement was executed, (ii) the number of times a branch was taken, (iii) the smallest and largest values of all variables. As a minimal requirement, the test data you construct should force every statement to execute and every condition to assume the value true and false at least once.
One thing you have forgotten to do is to document. But why bother to document until the program is entirely finished and correct ? Because for each procedure you made some assumptions about its input and output. If you have written more than a few procedures, then you have already begun to forget what those assumptions were. If you note them down with the code, the problem of getting the procedures to work together will be easier to solve. The larger the software, the more crucial is the need for documentation.
The previous discussion applies to the construction of a single procedure as well as to the writing of a large software system. Let us concentrate for a while on the question of developing a single procedure which solves a specific task. This shifts our emphasis away from the management and integration of the various procedures to the disciplined formulation of a single, reasonably small and well-defined task. The design process consists essentially of taking a proposed solution and successively refining it until an executable program is achieved. The initial solution may be expressed in English or some form of mathematical notation. At this level the formulation is said to be abstract because it contains no details regarding how the objects will be represented and manipulated in a computer. If possible the designer attempts to partition the solution into logical subtasks. Each subtask is similarly decomposed until all tasks are expressed within a programming language. This method of design is called the top-down approach. Inversely, the designer might choose to solve different parts of the problem directly in his programming language and then combine these pieces into a complete program. This is referred to as the bottom-up approach. Experience suggests that the top-down approach should be followed when creating a program. However, in practice it is not necessary to unswervingly follow the method. A look ahead to problems which may arise later is often useful.
Underlying all of these strategies is the assumption that a language exists for adequately describing the processing of data at several abstract levels. For this purpose we use the language SPARKS coupled with carefully chosen English narrative. Such an algorithm might be called pseudo-SPARKS. Let us examine two examples of top-down program development.
Suppose we devise a program for sorting a set of n
"from those integers which remain unsorted, find the smallest and place it next in the sorted list"
This statement is sufficient to construct a sorting program. However, several issues are not fully specified such as where and how the integers are initially stored and where the result is to be placed. One solution is to store the values in an array in such a way that the i-th integer is stored in the i-th array position, A(i) 1
Note how we have begun to use SPARKS pseudo-code. There now remain two clearly defined subtasks: (i) to find the minimum integer and (ii) to interchange it with A(i). This latter problem can be solved by the code
t
The first subtask can be solved by assuming the minimum is A (i), checking A(i) with A(i + 1), A(i + 2), ... and whenever a smaller element is found, regarding it as the new minimum. Eventually A(n) is compared to the current minimum and we are done. Putting all these observations together we get
The obvious question to ask at this point is: "does this program work correctly?"
Theorem: Procedure SORT (A,n) correctly sorts a set of n
Proof: We first note that for any i, say i = q, following the execution of lines 2 thru 6, it is the case that A(q)
We observe at this point that the upper limit of the for-loop in line 1 can be changed to n - 1 without damaging the correctness of the algorithm.
From the standpoint of readability we can ask if this program is good. Is there a more concise way of describing this algorithm which will still be as easy to comprehend? Substituting while statements for the for loops doesn't significantly change anything. Also, extra initialization and increment statements would be required. We might consider a FORTRAN version using the ANSI language standard
FORTRAN forces us to clutter up our algorithms with extra statements. The test for N = 1 is necessary because FORTRAN DO-LOOPS always insist on executing once. Variables NM1 and JP1 are needed because of the restrictions on lower and upper limits of DO-LOOPS.
Let us develop another program. We assume that we have n
"let A(mid) be the middle element. There are three possibilities. Either x < A(mid) in which case x can only occur as A(1) to A(mid - 1); or x > A(mid) in which case x can only occur as A(mid + l) to A(n): or x = A(mid) in which case set j to mid and return. Continue in this way by keeping two pointers, lower and upper, to indicate the range of elements not yet tested."
At this point you might try the method out on some sample numbers. This method is referred to as binary search. Note how at each stage the number of elements in the remaining set is decreased by about one half. We can now attempt a version using SPARKS pseudo code.
The above is not the only way we might write this program. For instance we could replace the while loop by a repeat-until statement with the same English condition. In fact there are at least six different binary search programs that can be produced which are all correct. There are many more that we might produce which would be incorrect. Part of the freedom comes from the initialization step. Whichever version we choose, we must be sure we understand the relationships between the variables. Below is one complete version.
To prove this program correct we make assertions about the relationship between variables before and after the while loop of steps 2-9. As we enter this loop and as long as x is not found the following holds:
lower
Now, if control passes out of the while loop past line 9 then we know the condition of line 2 is false
lower > upper.
This, combined with the above assertion implies that x is not present.
Unfortunately a complete proof takes us beyond our scope but for those who wish to pursue program proving they should consult our references at the end of this chapter. An analysis of the computing time for BINSRCH is carried out in section 7.1.
We have tried to emphasize the need to structure a program to make it easier to achieve the goals of readability and correctness. Actually one of the most useful syntactical features for accomplishing this is the procedure. Given a set of instructions which perform a logical operation, perhaps a very complex and long operation, they can be grouped together as a procedure. The procedure name and its parameters are viewed as a new instruction which can be used in other programs. Given the input-output specifications of a procedure, we don't even have to know how the task is accomplished, only that it is available. This view of the procedure implies that it is invoked, executed and returns control to the appropriate place in the calling procedure. What this fails to stress is the fact that procedures may call themselves (direct recursion) before they are done or they may call other procedures which again invoke the calling procedure (indirect recursion). These recursive mechanisms are extremely powerful, but even more importantly, many times they can express an otherwise complex process very clearly. For these reasons we introduce recursion here.
Most students of computer science view recursion as a somewhat mystical technique which only is useful for some very special class of problems (such as computing factorials or Ackermann's function). This is unfortunate because any program that can be written using assignment, the if-then-else statement and the while statement can also be written using assignment, if-then-else and recursion. Of course, this does not say that the resulting program will necessarily be easier to understand. However, there are many instances when this will be the case. When is recursion an appropriate mechanism for algorithm exposition? One instance is when the problem itself is recursively defined. Factorial fits this category, also binomial coefficients where
can be recursively computed by the formula
Another example is reversing a character string, S = 'x1 ... xn' where SUBSTRING (S,i,j) is a function which returns the string xi ... xj for appropriately defined i and j and S
If this looks too simple let us develop a more complex recursive procedure. Given a set of n
(i) a followed by all permutations of (b,c,d)
(ii) b followed by all permutations of (a,c,d)
(iii) c followed by all permutations of (b,a,d)
(iv) d followed by all permutations of (b,c,a)
The expression "followed by all permutations" is the clue to recursion. It implies that we can solve the problem for a set with n elements if we had an algorithm which worked on n - 1 elements. These considerations lead to the following procedure which is invoked by call PERM(A,1,n). A is a character string e.g. A ='abcd', and INTERCHANGE (A,k,i) exchanges the k-th character of A with the i-th character of A.
Try this algorithm out on sets of length one, two, and three to insure that you understand how it works. Then try to do one or more of the exercises at the end of this chapter which ask for recursive procedures.
Another time when recursion is useful is when the data structure that the algorithm is to operate on is recursively defined. We will see several important examples of such structures, especially lists in section 4.9 and binary trees in section 5.4. Another instance when recursion is invaluable is when we want to describe a backtracking procedure. But for now we will content ourselves with examining some simple, iterative programs and show how to eliminate the iteration statements and replace them by recursion. This may sound strange, but the objective is not to show that the result is simpler to understand nor more efficient to execute. The main purpose is to make one more familiar with the execution of a recursive procedure.
Suppose we start with the sorting algorithm presented in this section. To rewrite it recursively the first thing we do is to remove the for loops and express the algorithm using assignment, if-then-else and the go-to statement.
Now every place where we have a label we introduce a procedure whose parameters are the variables which are already assigned a value at that point. Every place where a ''go to label'' appears, we replace that statement by a call of the procedure associated with that label. This gives us the following set of three procedures.
We can simplify these procedures somewhat by ignoring SORT(A,n) entirely and begin the sorting operation by call SORTL1(A,n,1). Notice how SORTL1 is directly recursive while it also uses procedure MAXL2. Procedure MAXL2 is also directly reculsive. These two procedures use eleven lines while the original iterative version was expressed in nine lines; not much of a difference. Notice how in MAXL2 the fourth parameter k is being changed. The effect of increasing k by one and restarting the procedure has essentially the same effect as the for loop.
Now let us trace the action of these procedures as they sort a set of five integers
When a procedure is invoked an implicit branch to its beginning is made. Thus a recursive call of a program can be made to simulate a go to statement. The parameter mechanism of the procedure is a form of assignment. Thus placing the argument k + 1 as the fourth parameter of MAXL2 is equivalent to the statement k
In section 4.9 we will see the first example of a recursive data structure, the list. Also in that section are several recursive procedures, followed in some cases by their iterative equivalents. Rules are also given there for eliminating recursion.
One goal of this book is to develop skills for making evaluative judgements about programs. There are many criteria upon which we can judge a program, for instance:
(i) Does it do what we want it to do?
(ii) Does it work correctly according to the original specifications of the task?
(iii) Is there documentation which describes how to use it and how it works?
(iv) Are subroutines created in such a way that they perform logical sub-functions?
(v) Is the code readable?
The above criteria are all vitally important when it comes to writing software, most especially for large systems. Though we will not be discussing how to reach these goals, we will try to achieve them throughout this book with the programs we write. Hopefully this more subtle approach will gradually infect your own program writing habits so that you will automatically strive to achieve these goals.
There are other criteria for judging programs which have a more direct relationship to performance. These have to do with computing time and storage requirements of the algorithms. Performance evaluation can be loosely divided into 2 major phases: (a) a priori estimates and (b) a posteriori testing. Both of these are equally important.
First consider a priori estimation. Suppose that somewhere in one of your programs is the statement
x
We would like to determine two numbers for this statement. The first is the amount of time a single execution will take; the second is the number of times it is executed. The product of these numbers will be the total time taken by this statement. The second statistic is called the frequency count, and this may vary from data set to data set. One of the hardest tasks in estimating frequency counts is to choose adequate samples of data. It is impossible to determine exactly how much time it takes to execute any command unless we have the following information:
(i) the machine we are executing on:
(ii) its machine language instruction set;
(iii) the time required by each machine instruction;
(iv) the translation a compiler will make from the source to the machine language.
It is possible to determine these figures by choosing a real machine and an existing compiler. Another approach would be to define a hypothetical machine (with imaginary execution times), but make the times reasonably close to those of existing hardware so that resulting figures would be representative. Neither of these alternatives seems attractive. In both cases the exact times we would determine would not apply to many machines or to any machine. Also, there would be the problem of the compiler, which could vary from machine to machine. Moreover, it is often difficult to get reliable timing figures because of clock limitations and a multi-programming or time sharing environment. Finally, the difficulty of learning another machine language outweighs the advantage of finding "exact" fictitious times. All these considerations lead us to limit our goals for an a priori analysis. Instead, we will concentrate on developing only the frequency count for all statements. The anomalies of machine configuration and language will be lumped together when we do our experimental studies. Parallelism will not be considered.
Consider the three examples of Figure 1.4 below.
In program (a) we assume that the statement x
To determine the order of magnitude, formulas such as
often occur. In the program segment of figure 1.4(c) the statement x
Simple forms for the above three formulas are well known, namely,
In general
To clarify some of these ideas, let us look at a simple program for computing the n-th Fibonacci number. The Fibonacci sequence starts as
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Each new term is obtained by taking the sum of the two previous terms. If we call the first term of the sequence F0 then F0 = 0, F1 = 1 and in general
Fn = Fn-1 + Fn-2, n
The program on the following page takes any non-negative integer n and prints the value Fn.
The first problem in beginning an analysis is to determine some reasonable values of n. A complete set would include four cases: n < 0, n = 0, n = 1 and n > 1. Below is a table which summarizes the frequency counts for the first three cases.
These three cases are not very interesting. None of them exercises the program very much. Notice, though, how each if statement has two parts: the if condition and the then clause. These may have different execution counts. The most interesting case for analysis comes when n > 1. At this point the for loop will actually be entered. Steps 1, 2, 3, 5, 7 and 9 will be executed once, but steps 4, 6 and 8 not at all. Both commands in step 9 are executed once. Now, for n
Each statement is counted once, so step 9 has 2 statements and is executed once for a total of 2. Clearly, the actual time taken by each statement will vary. The for statement is really a combination of several statements, but we will count it as one. The total count then is 5n + 5. We will often write this as O(n), ignoring the two constants 5. This notation means that the order of magnitude is proportional to n.
The notation f(n) = O(g(n)) (read as f of n equals big-oh of g of n) has a precise mathematical definition.
Definition: f(n) = O(g(n)) iff there exist two constants c and no such that |f(n)|
f(n) will normally represent the computing time of some algorithm. When we say that the computing time of an algorithm is O(g(n)) we mean that its execution takes no more than a constant times g(n). n is a parameter which characterizes the inputs and/or outputs. For example n might be the number of inputs or the number of outputs or their sum or the magnitude of one of them. For the Fibonacci program n represents the magnitude of the input and the time for this program is written as T(FIBONACCI) = O(n).
We write O(1) to mean a computing time which is a constant. O(n) is called linear, O(n2) is called quadratic, O(n3) is called cubic, and O(2n) is called exponential. If an algorithm takes time O(log n) it is faster, for sufficiently large n, than if it had taken O(n). Similarly, O(n log n) is better than O(n2) but not as good as O(n). These seven computing times, O(1), O(log n), O(n), O(n log n), O(n2), O(n3), and O(2n) are the ones we will see most often throughout the book.
If we have two algorithms which perform the same task, and the first has a computing time which is O(n) and the second O(n2), then we will usually take the first as superior. The reason for this is that as n increases the time for the second algorithm will get far worse than the time for the first. For example, if the constant for algorithms one and two are 10 and 1/2 respectively, then we get the following table of computing times:
For n
Figures 1.6 and 1.7 show how the computing times (counts) grow with a constant equal to one. Notice how the times O(n) and O(n log n) grow much more slowly than the others. For large data sets, algorithms with a complexity greater than O(n log n) are often impractical. An algorithm which is exponential will work only for very small inputs. For exponential algorithms, even if we improve the constant, say by 1/2 or 1/3, we will not improve the amount of data we can handle by very much.
Given an algorithm, we analyze the frequency count of each statement and total the sum. This may give a polynomial
P(n) = cknk + ck-1 nk-1 + ... + c1n + co
where the ci are constants, ck
c2n + P(n) = O(2n).
Another valid performance measure of an algorithm is the space it requires. Often one can trade space for time, getting a faster algorithm but using more space. We will see cases of this in subsequent chapters.
We end this chapter with a problem from recreational mathematics which uses many of the SPARKS features that have been discussed. A magic square is an n x n matrix of the integers 1 to n2 such that the sum of every row, column and diagonal is the same. For example, if n = 5 we have
where the common sum is 65. When n is odd H. Coxeter has given a simple rule for generating a magic square:
"Start with 1 in the middle of the top row; then go up and left assigning numbers in increasing order to empty squares; if you fall off the square imagine the same square as tiling the plane and continue; if a square is occupied, move down instead and continue."
The magic square above was formed using this rule. We now write a SPARKS program for creating an n X n magic square for n odd.
MAGIC is a complete SPARKS procedure. The statement (i,j)
The while loop is governed by the variable key which is an integer variable initialized to 2 and increased by one each time through the loop. Thus each statement within the while loop will be executed no more than n2 - 1 times and hence the computing time for MAGIC is O(n2). Since there are n2 positions in which the algorithm must place a number, we see that O(n2) is the best bound an algorithm could have.
For a discussion of algorithms and how to analyze them see
The Art of Computer Programming: Fundamental Algorithms, by D. E. Knuth, vol. 1, chapter 1, 2-nd edition, Addison-Wesley, 1973.
For a discussion of good programming techniques see
Structured Programming by O. J. Dahl, E. W. Dijkstra, and C. A. R. Hoare, Academic Press, 1972.
The Elements of Programming Style by B. W. Kernighan and P. J. Plauger, McGraw-Hill, 1974.
ACM Computing Surveys, Special Issue: Programming, vol. 6, no. 4, December, 1974.
For a discussion of tools and procedures for developing very large software systems see
Practical Strategies for Developing Large Software Systems, by E. Horowitz, Addison-Wesley, May, 1975.
For a discussion of the more abstract formulation of data structures see
"Toward an understanding of data structures" by J. Earley, CACM, vol. 14, no. 10, October, 1971, pp. 617-627.
"Another look at data," by G. Mealy, Proc. AFIPS Fall Joint Computer Conference, vol. 31, 1967, pp. 525-534.
For a further discussion of program proving see
"Assigning meaning to programs," by R. W. Floyd, Proc. of a Symposium in Applied Mathematics, vol. 19, J. T. Schwartz, ed., American Mathematical Society, Providence, 1967, pp. 19-32.
"An interactive program verification system," by D. I. Good, R. L. London, W. W. Bledsoe, IEEE Transactions on Software Engineering, SE-1, vol. 1, March, 1975, pp. 59-67.
1. Look up the word algorithm or its older form algorism in the dictionary.
2. Consider the two statements: (i) Is n = 2 the largest value of n for which there exists positive integers x, y and z such that xn + yn = zn has a solution; (ii) Store 5 divided by zero into X and go to statement 10. Both do not satisfy one of the five criteria of an algorithm. Which criteria do they violate?
3. Describe the flowchart in figure 1.1 by using a combination of SPARKS and English. Can you do this without using the go to? Now make it into an algorithm.
4. Discuss how you would actually represent the list of name and telephone number pairs in a real machine. How would you handle people with the same last name.
5. Write FORTRAN equivalents of the while, repeat-until, loop-forever and for statements of SPARKS.
6. Can you think of a clever meaning for S.P.A.R.K.S.? Concentrate on the letter K first.
7. Determine the frequency counts for all statements in the following two SPARKS program segments:
8. Horner's Rule is a means for evaluating a polynomial A(x) = anxn + an-1xn-1 + ... +a1 x + a0 at a point x0 using a minimum number of multiplications. The rule is:
A(x) = (... ((an.x0 + an-1)x0 + ... + a1)x0 + a0
Write a SPARKS program to evaluate a polynomial using Horner's Rule. Determine how many times each statement is executed.
9. Given n boolean variables x1,..., xn we wish to print all possible combinations of truth values they can assume. For instance, if n = 2, there are four possibilities: true, true; true, false; false, true; false, false. Write a SPARKS program to accomplish this and do a frequency count.
10. Compare the two functions n2 and 2n/4 for various values of n. Determine when the second becomes larger than the first.
11. Write a SPARKS program which prints out the integer values of x, y, z in nondecreasing order. What is the computing time of your method?
12. Write a SPARKS procedure which searches an array A (1: n) for the element x. If x occurs, then set j to its position in the array else set j to zero. Try writing this without using the go to statement.
13. One useful facility we might add to SPARKS is the ability to manipulate character strings. If x, y are variables of type character, then we might like to implement the procedures:
(i) z
(ii) z
(iii) z
Implement these procedures using the array facility.
14. Write a SPARKS procedure which is given an argument STRING, whose value is a character string of length n. Copy STRING into the variable FILE so that every sequence of blanks is reduced to a single blank. The last character of STRING is nonblank.
15. Design a program that counts the number of occurrences of each character in the string STRING of length n. Represent your answer in the array ANS(1:k,1:2) where ANS(i,l) is the i-th character and ANS(i,2) is the number of times it occurs in STRING.
16. Trace the action of the procedure below on the elements 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 searching for l, 3, 13 and 21.
What is the computing time for this segment in terms of n?
17. Prove by induction:
18. List as many rules of style in programming that you can think of that you would be willing to follow yourself.
19. Using the notation introduced at the end of section 1.1, define the structure Boolean with operations AND, OR, NOT, IMP and EQV (equivalent) using only the if-then-else statement. e.g. NOT (X) :: = if X then false else true.
20. Give a version of a binary search procedure which initializes lower to zero and upper to n + l.
21. Take any version of binary search, express it using assignment, if-then-else and go to and then give an equivalent recursive program.
22. Analyze the computing time of procedure SORT as given in section 1.3.
23. Write a recursive procedure for computing the binomial coefficient
24. Ackermann's function A(m,n) is defined as follows:
This function is studied because it grows very fast for small values of m and n. Write a recursive procedure for computing this function. Then write a nonrecursive algorithm for computing Ackermann's function.
25. (Tower of Hanoi) There are three towers and sixty four disks of different diameters placed on the first tower. The disks are in order of decreasing diameter as one scans up the tower. Monks were reputedly supposed to move the disks from tower 1 to tower 3 obeying the rules: (i) only one disk can be moved at any time; (ii) no disk can be placed on top of a disk with smaller diameter. Write a recursive procedure which prints the sequence of moves which accomplish this task.
26. Write an equivalent recursive version of procedure MAGIC as given in section 1.4.
27. The pigeon hole principle states that if a function f has n distinct inputs but less than n distinct outputs then there exists two inputs a, b such that a
28. Given n, a positive integer determine if n is the sum of all of its divisors; i.e. if n is the sum of all t such that 1
29. Consider the function F(x) defined by
F(x)
Prove that F(x) terminates for all integers x. (Hint: consider integers of the form (2i + 1) 2k - 1 and use induction.)
30. If S is a set of n elements the powerset of S is the set of all possible subsets of S. For example if S = (a,b,c,) then POWERSET(S) = {( ), (a), (b), (c), (a,b), (a,c), (b,c), (a,b,c)}. Write a recursive procedure to compute powerset (S).
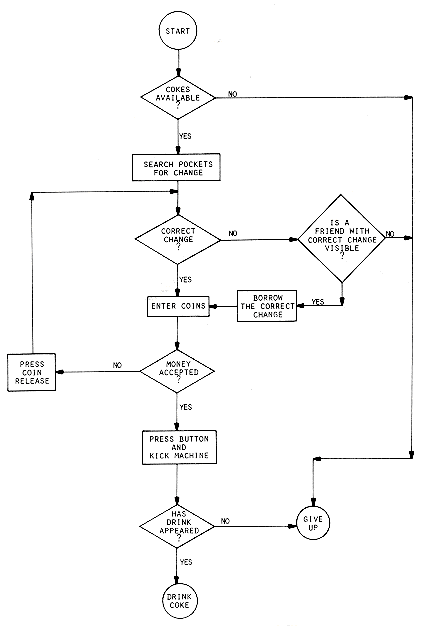
Figure 1.1: Flowchart for obtaining a Coca-Cola
 1,
1,  2, ...}. The data object alphabetic character strings of length less than thirty one implies D = {",'A','B', ...,'Z','AA', ...}. Thus, D may be finite or infinite and if D is very large we may need to devise special ways of representing its elements in our computer.
2, ...}. The data object alphabetic character strings of length less than thirty one implies D = {",'A','B', ...,'Z','AA', ...}. Thus, D may be finite or infinite and if D is very large we may need to devise special ways of representing its elements in our computer.structure NATNO
1 declare ZERO( )
 natno
natno2 ISZERO(natno)
 boolean
boolean3 SUCC(natno)
 natno
natno4 ADD(natno, natno)
 natno
natno5 EQ(natno, natno)
 boolean
boolean6 for all x, y
 natno let
natno let7 ISZERO(ZERO) ::= true; ISZERO(SUCC(x)) ::= false
8 ADD(ZERO, y) :: = y, ADD(SUCC(x), y) :: =
SUCC(ADD(x, y))
9 EQ(x, ZERO) :: = if ISZERO(x) then true else false
10 EQ(ZERO, SUCC(y)) :: = false
EQ(SUCC(x), SUCC(y)) :: = EQ(x, y)
11 end
end NATNO
 , a designated domain
, a designated domain  , a set of functions
, a set of functions  and a set of axioms
and a set of axioms  . The triple
. The triple  denotes the data structure d and it will usually be abbreviated by writing d.
denotes the data structure d and it will usually be abbreviated by writing d.
 is referred to as an abstract data type. It is called abstract precisely because the axioms do not imply a form of representation. Another way of viewing the implementation of a data structure is that it is the process of refining an abstract data type until all of the operations are expressible in terms of directly executable functions. But at the first stage a data structure should be designed so that we know what it does, but not necessarily how it will do it. This division of tasks, called specification and implementation, is useful because it helps to control the complexity of the entire process.
is referred to as an abstract data type. It is called abstract precisely because the axioms do not imply a form of representation. Another way of viewing the implementation of a data structure is that it is the process of refining an abstract data type until all of the operations are expressible in terms of directly executable functions. But at the first stage a data structure should be designed so that we know what it does, but not necessarily how it will do it. This division of tasks, called specification and implementation, is useful because it helps to control the complexity of the entire process.1.2 SPARKS

Figure 1.2: Translation of SPARKS
 expression.
expression.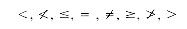
if cond then S1 if cond then S1
or
else S2

while cond do
S
end
repeat
S
until cond

loop
S
forever

loop
S1
if cond then exit
S2
forever
for vble
 start to finish by increment do
start to finish by increment doS
end
vble
 start
startfin
 finish
finishincr
 increment
incrementwhile (vble - fin) * incr
 0 do
0 doS
vble
 vble + incr
vble + incrend
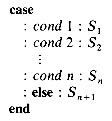
 i
i  n + 1 are groups of SPARKS statements. The semantics is easily described by the following flowchart:
n + 1 are groups of SPARKS statements. The semantics is easily described by the following flowchart: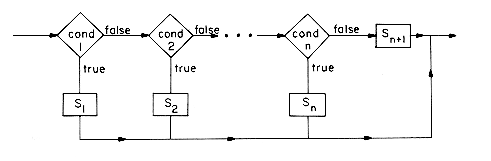
procedure NAME (parameter list)
S
end
 i
i  n may be declared by using the syntax declare A(l1:u1, ...,ln:un). We have avoided introducing the record or structure concept. These are often useful features and when available they should be used. However, we will persist in building up a structure from the more elementary array concept. Finally, we emphasize that all of our variables are assumed to be of type INTEGER unless stated otherwise.
n may be declared by using the syntax declare A(l1:u1, ...,ln:un). We have avoided introducing the record or structure concept. These are often useful features and when available they should be used. However, we will persist in building up a structure from the more elementary array concept. Finally, we emphasize that all of our variables are assumed to be of type INTEGER unless stated otherwise.1.3 HOW TO CREATE PROGRAMS
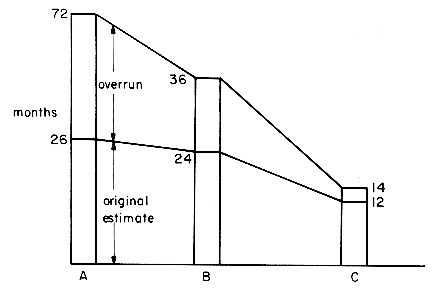
Figure 1.3: History of three FORTRAN compilers
 1 distinct integers. One of the simplest solutions is given by the following
1 distinct integers. One of the simplest solutions is given by the following i
i  n. We are now ready to give a second refinement of the solution:
n. We are now ready to give a second refinement of the solution:for i
 1 to n do
1 to n doexamine A(i) to A(n) and suppose the
smallest integer is at A(j); then
interchange A(i) and A(j).
end
 A(i); A(i)
A(i); A(i)  A(j); A(j)
A(j); A(j)  t
tprocedure SORT(A,n)
1 for i
 1 to n do
1 to n do2 j
 i
i3 for k
 j + 1 to n do
j + 1 to n do4 if A(k) < A(j) then j
 k
k5 end
6 t
 A(i); A(i)
A(i); A(i)  A(j); A(j)
A(j); A(j)  t
t7 end
end SORT
 1 distinct integers, the result remains in A (1:n) such that A (1) < A (2) < ... < A(n).
1 distinct integers, the result remains in A (1:n) such that A (1) < A (2) < ... < A(n). A(r), q < r
A(r), q < r  n. Also, observe that when i becomes greater than q, A(1 .. q) is unchanged. Hence, following the last execution of these lines, (i.e., i = n), we have A(1)
n. Also, observe that when i becomes greater than q, A(1 .. q) is unchanged. Hence, following the last execution of these lines, (i.e., i = n), we have A(1)  A(2)
A(2)  ...
...  A(n).
A(n). IF (N. LE. 1) GO TO 100
NM1 = N - 1
DO 101 I = 1, NM1
J = I
JP1 = J + 1
DO 102 K = JP1, N
IF (A(K).LT.A(J)) J = K
102 CONTINUE
T = A(I)
A(I) = A(J)
A(J) = T
101 CONTINUE
100 CONTINUE
 1 distinct integers which are already sorted and stored in the array A(1:n). Our task is to determine if the integer x is present and if so to return j such that x = A(j); otherwise return j = 0. By making use of the fact that the set is sorted we conceive of the following efficient method:
1 distinct integers which are already sorted and stored in the array A(1:n). Our task is to determine if the integer x is present and if so to return j such that x = A(j); otherwise return j = 0. By making use of the fact that the set is sorted we conceive of the following efficient method:procedure BINSRCH(A,n,x,j)
initialize lower and upper
while there are more elements to check do
let A(mid) be the middle element
case
: x > A(mid): set lower to mid + 1
: x < A(mid): set upper to mid - 1
: else: found
end
end
not found
end BINSRCH
procedure BINSRCH (A,n,x,j)
1 lower
 1; upper
1; upper  n
n 2 while lower
 upper do
upper do 3 mid

 (lower + upper) / 2
(lower + upper) / 2
4 case
5 : x > A(mid): lower
 mid + 1
mid + 1 6 : x < A(mid): upper
 mid - 1
mid - 1 7 : else: j
 mid; return
mid; return 8 end
9 end
10 j
 0
0end
 upper and A (lower)
upper and A (lower)  x
x  A (upper) and SORTED (A, n)
A (upper) and SORTED (A, n)Recursion
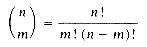


 T stands for concatenation of two strings (as in PL/I). Then the operation REVERSE is easily described recursively as
T stands for concatenation of two strings (as in PL/I). Then the operation REVERSE is easily described recursively asprocedure REVERSE(S)
n
 LENGTH(S)
LENGTH(S)if n = 1 then return (S)
else return (REVERSE(SUBSTRING(S,2,n))

 SUBSTRING(S,1,1))
SUBSTRING(S,1,1))end REVERSE
 1 elements the problem is to print all possible permutations of this set. For example if the set is {a,b,c}, then the set of permutations is {(a, b,c), (a,c,b), (b,a,c), (b,c,a), (c,a,b), (c,b,a)}. It is easy to see that given n elements there are n ! different permutations. A simple algorithm can be achieved by looking at the case of four elements (a,b,c,d). The answer is obtained by printing
1 elements the problem is to print all possible permutations of this set. For example if the set is {a,b,c}, then the set of permutations is {(a, b,c), (a,c,b), (b,a,c), (b,c,a), (c,a,b), (c,b,a)}. It is easy to see that given n elements there are n ! different permutations. A simple algorithm can be achieved by looking at the case of four elements (a,b,c,d). The answer is obtained by printingprocedure PERM(A,k,n)
if k = n then [print (A); return]
B
 A
Afor i
 k to n do
k to n docall INTERCHANGE(A,k,i)
call PERM(A,k + 1,n)
A
 B
Bend
end PERM
procedure SORT(A,n)
i
 1
1Ll: if i
 n - 1 // for i
n - 1 // for i  1 to n - 1 do//
1 to n - 1 do//then [j
 i; k
i; k  j + 1
j + 1L2: if k
 n //for k
n //for k  j + 1 to n do//
j + 1 to n do//then [if A(k) < A(j)
then j
 k
kk
 k + 1; go to L2]
k + 1; go to L2]t
 A(i); A(i)
A(i); A(i)  A(j); A(j)
A(j); A(j)  t
ti
 i + 1; go to L1]
i + 1; go to L1]end SORT
procedure SORT(A,n)
call SORTL1(A,n,1)
end SORT
procedure SORTLl(A,n,i)
if i
 n - 1
n - 1then [j
 i; call MAXL2(A,n,j,i + 1)
i; call MAXL2(A,n,j,i + 1)t
 A(i); A(i)
A(i); A(i)  A(j); A(j)
A(j); A(j)  t
tcall SORTL1(A,n,i + 1)]
end SORTL1
procedure MAXL2(A,n,j,k)
if k
 n
nthen [if A(k) < A(j) then j
 k
kcall MAXL2(A,n,j,k + 1)]
end MAXL2

 k + 1.
k + 1.1.4 HOW TO ANALYZE PROGRAMS
 x + 1.
x + 1. . for i
 1 to n do
1 to n do . for i
 1 to n do
1 to n do . for j
 1 to n do
1 to n dox
 x + l x
x + l x  x + 1
x + 1 . x
 x + 1
x + 1 . end
. end
end
(a) (b) (c)
Figure 1.4: Three simple programs for frequency counting.
 x + 1 is not contained within any loop either explicit or implicit. Then its frequency count is one. In program (b) the same statement will be executed n times and in program (c) n2 times (assuming n
x + 1 is not contained within any loop either explicit or implicit. Then its frequency count is one. In program (b) the same statement will be executed n times and in program (c) n2 times (assuming n  1). Now 1, n, and n2 are said to be different and increasing orders of magnitude just like 1, 10, 100 would be if we let n = 10. In our analysis of execution we will be concerned chiefly with determining the order of magnitude of an algorithm. This means determining those statements which may have the greatest frequency count.
1). Now 1, n, and n2 are said to be different and increasing orders of magnitude just like 1, 10, 100 would be if we let n = 10. In our analysis of execution we will be concerned chiefly with determining the order of magnitude of an algorithm. This means determining those statements which may have the greatest frequency count.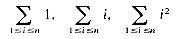
 x + 1 is executed
x + 1 is executed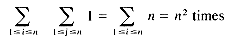
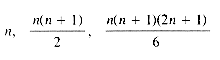
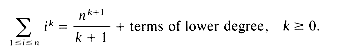
 2.
2.1 procedure FIBONACCI
2 read (n)
3-4 if n < 0 then [print ('error'); stop]5-6 if n = 0 then [print ('0'); stop]7-8 if n = 1 then [print ('1'); stop]9 fnm2
 0; fnm 1
0; fnm 1  1
110 for i
 2 to n do
2 to n do11 fn
 fnm1 + fnm2
fnm1 + fnm212 fnm2
 fnm1
fnm113 fnm1
 fn
fn14 end
15 print (fn)
16 end FIBONACCI
Step n < 0 n = 0 n = 1
--------------------------
1 1 1 1
2 1 1 1
3 1 1 1
4 1 0 0
5 0 1 1
6 0 1 0
7 0 0 1
8 0 0 1
9-15 0 0 0
 2 how often is step 10 executed: not n - 1 but n times. Though 2 to n is only n - 1 executions, remember that there will be a last return to step 10 where i is incremented to n + 1, the test i > n made and the branch taken to step 15. Thus, steps 11, 12, 13 and 14 will be executed n - 1 times but step 10 will be done n times. We can summarize all of this with a table.
2 how often is step 10 executed: not n - 1 but n times. Though 2 to n is only n - 1 executions, remember that there will be a last return to step 10 where i is incremented to n + 1, the test i > n made and the branch taken to step 15. Thus, steps 11, 12, 13 and 14 will be executed n - 1 times but step 10 will be done n times. We can summarize all of this with a table.Step Frequency Step Frequency
--------------------------------
1 1 9 2
2 1 10 n
3 1 11 n-1
4 0 12 n-1
5 1 13 n-1
6 0 14 n-1
7 1 15 1
8 0 16 1
Figure 1.5: Execution Count for Computing Fn
 c|g(n)| for all n
c|g(n)| for all n  no.
no. n 10n n2/2
-----------------
1 10 1/2
5 50 12-1/2
10 100 50
15 150 112-1/2
20 200 200
25 250 312-1/2
30 300 450
 20, algorithm two had a smaller computing time but once past that point algorithm one became better. This shows why we choose the algorithm with the smaller order of magnitude, but we emphasize that this is not the whole story. For small data sets, the respective constants must be carefully determined. In practice these constants depend on many factors, such as the language and the machine one is using. Thus, we will usually postpone the establishment of the constant until after the program has been written. Then a performance profile can be gathered using real time calculation.
20, algorithm two had a smaller computing time but once past that point algorithm one became better. This shows why we choose the algorithm with the smaller order of magnitude, but we emphasize that this is not the whole story. For small data sets, the respective constants must be carefully determined. In practice these constants depend on many factors, such as the language and the machine one is using. Thus, we will usually postpone the establishment of the constant until after the program has been written. Then a performance profile can be gathered using real time calculation. 0 and n is a parameter. Using big-oh notation, P(n) = O(nk). On the other hand, if any step is executed 2n times or more the expression
0 and n is a parameter. Using big-oh notation, P(n) = O(nk). On the other hand, if any step is executed 2n times or more the expression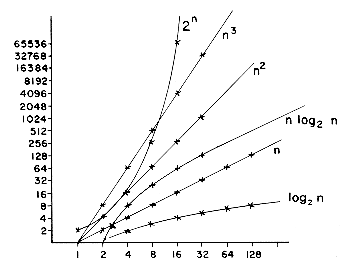
Figure 1.6: Rate of Growth of Common Computing Time Functions
log2n n nlog2n n2 n3 2n
--------------------------------------------------------
0 1 0 1 1 2
1 2 2 4 8 4
2 4 8 16 64 16
3 8 24 64 512 256
4 16 64 256 4096 65536
5 32 160 1024 32768 2, 147, 483, 648
Figure 1.7: Values for Computing Functions
15 8 1 24 17
16 14 7 5 23
22 20 13 6 4
3 21 19 12 10
9 2 25 18 11
procedure MAGIC(square, n)
//for n odd create a magic square which is declared as an array//
//square (0: n - 1, 0: n - 1)//
//(i,j) is a square position. 2
 key
key  n2 is integer valued.//
n2 is integer valued.//if n is even then [print ('input error'); stop]SQUARE
 0
0square (0,(n - 1)/2)
 1; //store 1 in middle of first row//
1; //store 1 in middle of first row//key
 2; i
2; i  0; j
0; j  (n - 1)/2 //i,j are current position//
(n - 1)/2 //i,j are current position//while key
 n2 do
n2 do(k,l)
 ((i - 1) mod n, (j - 1) mod n) //look up and left//
((i - 1) mod n, (j - 1) mod n) //look up and left//if square (k,l)
 0
0then i
 (i + 1) mod n //square occupied, move down//
(i + 1) mod n //square occupied, move down//else (i,j)
 (k,l) //square (k,l) needs to be assigned//
(k,l) //square (k,l) needs to be assigned//square (i,j)
 key //assign it a value//
key //assign it a value//key
 key + 1
key + 1end
print (n, square) //output result//
end MAGIC
 (k,l) is a shorthand way of writing i
(k,l) is a shorthand way of writing i  k; j
k; j  l. It emphasizes that the variables are thought of as pairs and are changed as a unit. The reserved word mod computes the nonnegative remainder and is a built in function. The magic square is represented using a two dimensional array having n rows and n column. For this application it is convenient to number the rows (and columns) from zero to n - 1 rather than from one to n. Thus, when the program ''falls off the square'' the mod operator sets i and/or j back to zero or n - 1.
l. It emphasizes that the variables are thought of as pairs and are changed as a unit. The reserved word mod computes the nonnegative remainder and is a built in function. The magic square is represented using a two dimensional array having n rows and n column. For this application it is convenient to number the rows (and columns) from zero to n - 1 rather than from one to n. Thus, when the program ''falls off the square'' the mod operator sets i and/or j back to zero or n - 1.REFERENCES
EXERCISES
1 for i
 1 to n 1 i
1 to n 1 i  1
12 for j
 l to i 2 while i
l to i 2 while i  n do
n do3 for k
 1 to j 3 x
1 to j 3 x  x + 1
x + 14 x
 x + 1 4 i
x + 1 4 i  i +1
i +15 end 5 end
6 end
7 end
(a) (b)
 CONCAT(x,y) which concatenates a copy of string y to the end of a copy of string x and assigns the resulting string to z. Strings x and y remain unchanged.
CONCAT(x,y) which concatenates a copy of string y to the end of a copy of string x and assigns the resulting string to z. Strings x and y remain unchanged. SUBSTR(x,i,j) which copies to z the i-th to the j-th character in string x with appropriate definitions for j = 0, i > j, etc. String x is unchanged.
SUBSTR(x,i,j) which copies to z the i-th to the j-th character in string x with appropriate definitions for j = 0, i > j, etc. String x is unchanged. INDEX(x,y) which searches string x for the first occurrence of string y and sets z to its starting position in x or else zero.
INDEX(x,y) which searches string x for the first occurrence of string y and sets z to its starting position in x or else zero.i
 1; j
1; j  n
nrepeat k
 (i + j)/2
(i + j)/2if A(k)
 x then i
x then i  k + 1
k + 1else j
 k - 1
k - 1until i > j

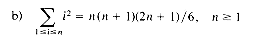
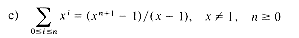
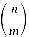 as defined in section 1.3 where
as defined in section 1.3 where  . Analyze the time and space requirements of your algorithm.
. Analyze the time and space requirements of your algorithm.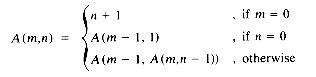
 b and f(a) = f(b). Give an algorithm which finds the values a, b for which the range values are equal.
b and f(a) = f(b). Give an algorithm which finds the values a, b for which the range values are equal. t < n and t divides n.
t < n and t divides n. if even(x) then x/2 else F(F(3x + 1))
if even(x) then x/2 else F(F(3x + 1))


