Since this first application of graphs, they have been used in a wide variety of applications. Some of these applications are: analysis of electrical circuits, finding shortest routes, analysis of project planning, identification of chemical compounds, statistical mechanics, genetics, cybernetics, linguistics, social sciences, etc. Indeed, it might well be said that of all mathematical structures, graphs are the most widely used.

Figure 6.1 Section of the river Pregal in Koenigsberg and Euler's graph.
6.1.2 Definitions and Terminology
A graph, G, consists of two sets V and E. V is a finite non-empty set of vertices. E is a set of pairs of vertices, these pairs are called edges. V(G) and E(G) will represent the sets of vertices and edges of graph G. We will also write G = (V,E) to represent a graph. In an undirected graph the pair of vertices representing any edge is unordered . Thus, the pairs (v1, v2) and (v2, v1) represent the same edge. In a directed graph each edge is represented by a directed pair (v1, v2). v1 is the tail and v2 the head of the edge. Therefore <v2, v1> and <v1, v2> represent two different edges. Figure 6.2 shows three graphs G1, G2 and G3.
The graphs G1 and G2 are undirected. G3 is a directed graph.
V (G1) = {1,2,3,4}; E(G1) = {(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
V (G2) = {1,2,3,4,5,6,7}; E(G2) = {(1,2),(1,3),(2,4),(2,5),(3,6),(3,7)}
V (G3) = {1,2,3}; E(G3) = {<1,2>, <2,1>, <2,3>}.
Note that the edges of a directed graph are drawn with an arrow from the tail to the head. The graph G2 is also a tree while the graphs G1 and G3 are not. Trees can be defined as a special case of graphs, but we need more terminology for that. If (v1,v2) or <v1,v2> is an edge in E(G), then we require v1
The number of distinct unordered pairs (vi,vj) with vi
If (v1,v2) is an edge in E(G), then we shall say the vertices v1 and v2 are adjacent and that the edge (v1,v2) is incident on vertices v1 and v2. The vertices adjacent to vertex 2 in G2 are 4, 5 and 1. The edges incident on vertex 3 in G2 are (1,3), (3,6) and (3,7). If <v1,v2> is a directed edge, then vertex v1 will be said to be adjacent to v2 while v2 is adjacent from v1. The edge <v1,v2> is incident to v1 and v2. In G3 the edges incident to vertex 2 are <1,2>, <2,1> and <2,3>.
A subgraph of G is a graph G' such that V(G')
A path from vertex vp to vertex vq in graph G is a sequence of vertices vp,vi1,vi2, ...,vin,vq such that (vp,vi1),(vi1,vi2), ...,(vin,vq) are edges in E(G). If G' is directed then the path consists of <vp,vi1>,<vi,vi2>, ...,<vin,vq>, edges in E(G'). The length of a path is the number of edges on it. A simple path is a path in which all vertices except possibly the first and last are distinct. A path such as (1,2) (2,4) (4,3) we write as 1,2,4,3. Paths 1,2,4,3 and 1,2,4,2 are both of length 3 in G1. The first is a simple path while the second is not. 1,2,3 is a simple directed path in G3. 1,2,3,2 is not a path in G3 as the edge <3,2> is not in E(G3). A cycle is a simple path in which the first and last vertices are the same. 1,2,3,1 is a cycle in G1. 1,2,1 is a cycle in G3. For the case of directed graphs we normally add on the prefix "directed" to the terms cycle and path. In an undirected graph, G, two vertices v1 and v2 are said to be connected if there is a path in G from v1 to v2 (since G is undirected, this means there must also be a path from v2 to v1). An undirected graph is said to be connected if for every pair of distinct vertices vi, vi in V(G) there is a path from vi to vj in G. Graphs G1 and G2 are connected while G4 of figure 6.5 is not. A connected component or simply a component of an undirected graph is a maximal connected subgraph. G4 has two components H1 and H2 (see figure 6.5). A tree is a connected acyclic (i.e., has no cycles) graph . A directed graph G is said to be strongly connected if for every pair of distinct vertices vi, vj in V(G) there is a directed path from vi to vj and also from vj to vi. The graph G3 is not strongly connected as there is no path from v3 to v2. A strongly connected component is a maximal subgraph that is strongly connected. G3 has two strongly connected components.
The degree of a vertex is the number of edges incident to that vertex. The degree of vertex 1 in G1 is 3. In case G is a directed graph, we define the in-degree of a vertex v to be the number of edges for which v is the head. The out-degree is defined to be the number of edges for which v is the tail. Vertex 2 of G3 has in-degree 1, out-degree 2 and degree 3. If di is the degree of vertex i in a graph G with n vertices and e edges, then it is easy to see that e = (1/2)
In the remainder of this chapter we shall refer to a directed graph as a digraph. An undirected graph will sometimes be referred to simply as a graph.
While several representations for graphs are possible, we shall study only the three most commonly used: adjacency matrices, adjacency lists and adjacency multilists. Once again, the choice of a particular representation will depend upon the application one has in mind and the functions one expects to perform on the graph.
Adjacency Matrix
Let G = (V,E) be a graph with n vertices, n
From the adjacency matrix, one may readily determine if there is an edge connecting any two vertices i and j. For an undirected graph the degree of any vertex i is its row sum
Adjacency Lists
In this representation the n rows of the adjacency matrix are represented as n linked lists. There is one list for each vertex in G. The nodes in list i represent the vertices that are adjacent from vertex i. Each node has at least two fields: VERTEX and LINK. The VERTEX fields contain the indices of the vertices adjacent to vertex i. The adjacency lists for G1, G3 and G4 are shown in figure 6.8. Each list has a headnode. The headnodes are sequential providing easy random access to the adjacency list for any particular vertex. In the case of an undirected graph with n vertices and e edges, this representation requires n head nodes and 2e list nodes. Each list node has 2 fields. In terms of the number of bits of storage needed, this count should be multiplied by log n for the head nodes and log n + log e for the list nodes as it takes O(log m) bits to represent a number of value m. Often one can sequentially pack the nodes on the adjacency lists and eliminate the link fields.
The degree of any vertex in an undirected graph may be determined by just counting the number of nodes in its adjacency list. The total number of edges in G may, therefore, be determined in time O(n + e). In the case of a digraph the number of list nodes is only e. The out-degree of any vertex may be determined by counting the number of nodes on its adjacency list. The total number of edges in G can, therefore, be determined in O(n + e). Determining the in-degree of a vertex is a little more complex. In case there is a need to repeatedly access all vertices adjacent to another vertex then it may be worth the effort to keep another set of lists in addition to the adjacency lists. This set of lists, called inverse adjacency lists, will contain one list for each vertex. Each list will contain a node for each vertex adjacent to the vertex it represents (figure 6.9). Alternatively, one could adopt a
simplified version of the list structure used for sparse matrix representation in section 4.6. Each node would now have four fields and would represent one edge. The node structure would be
Figure 6.10 shows the resulting structure for the graph G3 . The headnodes are stored sequentially.
The nodes in the adjacency lists of figure 6.8 were ordered by the indices of the vertices they represented. It is not necessary that lists be ordered in this way and, in general, the vertices may appear in any order. Thus, the adjacency lists of figure 6.11 would be just as valid a representation of G1.
Adjacency Multilists
In the adjacency list representation of an undirected graph each edge (vi,vj) is represented by two entries, one on the list for vi and the
other on the list for vj. As we shall see, in some situations it is necessary to be able to determine the second entry for a particular edge and mark that edge as already having been examined. This can be accomplished easily if the adjacency lists are actually maintained as multilists (i.e., lists in which nodes may be shared among several lists). For each edge there will be exactly one node, but this node will be in two lists, i.e., the adjacency lists for each of the two nodes it is incident to. The node structure now becomes where
M is a one bit mark field that may be used to indicate whether or not the edge has been examined. The storage requirements are the same as for normal adjacency lists except for the addition of the mark bit M. Figure 6.12 shows the adjacency multilists for G1. We shall study multilists in greater detail in Chapter 10.
Sometimes the edges of a graph have weights assigned to them. These weights may represent the distance from one vertex to another or the
cost of going from one vertex to an adjacent vertex. In this case the adjacency matrix entries A(i,j) would keep this information, too. In the case of adjacency lists and multilists this weight information may be kept in the list nodes by including an additional field. A graph with weighted edges is called a network.
Given the root node of a binary tree, one of the most common things one wishes to do is to traverse the tree and visit the nodes in some order. In the chapter on trees, we defined three ways (preorder, inorder, and postorder) for doing this. An analogous problem arises in the case of graphs. Given an undirected graph G = (V,E) and a vertex v in V(G) we are interested in visiting all vertices in G that are reachable from v (i.e., all vertices connected to v). We shall look at two ways of doing this: Depth First Search and Breadth First Search.
Depth first search of an undirected graph proceeds as follows. The start vertex v is visited. Next an unvisited vertex w adjacent to v is selected and a depth first search from w initiated. When a vertex u is reached such that all its adjacent vertices have been visited, we back up to the last vertex visited which has an unvisited vertex w adjacent to it and initiate a depth first seaerch from w. The search terminates when no unvisited vertex can be reached from any of the visited one. This procedure is best described recursively as in
In case G is represented by its adjacency lists then the vertices w adjacent to v can be determined by following a chain of links. Since the algorithm DFS would examine each node in the adjacency lists at most once and there are 2e list nodes, the time to complete the search is O(e). If G is represented by its adjacency matrix, then the time to determine all vertices adjacent to v is O(n). Since at most n vertices are visited, the total time is O(n2).
The graph G of figure 6.13(a) is represented by its adjacency lists as in figure 6.13(b). If a depth first search is initiated from vertex v1, then the vertices of G are visited in the order: v1, v2, v4, v8, v5, v6, v3, v7. One may easily verify that DFS (v1) visits all vertices connected to v1. So, all the vertices visited, together with all edges in G incident to these vertices form a connected component of G.
Starting at vertex v and marking it as visited, breadth first search differs from depth first search in that all unvisited vertices adjacent to v are visited next. Then unvisited vertices adjacent to these vertices are visited and so on. A breadth first search beginning at vertex v1 of the graph in figure 6.13(a) would first visit v1 and then v2 and v3. Next vertices v4, v5, v6 and v7 will be visited and finally v8. Algorithm BFS gives the details.
Each vertex visited gets into the queue exactly once, so the loop forever is iverated at most n times. If an adjacency matrix is used, then the for loop takes O(n) time for each vertex visited. The total time is, therefore, O(n2). In case adjacency lists are used the for loop has a total cost of d1 + ... + dn = O(e) where di = degree (vi). Again, all vertices visited, together with all edges incident to them form a connected component of G.
We now look at two simple applications of graph traversal: (i) finding the components of a graph, and (ii) finding a spanning tree of a connected graph.
If G is an undirected graph, then one can determine whether or not it is connected by simply making a call to either DFS or BFS and then determining if there is any unvisited vertex. The time to do this is O(n2) if adjacency matrices are used and O(e) if adjacency lists are used. A more interesting problem is to determine all the connected components of a graph. These may be obtained by making repeated calls to either DFS(v) or BFS(v), with v a vertex not yet visited. This leads to algorithm COMP which determines all the connected components of G. The algorithm uses DFS. BFS may be used instead if desired.The computing time is not affected.
If G is represented by its adjacency lists, then the total time taken by DFS is O(e). The output can be completed in time O(e) if DFS keeps a list of all newly visited vertices. Since the for loops take O(n) time, the total time to generate all the connected components is O(n + e).
By the definition of a connected component, there is a path between every pair of vertices in the component and there is no path in G from vertex v to w if v and w are in two different components. Hence, if A is the adjacency matrix of an undirected graph (i.e., A is symmetric) then its transitive closure A+ may be determined in O(n2) time by first determining the connected components. A+(i,j) = 1 iff there is a path from vertex i to j. For every pair of distinct vertices in the same component A + (i,j) = 1. On the diagonal A + (i,i) = 1 iff the component containing i has at least 2 vertices. We shall take a closer look at transitive closure in section 6.3.
When the graph G is connected, a depth first or breadth first search starting at any vertex, visits all the vertices in G. In this case the edges of G are partitioned into two sets T (for tree edges) and B (for back edges), where T is the set of edges used or traversed during the search and B the set of remaining edges. The set T may be determined by inserting the statement T
Figure 6.15 shows the spanning trees resulting from a depth first and breadth first search starting at vertex v1 in the graph of figure 6.13. If any of the edges (v,w) in B (the set of back edges) is introduced into the spanning tree T, then a cycle is formed. This cycle consists of the edge (v,w) and all the edges on the path from w to v in T. If the edge (8,7) is introduced into the DFS spanning tree of figure 6.15(a), then the resulting cycle is 8,7,3,6,8.
Spanning trees find application in obtaining an independent set of circuit equations for an electrical network. First, a spanning tree for the network is obtained. Then the edges in B (i.e., edges not in the spanning tree) are introduced one at a time. The introduction of each such edge results in a cycle. Kirchoff's second law is used on this cycle to obtain a circuit equation. The cycles obtained in this way are independent (i.e., none of these cycles can be obtained by taking a linear combination of the remaining cycles) as each contains an edge from B which is not contained in any other cycle. Hence, the circuit equations so obtained are also independent. In fact, it may be shown that the cycles obtained by introducing the edges of B one at a time into the resulting spanning tree form a cycle basis and so all other cycles in the graph can be constructed by taking a linear combination of the cycles in the basis (see Harary in the references for further details).
It is not difficult to imagine other applications for spanning trees. One that is of interest arises from the property that a spanning tree is a minimal subgraph G' of G such that V(G') = V(G) and G' is connected (by a minimal subgraph, we mean one with the fewest number of edges). Any connected graph with n vertices must have at least n - 1 edges and all connected graphs with n - 1 edges are trees. If the nodes of G represent cities and the edges represent possible communication links connecting 2 cities, then the minimum number of links needed to connect the n cities is n - 1. The spanning trees of G will represent all feasible choices. In any practical situation, however, the edges will have weights assigned to them. These weights might represent the cost of construction, the length of the link, etc. Given such a weighted graph one would then wish to select for construction a set of communication links that would connect all the cities and have minimum total cost or be of minimum total length. In either case the links selected will have to form a tree (assuming all weights are positive). In case this is not so, then the selection of links contains a cycle. Removal of any one of the links on this cycle will result in a link selection of less cost connecting all cities. We are, therefore, interested in finding a spanning tree of G with minimum cost. The cost of a spanning tree is the sum of the costs of the edges in that tree.
One approach to determining a minimum cost spanning tree of a graph has been given by Kruskal. In this approach a minimum cost spanning tree, T, is built edge by edge. Edges are considered for inclusion in T in nondecreasing order of their costs. An edge is included in T if it does not form a cycle with the edges already in T. Since G is connected and has n > 0 vertices, exactly n - 1 edges will be selected for inclusion in T. As an example, consider the graph of figure 6.16(a). The edges of this graph are considered for inclusion in the minimum cost spanning tree in the order (2,3), (2,4), (4,3), (2,6), (4,6), (1,2), (4,5), (1,5) and (5,6). This corresponds to the cost sequence 5, 6, 10, 11, 14, 16, 18, 19 and 33. The first two edges (2,3) and (2,4) are included in T. The next edge to be considered is (4,3). This edge, however, connects two vertices already connected in T and so it is rejected. The edge (2,6) is selected while (4,6) is rejected as the vertices 4 and 6 are already connected in T and the inclusion of (4,6) would result in a cycle. Finally, edges (1,2) and (4,5) are included. At this point, T has n - 1 edges and is a tree spanning n vertices. The spanning tree obtained (figure 6.16(b)) has cost 56. It is somewhat surprising that this straightforward approach should always result in a minimum spanning tree. We shall soon prove that this is indeed the case. First, let us look into the details of the algorithm. For clarity, the Kruskal algorithm is written out more formally in figure 6.18. Initially, E is the set of all edges in G. The only functions we wish to perform on this set are: (i) determining an edge with minimum cost (line 3), and (ii) deleting that edge (line 4). Both these functions can be performed efficiently if the edges in E are maintained as a sorted sequential list. In Chapter 7 we shall see how to sort these edges into nondecreasing order in time O(e log e), where e is the number of edges in E. Actually, it is not essential to sort all the edges so long as the next edge for line 3 can be determined easily. It will be seen that the heap of Heapsort (section 7.6) is ideal for this and permits the next edge to be determined and deleted in O(log e) time. The construction of the heap itself takes O(e) time.
In order to be able to perform steps 5 and 6 efficiently, the vertices in G should be grouped together in such a way that one may easily determine if the vertices v and w are already connected by the earlier selection of edges. In case they are, then the edge (v,w) is to be discarded. If they are not, then (v,w) is to be added to T. One possible grouping is to place all vertices in the same connected component of T into a set (all connected components of T will also be trees). Then, two vertices v,w are connected in T iff they are in the same set. For example, when the edge (4,3) is to be considered, the sets would be {1}, {2,3,4}, {5}, {6}. Vertices 4 and 3 are already in the same set and so the edge (4,3) is rejected. The next edge to be considered is (2,6). Since vertices 2 and 6 are in different sets, the edge is accepted. This edge connects the two components {2,3,4} and {6} together and so these two sets should be unioned to obtain the set representing the new component. Using the set representation of section 5.8 and the FIND and UNION algorithms of that section we can obtain an efficient implementation of lines 5 and 6. The computing time is, therefore, determined by the time for lines 3 and 4 which in the worst case is O(e log e). We leave the writing of the resulting algorithm as an exercise. Theorem 6.1 proves that the algorithm resulting from figure 6.18 does yield a minimum spanning tree of G. First, we shall obtain a result that will be useful in the proof of this theorem.
Definition: A spanning forest of a graph G = (V,E) is a collection of vertex disjoint trees Ti = (Vi, Ei), 1
Lemma 6.1: Let Ti = (Vi,Ei), 1
Proof: If the lemma is false, then there must be a spanning tree T= (V,E") for G such that E" includes E' but not e and T has a weight less than the weight of the minimum spanning tree for G including E'
Theorem 6.1: The algorithm described in figure 6.18 generates a minimum spanning tree.
Proof: The proof follows from Lemma 6.1 and the fact that the algorithm begins with a spanning forest with no edges and then examines the edges of G in nondecreasing order of weight.
Graphs may be used to represent the highway structure of a state or country with vertices representing cities and edges representing sections of highway. The edges may then be assigned weights which might be either the distance between the two cities connected by the edge or the average time to drive along that section of highway. A motorist wishing to drive from city A to city B would be interested in answers to the following questions:
(i) Is there a path from A to B?
(ii) If there is more than one path from A to B, which is the shortest path?
The problems defined by (i) and (ii) above are special cases of the path problems we shall be studying in this section. The length of a path is now defined to be the sum of the weights of the edges on that path rather than the number of edges. The starting vertex of the path will be referred to as the source and the last vertex the destination. The graphs will be digraphs to allow for one way streets. Unless otherwise stated, we shall assume that all weights are positive.
In this problem we are given a directed graph G = (V,E), a weighting function w(e) for the edges of G and a source vertex vo. The problem is to determine the shortest paths from vo to all the remaining vertices of G. It is assumed that all the weights are positive. As an example, consider the directed graph of figure 6.19(a). The numbers on the edges are the weights. If vo is the source vertex, then the shortest path from vo to v1 is vo v2 v3 v1. The length of this path is 10 + 15 + 20 = 45. Even though there are three edges on this path, it is shorter than the path vo v1 which is of length 50. There is no path from vo to v5. Figure 6.19(b) lists the shortest paths from vo to v1, v2, v3 and v4. The paths have been listed in nondecreasing order of path length. If we attempt to devise an algorithm which generates the shortest paths in this order, then we can make several observations. Let S denote the set of vertices (including vo) to which the shortest paths have already been found. For w not in S, let DIST(w) be the length of the shortest path starting from vo going through only those vertices which are in S and ending at w. We observe that:
(i) If the next shortest path is to vertex u, then the path begins at vo, ends at u and goes through only those vertices which are in S. To prove this we must show that all of the intermediate vertices on the shortest path to u must be in S. Assume there is a vertex w on this path that is not in S. Then, the vo to u path also contains a path from vo to w which is of length less than the vo to u path. By assumption the shortest paths are being generated in nondecreasing order of path length, and so the shorter path vo to w must already have been generated. Hence, there can be no intermediate vertex which is not in S.
(ii) The destination of the next path generated must be that vertex u which has the minimum distance, DIST(u), among all vertices not in S. This follows from the definition of DIST and observation (i). In case there are several vertices not in S with the same DIST, then any of these may be selected.
(iii) Having selected a vertex u as in (ii) and generated the shortest vo to u path, vertex u becomes a member of S. At this point the length of the shortest paths starting at vo, going through vertices only in S and ending at a vertex w not in S may decrease. I.e., the value of DIST(w) may change. If it does change, then it must be due to a shorter path starting at vo going to u and then to w. The intermediate vertices on the vo to u path and the u to w path must all be in S. Further, the vo to u path must be the shortest such path, otherwise DIST(w) is not defined properly. Also, the u to w path can be chosen so as to not contain any intermediate vertices. Therefore, we may conclude that if DIST(w) is to change (i.e., decrease), then it is because of a path from vo to u to w where the path from vo to u is the shortest such path and the path from u to w is the edge <u,w>. The length of this path is DIST(u) + length (<u,w>).
The algorithm SHORTEST_PATH as first given by Dijkstra, makes use of these observations to determine the cost of the shortest paths from vo to all other vertices in G. The actual generation of the paths is a minor extension of the algorithm and is left as an exercise. It is assumed that the n vertices of G are numbered 1 through n. The set S is maintained as a bit array with S(i) = 0 if vertex i is not in S and S(i) = 1 if it is. It is assumed that the graph itself is represented by its cost adjacency matrix with COST(i,j) being the weight of the edge <i,j>. COST(i,j) will be set to some large number, +
From our earlier discussion, it is easy to see that the algorithm works. The time taken by the algorithm on a graph with n vertices is O(n2). To see this note that the for loop of line 1 takes O(n) time. The while loop is executed n - 2 times. Each execution of this loop requires O(n) time at line 6 to select the next vertex and again at lines 8-10 to update DIST. So the total time for the while loop is O(n2). In case a list T of vertices currently not in S is maintained, then the number of nodes on this list would at any time be n - num. This would speed up lines 6 and 8-10, but the asymptotic time would remain O(n2). This and other variations of the algorithm are explored in the exercises.
Any shortest path algorithm must examine each edge in the graph at least once since any of the edges could be in a shortest path. Hence, the minimum possible time for such an algorithm would be O(e). Since cost adjacency matrices were used to represent the graph, it takes O(n2) time just to determine which edges are in G and so any shortest path algorithm using this representation must take O(n2). For this representation then, algorithm SHORTEST PATH is optimal to within a constant factor. Even if a change to adjacency lists is made, only the overall time for the for loop of lines 8-10 can be brought down to O(e) (since the DIST can change only for those vertices adjacent from u). The total time for line 6 remains O(n2).
Example 6.1: Consider the 8 vertex digraph of figure 6.20(a) with cost adjacency matrix as in 6.20(b). The values of DIST and the vertices selected at each iteration of the while loop of line 5 for finding all the shortest paths from Boston are shown in table 6.21. Note that the algorithm terminates when only seven of the eight vertices are in S. By the definition of DIST, the distance of the last vertex, in this case
Los Angeles is correct as the shortest path from Boston to Los Angeles can go through only the remaining six vertices.
The all pairs shortest path problem calls for finding the shortest paths between all pairs of vertices vi,vj, i
The graph G is represented by its cost adjacency matrix with COST(i.i)= 0 and COST(i,j) = +
Ak(i,j) = min {Ak-1(i,j), Ak-1(i,k) + Ak-1 (k,j)} k
and
Ao(i,j) = COST(i,j).
Example 6.2: Figure 6.22 shows a digraph together with its matrix A0. For this graph A2(1,3)
1,2,1,2,1,2, ......,1,2,3
can be made arbitrarily small. This is so because of the presence of the cycle 1 2 1 which has a length of - 1.
The algorithm ALL__COSTS computes An(i,j). The computation is done in place so the superscript on A is dropped. The reason this computation can be carried out in place is that Ak(i,k) = Ak-1 (i,k) and Ak(k,j) = Ak-1 (k,j) and so the in place computation does not alter the outcome.
This algorithm is especially easy to analyze because the looping is independent of the data in the matrix A.
The total time for procedure ALL_COSTS is O(n3). An exercise examines the extensions needed to actually obtain the (i,j) paths with these lengths. Some speed up can be obtained by noticing that the innermost for loop need be executed only when A (i,k) and A (k,j) are not equal to
Example 6.3: : Using the graph of figure 6.23(a) we obtain the cost matrix of figure 6.23(b). The initial A matrix, Ao plus its value after 3 iterations A1, A2 ,A3 is given in figure 6.24.
A problem related to the all pairs shortest path problem is that of determining for every pair of vertices i,j in G the existence of a path from i to j. Two cases are of interest, one when all path lengths (i.e., the number of edges on the path) are required to be positive and the other when path lengths are to be nonnegative. If A is the adjacency matrix of G, then the matrix A+ having the property A+ (i,j) = 1 if there is a path of length > 0 from i to j and 0 otherwise is called the transitive closure matrix of G. The matrix A* with the property A* (i,j) = 1 if there is a path of length
Figure 6.25 shows A+ and A* for a digraph. Clearly, the only difference between A* and A+ is in the terms on the diagonal. A+(i,i) = 1 iff there a cycle of length > 1 containing vertex i while A*(i,i) is always one as there is a path of length 0 from i to i. If we use algorithm ALL_COSTS with COST(i,j) = 1 if <i,j> is an edge in G and COST(i,j) = +
All but the simplest of projects can be subdivided into several subprojects called activities. The successful completion of these activities will result in the completion of the entire project. A student working towards a degree in Computer Science will have to complete several courses successfully. The project in this case is to complete the major, and the activities are the individual courses that have to be taken. Figure 6.26 lists the courses needed for a computer science major at a hypothetical university. Some of these courses may be taken independently of others while other courses have prerequisites and can be taken only if all their prerequisites have already been taken. The data structures course cannot be started until certain programming and math courses have been completed. Thus, prerequisites define precedence relations between the courses. The relationships defined may be more clearly represented using a directed graph in which the vertices represent courses and the directed edges represent prerequisites. This graph has an edge <i,j> iff course i is a prerequisite for course j.
Definition: A directed graph G in which the vertices represent tasks or activities and the edges represent precedence relations between tasks is an activity on vertex network or AOV-network.
Definition: Vertex i in an AOV network G is a predecessor of vertex j iff there is a directed path from vertex i to vertex j. i is an immediate predecessor of j iff <i,j> is an edge in G. If i is a predecessor of j, then j is a successor of i. If i is an immediate predecessor of j, then j is an immediate successor of i.
Figure 6.26(b) is the AOV-network corresponding to the courses of figure 6.26(a). C3, C4 and C10 are the immediate predecessors of C7. C2, C3 and C4 are the immediate successors of C1. C12 is a succesor of C4 but not an immediate successor. The precedence relation defined by the set of edges on the set of vertices is readily seen to be transitive. (Recall that a relation
Definition: A relation
If the precedence relation is not irreflexive, then there is an activity which is a predecessor of itself and so must be completed before it can be started. This is clearly impossible. When there are no inconsistencies of this type, the project is feasible. Given an AOV network one of our concerns would be to determine whether or not the precedence relation defined by its edges is irreflexive. This is identical to determining whether or not the network contains any directed cycles. A directed graph with no directed cycles is an acyclic graph. Our algorithm to test an AOV-network for feasibility will also generate a linear ordering, vi1, vi2, ...,vin, of the vertices (activities). This linear ordering will have the property that if i is a predecessor of j in the network then i precedes j in the linear ordering. A linear ordering with this property is called a topological order. For the network of figure 6.26(b) two of the possible topological orders are: Cl, C13, C4, C8, C14, C15, C5, C2, C3, C10, C7, C11, C12, C6, C9 and C13, C14, C15, C5, Cl, C4, C8, C2, C3, C10, C7, C6, C9, Cll, C12. If a student were taking just one course per term, then he would have to take them in topological order. If the AOV-network represented the different tasks involved in assembling an automobile, then these tasks would be carried out in topological order on an assembly line. The algorithm to sort the tasks into topological order is straightforward and proceeds by listing out a vertex in the network that has no predecessor. Then, this vertex together with all edges leading out from it are deleted from the network. These two steps are repeated until either all vertices have been listed or all remaining vertices in the network have predecessors and so none can be performed. In this case there is a cycle in the network and the project is infeasible. Figure 6.27 is a crude form of the algorithm.
Trying this out on the network of figure 6.28 we see that the first vertex to be picked in line 2 is v1, as it is the only one with no predecessors. v1 and the edges <v1,v2>, <v1,v3> and <v1,v4> are deleted. In the resulting network (figure 6.28(b)), v2, v3 and v4 have no predecessor.
Any of these can be the next vertex in the topological order. Assume that v4 is picked. Deletion of v4 and the edges (v4, v6) and(v4,v5) results in the network of figure 6.28(c). Either v2 or v3 may next be picked. Figure 6.28 shows the progress of the algorithm on the network. In order to obtain a complete algorithm that can be easily translated into a computer program, it is necessary to specify the data representation for the AOV-network. The choice of a data representation, as always, depends on the functions one wishes to perform. In this problem, the functions are: (i) decide whether a vertex has any predecessors (line 2), and (ii) delete a vertex together with all its incident edges. (i) is efficiently done if for each vertex a count of the number of its immediate predecessors is kept. (ii) is easily implemented if the network is represented by its adjacency lists. Then the deletion of all edges leading out of a vertex v can be carried out by decreasing the predecessor count of all vertices on its adjacency list. Whenever the count of a vertex drops to zero, that vertex can be placed onto a list of vertices with a zero count. Then the selection in line 3 just requires removal of a vertex from this list. Filling in these details into the algorithm of figure 6.27, we obtain the SPARKS program TOPOLOGICAL__ORDER.
The algorithm assumes that the network is represented by adjacency lists. The headnodes of these lists contain two fields: COUNT and LINK. The COUNT field contains the in-degree of that vertex and LINK is a pointer to the first node on the adjacency list. Each list node has 2 fields: VERTEX and LINK. COUNT fields can be easily set up at the time of input. When edge <i,j> is input, the count of vertex j is incremented by 1. The list of vertices with zero count is maintained as a stack. A queue could have been used but a stack is slightly simpler. The stack is linked through the COUNT field of the headnodes since this field is of no use after the COUNT has become zero. Figure 6.29(a) shows the input to the algorithm in the case of the network of figure 6.28(a).
As a result of a judicious choice of data structures the algorithm is very efficient. For a network with n vertices and e edges, the loop of lines 2-4 takes O(n) time; Lines 6-8 take O(n) time over the entire algorithm; the while loop takes time O(di) for each vertex i, where di is the out-degree of vertex i. Since this loop is encountered once for each vertex output, the total time for this part of the algorithm is
An activity network closely related to the AOV-network is the activity on edge or AOE network. The tasks to be performed on a project are represented by directed edges. Vertices in the network represent events. Events signal the completion of certain activities. Activities represented by edges leaving a vertex cannot be started until the event at that vertex has occurred. An event occurs only when all activities entering it have been completed. Figure 6.30(a) is an AOE network for a hypothetical project with 11 tasks or activities a1, ...,a11. There are 9 events v1, v2, ..., v9. The events vl and v9 may be interpreted as ''start project'' and ''finish project'' respectively. Figure 6.30(b) gives interpretations for some of the 9 events. The number associated with each activity is the time needed to perform that activity. Thus, activity a1 requires 6 days while a11 requires 4 days. Usually, these times are only estimates. Activities a1, a2 and a3 may be carried out concurrently after the start of the project. a4, a5 and a6 cannot be started until events v2, v3 and v4, respectively, occur. a7 and a8 can be carried out concurrently after the occurrence of event v5 (i.e., after a4 and a5 have been completed). In case additional ordering constraints are to be put on the activities, dummy activities whose time is zero may be introduced. Thus, if we desire that activities a7 and a8 not start until both events v5 and v6 have occurred, a dummy activity a12 represented by an edge <v6, v5> may be introduced. Activity networks of the AOE type have proved very useful in the performance evaluation of several types of projects. This evaluation includes determining such facts about the project as: what is the least amount of time in which the project may be completed (assuming there are no cycles in the network); which activities should be speeded up in order to reduce completion time; etc. Several sophisticated techniques such as PERT (performance evaluation and review technique), CPM (critical path method), RAMPS (resource allocation and multi-project scheduling) have been developed to evaluate network models of projects. CPM was originally developed in connection with maintenance and construction projects. Figure 6.31 shows a network used by the Perinia Corporation of Boston in 1961 to model the construction of a floor in a multistory building. PERT was originally designed for use in the development of the Polaris Missile system.
Since the activities in an AOE network can be carried out in parallel the minimum time to complete the project is the length of the longest path from the start vertex to the finish vertex (the length of a path is the sum of the times of activities on this path). A path of longest length is a critical path. The path v1, v2, v5, v7, v9 is a critical path in the network of figure 6.30(a). The length of this critical path is 18. A network may have more than one critical path (the path v1, v2, v5, v8, v9 is also critical). The earliest time an event vi can occur is the length of the longest path from the start vertex v1 to the vertex vi. The earliest time event v5 can occur is 7. The earlist time an event can occur determines the earliest start time for all activities represented by edges leaving that vertex. Denote this time by e(i) for activity ai. For example e(7) = e(8) = 7. For every activity ai we may also define the latest time, l(i), an activity may start without increasing the project duration (i.e., length of the longest path from start to finish). In figure 6.30(a) we have e(6) = 5 and l(6) = 8, e(8) = 7 and l(8) = 7. All activities for which e(i) = l(i) are called critical activities. The difference l(i) - e(i) is a measure of the criticality of an activity. It gives the time by which an activity may be delayed or slowed without increasing the total time needed to finish the project. If activity a6 is slowed down to take 2 extra days, this will not affect the project finish time. Clearly, all activities on a critical path are critical and speeding noncritical activities will not reduce the project duration.
The purpose of critical path analysis is to identify critical activities so that resources may be concentrated on these activities in an attempt to reduce project finish time. Speeding a critical activity will not result in a reduced project length unless that activity is on all critical paths. In figure 6.30(a) the activity a11 is critical but speeding it up so that it takes only three days instead of four does not reduce the finish time to seventeen days. This is so because there is another critical path v1,v2,v5,v7,v9 that does not contain this activity. The activities a1 and a4 are on all critical paths. Speeding a1 by two days reduces the critical path length to sixteen days. Critical path methods have proved very valuable in evaluating project performance and identifying bottlenecks. In fact, it is estimated that without such analysis the Polaris missile project would have taken seven instead of the five years it actually took.
Critical path analysis can also be carried out with AOV-networks. The length of a path would now be the sum of the activity times of the vertices on that path. For each activity or vertex, we could analogously define the quantities e(i) and l(i). Since the activity times are only estimates, it is necessary to re-evaluate the project during several stages of its completion as more accurate estimates of activity times become available. These changes in activity times could make previously non-critical activities critical and vice versa. Before ending our discussion on activity networks, let us design an algorithm to evaluate e(i) and l(i) for all activities in an AOE-network. Once these quantities are known, then the critical activities may be easily identified. Deleting all noncritical activities from the AOE network, all critical paths may be found by just generating all paths from the start to finish vertex (all such paths will include only critical activities and so must be critical, and since no noncritical activity can be on a critical path, the network with noncritical activities removed contains all critical paths present in the original network).
In obtaining the e(i) and l(i) for the activities of an AOE network, it is easier to first obtain the earliest event occurrence time, ee(j), and latest event occurrence time, le(j), for all events, j, in the network. Then if activity ai is represented by edge <k,l>, we can compute e(i) and l(i) from the formulas:
e(i) = ee(k)
and
l(i) = le(l) - duration of activity ai
The times ee(j) and le(j) are computed in two stages: a forward stage and a backward stage. During the forward stage we start with ee(1) = 0 and compute the remaining early start times, using the formula
where P(j) is the set of all vertices adjacent to vertex j. In case this computation is carried out in topological order, the early start times of all predecessors of j would have been computed prior to the computation of ee(j). The algorithm to do this is obtained easily from algorithm TOPOLOGICAL_ORDER by inserting the step
ee(k)
between lines 11 and 12. It is assumed that the array ee is initialized to zero and that DUR is another field in the adjacency list nodes which contains the activity duration. This modification results in the evaluation of equation (6.2) in parallel with the generation of a topological order. ee(j) is updated each time the ee(i) of one of its predecessors is known (i.e., when i is ready for output). The step print (j) of line 7 may be omitted. To illustrate the working of the modified TOPOLOGICAL__ORDER algorithm let us try it out on the network of figure 6.30(a). The adjacency lists for the network are shown in figure 6.32(a). The order of nodes on these lists determines the order in which vertices will be considered by the algorithm. At the outset the early start time for all vertices is 0, and the start vertex is the only one in the stack. When the adjacency list for this vertex is processed, the early start time of all vertices adjacent from v1 is updated. Since vertices 2, 3 and 4 are now in the stack, all their predecessors have been processed and equation (6.2) evaluated for these three vertices. ee(6) is the next one determined. When vertex v6 is being processed, ee(8) is updated to 11. This, however, is not the true value for ee(8) since equation (6.2) has not been evaluated over all predecessors of v8 (v5 has not yet been considered). This does not matter since v8 cannot get stacked until all its predecessors have been processed. ee(5) is next updated to 5 and finally to 7. At this point ee(5) has been determined as all the predecessors of v5 have been examined. The values of ee(7) and ee(8) are next obtained. ee(9) is ultimately determined to be 18, the length of a critical path. One may readily verify that when a vertex is put into the stack its early time has been correctly computed. The insertion of the new statement does not change the asymptotic computing time; it remains O(e + n).
In the backward stage the values of le(i) are computed using a procedure analogous to that used in the forward stage. We start with le(n) = ee(n) and use the equation
where S(j) is the set of vertices adjacent from vertex j. The initial values for le(i) may be set to ee(n). Basically, equation (6.3) says that if <j,i> is an activity and the latest start time for event i is le(i), then event j must occur no later than le(i) - duration of <j,i>. Before le(j) can be computed for some event j, the latest event time for all successor events (i.e., events adjacent from j) must be computed. These times can be obtained in a manner identical to the computation of the early times by using inverse adjacency lists and inserting the step le(k)
Using the values of ee (figure 6.32) and of le (figure 6.33) and equation 6.1) we may compute the early and late times e(i) and l(i) and the degree of criticality of each task. Figure 6.34 gives the values. The critical activities are a1,a4,a7,a8,a10 and a11. Deleting all noncritical activities from the network we get the directed graph of figure 6.35. All paths from v1 to v9 in this graph are critical paths and there are no critical paths in the orginal network that are not paths in the graph of figure 6.35 .
As a final remark on activity networks we note that the algorithm TOPOLOGICAL-ORDER detects only directed cycles in the network. There may be other flaws, such as vertices not reachable from the start vertex (figure 6.36). When a critical path analysis is carried out on such networks, there will be several vertices with ee(i) = 0. Since all activity times are assumed > 0 only the start vertex can have ee(i) = 0. Hence, critical path analysis can also be used to detect this kind of fault in project planning.
In section 6.3 we looked at the problem of finding a shortest path between two vertices. In this section we will be concerned with listing all possible simple paths between two vertices in order of nondecreasing path length. Such a listing could be of use, for example, in a situation where we are interested in obtaining the shortest path that satisfies some complex set of constraints. One possible solution to such a problem would be generate in nondecreasing order of path length all paths between the two vertices. Each path generated could be tested against the other constraints and the first path satisfying all these constraints would be the path we were looking for.
Let G = (V,E) be a digraph with n vertices. Let v1 be the source vertex and vn the destination vertex. We shall assume that every edge has a positive cost. Let p1 = r(0), r(1), ..., r(k) be a shortest path from v1 to vn. I.e., p1 starts at vr(0) = v1, goes to vr(1) and then to vr(2), ...,vn = vr(k). If P is the set of all simple v1 to vn paths in G, then it is easy to see that every path in P - {p1} differs from p1 in exactly one of the following k ways:
(1): It contains the edges (r(1), r(2)), ..., (r(k - 1), r(k))but not (r(0), r(1))
(2): It contains the edges (r(2), r(3)), ..., (r(k - 1), r(k)) but not (r(1), r(2))
:
:
(k): It does not contain the edge (r(k - 1), r(k)).
More compactly, for every path p in P - {p1} there is exactly one j, 1
(r(j), r(j + 1)), ...,(r(k - 1), r(k)) but not (r(j - 1), r(j)).
The set of paths P - {p1} may be partitioned into k disjoint sets P(1), ..., P(k) with set P(j) containing all paths in P - {P1} satisfying condition j above, 1
Let p(j) be a shortest path in P(j) and let q be the shortest path from v1 to vr(j) in the digraph obtained by deleting from G the edges (r(j - 1),r(j)),(r(j),r(j + 1)), ...,(r(k - 1),r(k)). Then one readily obtains p(j) = q, r(j), r(j + 1), ...,r(k) = n. Let p(l) have the minimum length among p(1), ...,p(k). Then, p(l) also has the least length amongst all paths in P - {p1} and hence must be a second shortest path. The set P(l) - {p(l)} may now be partitioned into disjoint subsets using a criterion identical to that used to partition P - {p1}. If p(l) has k' edges, then this partitioning results in k' disjoint subsets. We next determine the shortest paths in each of these k' subsets. Consider the set Q which is the union of these k' shortest paths and the paths p(1), ...,p(l - 1), ...,p(k). The path with minimum length in Q is a third shortest path p3. The corresponding set may be further partitioned. In this way we may successively generate the v1 to vn paths in nondecreasing order of path length.
At this point, an example would be instructive. Figure 6.38 shows the generation of the v1 to v6 paths of the graph of figure 6.37.
A very informal version of the algorithm appears as the procedure M_SHORTEST.
Since the number of v1 to vn paths in a digraph with n vertices ranges from 0 to (n - 1)!, a worst case analysis of the computing time of M_SHORTEST is not very meaningful. Instead, we shall determine the time taken to generate the first m shortest paths. Line 5 of the for loop may require determining n - 1 shortest paths in a n vertex graph. Using a modified version of algorithm SHORTEST_PATH this would take O(n3) for each iteration of the for loop. The total contribution of lkne 5 is therefore O(mn3). In the next chapter, when we study heap sort, we shall see that it is possible to maintain Q as a heap with the result that the total contribution of lines 3 and 6 is less than O(mn3). The total time to generate the m shortest paths is, therefore, O(mn3). The space needed is determined by the number of tuples in Q. Since at most n - 1 shortest paths are generated at each iteration of line 5, at most O(mn) tuples get onto Q. Each path has at most O(n) edges and the additional constraints take less space than this. Hence, the total space requirements are O(mn2)
Eulers original paper on the Koenigsberg bridge problem makes interesting reading. This paper has been reprinted in:
"Leonhard Euler and the Koenigsberg Bridges," Scientific American, vol. 189, no. 1, July 1953, pp. 66-70.
Good general references for this chapter are:
Graph Theory by F. Harary, Addison-Wesley, Reading, Massachusetts, 1972.
The theory of graphs and its applications by C. Berge, John Wiley, 1962.
Further algorithms on graphs may be found in:
The design and analysis of computer algorithms by A. Aho, J. Hopcroft and J. Ullman, Addison-Wesley, Reading, Massachusetts, 1974.
Graph theory with applications to engineering and computer science by N. Deo, Prentice-Hall, Englewood Cliffs, New Jersey, 1974.
Combinatorial Optimization by E. Lawler, Holt, Reinhart and Winston, 1976.
"Depth-first search and linear graph algorithms" by R. Tarjan, SIAM Journal on Computing, vol. 1, no. 2, 1972, pp. 146-159.
Flows in Networks by L. Ford and D. Fulkerson, Princeton University Press, 1962.
Integer Programming and Network Flows by T. C. Hu, Addison-Wesley, Reading, Massachusetts, 1970.
For more on activity networks and critical path analysis see:
Project Management with CPM and PERT by Moder and C. Phillips, Van Nostran Reinhold Co., 1970.
1. Does the multigraph below have an Eulerian walk? If so, find one.
2. For the digraph at the top of page 329 obtain:
i) the in degree and out degree of each vertex;
ii) its adjacency matrix;
iii) its adjacency list representation;
iv) its adjacency multilist representation;
v) its strongly connected components
3. Devise a suitable representation for graphs so they can be stored on punched cards. Write an algorithm which reads in such a graph and creates its adjacency matrix. Write another algorithm which creates the adjacency lists from those input cards.
4. Draw the complete undirected graphs on one, two, three, four and five vertices. Prove that the number of edges in a n vertex complete graph is n(n - 1)/2.
5. Is the directed graph below strongly connected? List all the simple paths.
6. Show how the graph above would look if represented by its adjacency matrix, adjacency lists, adjacency multilist.
7. For an undirected graph G with n vertices and e edges show that
8. (a) Let G be a connected undirected graph on n vertices. Show that G must have at least n - 1 edges and that all connected undirected graphs with n - 1 edges are trees.
(b) What is the minimum number of edges in a strongly connected digraph on n vertices? What shape do such digraphs have?
9. For an undirected graph G with n vertices prove that the following are equivalent:
(a) G is a tree;
(b) G is connected, but if any edge is removed the resulting graph is not connected;
(c) For any distinct vertices u
(d) G contains no cycles and has n - 1 edges;
(e) G is connected and has n - 1 edges.
10. A bipartite graph G = (V,E) is an undirected graph whose vertices can be partitioned into two disjoint sets V1 and V2 = V - V1 with the properties (i) no two vertices in V1 are adjacent in G and (ii) no two vertices in V2 are adjacent in G. The graph G4 of figure 6.5 is bipartite. A possible partitioning of V is: V1 = {1,4.5,7} and V2 = {2,3,6,8}. Write an algorithm to determine whether a graph G is bipartite. In case G is bipartite your algorithm should obtain a partitioning of the vertices into two disjoint sets V1 and V2 satisfying properties (i) and (ii) above. Show that if G is represented by its adjacency lists, then this algorithm can be made to work in time O(n + e) where n =
11. Show that every tree is a bipartite graph.
12. Prove that a graph G is bipartite iff it contains no cycles of odd length.
13. The following algorithm was obtained by Stephen Bernard to find an Eulerian circuit in an undirected graph in case there was such a circuit.
a) Show that if G is represented by its adjacency multilists and path by a linked list, then algorithm EULER works in time O(n + e).
b) Prove by induction on the number of edges in G that the above algorithm does obtain an Euler circuit for all graphs G having such a circuit. The initial call to Euler can be made with any vertex v.
c) At termination, what has to be done to determine whether or not G has an Euler circuit?
14. Apply depth first and breadth first search to the complete graph on four vertices. List the vertices in the order they would be visited.
15. Show how to modify algorithm DFS as it is used in COMP to produce a list of all newly visited vertices.
16. Prove that when algorithm DFS is applied to a connected graph the edges of T form a tree.
17. Prove that when algorithm BFS is applied to a connected graph the edges of T form a tree.
18. Show that A+ = A* x A where matrix multiplication of the two matrices is defined as
19. Obtain the matrices A+ and A* for the digraph of exercise 5.
20. Another way to represent a graph is by its incidence matrix, INC. There is one row for each vertex and one column for each edge. Then INC (i,j) = 1 if edge j is incident to vertex i. The incidence matrix for the graph of figure 6.13(a) is:
The edges of figure 6.13(a) have been numbered from left to right, top to bottom. Rewrite algorithm DFS so it works on a graph represented by its incidence matrix.
21. If ADJ is the adjacency matrix of a graph G = (V,E) and INC is the incidence matrix, under what conditions will ADJ = INC x INCT - I where INCT is the transpose of matrix INC. Matrix multiplication is defined as in exercise 18. I is the identity matrix.
22. Show that if T is a spanning tree for the undirected graph G, then the addition of an edge e, e
23. By considering the complete graph with n vertices, show that the number of spanning trees is at least 2n-1 - 1
24. The radius of a tree is the maximum distance from the root to a leaf. Given a connected, undirected graph write an algorithm for finding a spanning tree of minimum radius. (Hint: use breadth first search.) Prove that your algorithm is correct.
25. The diameter of a tree is the maximum distance between any two vertices. Given a connected, undirected graph write all algorithm for finding a spanning tree of minimum diameter. Prove the correctness of your algorithm.
26. Write out Kruskal's minimum spanning tree algorithm (figure 6.18) as a complete SPARKS program. You may use as subroutines the algorithms UNION and FIND of Chapter 5. Use algorithm SORT to sort the edges into nondecreasing order by weight.
27. Using the idea of algorithm SHORTEST_PATH, give an algorithm for finding a minimum spanning tree whose worst case time is O(n2).
28. Use algorithm SHORTEST_PATH to obtain in nondecreasing order the lengths of the shortest paths from vertex 1 to all remaining vertices in the digraph:
29. Rewrite algorithm SHORTEST_PATH under the following assumptions:
(i) G is represented by its adjacency lists. The head nodes are HEAD(1), ...HEAD(n) and each list node has three fields: VERTEX, COST, and LINK. COST is the length of the corresponding edge and n the number of vertices in G.
(ii) Instead of representing S, the set of vertices to which the shortest paths have already been found, the set T = V(G) - S is represented using a linked list.
What can you say about the computing time of your new algorithm relative to that of SHORTEST_PATH?
30. Modify algorithm SHORTEST_PATH so that it obtains the shortest paths in addition to the lengths of these paths. What is the computing time of your algorithm?
31. Using the directed graph below, explain why SHORTEST_PATH will not work properly. What is the shortest path between vertices v1, and v7?
32. Modify algorithm ALL_COSTS so that it obtains a shortest path for all pairs of vertices i,j. What is the computing time of your new algorithm?
33. By considering the complete graph with n vertices show that the maximum number of paths between two vertices is (n - 1)!
34. Use algorithm ALL_COSTS to obtain the lengths of the shortest paths between all pairs of vertices in the graph of exercise 31. Does ALL_COSTS give the right answers? Why?
35. Does the following set of precedence relations (<) define a partial order on the elements 1 thru 5? Why?
1 < 2; < 2 <4; 2 < 3, 3 < 4; 3 < 5: 5;< 1
36. a) For the AOE network below obtain the early, e( ), and late l( ), start times for each activity. Use the forward-backward approach.
b) What is the earliest time the project can finish?
c) Which activities are critical?
d) Is there any single activity whose speed up would result in a reduction of the project length?
37. Define a critical AOE-network to be an AOE-network in which all activities are critical. Let G be the undirected graph obtained by removing the directions and weights from the edges of the network.
a) Show that the project length can be decreased by speeding exactly one activity if there is an edge in G which lies on every path from the start vertex to the finish vertex. Such an edge is called a bridge. Deletion of a bridge from a connected graph disconnects the graph into two connected components.
b) Write an O(n + e) algorithm using adjacency lists to determine whether the connected graph G has a bridge. In case G has a bridge, your algorithm should output one such bridge.
38. Write a set of computer programs for manipulating graphs. Such a collection should allow input and input of arbitrary graphs. determining connected components and spanning trees. The capability of attaching weights to the edges should also be provided.
39. Make sure you can define the following terms.

Figure 6.2 Three sample graphs.
 v2. In addition, since E(G) is a set, a graph may not have multiple occurrences of the same edge. When this restriction is removed from a graph, the resulting data object is referred to as a multigraph. The data object of figure 6.3 is a multigraph which is not a graph.
v2. In addition, since E(G) is a set, a graph may not have multiple occurrences of the same edge. When this restriction is removed from a graph, the resulting data object is referred to as a multigraph. The data object of figure 6.3 is a multigraph which is not a graph. vj in a graph with n vertices is n(n - 1)/2. This is the maximum number of edges in any n vertex undirected graph. An n vertex undirected graph with exactly n(n - 1)/2 edges is said to be complete. G1 is the complete graph on 4 vertices while G2 and G3 are not complete graphs. In the case of a directed graph on n vertices the maximum number of edges is n(n - 1).
vj in a graph with n vertices is n(n - 1)/2. This is the maximum number of edges in any n vertex undirected graph. An n vertex undirected graph with exactly n(n - 1)/2 edges is said to be complete. G1 is the complete graph on 4 vertices while G2 and G3 are not complete graphs. In the case of a directed graph on n vertices the maximum number of edges is n(n - 1).
Figure 6.3 Example of a multigraph that is not a graph.
 V(G) and E(G')
V(G) and E(G')  E(G). Figure 6.4 shows some of the subgraphs of G1 and G3.
E(G). Figure 6.4 shows some of the subgraphs of G1 and G3.
(a) Some of the subgraphs of G1

(b) Some of the subgraphs of G3
Figure 6.4 (a) Subgraphs of G1 and (b) Subgraphs of G3

Figure 6.5 A graph with two connected components.

Figure 6.6 Strongly connected components of G3.
 .
.6.1.3 Graph Representations
 1. The adjacency matrix of G is a 2-dimensional n
1. The adjacency matrix of G is a 2-dimensional n  n array, say A, with the property that A(i,j) = 1 iff the edge (vi,vj) (<vi,vj> for a directed graph) is in E(G). A(i,j) = 0 if there is no such edge in G. The adjacency matrices for the graphs G1, G3 and G4 are shown in figure 6.7. The adjacency matrix for an undirected graph is symmetric as the edge (vi,vj) is in E(G) iff the edge (vj,vi) is also in E(G). The adjacency matrix for a directed graph need not be symmetric (as is the case for G3). The space needed to represent a graph using its adjacency matrix is n2 bits. About half this space can be saved in the case of undirected graphs by storing only the upper or lower triangle of the matrix.
n array, say A, with the property that A(i,j) = 1 iff the edge (vi,vj) (<vi,vj> for a directed graph) is in E(G). A(i,j) = 0 if there is no such edge in G. The adjacency matrices for the graphs G1, G3 and G4 are shown in figure 6.7. The adjacency matrix for an undirected graph is symmetric as the edge (vi,vj) is in E(G) iff the edge (vj,vi) is also in E(G). The adjacency matrix for a directed graph need not be symmetric (as is the case for G3). The space needed to represent a graph using its adjacency matrix is n2 bits. About half this space can be saved in the case of undirected graphs by storing only the upper or lower triangle of the matrix. A(i,j). For a directed graph the row sum is the out-degree while the column sum is the in-degree. Suppose we want to answer a nontrivial question about graphs such as: How many edges are there in G or is G connected. Using adjacency matrices all algorithms will require at least O(n2) time as n2 - n entries of the matrix (diagonal entries are zero) have to be examined. When graphs are sparse, i.e., most of the terms in the adjacency matrix are zero, one would expect that the former questions would be answerable in significantly less time, say O(e + n) where e is the number of edges in G and e << n2/2. Such a speed up can be made possible through the use of linked lists in which only the edges that are in G are represented. This leads to the next representation for graphs.
A(i,j). For a directed graph the row sum is the out-degree while the column sum is the in-degree. Suppose we want to answer a nontrivial question about graphs such as: How many edges are there in G or is G connected. Using adjacency matrices all algorithms will require at least O(n2) time as n2 - n entries of the matrix (diagonal entries are zero) have to be examined. When graphs are sparse, i.e., most of the terms in the adjacency matrix are zero, one would expect that the former questions would be answerable in significantly less time, say O(e + n) where e is the number of edges in G and e << n2/2. Such a speed up can be made possible through the use of linked lists in which only the edges that are in G are represented. This leads to the next representation for graphs.
Figure 6.7 Adjacency matrices for (i) G1, (ii) G3 and (iii) G4.

(i) Adjacency list for G1

(ii) Adjacency lists for G3

(iii) Adjacency list for G4
Figure 6.8 Adjacency Lists

Figure 6.9 Inverse adjacency lists for G3.


Figure 6.10 Orthogonal List Representation for G3.

Figure 6.11 Alternate Form Adjacency List for G1.


The lists are: vertex 1: N1
 N2
N2  N3
N3 vertex 2: N1
 N4
N4  N5
N5 vertex 3: N2
 N4
N4  N6
N6 vertex 4: N3
 N5
N5  N6
N6Figure 6.12 Adjacency Multilists for G1.
6.2 TRAVERSALS, CONNECTED COMPONENTS AND SPANNING TREES
Depth First Search
procedure DFS(v)
//Given an undirected graph G = (V,E) with n vertices and an array
VlSlTED(n) initially set to zero, this algorithm visits all vertices
reachable from v. G and VISITED are global.//
VISITED (v)
 1
1for each vertex w adjacent to v do
if VISlTED(w) = 0 then call DFS(w)
end
end DFS
Breadth First Search
procedure BFS(v)
//A breadth first search of G is carried out beginning at vertex v.
All vertices visited are marked as VISlTED(i)= 1. The graph G
and array VISITED are global and VISITED is initialized to zero.//
VISITED (v)
 1
1initialize Q to be empty //Q is a queue//
loop
for all vertices w adjacent to v do
if VISITED(w) = 0 //add w to queue//
then [call ADDQ(w,Q); VISITED(w)
 1]
1]//mark w as VISITED//
end
if Q is empty then return
call DELETEQ(v,Q)
forever
end BFS

Figure 6.13 Graph G and Its Adjacency Lists.
Connected Components
procedure COMP(G,n)
//determine the connected components of G. G has n
 1 vertices.
1 vertices.VISITED is now a local array.//
for i
 1 to n do
1 to n doVISITED(i)
 0 //initialize all vertices as unvisited//
0 //initialize all vertices as unvisited//end
for i
 1 to n do
1 to n doif VISITED(i) = 0 then [call DFS(i); //find a component//
output all newly visited vertices together
with all edges incident to them]
end
end COMP
Spanning Trees and Minimum Cost Spanning Trees
 T
T  {(v,w)} in the then clauses of DFS and BFS. The edges in T form a tree which includes all the vertices of G. Any tree consisting solely of edges in G and including all vertices in G is called a spanning tree. Figure 6.14 shows a graph and some of its spanning trees. When either DFS or BFS are used the edges of T form a spanning tree. The spanning tree resulting from a call to DFS is known as a depth first spanning tree. When BFS is used, the resulting spanning tree is called a breadth first spanning tree.
{(v,w)} in the then clauses of DFS and BFS. The edges in T form a tree which includes all the vertices of G. Any tree consisting solely of edges in G and including all vertices in G is called a spanning tree. Figure 6.14 shows a graph and some of its spanning trees. When either DFS or BFS are used the edges of T form a spanning tree. The spanning tree resulting from a call to DFS is known as a depth first spanning tree. When BFS is used, the resulting spanning tree is called a breadth first spanning tree.
Figure 6.14 A Complete Graph and Three of Its Spanning Trees.

(a) DFS (1) Spanning Tree

(b) BFS (1) Spanning Tree
Figure 6.15 DFS and BFS Spanning Trees for Graph of Figure 6.13.

Figure 6.16 Graph and A Spanning Tree of Minimum Cost.

Figure 6.17 Stages in Kruskal's Algorithm Leading to a Minimum Cost Spanning Tree.
1 T


2 while T contains less than n - 1 edges and E not empty do
3 choose an edge (v,w) from E of lowest cost;
4 delete (v,w) from E;
5 if (v,w) does not create a cycle in T
6 then add (v,w) to T
7 else discard (v,w)
8 end
9 if T contains fewer than n - 1 edges then print ('no spanning tree')Figure 6.18 Early Form of Minimum Spanning Tree Algorithm-Kruskal.
 i
i  k such that
k such that  and Ei
and Ei  E(G), 1
E(G), 1 i
i  k.
k. i
i  k, k > 1, be a spanning forest for the connected undirected graph G= (V,E). Let w be a weighting function for E(G) and let e = (u, v) be an edge of minimum weight such that if u
k, k > 1, be a spanning forest for the connected undirected graph G= (V,E). Let w be a weighting function for E(G) and let e = (u, v) be an edge of minimum weight such that if u  Vi then v
Vi then v  Vi. Let i = 1 and
Vi. Let i = 1 and  . There is a spanning tree for G which includes E'
. There is a spanning tree for G which includes E'  {e} and has minimum weight among all spanning trees for G that include E'.
{e} and has minimum weight among all spanning trees for G that include E'. {e}. Since T is a spanning tree, it has a path from u to v. Consequently, the addition of e to E" creates a unique cycle (exercise 22). Since u
{e}. Since T is a spanning tree, it has a path from u to v. Consequently, the addition of e to E" creates a unique cycle (exercise 22). Since u  V1 and v
V1 and v  V1, it follows that there is another edge e' = (u',v') on this cycle such that u'
V1, it follows that there is another edge e' = (u',v') on this cycle such that u'  V1 and v'
V1 and v'  V1 (v' may be v). By assumption, w(e)
V1 (v' may be v). By assumption, w(e)  w(e'). Deletion of the edge e' from E"
w(e'). Deletion of the edge e' from E"  {e} breaks this cycle and leaves behind a spanning tree T' that include E'
{e} breaks this cycle and leaves behind a spanning tree T' that include E'  {e}. But, since w(e)
{e}. But, since w(e)  w(e'), it follows that the weight of T' is no more than the weight of T. This contradicts the assumption on T. Hence, there is no such T and the lemma is proved.
w(e'), it follows that the weight of T' is no more than the weight of T. This contradicts the assumption on T. Hence, there is no such T and the lemma is proved. 6.3 SHORTEST PATHS AND TRANSITIVE CLOSURE
Single Source All Destinations

Figure 6.19 Graph and Shortest Paths from v0 to All Destinations.
 , in case the edge <i,j> is not in E(G). For i= j, COST(i,j) may be set to any non-negative number without affecting the outcome of the algorithm.
, in case the edge <i,j> is not in E(G). For i= j, COST(i,j) may be set to any non-negative number without affecting the outcome of the algorithm.Analysis of Algorithm SHORTEST PATH
procedure SHORTEST-PATH (v,COST,DIST,n)
//DIST(j), 1
 j
j  n is set to the length of the shortest path
n is set to the length of the shortest pathfrom vertex v to vertex j in a digraph G with n vertices. DIST(v)
is set to zero. G is represented by its cost adjacency matrix,
COST(n,n)//
declare S (1: n)
1 for i
 1 to n do //initialize set S to empty//
1 to n do //initialize set S to empty//2 S(i)
 0; DIST(i)
0; DIST(i)  COST(v,i)
COST(v,i)3 end
4 S(v)
 1; DIST(v)
1; DIST(v)  0; num
0; num  2 //put vertex v in set
2 //put vertex v in setS//
5 while num < n do //determine n - 1 paths from vertex v//
6 choose u: DIST(u) = min {DIST(w)}S(w)=0
7 S(u)
 1; num
1; num  num + 1 //put vertex u in set S//
num + 1 //put vertex u in set S//8 for all w with S(w) = 0 do //update distances//
9 DIST(w)
 min {DIST(w),DIST(u) + COST(u,w)}
min {DIST(w),DIST(u) + COST(u,w)}10 end
11 end
12 end SHORTEST-PATH

Figure 6.20(a)

Figure 6.20(b) Cost Adjacency Matrix for Figure 6.20(a). All Entries not Shown are +
 .
. Vertex LA SF D C B NY M NO
Iteration S Selected DIST (1) (2) (3) (4) (5) (6) (7) (8)
Initial -- +
 +
+ +
+ 1500 0 250 +
1500 0 250 + +
+
1 5 6 +
 +
+ +
+ 1250 0 250 1150 1650
1250 0 250 1150 16502 5,6 7 +
 +
+ +
+ 1250 0 250 1150 1650
1250 0 250 1150 16503 5,6,7 4 +
 +
+ 2450 1250 0 250 1150 1650
2450 1250 0 250 1150 16504 5,6,7,4 8 3350 +
 2450 1250 0 250 1150 1650
2450 1250 0 250 1150 16505 5,6,7,4,8 3 3350 3250 2450 1250 0 250 1150 1650
6 5,6,7,4,8,3 2 3350 3250 2450 1250 0 250 1150 1650
5,6,7,4,8,3,2
Table 6.21 Action of SHORTEST_PATH
All Pairs Shortest Paths
 j. One possible solution to this is to apply the algorithm SHORTEST__ PATH n times, once with each vertex in V(G) as the source. The total time taken would be O(n3). For the all pairs problem, we can obtain a conceptually simpler algorithm which will work even when some edges in G have negative weights so long as G has no cycles with negative length. The computing time of this algorithm will still be O(n3) though the constant factor will be smaller.
j. One possible solution to this is to apply the algorithm SHORTEST__ PATH n times, once with each vertex in V(G) as the source. The total time taken would be O(n3). For the all pairs problem, we can obtain a conceptually simpler algorithm which will work even when some edges in G have negative weights so long as G has no cycles with negative length. The computing time of this algorithm will still be O(n3) though the constant factor will be smaller. in case edge <i,j>, i
in case edge <i,j>, i  j is not in G. Define Ak(i,j) to be the cost of the shortest path from i to j going through no intermediate vertex of index greater than k. Then, An(i,j) will be the cost of the shortest i to j path in G since G contains no vertex with index greater than n. Ao(i,j) is just COST(i,j) since the only i to j paths allowed can have no intermediate vertices on them. The basic idea in the all pairs algorithm is to successively generate the matrices A0, A1, A2, ...,An. If we have already generated Ak-1, then we may generate Ak by realizing that for any pair of vertices i,j either (i) the shortest path from i to j going through no vertex with index greater than k does not go through the vertex with index k and so its cost is Ak-1(i,j); or (ii) the shortest such path does go through vertex k. Such a path consists of a path from i to k and another one from k to j. These paths must be the shortest paths from i to k and from k to j going through no vertex with index greater than k - 1, and so their costs are Ak-1(i,k) and Ak-1(k,j). Note that this is true only if G has no cycle with negative length containing vertex k. If this is not true, then the shortest i to j path going through no vertices of index greater than k may make several cycles from k to k and thus have a length substantially less than Ak-1 (i,k) + Ak-1 (k,j) (see example 6.2). Thus, we obtain the following formulas for Ak (i,j):
j is not in G. Define Ak(i,j) to be the cost of the shortest path from i to j going through no intermediate vertex of index greater than k. Then, An(i,j) will be the cost of the shortest i to j path in G since G contains no vertex with index greater than n. Ao(i,j) is just COST(i,j) since the only i to j paths allowed can have no intermediate vertices on them. The basic idea in the all pairs algorithm is to successively generate the matrices A0, A1, A2, ...,An. If we have already generated Ak-1, then we may generate Ak by realizing that for any pair of vertices i,j either (i) the shortest path from i to j going through no vertex with index greater than k does not go through the vertex with index k and so its cost is Ak-1(i,j); or (ii) the shortest such path does go through vertex k. Such a path consists of a path from i to k and another one from k to j. These paths must be the shortest paths from i to k and from k to j going through no vertex with index greater than k - 1, and so their costs are Ak-1(i,k) and Ak-1(k,j). Note that this is true only if G has no cycle with negative length containing vertex k. If this is not true, then the shortest i to j path going through no vertices of index greater than k may make several cycles from k to k and thus have a length substantially less than Ak-1 (i,k) + Ak-1 (k,j) (see example 6.2). Thus, we obtain the following formulas for Ak (i,j): 1
1 min {A1(1,3), A1(1,2) + A1(2,3)} = 2. Instead we see that A2(1,3) = -
min {A1(1,3), A1(1,2) + A1(2,3)} = 2. Instead we see that A2(1,3) = - as the length of the path
as the length of the path
Figure 6.22 Graph with Negative Cycle
procedure ALL_COSTS(COST,A,n)
//COST(n,n) is the cost adjacency matrix of a graph with n
vertices; A(i,j) is the cost of the shortest path between vertices
vi,vj. COST(i,i) = 0, 1
 i
i  n//
n//1 for i
 1 to n do
1 to n do2 for j
 1 to n do
1 to n do3 A (i,j)
 COST (i,j) //copy COST into A//
COST (i,j) //copy COST into A//4 end
5 end
6 for k
 1 to n do //for a path with highest vertex index k//
1 to n do //for a path with highest vertex index k//7 for i
 1 to n do //for all possible pairs of vertices//
1 to n do //for all possible pairs of vertices//8 for j
 1 to n do
1 to n do9 A (i,j)
 min {A (i,j),A(i,k) + A(k,j)}
min {A (i,j),A(i,k) + A(k,j)}10 end
11 end
12 end
13 end ALL_COSTS
 .
.
Figure 6.23 Directed Graph and Its Cost Matrix.
A0..1 2 3 A1 1 2 3
----------------------------
1 0 4 11 1 0 4 11
2 6 0 2 2 6 0 2
3 3
 0 3 3 7 0
0 3 3 7 0A2 1 2 3 A3 1 2 3
----------------------------
1 0 4 6 1 0 4 6
2 6 0 2 2 5 0 2
3 3 7 0 3 3 7 0
Figure 6.24 Matrices Ak Produced by ALL_COSTS for the Digraph of Figure 6.23.
Transitive Closure
 0 from i to j and 0 otherwise is the reflexive transitive closure matrix of G.
0 from i to j and 0 otherwise is the reflexive transitive closure matrix of G.



Figure 6.25 Graph G and Its Adjacency Matrix A, A+ and A*
 if <i,j> is not in G, then we can easily obtain A+ from the final matrix A by letting A+ (i,j) = 1 iff A (i,j) < +
if <i,j> is not in G, then we can easily obtain A+ from the final matrix A by letting A+ (i,j) = 1 iff A (i,j) < +  . A* can be obtained from A+ by setting all diagonal elements equal 1. The total time is O(n3). Some simplification is achieved by slightly modifying the algorithm. In this modification the computation of line 9 of ALL_COSTS becomes A(i,j)
. A* can be obtained from A+ by setting all diagonal elements equal 1. The total time is O(n3). Some simplification is achieved by slightly modifying the algorithm. In this modification the computation of line 9 of ALL_COSTS becomes A(i,j)  A (i,j) or (A(i,k) and A(k,)) and COST(i,j) is just the adjacency matrix of G. With this modification, A need only be a bit matrix and then the final matrix A will be A+.
A (i,j) or (A(i,k) and A(k,)) and COST(i,j) is just the adjacency matrix of G. With this modification, A need only be a bit matrix and then the final matrix A will be A+.6.4 ACTIVITY NETWORKS, TOPOLOGICAL SORT AND CRITICAL PATHS
Topological Sort
 is transitive iff it is the case that for all triples i,j,k, i
is transitive iff it is the case that for all triples i,j,k, i  j and j
j and j  k
k  i k.) In order for an AOV-network to represent a feasible project, the precedence relation should also be irreflexive.
i k.) In order for an AOV-network to represent a feasible project, the precedence relation should also be irreflexive.Course Number Course Name Prerequisites
Cl Introduction to Programming None
C2 umerical Analysis Cl, C14
C3 ata Structures Cl, C14
C4 ssembly Language Cl, C13
C5 utomata Theory C15
C6 rtificial Intelligence C3
C7 omputer Graphics C3, C4, C10
C8 achine Arithmetic C4
C9 nalysis of Algorithms C3
C10 Higher Level Languages C3, C4
Cll Compiler Writing C10
C12 Operating Systems Cl l
C13 Analytic Geometry and Calculus I None
C14 Analytic Geometry and Calculus II C13
C15 Linear Algebra C14
(a) Courses Needed for a Computer Science Degree at Some Hypothetical University

(b) AOV-Network Representing Courses as Vertices and Prerequisites as Edges
Figure 6.26 An Activity on Vertex Network
 is irreflexive on a set S if for no element x in S it is the case that x
is irreflexive on a set S if for no element x in S it is the case that x x. A precedence relation which is both transitive and irreflexive is a partial order.
x. A precedence relation which is both transitive and irreflexive is a partial order.input the AOV-network. Let n be the number of vertices.
1 for i
 1 to n do //output the vertices//
1 to n do //output the vertices//2 if every vertex has a predecessor
then [the network has a cycle and is infeasible. stop]
3 pick a vertex v which has no predecessors
4 output v
5 delete v and all edges leading out of v from the network
6 end
Figure 6.27 Design of a Topological Sorting Algorithm

Figure 6.28 Action of Algorithm of Figure 6.27 on an AOV Network

Figure 6.29 Input for Algorithm TOPOLOGICAL__ORDER
procedure TOPOLOGICAL__ORDER (COUNT, VERTEX, LINK, n)
//the n vertices of an AOV-network are listed in topological order.
The network is represented as a set of adjacency lists with
COUNT (i) = the in-degree of vertex i//
1 top
 0 //initialize stack//
0 //initialize stack//2 for i
 1 to n do //create a linked stack of vertices with
1 to n do //create a linked stack of vertices withno predecessors//
3 if COUNT(i) = 0 then [COUNT(i)
 top; top
top; top  i]
i]4 end
5 for i
 1 to n do //print the vertices in topological order//
1 to n do //print the vertices in topological order//6 if top = 0 then [print ('network has a cycle'); stop]7 j
 top; top
top; top  COUNT (top); print (j) //unstack a vertex//
COUNT (top); print (j) //unstack a vertex//8 ptr
 LINK (j)
LINK (j)9 while ptr
 0 do
0 do//decrease the count of successor vertices of j//
10 k
 VERTEX(ptr) //k is a successor of j//
VERTEX(ptr) //k is a successor of j//11 COUNT(k)
 COUNT(k) - 1 //decrease count//
COUNT(k) - 1 //decrease count//12 if COUNT(k) = 0 //add vertex k to stack//
13 then [COUNT(k)
 top; top
top; top  k]
k]14 ptr
 LINK(ptr)
LINK(ptr)15 end
16 end
17 end TOPOLOGICAL_ORDER
 . Hence, the asymptotic computing time of the algorithm is O(e + n). It is linear in the size of the problem!
. Hence, the asymptotic computing time of the algorithm is O(e + n). It is linear in the size of the problem!Critical Paths

Figure 6.30
(a) AOE Network. Activity Graph of a Hypothetical Project.
event interpretation
----- --------------
v1 start of project
v2 completion of activity a1
v5 completion of activities a4 and a5
v8 completion of activities a8 and a9
v9 completion of project
(b) Interpretation for Some of the Events in the Activity Graph of Figure 6.30(a).

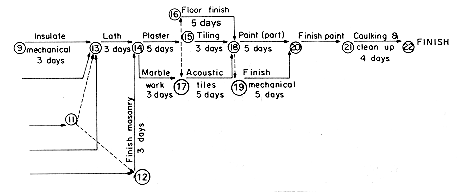
Figure 6.31 AOE network for the construction of a typical floor in a multistory building [Redrawn from Engineering News-Record (McGraw-Hill Book Company, Inc., January 26, 1961).]
(6.1)

(6.2)
 max {ee(k), ee(j) + DUR (ptr)}
max {ee(k), ee(j) + DUR (ptr)}
(a) Adjacency Lists for Figure 6.30(a)
ee (1) (2) (3) (4) (5) (6) (7) (8) (9) stack
initial 0 0 0 0 0 0 0 0 0 1
output v1 0 6 4 5 0 0 0 0 0 4
3
2
output v4 0 6 4 5 0 7 0 0 0 6
3
2
output v6 0 6 4 5 0 7 0 11 0 3
2
output v3 0 6 4 5 5 7 0 11 0 2
output v2 0 6 4 5 7 7 0 11 0 5
output v5 0 6 4 5 7 7 16 14 0 8
7
output v8 0 6 4 5 7 7 16 14 16 7
output v7 0 6 4 5 7 7 16 14 18 9
output v9
(b) Computation of ee
Figure 6.32 Action of Modified Topological Order

(6.3)
 min {le(k), le(j) - DUR(ptr)} at the same place as before in algorithm TOPOLOGICAL_ORDER. The COUNT field of a headnode will initially be the out-degree of the vertex. Figure 6.33 describes the process on the network of figure 6.30(a). In case the forward stage has already been carried out and a topological ordering of the vertices obtained, then the values of le(i) can be computed directly, using equation (6.3), by performing the computations in the reverse topological order. The topological order generated in figure 6.32(b) is v1, v4, v6, v3, v2, v5, v8, v7, v9,. We may compute the values of le(i) in the order 9,7,8,5,2,3,6,4,1 as all successors of an event precede that event in this order. In practice, one would usually compute both ee and le. The procedure would then be to compute ee first using algorithm TOPOLOGICAL_ORDER modified as discussed for the forward stage and to then compute le directly from equation (6.3) in reverse topological order.
min {le(k), le(j) - DUR(ptr)} at the same place as before in algorithm TOPOLOGICAL_ORDER. The COUNT field of a headnode will initially be the out-degree of the vertex. Figure 6.33 describes the process on the network of figure 6.30(a). In case the forward stage has already been carried out and a topological ordering of the vertices obtained, then the values of le(i) can be computed directly, using equation (6.3), by performing the computations in the reverse topological order. The topological order generated in figure 6.32(b) is v1, v4, v6, v3, v2, v5, v8, v7, v9,. We may compute the values of le(i) in the order 9,7,8,5,2,3,6,4,1 as all successors of an event precede that event in this order. In practice, one would usually compute both ee and le. The procedure would then be to compute ee first using algorithm TOPOLOGICAL_ORDER modified as discussed for the forward stage and to then compute le directly from equation (6.3) in reverse topological order.
(a) Inverted Adjacency Lists for AOE-Network of Figure 6.30(a)
le (1) (2) (3) (4) (5) (6) (7) (8) (9) stack
initial 18 18 18 18 18 18 18 18 18 9
output v9 18 18 18 18 18 18 16 14 18 8
7
output v8 18 18 18 18 7 10 16 14 18 6
7
output v6 18 18 18 18 7 10 16 14 18 4
7
output v4 3 18 18 8 7 10 16 14 18 7
output v7 3 18 18 8 7 10 16 14 18 5
output v5 3 6 6 8 7 10 16 14 18 3
2
output v3 2 6 6 8 7 10 16 14 18 2
output v2 0 6 6 8 7 10 16 14 18 1
(b) Computation of TOPOLOGICAL-ORDER Modified to Compute Latest Event Times.
le(9) = ee(9) = 18
le(7) = min {le(9) - 2} = 16le(8) = min {le(9) - 4} = 14le(5) = min {le(7) - 9, le(8)- 7} = 7le(2) = min {le(5) - 1} = 6le(3) = min {le(5) - 1} = 6le(6) = min {le(8) - 4} = 10le(4) = min {le(6) - 2} = 8le(l) = min {le(2) - 6, le(3) - 4, le(4) - 5} = 0c) Computation of le Directly from Equation (6.3) Using a Reverse Topological Order.
Figure 6.33
activity e l l - e
a1 0 0 0
a2 0 2 2
a3 0 3 3
a4 6 6 0
a5 4 6 2
a6 5 8 3
a7 7 7 0
a8 7 7 0
a9 7 10 3
a10 16 16 0
a11 14 14 0
Figure 6.34 Early, Late and Criticality Values

Figure 6.35 Graph Obtained After Deleting All Noncritical Activities.

Figure 6.36 AOE-Network with Some Non-Reachable Activities.
6.5 ENUMERATING ALL PATHS
 j
j  k such that p contains the edges
k such that p contains the edges j
j  k.
k.procedure M_SHORTEST (M)
//Given a digraph G with positive edge weights this procedure outputs
the M shortest paths from v1 to vn. Q contains tuples of the
form (p,C) where p is a shortest path in G satisfying constraints
C. These constraints either require certain edges to be included
or excluded from the path//
1 Q
 {(shortest v1 to vn path,
{(shortest v1 to vn path,  )}
)}2 for i
 1 to M do //generate M shortest paths//
1 to M do //generate M shortest paths//3 let (p,C) be the tuple in Q such that path p is of minimal length.
//p is the i'th shortest path//
4 print path p; delete path p from Q
5 determine the shortest paths in G under the constraints C and
the additional constraints imposed by the partitioning described
in the text
6 add these shortest paths together with their constraints to Q
7 end
8 end M_SHORTEST

Figure 6.37 A Graph
Shortest
Path Cost Included Edges Excluded Edges New Path
------ ---- -------------- -------------- --------
v1v3v5v6 8 none none
none (v5v6) v1v3v4v6 = 9
(v5v6) (v3v5) v1v2v5v6 = 12
(v3v5)(v5v6) (v1v3) v1v2v3v5v6 = 14
v1v3v4v6 9 none (v5v6)
none (v4v6)(v5v6)

(v4v6) (v3v4)(v5v6) v1v2v4v6 = 13
(v3v4)(v4v6) (v1v3)(v5v6) v1v2v3v4v6 = 15
v1v2v5v6 12 (v5v6) (v3v5)
(v5v6) (v2v5)(v3v5) v1v3v4v5v6 = 16
(v2v5)(v5v6) (v1v2)(v3v5)

v1v2v4v6 13 (v4v6) (v3v4)(v5v6)
(v4v6) (v2v4)(v3v4)(v5v6)

(v2v4)(v4v6) " (v1v2)(v3v4)(v5v6)

v1v2v3v5v6 14 (v3v5)(v5v6) (v1v3)
(v3v5)(v5v6) (v2v3)(v1v3)

(v2v3)(v3v5)(v5v6) (v1v2)(v5v6)
v1v2v3v4v6 15 (v3v4)(v4v6) (v1v3)(v5v6)
(v3v4)(v4v6) (v2v3)(v1v3)(v5v6)

(v2v3)(v3v5)(v5v6) (v1v2)(v1v3)(v5v6)

v1v3v4v5v6 16 (v5v6) (v2v5)(v3v5)
(v5v6) (v4v5)(v2v5)(v3v5)

(v4v5)(v5v6) (v3v4)(v2v5)(v3v5) v1v2v4v5v6 = 20
(v3v4)(v4v5)(v5v6) (v1v3)0(v2v5)(v3v5) v1v2v3v4v5v6 = 22
Figure 6.38 Action of M_SHORTEST
REFERENCES
EXERCISES



 where di = degree of vertex i.
where di = degree of vertex i. V(G) and v
V(G) and v  V(G) there is exactly one simple path from u to v;
V(G) there is exactly one simple path from u to v; V
V and e =
and e =  E
E .
.procedure EULER (v)
1 path
 {
{ }
}2 for all vertices w adjacent to v and edge (v,w) not yet used do
3 mark edge (v,w) as used
4 path
 {(v,w)}
{(v,w)}  EULER(w)
EULER(w)  path
path5 end
6 return (path)
7 end EULER
 . V is the logical or operation and ^ is the logical and operation.
. V is the logical or operation and ^ is the logical and operation.
 E(T) and e
E(T) and e  E(G), to T creates a unique cycle .
E(G), to T creates a unique cycle .


adjacent(v) connected(vp, vq)
adjacent-to(v) connected(G)
adjacent-from(v) connected component
degree(v) strongly connected
in-degree(v) tree
out-degree(v) network
path spanning tree
simple path
cycle
subgraph


