(i+j+1)/2
. (The term a is the "floor" of a; it is the largest
integer that does not exceed a.) In particular, on entry, when i=0, and j=n-1,
k=n/2. To adapt binary search to check for missing values, you simply change line 2 to Example 1(b).
Micha, a member of the computer science department at Rice University, is the author of Analysis of Algorithms: Mathematical Methods, Computational Tools (Oxford University Press, 1995). He can be contacted at hofri@cs.rice.edu.
Introduction
Binary searches are among those algorithmic staples that have uses everywhere. If you want to locate an entry in a sorted array, a binary search is the most efficient way to do so. I can't think of a college course in basic algorithms that doesn't cover binary searches.
The technique isn't perfect, however. Records must all be the same length and must be stored in a static array. If the entries are of variable length or in some kind of dynamic data structure, other less-efficient search techniques--search trees, interpolation searches, hashing, and the like--take over. But since the entry can be a key pointing to a more-complex record, binary-search techniques can be used in many situations.
This month, Micha Hofri sees how efficient he can make a basic binary-search algorithm. Why are we bothering with something so basic? Micha's analysis is interesting not so much in what it reveals about binary search, but in how the algorithm works. Good programmers do this kind of analysis with any algorithm that has significant effects on the performance of the system. (At least, they do when they have the time and budget to program right, not when the deadline is in five hours and management doesn't care what it looks like as long as it works.) Micha's trade-offs--iteration versus recursion, more simple steps versus fewer complex steps--are the type that can be made almost everywhere. Even in a world of ever-increasing processor power and clock speeds, a finely crafted algorithm is still a thing of beauty.
By the way, I am still interested in hearing your column ideas, whether you want to write a column yourself or you'd like to see a certain topic explored. You can contact me at schneier@winternet.com.
Binary search is the method of choice for searching a list for a given key value. In fact, it is the optimal comparison-based search algorithm (hashing methods can do better--with some trade-offs). To use binary search, the lists to be searched must be sorted (we assume in increasing order), of known length, and indexable in an array. This implies that the keys must be all of the same size, and that binary search can not be used to search a linked list.
These conditions mean that the ith smallest key can be directly accessed, as Ai (or A[i], using C-like notation). Binary search can be used to find a given key or to check whether or not the list contains one. The sorting implies, for example, that if the key value 6 (assuming all the keys are integers) is followed by the key value 10, then 7, 8, and 9 are not in the list.
I'll present here a basic form of binary search, which I refer to as "BS"; I'll also discuss
"BS1" and "BS2." Much of the following discussion is based on Gilles Brassard and
Paul Bratley's book Algorithmics: Theory and Practice (Prentice-Hall, 1988). Since BS is a
"divide-and-conquer" algorithm, its form is naturally recursive; see Example 1(a). Note in line 3 the comment
(i+j+1)/2. (The term a is the "floor" of a; it is the largest
integer that does not exceed a.) In particular, on entry, when i=0, and j=n-1,
k=n/2. To adapt binary search to check for missing values, you simply change line 2 to Example 1(b).
When implementing BS, a few design options are possible. All considerations are based on computing the run time. The purpose here is not just to learn about BS, but to show the power--and limitations--of this type of analysis.
The first question to resolve is the cost unit. Each basic operation in a source language (such as C) is taken as one unit, as is each comparison in BS. However, line 3 in Example 1(a), for instance, needs three operations (although some compilers can do better than that). Q denotes the cost of a function call and return; therefore, if BS terminates in line 2, its cost is Q+1; otherwise it is Q+1+3+1+another call.
To be more precise, suppose A has n entries and x is equally likely to match each of
them. If T(n) denotes the total cost of such a call, then T(1)=Q+1 and for
ngt;1, T(n)=Q+5+T(r), where r depends on the result of
the comparison in line 4 and is either k=n/2 or n-k=
n/2
(the
"ceiling" of n/2 or the smallest integer gt;/=n/2).
Although T(n) is a random variable, we deal here only with its expected value, t(n). (For a
deeper analysis, see my book Analysis of Algorithms: Mathematical Methods, Computational Tools,
Oxford University Press, 1995.) Since x is equally likely to be each of the entries, it is with
probability of n/2/2n in the lower part and n/2/n in the upper part. Figure 1 (a) presents an equation--here, a recurrence--for the mean running
time. This kind of equation is typical for divide-and-conquer algorithms. The successful approach to solving
this type of equation is:
Simplifying means replacing Q+1 by a, Q+5 by b, multiplying by n, and defining u(n)=nt(n). This leaves us with the equation in Figure 1 (b). We then choose values of n for which the troublesome floor and ceiling functions relent: powers of 2, or n=2m. The result is in Figure 1 (c).
The relation n/2=2m-1 suggests a change of notation, so we define v(m)=u(2m) as in Figure 1 (d). This is finally a standard, first-order recurrence, which can be solved by the simple iteration in Figure 1 (e).
So much for these special arguments; writing m=lg n (binary logarithm), we have
u(n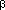)=n(
lg n+
). Clearly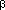, n( lg n+) cannot be
right for all values of n, since the recurrence generates integer coefficients and lg n is not
integral unless n is a power of 2. We must return to the original recurrence for u(n),
in Figure 1 (b), and use it--floors, ceilings, and all--to generate several
values, compare them with the special solution, and look for a pattern. Here, after computing about ten
values, everything falls into place; when n=2m+r, 0 lt;/=
rlt;2m, where m=lg n, then the solution in Figure 1 (f) fits all the generated values. When r=0, we get back to the
special solution. Testing by substitution into Figure 1 (b) is successful, so
t(n)=u(n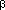)/n=+ (lg n+2r/n). Since
r/n lt; 1, this result supports the standard claim that "BS runs in logarithmic
time."
So much for the expected run time. Determining its variability requires a different kind of
computation, one that addresses the probabilistic structure directly. I show this in my book; a partial result
is that the number of iterations has only two possible values, lg n and lg n (if
n=2m, these are both m).
Having computed the expected cost of BS, let's try to reduce it. One obvious source of cost is the recursive call at each level of the procedure. This is "tail recursion," where the last instruction performed at each level is a single recursive call. The call is easy to replace using a single loop; see Example 2. The logic is identical to that of BS, except that a new call is not initiated at each level. Instead, either the left or right end of the interval is adjusted.
The logical structure of such a program parallels that of a recursive program, but the analysis is entirely
different. In BS, every instruction was done (at most) once at each level; not so in BS1. That's why the
left-most column is added in Example 2: The number of times
each line is repeated is given as a function of the searched interval size. The symbol a(n)
denotes the number of times that the main instructions (lines 4 and 5) are executed. We define
p1 as the probability that the condition in line 5 is satisfied and
q1=1-p1. We make the crucial assumption that
p1 depends in the same way on the interval size each time line 5 is reached. This is the
precise analog of the assumption we made when analyzing BS--and for the same reason. Regardless of
which subinterval still needs to be searched, the assumption that x is equally likely to be in any
position translates without change: The previous comparisons delimit the subinterval to be searched, but
provide no other information on the location of x. Hence p1 always has the same
functional form as at the first iteration, n/2/n, and
q1=n/2/n.
If ' is the cost of the lines performed once--1, 2, 3, and 8--then '=Q+2. 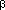' counts the cost that
recurs a(n) times--lines 3, 4, 5, 6, or 7--so 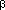'=6. The equation to determine
a(n) follows from a description of the search: Starting with an interval of size n, one
iteration leaves us with an interval of the size n/2 (in probability n/2/n) or
n/2 (with the complementary probability n/2/n); hence the equation in Figure 2 (a). Up to a factor of 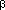, this is the same as Figure 1 (a), so the solution is familiar: n=2lg
n+r yields the result in Figure 2 (b). The amount saved by this modification is
t(n)-t1(n), and writing it in full yields the equation in Figure 2 (c).
The last relation allows us to estimate Q (without reading arcane compiled code). Table 1 represents the average time per search (in 
s) on a
standard workstation running under a UNIX-like operating system. Consider for the moment only the left
four columns; compute for each n the value lg n+2r/n and perform a linear
regression between these values and the column labeled BS-BS1. This yields the intercept -0.248 and slope
0.383. Since the intercept (in admittedly flexible units) is given in Figure 2
(c) as -1, the value of Q in these units is approximately 2.54--about two and a half basic
operations.
The cost of recursion is not trivial for a procedure with such a short body. Still, it is hardly onerous. However, this evaluation disregards two important facts:
The next modification was prompted by the observation that T(n) is essentially constant,
while BS and BS1 sometimes "locate" the desired key early in the search (BS and BS1 are
unaware of this, since equality is never tested, only inequality). The value x could be in position
n/2 (located at the first stab) but the routines would just go chugging along, only to return there
lg n steps later. Example 3 adds just such a test. While
BS1 always makes two comparisons per iteration, BS2 needs two in about half of its iterations, and three
in the other half--but presumably fewer iterations. Is this a good idea? Analysis should provide the answer:
We find in BS2 the same probability p1 used before,
Pr(xlt;A[k])=n/2/n, In addition, we have p2, defined
as the probability that x=A[k], given that x is not in the first k positions; hence
p2=1/(n-k). The dependence of the exact number of operations on the
results of the comparisons is somewhat more complex here. It is evaluated by considering the average
number of iterations BS2 will perform, again assuming that x is in the array and is equally likely to
be any element. Reading the evolution of s(n) from the code in Example 3 yields the equation in Figure
3 (a). This equation is more complex then those presented so far; for example, two initial values are
required to drive the recursion. They too can be deduced by reading BS2: s(1) is obviously 0, and
s(2) is always 1. Since k=n/2, then n-k-1=n/2-1.
Define the function b(n)ns(n), to get the equation in Figure 3 (b), where the
initial values are b(1)=0 and b(2)=2. Picking n as a power of 2 does not help as before;
instead, we pick n=2m-1,
thenn/2-1=n/2=2m-1-1. We find a
first-order recursion, similar to the equation in Figure 1 (c). This is shown
in Figure 3 (c). Using the initial value for m=1, which is
b(2-1)=1
s(1)=0, a simple unreeling reveals the solution in Figure 3 (d). Trying to guess the general solution is more difficult (I needed
more than 30 terms to see the pattern) because the increments change as n reaches 3/2
n* (where n* represents 2lg
n). Figure 4 (a) shows the
guessed solution; 
(n) is given in Figure 4 (b). Substitution confirms
this as a solution to the equation in Figure 3 (b).
Finally we compare the costs t1(n) and t2(n). First,
how many iterations, on average, does BS2 save over BS1? The difference is
a(n)-s(n), and is given in Figure 5 (a) for the
range n*
nlt;3/2n*.
As n increases from n* to 3/2n*, this difference varies from 1.5 to 0.66 (approximately). In the rest of the range, the equation in Figure 5 (b) varies correspondingly, approximately from 1.33 to 1.5. The savings are modest and are essentially independent of the size of n, but dependent on the ratio n/n*. Hence the difference between the running times can be roughly set to Figure 5 (c).
Allow the same cost C for any operation (comparison, arithmetic, or assignment) so that the two cost factors in Figure 5 (c) are nearly 6C and C (for two operations, at about half the iterations), respectively. Using only lg n*, the leading term from the solution for s(n), shows that BS1 is better when the equation in Figure 5 (d) applies.
If we take 4/3 as a representative value for 
n, we can expect the extra check in BS2
to pay off unless the array is more than about 200 entries long, with a relatively important dependence on
the ratio n/n*. Table 1 bears this
out. Since the logarithm of n* appears in this relation, the critical length is sensitive
to minor variations in the implementation. Higher precision requires consideration of the compiler and the
machine code it generates, as well as details of the machine architecture, such as availability of
increment/decrement instructions, separate data and instruction caches, and the like.
Note that in some machines, condition codes (with computed branches) allow for a three-way comparison at no added cost. If a compiler is designed to take advantage of this and can use a single comparison for lines 5 and 7 of BS2, then it will outperform BS1 on the average for any value of n. Another possibility is to code it directly in assembly language. Since binary search is used so frequently, this may be a reasonable approach.
(a) 1. BS(A[i..j],x) 2. if (i==j) return i; /* This is it! */ 3. k=(i+j+1)/2; /* Computes
(1) 1. BS1(A[n],x)
(1) 2. i=0; j=n-1;
(a(n)+1) 3. while ilt;j
(a(n)) 4. {k=(i+j+1)/2;
(a(n)) 5. if xlt;A[k]
(p1 a(n)) 6. j=k-1;
(q1 a(n)) 7. else i=k;
(1) 8. } return i;
(1) 1. BS2(A[n],x)
(1) 2. i=0; j=n-1;
(s(n)+1) 3. while ilt;j
(s(n)) 4. {k=(i+j+1)/2;
(s(n)) 5. if xlt;A[k]
(p1s(n)) 6. j=k-1;
(q1s(n)) 7. else if (xgt;A[k])
(q1q2s(n)) 8. i=k+1;
(q1p2) 9. else i=j=k;
(1) 10. } return i;
n BS BS1 BS-BS1 BS2 BS1-BS2 10 4.22 2.99 1.23 2.76 0.23 100 7.13 4.93 2.20 4.71 0.22 1000 10.18 6.88 3.30 6.99 -0.11 10000 14.96 9.87 5.09 10.45 -4.51