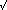N
, the
largest integer less than or equal to the square root of N. Like many tricky solutions, it's also
simple, fast, and elegant.
Peter is a video and computer game programmer who has worked on products for Amiga, PC, Sega, 3DO, and Macintosh. He's currently working for Starwave and can be contacted at peterh@starwave.com.
Complex calculation has always frustrated speed-conscious programmers, since mathematical formulas often form bottlenecks in programs that rely on them. To cope with this problem, three primary tactics have evolved: eliminate, simplify, and be tricky.
Rarely will a programmer eliminate a calculation completely. (If a program operates without it, why was it there in the first place?) Instead, integer or fixed-point may replace expensive floating-point math. At the same time, a simpler version of the formula may be sought--one which is easier to compute but gives roughly the same result.
If this proves difficult (as it often does), a tricky solution may provide the answer. This approach requires almost as much luck as programming skill, and is definitely the most difficult. Then again, the fun is in the challenge.
The square-root function certainly qualifies as a complex calculation, as anyone who has actually computed
one by hand will readily attest. In general, square roots are avoided in speed-critical code, and rank even
higher than division on the list of things to avoid. The technique I present here is an iterative approach to
finding 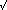N, the
largest integer less than or equal to the square root of N. Like many tricky solutions, it's also
simple, fast, and elegant.
Before attacking the actual algorithm, it might be useful to look briefly at two other iterative methods for computing the square root. Example 1(a) simply applies Newton's Method, a straightforward way to zero in on a value given an initial guess. This method is theoretically fast, having order O(log2N). Unfortunately, it uses a lot of multiplication, which may form a bottleneck in itself.
Example 1(b) uses a different approach, summing terms until they
exceed N. The number of terms summed to that point is the square root of N. While this
method eliminates the multiplication, it has a higher order of O(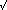
It would be nice to find a practical algorithm that also is efficient, that is, one which requires only
elementary operations but also is of low order. The Binomial Theorem suggests a possible approach. Assume
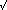N is the sum of two
numbers, u and v. Then
N=(u+v)2=u2+2uv+v2.
Choosing u and v carefully may simplify calculation of the quadratic expansion. But what
constitutes a good choice?
For any number N, it's easy to determine
Let u=2
If the sum of all three terms is less than or equal to N, the next-lower bit must be set. In that case,
the result just computed will be used for u2 and u=u+v for the next iteration. If the sum is
greater than N, the next lower bit isn't set, so u remains unchanged. In either case, move on
to the next-lower bit and repeat the process until there are no more bits to test.
Example 2(a) implements (in C) an algorithm that appears to
satisfy both design goals. It uses only elementary operations (addition and shift) and is extremely efficient,
weighing in at O(log2
Actually, many assembly languages make the first optimization moot. In fact, two of the three assembler
listings presented here use a shortcut. Only the ARM processor lacks a specialized instruction to find the
highest set bit in a number (but it's a RISC chip, after all). Listings One through Three
present implementations of the optimized algorithm for the Motorola 68020, Intel 80386, and ARM family
of processors, respectively.
For programmers developing high-performance code, complex mathematical calculation is not always
practical. Some may spurn floating-point math altogether, especially if a math coprocessor isn't guaranteed
to be present on the target platform. The algorithm I present here computes an integer square root suitable
for just such situations. Even as hardware speeds increase, programs demand more and more. Fast and
elegant little tricks like this one can still be useful.
log2N--simply find
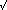the position of the highest set bit. Similarly, log2N=log2
N1/2=1/2 log2N indicates
the position of highest bit set in result, 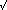N. Now the problem just entails finding which of the remaining (less
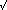
significant) bits, if any, also are set in .1/2
log2 N; that is, let u take the
value of the highest bit set in the result, 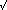N. It isn't known if the next-lower bit is also set in the result, so let v take its
value, then solve u2+2uv+v2. This calculation is easy because each term is a
simple shift. Since v is known to be a power of two, even the middle term, 2uv, reduces to a
shift operation.N). However, a few minor optimizations still can be performed: determining
1/2 log2 N can be improved; v doesn't have to be
recomputed from scratch every iteration; and noticing that
2uv+v2=v(2u+v) simplifies some computation inside the loop. Example 2(b) is the final result.Conclusion
Example 1: (a) Newton's Method; (b) summing terms.
(a)
// Newton's Method -- O( log2 N )
unsigned long sqroot( unsigned long N )
{
unsigned long n, p, low, high;
if( 2 > N )
return( N );
low = 0;
high = N;
while( high > low + 1 )
{
n = (high + low) / 2;
p = n * n;
if( N < p )
high = n;
else if( N > p )
low = n;
else
break;
}
return( N == p ? n : low );
}
(b)
// Summing terms -- O( sqrt N )
unsigned long sqroot( unsigned long N )
{
unsigned long n, u, v;
if( 2 > N )
return( N );
u = 4;
v = 5;
for( n = 1; u <= N; n++ )
{
u += v;
v += 2;
}
return( n );
}
Example 2: (a) Binomial theorem; (b) optimized binomial theorem.
(a)
// Binomial Theorem -- O( 1/2 log2 N )
unsigned long sqroot( unsigned long N )
{
unsigned long l2, u, v, u2, v2, uv2, n;
if( 2 > N )
return( N );
u = N;
l2 = 0;
while( u >>= 1 )
l2++;
l2 >>= 1;
u = 1L << l2;
u2 = u << l2;
while( l2-- )
{
v = 1L << l2;
v2 = v << l2;
uv2 = u << (l2 + 1);
n = u2 + uv2 + v2;
if( n <= N )
{
u += v;
u2 = n;
}
}
return( u );
}
(b)
// Optimized Binomial Theorem
unsigned long sqroot( unsigned long N )
{
unsigned long l2, u, v, u2, n;
if( 2 > N )
return( N );
u = N;
l2 = 0;
while( u >>= 2 )
l2++;
u = 1L << l2;
v = u;
u2 = u << l2;
while( l2-- )
{
v >>= 1;
n = (u + u + v) << l2;
n += u2;
if( n <= N )
{
u += v;
u2 = n;
}
}
return( u );
}
Listing One
MACHINE MC68020
EXPORT sqroot
;; unsigned long sqroot( unsigned long N ).
;; This routine assumes standard standard Macintosh C calling conventions,
;; so it expects argument N to be passed on the stack. Macintosh C register
;; conventions specify that d0-d1/a0-a1 are scratch.
sqroot PROC
; If N < 2, return N; otherwise, save non-scratch registers.
move.l 4(sp),d0 ; just past the return address
cmpi.l #2,d0
bcs.b done
movem.l d2-d3,-(sp)
; Compute the position of the highest bit set in the root.
; Using a loop instead of BFFFO will make this code run
; on any 680x0 processor.
movea.l d0,a0 ; preserve N for later
bfffo d0{0:0},d3
neg.l d3
addi.l #31,d3
lsr.l #1,d3
; Determine the initial values of u, u^2, and v.
moveq.l #1,d0
lsl.l d3,d0 ; u
move.l d0,d1 ; v starts equal to u
movea.l d0,a1
lsl.l d3,d1 ; u^2
exg.l d1,a1
; Process bits until there are no more.
checkBit dbf.w d3,nextBit
movem.l (sp)+,d2-d3
done rts
; Solve the equation u^2 + 2uv + v^2.
nextBit lsr.l #1,d1 ; v = next lower bit
move.l d1,d2
add.l d0,d2
add.l d0,d2 ; n = 2u + v
lsl.l d3,d2
add.l a1,d2 ; n = u^2 + v(2u + v)
; = u^2 + 2uv + v^2
; If n <= N, the bit v is set.
cmpa.l d2,a0
bcs.b checkBit
add.l d1,d0 ; u += v
movea.l d2,a1 ; u^2 = n
bra.b checkBit
END
Listing Two
NAME sqroot
PUBLIC _sqroot
;; unsigned long sqroot( unsigned long N ).
;; This routine assumes the argument N is passed on the stack, and eax-edx
;; are scratch registers.
TEXT SEGMENT PUBLIC 'CODE'
ASSUME CS:TEXT
P386
_sqroot PROC FAR
; If 2 > N, return N; otherwise, save the non-scratch registers.
mov eax,[esp+4] ; just past the return address
cmp eax,2
jb short done
push edi
push esi
; Compute position of the highest set bit in the root. It's just
; half the position of the highest bit set in N.
mov esi,eax ; preserve N for later
bsr ecx,eax
shr ecx,1
; Determine the initial values of u, u^2, and v.
mov eax,1
shl eax,cl ; u
mov ebx,eax ; v starts equal to u
mov edx,eax
shl edx,cl ; u^2
; Process bits until there are no more.
checkBit dec ecx
js short restore
; Solve the equation u^2 + 2uv + v^2.
shr ebx,1 ; v = next lower bit
mov edi,eax
add edi,eax
add edi,ebx ; n = 2u + v
shl edi,cl
add edi,edx ; n = u^2 + v(2u + v)
; = u^2 + 2uv + v^2
; If n <= N, the bit v is set.
cmp edi,esi
ja short checkBit
add eax,ebx ; u += v
mov edx,edi ; u^2 = n
jmp short checkBit
restore pop esi
pop edi
done ; Return to caller.
mov edx,eax
shr edx,16 ; necessary, but seems silly...
retf
_sqroot ENDP
TEXT ENDS
END
Listing Three
AREA object,CODE
EXPORT sqroot
;; unsigned long sqroot( unsigned long N ).
;; This routine observes the ARM Procedure Call Standard (APCS), so it expects
;; the argument N to appear in r0 (referred to as a1 by the APCS). Likewise,
;; the first four registers, r0-r3 (a1-a4 in the APCS), are treated as scratch.
sqroot ROUT
; If N < 2, return N; otherwise, save non-scratch registers.
cmp a1,#2
movcc pc,lr
stmfd sp!,{v1,v2,lr}
; Compute position of the highest bit set in root. It's just
; half the position of the highest bit set in N.
mov a2,a1 ; preserve N for later
mov a3,a1
mov v1,#0
findlog2 movs a3,a3,LSR #2
addne v1,v1,#1
bne findlog2
; Determine the initial values of u, u^2, and v.
mov a1,#1
mov a1,a1,LSL v1 ; u
mov a3,a1 ; v starts equal to u
mov a4,a1,LSL v1 ; u^2
; Process bits until there are no more.
checkBit cmp v1,#0
ldmeqfd sp!,{v1,v2,pc}
sub v1,v1,#1
; Solve the equation u^2 + 2uv + v^2.
mov a3,a3,LSR #1 ; v = next lower bit
add v2,a3,a1,LSL #1 ; n = 2u + v
add v2,a4,v2,LSL v1 ; n = u^2 + v(2u + v)
; = u^2 + 2uv + v^2
; If n <= N, the bit v is set.
cmp v2,a2
addls a1,a1,a3 ; u += v
ldmeqfd sp!,{v1,v2,pc} ; exit early if n == N
movls a4,v2 ; u^2 = n
b checkBit
END