For the case when n exceeds l, Figure 4.1 has already confirmed that as long as the three component functions work properly, then towers(n,i,a,f) will also. Note that these components correspond to smaller values of n. Mathematically inclined readers may recognize that this really amounts to a proof of correctness for towers using mathematical induction on n. One of the advantages of recursive programs is that they may be proven correct more easily in this way.
In order to understand how a recursive program actually executes, it is necessary to simulate its execution. Below are the first few steps of the simulation for a call to towers(n,i,a,f) with the values 4, 1, 2, 3 -- that is, towers(4,1,2,3). It will soon become apparent that considerable bookkeeping is involved, requiring an organized way to do it.
Since n is greater than 1, the procedure requires the sequential execution of
towers(3,1,3,2)
printf("\n %d -> %d\n",1,3);and
towers(3,2,1,3)
To do this requires suspending the execution of towers(4,1,2,3) at this point in order to simulate the first recursive call, towers(3,1,3,2). Note that after this recursive call is completed, 1?/FONT>3 is to be output. (1 ?/FONT> 3 means "Move the top disk from peg 1 to peg 3.") Then another recursive call must be simulated, towers(3,2,1,3).
Dealing with towers(3,1,3,2), since n > 1, the commands
and
must be carried out sequentially. Now the execution of towers(3,1,3,2) must be suspended in order to simulate the second recursive call, towers(2,1,2,3). Note that after this recursive call is completed, 1 ?/FONT> 2 is to be output, and then another recursive call must be simulated: towers(2,3,1,2).
Dealing with towers(2,1,2,3), since n > 1,
and
must be carried out sequentially. These two calls to towers represent the third and fourth recursive calls. They both complete without generating any new recursive calls. The three statements result in the outputting of l ?/FONT> 2, 1?/FONT> 3, and 2 ?/FONT> 3, respectively. This completes the second recursive call (towers(2,1,2,3)) so we must pick up the simulation at the proper point, which is to output l ?/FONT> 2 and then make the fifth recursive call to simulate towers(2,3,1,2).
Enough is enough! At this point you may feel like a juggler with too few hands and too many recursive calls. Figure 4.2 represents a convenient way to keep track of the complete simulation; it may be generated as the simulation proceeds. The figure traces the recursive calls made to towers as the initial call to towers(4,1,2,3) is executed to completion. Each recursive call is numbered to show whether it is the first, second, . . . , or fourteenth. The bracketed return values indicate the labeled statement of procedure towers at which the preceding recursive call is to resume when the next call is completed. For example, when towers(3,1,3,2) is completed, towers(4,1,2,3) resumes at [l]. Our simulation stopped just as the fifth recursive call was to be carried out. The figure uses shorthand for the output. For example, l ?/FONT> 2 means, "move the top disk from peg l to peg 2." The solution is the same as our earlier one.
Figure 4.2 indicates very clearly what information must be available at each point in the simulation (or execution of the program) in order to carry it out. Specifically, it is necessary to know the following information:
n The four parameter values of the call currently being carried out
n Where to resume when the call currently being carried out is completed
For example, when the third recursive call is completed, resumption must be at the printf statement of the second recursive call; when the fifth recursive call is completed, resumption must be at the end of the first recursive call; and finally, after the initial recursive call is completed, resumption must be at the proper point in the program that called towers originally.
Notice that the last three parameters are never modified by towers, but the first parameter, which corresponds to the number of disks for the current problem, is modified. For instance, the first recursive call to towers(3,1,3,2) has modified the first parameter, making it 3 rather than 4 as it was initially. It is important that this modification be kept local to towers(3,1,3,2), not reflected back to towers(4,1,2,3), the initial call.
It is not always possible to find a recursive solution to a problem, nor is it always desirable to use one when available. Sometimes a recursive solution is the only one we can find. For the Towers of Hanoi problem it is difficult to find a nonrecursive solution, but a number are known. Recursive solutions normally make it easier to see why they are correct, probably because to achieve them requires that you make the structure inherent in the problem more explicit.
To make this point clearly, the recursive algorithm and a nonrecursive algorithm are repeated here. Convince yourself that the nonrecursive algorithm solves the Towers of Hanoi problem correctly (see Exercise 8). The nonrecursive program is taken from Walsh [1982]; another nonrecursive program appears in Buneman and Levy [1980].
A Recursive Solution for the Towers of Hanoi
A Nonrecursive Algorithm for the Towers of Hanoi
l. Label the disks l, 2, . . . , n in increasing order of size.
2. Label the pegs i, a, and f, n + 1, n + 2, and n + 3, respectively.
3. Move the smallest disk onto another disk with an even label or onto an empty peg with an even label.
4. While all disks are not on the same peg
a. move the second smallest top disk onto the peg not containing the smallest disk
b. move the smallest disk onto another disk with an even label or onto an empty peg with an even label.
The Tower of Babel failed for lack of communication. The construction workers did not speak the same language. While recursion allows the solution to the Towers of Hanoi to be specified conveniently, it is execution time that causes trouble. The diagram of Figure 4.1 shows that the construction of the new tower of disks will take 24 - 1 or fifteen moves. It is not difficult to generalize the diagram to n disks to conclude that 2n - 1 moves will be needed for n disks (see Exercise 7). Even with Olympic-caliber construction workers, it would take over one thousand years to complete the tower for 50 disks.
towers(2,1,2,3)
printf("\n %d -> %d\n",1,2);towers(2,3,1,2)
towers(1,1,3,2)
printf("\n %d -> %d\n",1,3);towers(1,2,1,3)
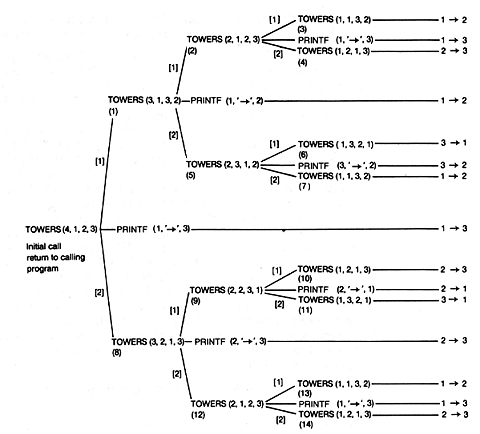
Figure 4.2 Bookkeeping for the Simulation of a Recursive Program
To obtain towers(n,i,a,f):
If n = 1, then
move the top disk from i to f
else
apply towers (n - 1,i,f,a)
move the top disk from i to f
apply towers(n - 1,a,i,f).