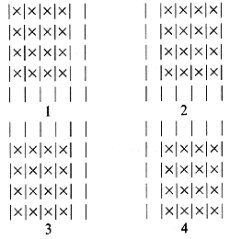
For this particular example the solution is easy to see by inspection. However, how do you state an algorithm that produces the result in all cases? This can be done handily using recursion. Suppose you know the number of ways, f(n - 1), in which the 4 ?/FONT> 4 board can be placed on an (n - 1) ?/FONT> (n - 1) board. An additional (n - 3) + (n - 4) placements result from an n ?/FONT> n board, because of the n cells
added at the top and left sides of the (n - 1) ?/FONT> (n - 1) board, as shown in Figure 4.5. There are a total of f(n) = f(n - 1) + (n - 3) + (n - 4) placements for the n ?/FONT> n board, when n ?/FONT> 5. If n = 4, f(4) = 1. So the following is true.
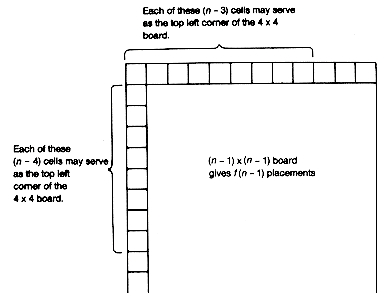
Figure 4.5 An n x n Checkerboard
f(n) is
1 if n = 4
f(n - 1) + (n - 3) + (n - 4) if n ?/FONT> 5