Chess is played on a square board with eight rows and eight columns, just like a checkerboard. We can think of the board as a two-dimensional array, board (Figure 7.16).
A queen located in the jth row and kth column may move to a new position in one of the following ways:
n To the right, or left, along its row
n Up, or down, in its column
n Up, or down, along its d1 diagonal
n Up, or down, along its d2 diagonal
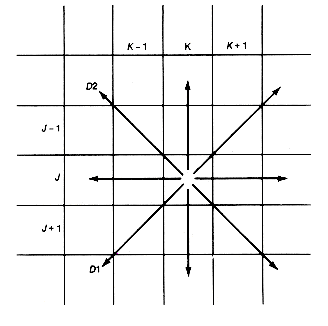
Figure 7.16 A Partial Chessboard Represented as a Two-Dimensional Array, BOARD
The n-queens problem is to find all ways to place n queens on an n ?/FONT> n checkerboard so that no queen may take another. As an example, the eight-queens problem is to find all ways to place eight queens on the chessboard so that no queen may take any other梩hat is, move into a position on its next move that is occupied by any other queen.
The question is how to solve the n-queens problem. At first glance this problem has little relation to trees, but let us see. It is not even clear that a solution exists for all n.
Since a queen can be moved along one of its rows, columns, or diagonals, a solution clearly is achieved by specifying how to place the n queens so that exactly one queen appears in each row and column, and no more than one queen appears on any diagonal of the board. One could attempt to find a solution by searching through all possible placements of the n queens satisfying these restrictions. There are, however, n! such placements. Even for a moderate n, this is obviously not a practical solution. Instead we must construct a solution. The idea behind the construction is to determine if the placements obtained for the first i queens can lead to a solution. If they cannot, abandon that construction and try another, since placing the remaining n - i queens will not be fruitful. This may avoid the need to consider all possible constructions.
To construct a solution involves testing a partial construction to determine whether or not it can lead to a solution or must be abandoned as a dead end. This testing is the next question.
Consider a general tree, with each of its nodes representing a sequence of decisions on the placement of queens. Take the root to represent the initial situation, in which no decisions have yet been made. The root will have n successors. Each successor corresponds to a choice of row for the placement of the first queen. Each of these successor nodes, in turn, has n successors, corresponding to a choice of row for the placement of the second queen, and so on. The tree for the four-queens problem is shown in Figure 7.17.
Since exactly one queen must appear in each column in any solution, assume the ith queen is placed in column i. Hence, each path, from the root to a node at depth i in the tree, specifies a partial construction in which the first i queens have been placed on the board. The path indicated in the four-queens tree specifies a partial construction in which the first, second, and third queens have been placed in rows 2, 4, and 1 (and columns 1, 2, and 3), respectively. The tree helps us visualize all possible solutions and provides a framework in which to view what we are doing.
Suppose a path has been found to a node at depth k. The path is feasible if none of the k queens whose positions are specified by the path can take any other. If the node at depth k is a terminal node, and the path is feasible, then a solution has been found and may be printed. If the node at depth k is not terminal, and the path is feasible, we want to extend the path to a node at depth k + 1. Let p point to such a node. Then node.p must be a successor of the node on the path at depth k.
P is feasible if the position that node. p specifies for the (k + 1)th queen does not allow it to take any of the other k queens. If p is feasible, the path can be extended downward in the tree to include node.p, so there is now a feasible path of depth k + 1. If p is not feasible, then another successor of the node at depth k must be tried until a feasible one is found to extend the path, or until all have been tried and none is feasible. In the latter case, the choice of node at depth k cannot be extended to a solution, and the computer backs up in the tree to a node representing a shorter path that has not yet been explored. This procedure to extend the new path is repeated until a solution is found or until all possibilities have been tried.
The procedure described amounts to a modified general tree traversal called backtracking. A different approach would be to create an algorithm for the problem by applying a general tree preorder traversal that uses a process routine. The process routine would check each node to be processed to see whether the node is terminal and represents a feasible path. If so, it prints the solution. This approach amounts to an exhaustive search of all n! possibilities, since the preorder traversal backs up only when the preorder traversal of a subtree has been completed?/FONT>that is, after a terminal node has been processed. The backtracking traversal need not access and process all nodes. It backs up when the traversal of a subtree has been completed or when it becomes known that no path involving the root of a subtree can be extended to a solution. The backtracking procedure generates only feasible paths?/FONT>not all paths. In effect, it prunes the tree by ignoring all nodes that cannot lead to a solution.
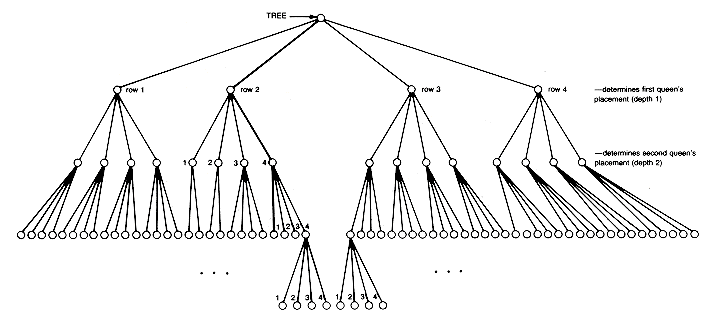
Figure 7.17 Tree for the Four-queens Problem