What else can be tried to improve the insertion sort? Aha, lists! Recall that lists are convenient for insertions, so simply represent the records in a list rather than an array. Then, once you know where to insert a record, merely change two pointers. Thus the 1 + 2 + ?/FONT> ?/FONT> ?/FONT> + (n - 1) or [n(n - 1)]1/2 insertion time is reduced to time O(n). The list, coupled with the binary search reduction in comparison time to n 1g n, seems to give a new implementation of the insertion sort with worst-case time n 1g n. The fly in this ointment is that the ability to do a binary search has disappeared. It is no longer possible to locate the middle record by selection, which is what makes the binary search with sorted arrays so fast. Just the first record's location is known; the middle record can be found only by traversing the list and counting records until the middle one is reached.
Wait! We are not yet defeated in our quest for a faster insertion sort. Use a pointer array, assuming enough storage is available, to tell where all the records are on the list. This allows selection of the list records as in Chapter 2. The situation is then as shown in Figure 8.6.
Numberlist is the head of the list of records in the illustration. Suppose the first six records have been properly processed as in the insertion sort, and the seventh is to be processed next. A binary search can now be done, since the middle record, among 1 to 6, will be indexed by the middle entry of elements 1 to 6 of the pointer array. Thus it is possible, in 1g 6 time, to determine where the seventh record is to be inserted. The insertion will require the changing of two pointers. But here's the rub! To maintain the pointer array, it must have its seventh element inserted in the corresponding position of the pointer array. We have merely succeeded in transferring the insertion problem to the pointer array; we have not eliminated it!
Although these attempts to find a faster sorting algorithm have so far not been successful, they provide insight into the binary search and sorting problems. First, notice that except for the binary search, all the searching and sorting algorithms so far considered may be applied to records stored in lists as well as in arrays. Observe that to achieve both a search in binary search time (lg n) and fast insertions and deletions, a linked type structure is needed, as well as some way to eliminate from consideration a significant fraction of the records. A second observation is that the original insertion sort would be faster if the length of the array in which each insertion is made were shorter. We must somehow break up the array of records to be sorted, so that the individual insertions do not involve all of the previous records. These observations lead to the ideas behind heapsort and quicksort, two faster sorting algorithms.
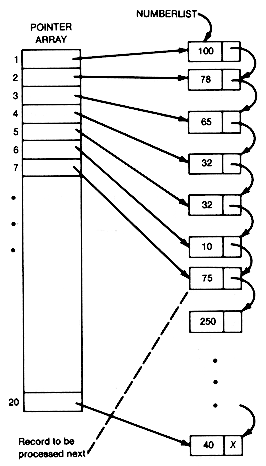
Figure 8.6 Selection of Records by Means of a Pointer Array