Consider the initial complete binary tree in Figure 8.12(a). Start at node 5 ( = ?/FONT>11/2?/FONT>) (83 is stored there) and compare its successors 94 and 7, determining that 94 is the larger. Compare 94 with 83; since 94 exceeds 83, interchange 94 and 83 to obtain Figure 8.12(b).
The subtree with node 5 (94) as root is now a heap. Move to node 4, and the similar comparisons reveal that it is already a heap. Move to node 3, compare its successors 29 and 30, and then compare the larger to 16. Since 30 exceeds 16, interchange 30 and 16 to obtain Figure 8.12(c).
The subtree of node 3 is a heap, so move to node 2. Compare its successors 57 and 94, and then compare the larger to 14. Interchange 94 and 14 to obtain Figure 8.12(d).
At this point, notice that all nodes processed so far must be the roots of subtrees that remain heaps, except perhaps for the root of the subtree, where 14 now appears after the interchange. This subtree need not be a heap and, in fact, is not in this case. You can make it a heap by applying the same process to the node where 14 is currently stored, node 5. Compare its two successors and then compare the larger of those with 14. Then interchange 14 and 83 to obtain Figure 8.12(e).
The subtree with root node 2 is now a heap, and the processing of node 2 is complete. Notice that all nodes processed so far are roots of subtrees that are heaps. The last node to be processed is now node 1. Compare its successors, 94 and 30. Since the larger, 94, exceeds 18, interchange to obtain Figure 8.12(f).
The 18 from the node being processed, node 1, has now moved down to node 2. Hence its subtree may no longer be a heap. Apply the process to node 2. The 18 can move down again and will continue to move down until it either becomes situated at a terminal node or becomes the root of a subtree that remains a heap. In this case, it should be compared with 83, the larger of its two successors, and interchanged to get Figure 8.12(g).
At this point, you can see that 18 is the root of a heap by comparing it to the larger of its two successors. Processing of node 1 has been completed, and the heap has been created. The heap obtained from the original example with this algorithm is Figure 8.12(h). Notice that this heap differs from that in Figure 8.8(a). As mentioned earlier, more than one heap can be constructed to store the same data.
Without analyzing this heap creation algorithm in detail, the result can be stated. This procedure is actually only O(n). This heap creation algorithm is faster than that of the last section because few nodes must move down long paths. In the other algorithm, many nodes may move up long paths. A use for this linear time heap creation algorithm will be demonstrated in another context in Section 9.2, Priority Queues.

Figure 8.12 A Fast Heap Creation
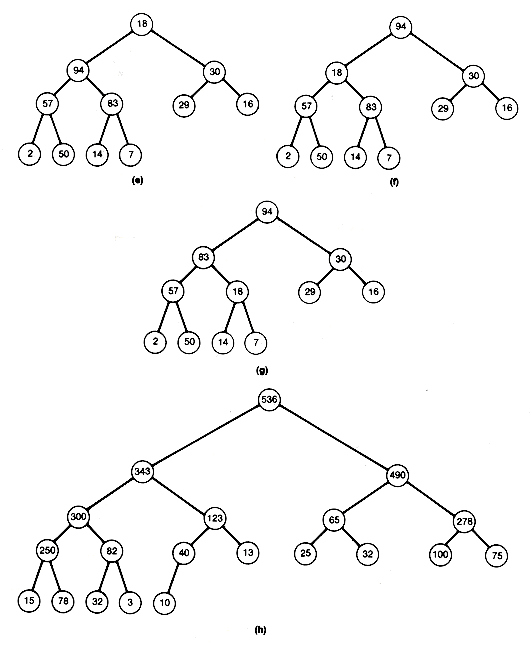
Figure 8.12