The storage required by the heapsort algorithm in the implementation is O(n). A reasonable measure for the time required is given by the number of interchanges and comparisons necessary to produce a sort. Assume that a procedure treesort has been written that is one of the detailed implementations discussed previously for heapsort. It has parameters n, a, sa, int1, int2, comp1, and comp2. These represent, respectively, the number of records, the input array of records to be sorted, the output array of sorted records, the number of interchanges required in phases I and II, and the number of comparisons required in phases I and II.
The simulation program to be written must explore the time requirements, as measured by int1, int2, comp1, and comp2, for various values of n, such as 20, 40, 60, 80, and 100. This will suggest how the execution time depends on n. Alternatively, the actual execution times could be measured. Intuitively, the algorithm will have fastest execution time when the input is nearly sorted, the slowest time when the input is nearly reverse sorted. For random initial orderings, the time can be expected to fall between these two extremes. This may not be the case but seems likely a priori. Consequently, we want to generate a number of samples from each of these three distinct classes of input, execute the treesort routine for each sample, and collect statistics on the numbers of interchanges and comparisons based on the samples taken.
We will choose twenty-five samples of each type of input, for a total number of executions of treesort of (twenty-five samples for each input class and value of n) x 3 input classes x 5 values of n, or 375 runs. One way to see if twenty-five samples is enough to achieve good statistics is to run an additional twenty-five. If the results do not vary significantly, then the twenty-five samples, or perhaps even fewer, are sufficient. If necessary, we can use a larger number of samples. Remember, the twenty-five samples are taken from a possible number of n! samples. It may seem the height of foolishness to base estimates on such a ridiculously small fraction of the possibilities. Thank goodness for statistics (when properly applied).
For each of the twenty-five samples for a given input class, the task is to find the following statistics for int1, int2, comp1, and comp2: their minimum, average, and maximum over all twenty-five sample values. Other statistics, such as the range and standard deviation, could be calculated if needed. We will have the simulation program print this information for each value of n, as indicated for n = 40 in the chart on the previous page. The *'s represent actual numeric values that will be output. A total of thirty-six values will be printed for each n; 5 ?/FONT> 36 =180 statistics.
The program will keep statistics tables, one table for each input class for the current value of n. An algorithm for the simulation program is as follows:
1. Set n to 20.
2. While n ?/FONT> 100
a.Set ns to 1.
b. Initialize statistics tables.
c. While ns ?/FONT> 25,
i. Generate a sample from each input class, call treesort to work on each input, and then update the appropriate statistics tables.
Set ns to ns+1.
d. Output the statistics tables for the current value of n and for each input class.
e. Set n to n+20.
Task (i) may be carried out as follows:
a. Generate a "random" sample for a of size n and call treesort(n, a, sa, int1, int2, comp1, comp2).
b. Update the statistics table for "random" input.
c. Generate a "nearly sorted" input for a of size n by making 20 percent of n random interchanges on sa. Copy sa into a.
d. Generate a "nearly reverse sorted" input for a of size n by copying sa in reverse order in ra. Call treesort(n, a, sa, int1, int2, comp1, comp2).
e. Update the statistics tables for "nearly sorted" input.
f. Call treesort(n, ra, sa, int1, int2, comp1, comp2).
g. Update the statistics table for "nearly reverse sorted" input.
h. Set ns to ns+1.
At this point we can explain in more detail what is meant by the three classes of input. Assume that all input arrays, a, will contain integers between 1 and 1,000. Random inputs for a of size n are generated by placing the n integers into a in such a way that all orderings of the n numbers are equally likely. Consider the two arrays shown in Figure 8.19.
Array (b) has been obtained from array (a), which is sorted, by making two interchanges. These were interchanging a1[2] with al[6], and interchanging a1[4] with a1[9] . These two interchanges represent 20 percent of n interchanges, since n is 10. A nearly sorted input for a of size n is obtained by making 20 percent of n such interchanges in an initially sorted array. The interchanges are to be selected at random. This means that each interchange is obtained by picking a value for i at random, so that each of the locations 1 to n of sa is equally likely to be selected. An integer j may be similarly obtained. Then sa[i] and sa[j] are interchanged. The only details still left to implement in the simulation algorithm are how to generate the required random integers to be placed in a and used for interchange locations, how to update the statistics tables, and how to finalize the tables before printing them.
Assume that a function rng is available that returns a real number as its value. This real number will be greater than 0.0 and less than 1.0. Whenever a sequence of these numbers is generated by consecutive calls to rng, the numbers appear, from a statistical point of view, to have been selected independently. Also assume that the returned value will lie in a segment of length l between 0 and 1, with probability l. For example, if l is of length 0.25, then the returned value will lie in that interval (say, between 0.33 and 0.58) 25 percent of the time. The random number generator ranf of FORTRAN is an example of such a function.
To generate an integer between 1 and 1,000, take the value rng returns, multiply it by 1,000, take the integer part of the result, and add 1 to it. For example, if the value returned is 0.2134, multiplying by 1,000 gives 213.4. Its integer part is 213; adding 1 yields 214. In fact, if any number strictly between 0.213 and 0.214 had been returned, 214 would have been generated. Hence 214 would be generated with probability 1/1,000, the length of the interval from 0.213 to 0.214. The same is true for each integer between 1 and 1,000. Carrying out this procedure n times will fill the array a to generate a "random" input (See Exercise 23 for a more exact approach). An alternative method in C to generate an integer at random between integers low and high uses the library function rand. Evaluating rand()%(high-low+1) + low yields the desired integer between low and high. n = 40
-------------
Input Class Min Ave Max
------------------------------------
"Nearly sorted" int1 * * *
int2 * * *
comp1 * * *
comp2 * * *
"Random" int1 * * *
int2 * * *
comp1 * * *
comp2 * * *
"Nearly reverse int1 * * *
sorted" int2 * * *
comp1 * * *
comp2 * * *
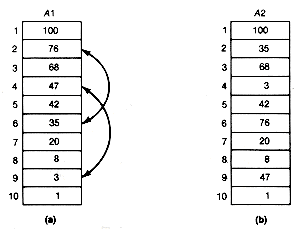
Figure 8.19 Array (b) Obtained from Sorted Array (a) by Two Interchanges