1. It is a heap.
2. Its left and right subtrees are leftist trees.
3. The path that is obtained by starting from the root and branching to the right until a node with no right successor is reached is the shortest path from the root to any node with at most one successor.
For example, the tree (a) of Figure 9.1 violates condition 3, while the trees (b) and (c) are leftist trees.
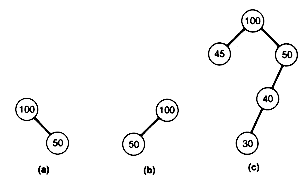
Figure 9.1 One Nonleftist and Two Leftist Trees
As an exercise, you should prove by induction on the number of nodes, n, in a leftist tree, that the shortest path in the tree, from the root to a node with at most one successor, contains at most ?/FONT>lg (n + 1)?/FONT> nodes. Such a shortest path can always be obtained by traversing the right chain from the root.
Leftist trees are implemented using a linked representation. (See Figure 9.2) Each node's record has an additional field, the distance field, containing the number of nodes along the right chain.
A leftist tree implementation of a priority queue has a number of pluses. Both additions and deletions can be done in constant time when the priority queue is acting as a stack. The time for these operations is O(lg n) for the general case. Also, two priority queues can be merged into one in O(lg n) time, where n is the total number of entries in the two priority queues to be merged. This is significantly faster merging than can be done with any of the previous methods, except for unordered lists. Crane [1972] introduced leftist trees as a data structure that can be used to implement priority queues. (See Knuth [1973b] for more details.)
The algorithm for merging two priority queues represented as leftist trees in O(lg n) time is as follows:
1. Make node.p the root of the merged tree, and merge q with p's right subtree.
2. Update the distance field of node.p.
3. If the distance of the root of the left subtree is not at least as great as the distance of the root of its right subtree, then interchange the two subtrees.
P is assumed to point to that root of the two leftist trees to be merged which contains the maximum key value, and q points to the other root. The result of merging the two trees p and q is shown as the tree r. The distance field values appear in parentheses. Notice in Figure 9.2 that, in effect, the two right chains of p and q are merged, with the other subtrees coming along for the ride. It is because only these two shortest paths participate in the algorithm that the time is O(lg n).
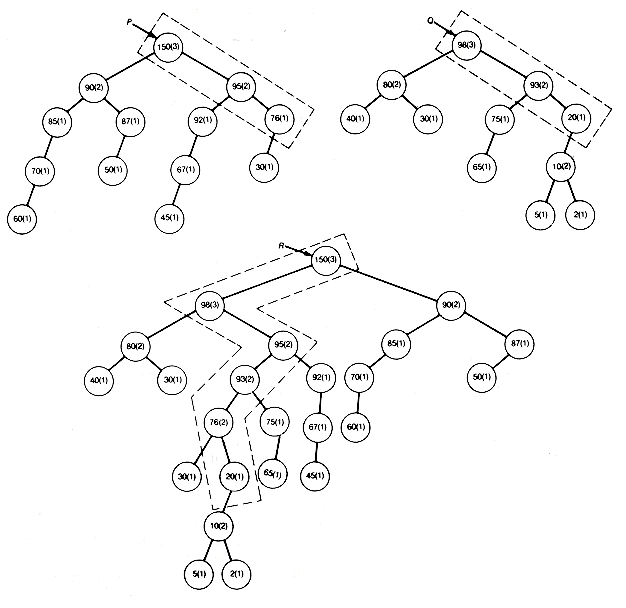
Figure 9.2 The Merging of Leftist Trees Implemented in Linked Representation