Let h(k) denote the hash function value for search key k. The sequence of indexes determined by
[h(k) + i ?/FONT> p(k)]mod m* for i = 0, 1, 2, . . . , m - 1
is a probe sequence if the indexes are all distinct. This implies that, as i goes from 0 to m - 1, the generated indexes form a permutation of the indexes 0, 1, 2, . . . , m - 1. Consequently, in attempting a new key insertion, all locations of the hash table will be accessed in some order before deciding that the key cannot be inserted. It also ensures that, in attempting to search for a key, all locations of the table will be accessed in some order before concluding that the search key is not in the table, or until a null key is encountered.
* The formula states that the ith index in the probe sequence is found by calculating [i + p(k)]mod m. However, if the previous index, the (i - 1)th, is known, then simply adding p(k) to it and taking the result mod m will also yield the ith index.
Linear probing is the special case obtained by taking p(k) = 1 for all keys k. In general, a key is inserted by accessing the table locations given by its probe sequence, determined by [h(k) + i ?/FONT> p(k)]mod m as i goes from 0 to m - 1, until a null key is encountered. The key is then inserted in place of that null key. A search is done the same way. The algorithm for a hash table search using a probe sequence is as follows:
1. Set i to h(k)
2. While ki is not the search key k and ki is not the null key
set i to [i + p(k)]mod m.
3. If ki = k, then
set found to true
else
set found to false.
Notice that p(k) represents a displacement from the current probe address.
With linear probing, large clusters of keys stored in adjacent locations of the hash table tend to get larger as insertions are made. This is because large clusters have a greater probability of the new keys' hash address falling within the cluster, assuming a "random" hash function and "random" keys. A cluster gets larger when a new key is inserted at either end of the cluster, or when two separated clusters become connected because of the new key insertion. Both of these events occurred in the scaled-down social security number example. This phenomenon is called primary clustering. As the table usage ratio increases, primary clustering leads to greater search and insertion times. This is clearly undesirable. It happens because the large clusters must be traversed, with the average time being proportional to half the cluster length when keys are searched with equal frequency. Thus the insertion, or search for a key, begins to look like a linear search through a cluster.
To avoid primary clustering, try taking the next probe to be in a position removed from the current one instead of being adjacent to it. This is open addressing with displaced linear probing. Taking p(k) = a for some integer a that is not a factor of m will give such a probe sequence. To see this, take m = 13 and a = 5. The probe sequence is then generated by [h(k) + i ?/FONT> 5] mod 13 for i = 0, 1, 2, . . . , 12. If h(k) = 7, this gives the probe sequence
7, 12, 4, 9, 1, 6, 11, 8, 0, 5, 10, 2
Note that any key k whose hash address is 7 will have exactly the same probe sequence. Even worse, suppose a key's hash address is 11, and 11 is occupied upon its insertion. The next probe for this key will be in location [11 + 1 ?/FONT> 5] mod 13, which is location 3. A collision at 3 will result in a further probe at [3 + 1 ?/FONT> 5] mod 13 or 8, then 0, 5, etc. Thus the key that originally hashed to address 11 picks up at the intersection of 11 with the probe sequence for any key hashing to 7, and follows that same probe sequence from 11 onward. Similarly, any key that collides, upon insertion, with a key already occupying its hash address, will continue along this exact probe sequence from its point of entry.
In effect, there is exactly one probe sequence for all keys; they just enter, or merge into it, at different positions specified by their hash addresses. This means that, as a "cluster" builds up along this probe sequence (say, at 11, 3, 8, 0, and 5, as they become occupied), it has the same tendency to grow as a cluster of physically adjacent occupied addresses did with linear probing. This is just primary clustering, although the clusters do not appear in adjacent locations.
We need effective techniques for dealing with this problem. Figure 9.4 gives the hash tables that result from their application to our example. The hash tables produced by linear probing, and the displaced linear probing just discussed, appear in tables (a) and (b) of the figure, corresponding to a = 1 and a = 4, respectively. In addition, the number of probes required for the insertion of each key is indicated for each table. You should create these tables yourself to confirm their correctness and to aid in understanding the discussion.
The average number of probes for a successful search of this table is 1/18 ?/FONT> (11 ?/FONT> 1 + 5 ?/FONT> 2 + 1 ?/FONT> 3 + 1 ?/FONT> 12) = 36/18 or 2.00, which is an improvement over linear probing for this example. However, for the reasons stated previously, the theoretical average number of probes in a successful search will be the same as for linear probing.
How can we eliminate or break up large clusters to improve these results? It can be done using open addressing with secondary clustering. Consider the following analogy. Suppose there are m stores, each selling a certain specialty item, and each with exactly one such item in stock. Assume n people decide to buy that item the same day, and they, in turn, each select one of the m stores at random. If a customer finds the item in stock at the shop of his or her choice, he or she buys it. However, if someone has already bought the item, it will be out of stock, and the person may ask the store manager for directions to another store. Let the stores be numbered from 0 to m - 1. Whenever this occurs, suppose the manager of the ith shop sends the customer to the (i + 1)th shop. Of course, the manager of the (m - 1)th store refers people to the 0th store. The result of all this feverish activity is that all customers arriving at a particular out-of-stock store are sent to the same next store. Again, at that store, they are all sent to the same next store whenever the item has been sold. It seems clear that this results in primary clusters of customers being formed. The physical locations of the stores is irrelevant to this process.
Suppose each store manager, instead of giving identical directions to each would-be purchaser, sends customers to another store depending on which store they tried originally and on the number of stores they have already been to. The effect will be to disperse the unhappy customers. Rather than all these people being sent on to the same sequence of shops, only those with the same initial shop and the same number of previous attempts at buying are given identical directions. Clusters should still appear, but they should tend to be smaller than the primary clusters. This is, in fact, what happens, and the clusters that appear after such dispersion are called secondary clusters.
Translating this remedy to the problem involves choosing p(k) so that it becomes a function of h(k), the initial hash address of key k. This implies that only keys hashing to the same address will follow identical probe sequences. Unlike linear or displaced linear probing, keys whose probe sequences intersect do not merge into the same probe sequence at intersection. They go their separate ways. Again, to ensure that p[h(k)] generates a probe sequence, it is necessary to choose it carefully. As long as p[h(k)] is not a factor of m, for each key k, a probe sequence will result. If m is a prime number, this will always be the case when p[h(k)] is between 0 and m - 1.
As an example, take
Using our h(k) = k mod m and m = 13, any key with hash address 7 (say, key 137) has the probe sequence
7, 5, 3, 1, 12, 10, 8, 6, 4, 2, 0, 11, 9
Any key hashing to 11 now (say, key 258) has the probe sequence
11, 0, 2, 4, 6, 8, 10, 12, 1, 3, 5, 7, 9
Notice that a collision at 11, for such a key, does not result in the probe sequence for keys with hash address 7 being followed from its intersection with 11. It follows the sequence 11, 0, 2, . . . instead of 11, 9, 7, 5, . . . .
The hash table for this secondary clustering remedy is hash table (c) of Figure 9.4. The average number of probes for a successful search in this table is 1/18 ?/FONT> [(11 ?/FONT> 1) + (3 ?/FONT> 2) + (3 ?/FONT> 3) + (1 ?/FONT> 5)] = 31/18 or 1.72. This gives an improvement over hash tables (a) and (b), as expected. It occurs because the secondary clusters tend to be shorter than the primary clusters. Notice that the "physically adjacent" clusters in the table are deceiving; they are not relevant. It is the clustering along the probe sequences that is important. In linear and displaced linear probing there is, in effect, only one probe sequence. With the secondary clustering techniques, there is a distinct probe sequence for each distinct hash address.
Open addressing with the quadratic residue technique attempts to break up primary clusters in a similar way, although it generates a probe sequence somewhat differently. The probe sequence for key k starts with h(k) and follows with
[h(k) + i2]mod m, [h(k) - i2]mod m for i = 1, 2, . . . , (m - 1)/2
Again, to ensure that m distinct indexes are generated, care must be taken in the choice of m. If m is prime and of the form (4 ?/FONT> j) + 3, then m distinct indexes are guaranteed. Since m = 23 in our example, j = 5 and (m - 1)/2 = 11. The probe sequence for key k is then
h(k),
[h(k) + 12] mod 23, [h(k) - 12] mod 23,
[h(k) + 22] mod 23, [h(k) - 22] mod 23, . . . ,
[h(k) + 112] mod 23, [h(k) - 112] mod 23
If k is 364, h(k) = 19, and the probe sequence is
19, 20, 18, 0, 15, 5, 10, 12, 3, 21, 17, 9, 6, 22, 16, 12, 1, 8, 7, 4, 11, 2, 13
This is really a secondary clustering technique, since keys that hash to the same address will still have identical probe sequences. The hash table for this technique appears as hash table (d) of Figure 9.4, which gives an average number of probes of 1/18 ?/FONT> [(10 ?/FONT> 1) + (4 ?/FONT> 2 ) + (3 ?/FONT> 3) + (1 ?/FONT> 4)] = 31/18 or 1.72 for a successful search. When a key is inserted with these secondary clustering techniques, the result may be the lengthening or connecting of two clusters. These events may occur simultaneously along more than one probe sequence when the key is inserted.
Returning to the example of the out-of-stock specialty item, we might look for a remedy that avoids even these secondary clusters, since they also tend to increase search and insertion times. It seems reasonable to try to disperse these secondary clusters by giving each would-be customer a seperate set of directions. This may be done by having store managers randomly select the next store for a customer to try. This idea is known as open addressing with double hashing. The technique uses a second hash function for p(k). To be most effective, this should be as "random" as the initial hash function and should assign a value to key k by selecting this value independently of the value assigned to key k by the initial hash function.
The theoretical analysis for this technique has not been carried out as fully as for other methods, but the results indicate that double hashing gives the best results among the open addressing techniques. Empirically, it gives results that are the same as those for "random" hashing (see Table 9.3). This is somewhat suprising, since random hashing corresponds to our store remedy. Double hashing, instead of picking a store randomly, over and over again, until a customer is satisfied, merely picks an individual displacement at random for each key. This displacement then determines the probe sequence for a given hash address.
Care must be exercised in the selection of the second hash function so that a desirable probe sequence is generated. If m is a prime, then one possibility that ensures the generation of such a probe sequence is
For instance, p(657) = 11, since 657 = 50 ?/FONT> 13 + 7 when m = 13. Hence the probe sequence for 657 is
7, 5, 3, 1, 12, 10, 8, 6, 4, 2, 0, 11, 9
Key 137 also has hash address 7, but p(137) = 10, since 137 = 10 ?/FONT> 13 + 7. Its probe sequence, however, is distinct from 657's:
7, 4, 1, 11, 8, 5, 2, 12, 9, 6, 3, 0, 10
Now, even keys with the same hash address are unlikely to have the same probe sequence. The idea is that, statistically, probe sequences should appear to be approximately independently and randomly generated for two distinct keys. The hash table produced by this technique is given as hash table (e) of Figure 9.4, and the average number of successful probes is 1/18 ?/FONT> [(11 ?/FONT> 1) + (4 ?/FONT> 2) + (2 ?/FONT> 3) + (1 ?/FONT> 4)] = 29/18 or 1.61
As a further illustration, suppose key 582 is to be inserted in the hash tables of Figure 9.4. Its hash address, 582 mod 23, is 7, since 582 = 25 ?/FONT> 23 + 7. The sequence of probed locations and the number of probes required for each table are given below.
It is interesting that the average number of probes required to make an insertion is the same as the average number of probes required to carry out an unsuccessful search. This fact is useful in the analysis of hashing. The results of the example are typical of the behavior of open addressing techniques. As the usage ratio of the table increases, the secondary clustering and quadratic residue methods provide considerable improvement over the primary clustering methods. The double hashing techniques improve the results even more. For lower usage ratios, the improvements are much less noticeable. These improvements in average numbers of probes do not translate directly into similar improvements in average times, which depend on implementation details.
Chaining is another method of collision resolution. The idea is to link together all records that collide at a hash address. These may be kept separately or within the hash table itself. Separate chaining treats each location of the hash table as the head of a list?/FONT>the list of all keys that collide at that location. Separate storage is used to store records of the list, which consist of key values and link pointer values. When a collision occurs, an insertion is made at the front of the corresponding list. Using this technique for our example yields the hash table shown in Figure 9.5 with corresponding numbers of probes (key comparisons). The table's average number of probes for a successful search is 1/18 ?/FONT> [(12 ?/FONT> 1) + (5 ?/FONT> 2) + (1 ?/FONT> 3)] = 25/18 or 1.39.
In contrast to open addressing, separate chaining allows clusters to form only when keys hash to the same address. Hence the lenghts of the lists should be similar to the lengths of clusters formed with secondary clustering techniques. A comparison of the 1.39 probes to the 1.89 or 1.72 probes with secondary clustering is somewhat unfair, since the hash table with separate chaining really uses additional storage. The actual amount of additional storage depends on the record lenghts. When they are small, and storage that would otherwise be unused is available for the link pointer values, then the usage ratio should more properly be measured as n/(n + m). This is 18/41, or 44 percent, in the example. When the link field takes up the same amount of storage as a record, then the usage ratio should more properly be measured as n/(2n + m). This is 18/59, or 31 percent, in the example.
Coalesced chaining maintains lists of records whose keys hash to the same address. These lists are stored within the hash table itself. Whenever two such lists "intersect," they coalesce. This is analogous to two separated clusters becoming connected when a new key is inserted in the location that separated them. Each hash table entry is now a record containing a key value and a link value to the next record on its associated list.
A key is inserted into the table by going to its hash address and traversing its list until a null key is found, the key itself is found, or no records remain on the list. If the null key is found, the new key is inserted in the record stored at that location, and its link field is set to null. If the key itself is found, no insertion is necessary. If no records remain on the list, then an unoccupied location must be found, the new key inserted there, and its link field set to null. This new record must then be appended at the end of the traversed list.
In order to create this new record to be appended, a pointer p is kept updated. Initially, p points to location m (which is just off the table). Whenever a new record must be found, p is decremented by 1 until the location it points to is unoccupied. If p "falls off" the table (becomes less than 0), then the table is full and no insertion is possible.
Figure 9.6 illustrates coalesced chaining for the example. P is initially 23 and the first four keys are inserted directly into their hash addresses. Key 663 collides at its hash address, 19. P is then decremented by 1 and, since location 22 is empty, 663 and a null next pointer are inserted there. This new record is then appended at the end of the list beginning in 19, by setting the link field of location 19 to 22. Key 262 is inserted directly into its hash address, 09. The next entry is 639, but its hash address, 18, contains an entry. P is then decremented by 1, and since location 21 is empty, 639 and a null link value is inserted there. This record is then appended at the end of the list beginning in 18 by setting the link field of location 18 to 21.
Figure 9.6 shows the resultant hash table, the number of probes for each key insertion, and the value of p after all eighteen keys are entered. The average number of probes for a successful search of this table is 1/18 ?/FONT> [(9 ?/FONT> 1) + (6 ?/FONT> 2) +(1 ?/FONT> 3) + (1 ?/FONT> 4) + (1 ?/FONT> 5)] = 33/18 or 1.81. If extra storage is available for the link fields, then n/m is a reasonable measure of the table usage here. These 1.81 probes are not as good as the 1.61 or 1.72 probes resulting from double hashing and quadratic residues in the example. Theoretical results, however, show that coalesced chaining does yield better average results than "random" hashing when storage is available for link pointer fields. You may expect coalesced chaining to give results that are not as good as separate chaining, better than linear or displaced linear probing, not as good as "random" or double hashing, but perhaps comparable to the secondary clustering techniques. If the link fields take additional storage, it should be taken into account in the usage factors for comparison. Note that coalesced chaining generally yields more but shorter lists (or clusters) than linear or displaced probing, because connecting or coalescing of clusters occurs to a lesser extent with coalesced chaining.
A third method of collision resolution will be discussed in Chapter 10 in connection with external memory, or secondary storage, where it is especially appropriate and useful.
Hash Hash Hash Hash Hash Hash
Keys Address Table (a) Table (b) Table (c) Table (d) Table (e)
-----------------------------------------------------------------------
019 19 0 802 (4) 663 (2) 364 (5) 364 (4) 392 (1)
392 01 1 392 (1) 392 (1) 392 (1) 392 (1)
179 18 2 364 (7)
359 14 3 321 (2)
663 19 4 364 (3) 566 (3)
262 09 5 097 (1) 097 (1) 097 (1) 097 (1) 097 (1)
639 18 6 720 (3) 260 (3) 663 (3)
321 22 7 720 (1) 720 (1) 639 (2) 720 (1) 720 (1)
097 05 8 468 (1) 468 (1) 468 (1) 468 (1) 468 (1)
468 08 9 262 (1) 262 (1) 262 (1) 262 (1) 262 (1)
814 09 10 814 (2) 976 (1) 976 (1) 814 (2) 976 (1)
720 07 11 260 (5) 260 (2) 976 (2) 364 (2)
260 07 12 976 (3) 566 (12) 814 (3) 321 (2)
802 20 13 814 (2) 566 (3)
364 19 14 359 (1) 359 (1) 359 (1) 359 (1) 359 (1)
976 10 15 774 (1) 774 (1) 774 (1) 774 (1) 774 (1)
774 15 16 566 (3) 566 (3)
566 14 17 260 (4) 639 (3) 260 (4)
18 179 (1) 179 (1) 179 (1) 179 (1) 179 (1)
19 019 (1) 019 (1) 019 (1) 019 (1) 019 (1)
20 663 (2) 802 (1) 663 (2) 663 (2) 806 (1)
21 639 (4) 802 (2) 802 (2) 814 (2)
22 321 (1) 639 (2) 321 (1) 321 (1) 639 (2)
linear displaced secondary quadratic double
probing linear clustering residue hashing
probing
Average number 2.22 2.00 1.89 1.72 1.61
of probes for a
succesful search
Figure 9.4 Typical Hash Tables for the Five Open-Addressing Techniques Considered (Usage Ratio 78 Percent)
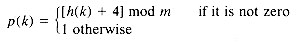

Linear probing 7, 8, 9, 10, 11, 12 (7)
Displaced linear
probing 7, 11, 15, 19, 0, 4, 8, 12, 16 (9)
Secondary
clustering 7, 18, 6, 17, 5, 16 (6)
Quadratic
residue 7, 8, 6, 11, 3 (5)
Double hashing 7, 9, 11, 13 (4)

Figure 9.5 Hash Table for Separate Chaining
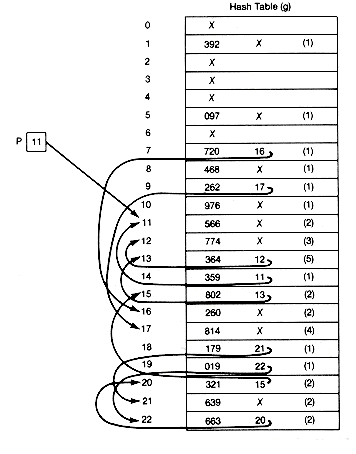
Figure 9.6 Hash Table for Coalesced Chaining