
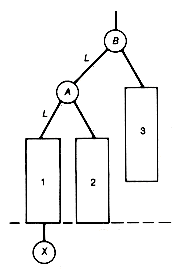
Consider the AVL tree of Figure 9.10(a). To insert a new record into this tree, let us first do a "simple" insertion. The dashed branches indicate the sixteen possible insertion positions for a new node. You should confirm that, of these, only an insertion of a new node as a successor of 45, 53, 81, or 100 will cause the new tree to fail to remain an AVL tree. An insertion at node 45 causes the subtrees with roots 55, 40, and 70 to become unbalanced. For example, the subtree with root 40 would have a left subtree of depth 3, while its right subtree would have depth 5. These differ by more than 1. Notice that 55, 40, and 70 lie along the search path from the root to the new node inserted as a successor of 45. If 43 were inserted, then the result would be the tree of Figure 9.10(b). Thus the "simple" insertion discussed earlier will not retain the balance of a search tree.
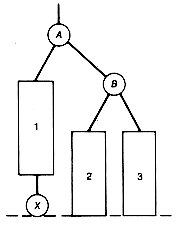
This imbalance is remedied by rearranging the subtree with root 55 as shown in Figure 9.10(c). Notice that the subtrees with roots 40 and 70 are no longer out of balance. In fact, the tree of Figure 9.10(c) is now an AVL tree. Notice also that the subtree in Figure 9.10(c) replacing the subtree of 55 in Figure 9.10(b) has exactly the same depth as the original subtree of 55 in Figure 9.10(a). If any of the other insertions that would have produced an imbalance in Figure 9.10(a) had occurred, they could have been remedied by similar rearrangements. You should confirm this by trying them all and finding the suitable rearrangements. Remember, the rearrangements must not only rebalance but also preserve the binary search tree property.
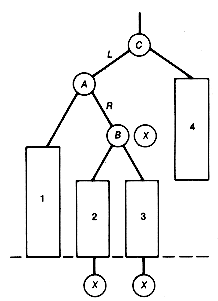
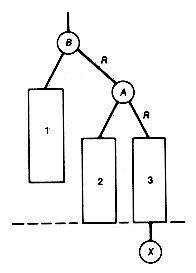
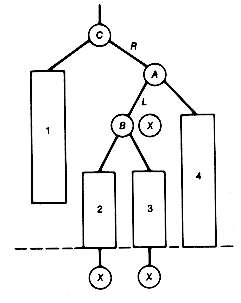
It is possible to analyze the general situation to determine exactly when an insertion will cause an imbalance and what its remedy will be. An insertion into an AVL tree with zero or one node cannot cause an imbalance. When the tree has more than one node, the types of imbalance, and their corresponding remedies, reduce to the four indicated in Figures 9.11 and 9.12.
Each rectangle in Figures 9.11 and 9.12 represents an AVL tree. Any of these may be null. An X represents the position of the inserted new record that has caused imbalance. Three X's appear in imbalances LR and RL, actually representing three possibilities, although only one will have taken place. The LR and RL imbalances are meant to include the special case where B is actually the inserted node. This is why the X appears next to node B. Subtrees 1, 2, 3, and 4 must then be null. This fact is noted here, since it is not clear from the figures. In cases LL and RR, the subtree with root B represents the node closest to the inserted node, along the path from the inserted node to the root, where an imbalance occurs. In cases LR and RL the subtree with root C represents this node. In all remedies, the subtrees represented by the rectangles retain their relative positions. Note that all remedies preserve the binary search tree property. It is very important to see that, in each case, the depth of the remedy is exactly the same as the depth of the original subtree before the new insertion was made. Consequently, no nodes on the path from the subtree root, B in cases LL and RR, and C in cases LR and RL, imbalanced by the new insertion, will be imbalanced after the remedy is applied. It is also important to see that these remedies are applied locally; they do not involve the creation of a new AVL tree in its entirety.

In Figure 9.11, when 43 was inserted, case LL occurred. The roles of B and A were taken by 55 and 50, respectively. The three rectangles, 1, 2, 3 of Figure 9.11 (a and b), represented, respectively, the subtrees shown in Figure 9.13. The X represented 43.
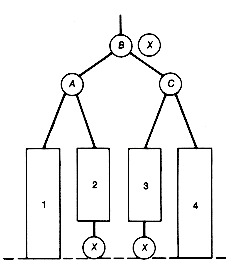
Consider imbalance LL. The remedy looks as though A has moved up to the root and B has moved to the right. This is called a rotation to the right of the subtree with B at its root. The remedy for imbalance RR would be described as a rotation to the left of the subtree with B at its root. To rectify imbalance LR, perform a rotation to the left of the subtree with root A to obtain Figure 9.14(a). A further rotation to the right of the subtree rooted at C produces (b) of Figure 9.14. Assume that rotations are accomplished by the procedures rotateleft and


rotateright, each with a parameter that points to the root of the subtree to be rotated. Then the remedies for each imbalance may be obtained by
LL: rotateright(plast) where last points to B
RR: rotateleft(plast) where last points to B
LR: rotateleft(p(last.leftptr)) where last points to C
rotateright(plast)
RL: rotateright(p(last.rightptr)) where last points to C
rotateleft(plast)
The procedure for rotateright, for example, might be as follows:
rotateright(plocalroot)
/* Performs a rotation to the right
of the subtree whose root is
pointed to by localroot.
*/
binarytreepointer *plocalroot;
{
binarytreepointer q;
q = (*plocalroot).leftptr;
(*plocalroot).leftptr = q?FONT FACE="Symbol" SIZE=2>>rightptr;
q->rightptr = *plocalroot;
*plocalroot = q;
}
Note that the procedure also changes the pointer in localroot, so it points to the root of the new subtree. It is assumed that nodes of the AVL tree are represented as follows:
typedef struct treenode
{
whatever key;
struct treenode *leftptr;
struct treenode *rightptr;
int balance;
}binarytreenode,*binarytreepointer;
The balance field stores the node's right subtree depth minus the node's left subtree depth. In an AVL tree it will have values - 1, 0, or + 1.
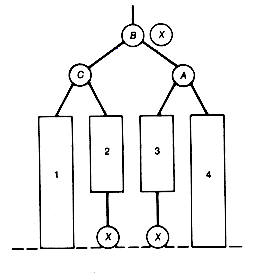
Consider the binary tree shown in Figure 9.15(a), which was balanced until the new node, marked by X, was inserted. The initial balance values are also shown. Because of the insertion, the root node and node C have become unbalanced. Since node C is closest to the inserted node, we remedy this imbalance by applying the remedy for RL to obtain Figure 9.15(b). The tree itself is now balanced, but the balances of nodes A, B, and C are now incorrect, as are the balances of the three nodes between X and A. The last node, however, does have the correct balance value.
In general, after rebalancing, one of the nodes involved in the remedy will be the new root of the subtree that was rebalanced (B in the example). If the remedy was LL or RR, all nodes along the path from this node to the inserted node, starting with its successor, need their balances reset. If the remedy was LR or RL, then all nodes along this path, starting with its successor's successor (the successor of A in the example), need their balances reset. The node not on this path involved in the remedy (C in the example) must have its balance reset, and, finally, the new root of the rebalanced subtree must have its balance set to 0. The special case when the inserted node is at B requires only that C's balance be set to 0. All nodes above this new root need not be reset; they retain their original values. Any time the root node is involved, special processing is required, since the head of the tree must be modified rather than a left or right subtree pointer of a node.
The algorithm for inserting a node into an AVL tree can now be written.
1. Search for the keyvalue.
2. If it is not found, then
a. Create a new node for it and set its field values.
b. Insert the new node into the tree.
c. If the tree has more than one node, then
If it is not necessary to rebalance, then reset last's balance and the balances of nodes on he search path between last and the new node.
If it is necessary to rebalance, then
i. apply the appropriate remedy to rebalance, reset the balance of the node involved in the remedy but not on the new search path, reset the proper new search path balances, set the balance of the root of the subtree at which rebalancing occurred to 0.
ii. If this root was the root of the tree itself, then
set the head of the tree to this root; otherwise
set its predecessor to this root;
else
reset the balance of the predecessor of the inserted node.
It has already been noted that, when rebalancing is necessary, once the subtree whose root is nearest the newly inserted node has been rebalanced with the correct remedy, all other subtrees along the path to the root of the entire tree will also be back in balance. Again, this is because the smallest subtree causing the imbalance has been modified by the remedy to have its original depth. All the subtrees were originally balanced when it had that depth, so they must be balanced now. During the search in step 1 for the insertion key, suppose you keep a pointer last. Last is updated to point to the node that may become imbalanced on the search path nearest the insertion node. Only nodes with balance values of + 1 or -1 may become imbalanced due to the insertion. It is necessary to rebalance only if last.balance was -1 and the search path went left at last, or last.balance was + 1 and the search path went right at last, and p is not t, and pred.balance = 0. Only nodes on the search path, between the inserted node and last, will need to have their balance fields updated.
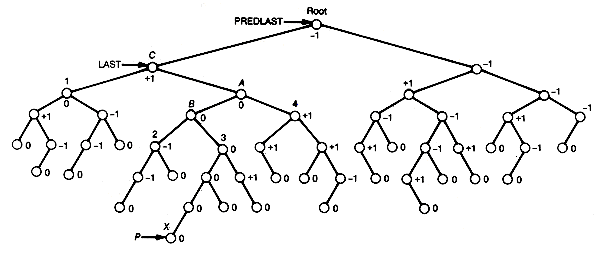
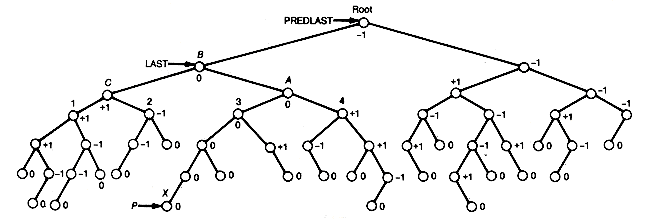
During the search, an updated pointer to the predecessor node of last should be kept in predlast. P will point to the node whose key field is currently being compared with the search key, and predp points to its predecessor. An implementation of the AVL tree insertion is given in the insertavl function. For clarity, the procedures createnode and search are then given separately, followed by procedures insertnode and resetpathbalances.
Nonrecursive AVL Insertion
As another illustration of recursion, a recursive version is presented next. It is based on the following formulation.
The recursive insertavl procedure is as follows:
Recursive AVL Insertion
In order to determine the balance of t upon return from the recursive calls (these are underlined in the algorithm), we will need to know if the subtree in which the node was inserted has increased in depth. A flag increase, with values 1 or 0, indicates an increase. Increase may be nonlocal to, or a parameter of, the function, but it must be initialized to 0 before the function is invoked. We make it a parameter.
The functions for resetting balances are
Suppose you wanted to create an AVL tree by reading a sequence of key values and to test the AVL insertion. The code below, when insertavl and the functions it invokes are included, creates the AVL tree using the recursive version of insertavl. It prints the key field values of the resultant tree nodes in preorder access order as the tree is created, and prints both the key and balance values in preorder access order for the final tree. The preorder traversal routine calls a process routine, as in Chapter 7, that prints out the key and balance field values of a node it is called to work on.
The function insertavl and all its invoked functions should go here, since they depend on the tree's implementation.
Notice that all components of the program except insertavl and its associated functions are written treating the binary tree as a data abstraction.
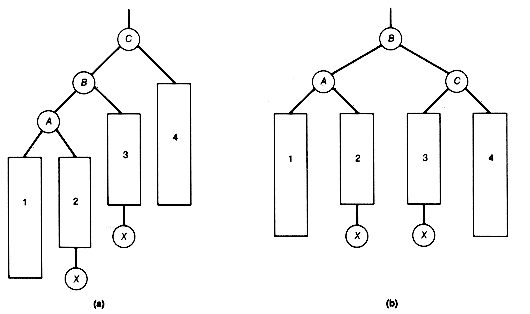
Deletion procedures for AVL trees are not developed in detail here, but the basic ideas will be illustrated. Consider the AVL tree of Figure 9.16(a). The tree is a Fibonacci tree of depth 5. Suppose the rightmost node of its right subtree, 12, is deleted, as in a simple binary search tree. The result is Figure 9.16(b).
Node 11, the predecessor of 12, is now unbalanced. Rebalancing can be achieved by applying remedy LR at node 11 to obtain Figure 9.16(c). Node 8, the predecessor of 11 before rebalancing, is now unbalanced. Rebalancing can be done by applying remedy LL at node 8 to obtain Figure 9.16(d).
This tree is finally an AVL tree. Deleting the rightmost node from any such Fibonacci tree will always lead to a rebalancing at every node along the search path.
The basic algorithm for deletion of a node from an AVL tree is first to delete, as in a simple binary tree. Then the search path must be retraced, from the deleted node back to the root. If an imbalance occurs, it must be remedied. Deletion can require O(1g n) rebalances, while insertion can require at most one rebalance.
A recursive deletion algorithm is sketched below.
#define TRUE 1
#define FALSE 0
#define NULL 0
insertavl(keyvalue,pt)
/* Inserts a new record with key equal to
keyvalue in the AVL tree t, if a record
with this keyvalue is not present in t.
After insertion t will still be an AVL tree.
*/
whatever keyvalue;
binarytreepointer *pt;
{binarytreepointer p,predp,last,predlast,q;
int found;
search(keyvalue,*pt,&p,&predp,
&last,&predlast,&found);
if(!found)
{createnode(keyvalue,&p);
insertnode(keyvalue,p,predp,pt);
if(p != *pt)
if(predp->balance == 0)
if(keyvalue < last->key)
if(last->balance == 0)
{last->balance = -1;
resetpathbalances(keyvalue,
last->leftptr,p);
}
else if(last->balance == +1)
{last->balance = 0;
resetpathbalances(keyvalue,
last?gt;leftptr,p);
}
else
{q = last->leftptr;
if(keyvalue < q->key)
ll(keyvalue,&last,p);
else
lr(keyvalue,&last,&q,p);
last->balance = 0;
if(predlast == NULL)
*pt = last;
else if(keyvalue < predlast->key)
predlast->leftptr = last;
else
predlast->rightptr = last;
}
else
if(last->balance == 0)
{last->balance = +1;
resetpathbalances(keyvalue,
last->rightptr,p);
}
else if(last->balance == -1)
{last->balance = 0;
resetpathbalances(keyvalue,
last->rightptr,p);
}
else
{q = last->rightptr;
if(keyvalue < q->key)
rr(keyvalue,&last,p);
else
rl(keyvalue,&last,&q,p);
last->balance = 0;
if(predlast == NULL)
*pt = last;
else if(keyvalue < predlast->key)
predlast->leftptr = last;
else
predlast->rightptr = last;
}
else
predp->balance = 0;
}
}
ll(keyvalue,plast,p)
/* Applies remedy ll, resets the balance of the node
involved in the remedy but not on the new search
path, and resets the proper new search path balances.
*/
whatever keyvalue;
binarytreepointer *plast,p;
{rotateright(plast);
((*plast)->rightptr)->balance = 0;
resetpathbalances(keyvalue,(*plast)->leftptr,p);
}
lr(keyvalue,plast,pq,p)
/* Applies remedy lr, resets the balance of the node
involved in the remedy but not on the new search
path, and resets the proper new search path balances.
*/
whatever keyvalue;
binarytreepointer *plast,*pq,p;
{rotateleft(&((*plast)->leftptr));
rotateright(plast);
if(keyvalue < (*plast)->key)
{(*pq).balance = 0;
((*plast)->rightptr)->balance = +1;
resetpathbalances(keyvalue,
((*plast)->leftptr)->rightptr,p);
}
else if(keyvalue > (*plast)->key)
{(*pq)->balance = -1;
((*plast)->rightptr)->balance = 0;
resetpathbalances(keyvalue,
((*plast)->rightptr)->leftptr,p);
}
else
((*plast)->rightptr)->balance = 0;
}
rr(keyvalue,plast,p)
/* Applies remedy rr, resets the balance
of the node involved in the remedy but
not on the new search path, and resets
the proper new search path balances.
*/
whatever keyvalue;
binarytreepointer *plast,p;
{rotateleft(plast);
((*plast)->leftptr)->balance = 0;
resetpathbalances(keyvalue,(*plast)->rightptr,p);
}
rl(keyvalue,plast,pq,p)
/* Applies remedy rl, resets the balance
of the node involved in the remedy but
not on the new search path, and resets
the proper new search path balances.
*/
whatever keyvalue;
binarytreepointer *plast,*pq,p;
{rotateright(&((*plast)->rightptr));
rotateleft(plast);
if(keyvalue > (*plast)->key)
{(*pq)->balance = 0;
((*plast)->leftptr)->balance = -1;
resetpathbalances(keyvalue,((*plast)->rightptr)->leftptr,p);
}
else if(keyvalue < (*plast)->key)
{(*pq)->balance = +1;
((*plast)->leftptr)->balance = 0;
resetpathbalances(keyvalue,((*plast)->leftptr)->rightptr,p);
}
else
((*plast)->leftptr)->balance = 0;
}
rotateright(plocalroot)
/* Performs a rotation to the right
of the subtree whose root is
pointed to by localroot.
*/
binarytreepointer *plocalroot;
{binarytreepointer q;
q = (*plocalroot)->leftptr;
(*plocalroot)->leftptr = q->rightptr;
q->rightptr = *plocalroot;
*plocalroot = q;
}
rotateleft(plocalroot)
/* Performs a rotation to the left
of the subtree whose root is
pointed to by localroot.
*/
binarytreepointer *plocalroot;
{binarytreepointer q;
q = (*plocalroot)->rightptr;
(*plocalroot)->rightptr = q->leftptr;
q->leftptr = *plocalroot;
*plocalroot = q;
}
resetpathbalances(keyvalue,start,p)
/* Resets the balances of all nodes on
search path between the nodes
pointed to by start and p.
*/
whatever keyvalue;
binarytreepointer start,p;
{binarytreepointer q;
q = start;
while(q !=p)
if(keyvalue < q->key)
{q-balance = -1;
q = q->leftptr;
}
else
{q->balance = +1;
q = q->rightptr;
}
}
createnode(keyvalue,pp)
/* Returns with p pointing to a new node
record with key equal to keyvalue,
left and right pointer fields null, and
balance field zero.
*/
whatever keyvalue;
binarytreepointer *pp;
{*pp = malloc(sizeof(binarytreenode));
(*pp)->key = keyvalue;
(*pp)->leftptr = NULL;
(*pp)->rightptr = NULL;
(*pp)->balance = 0;
}
search(keyvalue,t,pp,ppredp,plast,ppredlast,pfound)
/* Returns with found true only if the binary search
tree t has a node with its key equal to keyvalue.
If found is true
p and predp point respectively, to
the found node and its predecessor,
else
predp, and last, will point, respectively,
to the node that will be the new node's
predecessor, and the node along the search
path closest to the new node's insertion point
that may become unbalanced.
*/
whatever keyvalue;
binarytreepointer t,*pp,*ppredp,*plast,*ppredlast;
int *pfound;
{*pfound = FALSE;
*pp = t;
*plast = t;
*ppredp = NULL;
*ppredlast = NULL;
while((*pp != NULL) && (!*pfound))
if(keyvalue < (*pp)->key)
{if((*pp)->balance != 0)
{*ppredlast = *ppredp;
*plast = *pp;
}
*ppredp = *pp;
*pp = (*pp)->leftptr;
}
else if(keyvalue > (*pp)->key)
{if((*pp)->balance != 0)
{*ppredlast = *ppredp;
*plast = *pp;
}
*ppredp = *pp;
*pp = (*pp)->rightptr;
}
else
*pfound = TRUE;
}
insertnode(keyvalue,p,predp,pt)
/* Inserts the new node, pointed to
by p, as the proper successor
of predp.
*/
whatever keyvalue;
binarytreepointer p,predp,*pt;
{if(predp == NULL)
*pt = p;
else
if(predp == *pt)
if(keyvalue < (*pt)->key)
(*pt)->leftptr = p;
else
(*pt)->rightptr = p;
else
if(keyvalue < predp->key)
predp->leftptr = p;
else
predp->rightptr = p;
}
To insert a node in t:
If t is null then
create the new node, set its field values and set t to it
else
if keyvalue < t.key, then
insert the node in t.leftptr
if t is balanced, then
reset its balance
else
rebalance t and reset the balances of the nodes involved in the
remedy
else if keyvalue > t.key then
insert the node in t.rightptr
if t is balanced, then
reset its balance
else
rebalance t and reset the balances of the nodes involved in the
remedy.
#define TRUE 1
#define FALSE 0
#define NULL 0
insertavl(keyvalue,pt,pincrease)
/* Inserts a new record with key value to
keyvalue in the AVL tree t, if a record
with this keyvalue is not present in t.
After insertion t will still be an AVL tree.
Increase must be zero when the function is invoked.
*/
whatever keyvalue;
binarytreepointer *pt;
int *pincrease;
{binarytreepointer q;
if(*pt == NULL)
{createnode(keyvalue,pt);
*pincrease = 1;
}
else if(keyvalue < (*pt)->key)
{insertavl(keyvalue,
&((*pt)->leftptr),pincrease);
if(*pincrease) == 1)
if((*pt)->balance == 0)
(*pt)->balance = -1;
else if((*pt)->balance == +1)
{(*pt)->balance = 0;
*pincrease = 0;
}
else
{q = (*pt)->leftptr;
if(keyvalue < q->key)
ll(pt);
else
lr (pt,q);
(*pt)->balance = 0;
*pincrease = 0;
1 t's depth did not increase
}
}
else if(keyvalue > (*pt)->key)
{insertavl(keyvalue,
&((*pt)->rightptr),pincrease);
if(*pincrease == 1)
if((*pt)->balance == 0)
(*pt)->balance = +1;
else if((*pt)->balance == -1)
{(*pt)->balance = 0;
*pincrease = 0;
}
else
{q = (*pt)->rightptr;
if(keyvalue > q->key)
rr (pt)
else
rl(pt,q);
(*pt)->balance = 0;
*pincrease = 0;
}
}
}
ll(pt)
/* Apply remedy ll and reset the
balance of the node involved in
the remedy.
*/
binarytreepointer *pt;
{rotateright(pt);
reset1balance((*pt)->rightptr);
}
lr(pt,q)
/* Apply remedy lr and reset the balances
of the two nodes involved in
the remedy.
*/
binarytreepointer *pt,q;
{rotateleft(&((*pt)->leftptr));
rotateright(pt);
reset2balances(q,*pt,(*pt)->rightptr);
}
rr(pt)
/* Apply remedy rr and reset the
balance of the node involved in
the remedy.
*/
binarytreepointer *pt;
{rotateleft(pt);
reset1balance((*pt)->leftptr);
}
rl(pt,q)
/* Apply remedy rl and reset the balances
of the two nodes involved in the remedy.
*/
binarytreepointer *pt,q;
{rotateright(&((*pt)->rightptr));
rotateleft(pt);
reset2balances(q,*pt,(*pt)->leftptr);
}
rotateright(plocalroot)
/* Performs a rotation to the right
of the subtree whose root is
pointed to by localroot.
*/
binarytreepointer *plocalroot;
{binarytreepointer q;
q = (*plocalroot)->leftptr;
(*plocalroot)->leftptr = q->rightptr;
q->rightptr = *plocalroot;
*plocalroot = q;
}
rotateleft(plocalroot)
/* Performs a rotation to the left
of the subtree whose root is
pointed to by localroot.
*/
binarytreepointer *plocalroot;
{binarytreepointer q;
q = (*plocalroot)->rightptr;
(*plocalroot)->rightptr = q->leftptr;
q->leftptr = *plocalroot;
*plocalroot = q;
}
createnode(keyvalue,pp)
/* Returns with p pointing to a new node
record with key equal to keyvalue,
left and right pointer fields null, and balance field zero.
*/
whatever keyvalue;
binarytreepointer *pp;
{*pp = malloc(sizeof(binarytreenode));
(*pp)->key = keyvalue;
(*pp)->leftptr = NULL;
(*pp)->rightptr = NULL;
(*pp)->balance = 0;
}
reset1balance(q)
/* Sets the balance of node
q to zero.
*/
binarytreepointer q;
{q->balance = 0;
}
reset2balances(q,t,p)
/* Resets the balance of nodes
p and q determined by the
balance of t.
*/
binarytreepointer q,t,p;
{if(t->balance == -1)
p->balance = +1;
else
p->balance = 0;
if(t->balance == +1)
q->balance = -1;
else
q->balance = 0;
}
#include <stdio.h>
#define NULL 0
typedef int whatever;
typedef struct treenode
{whatever key;
struct treenode *leftptr;
struct treenode *rightptr;
int balance;
}binarytreenode,*binarytreepointer;
binarytreepointer left(p)
/* Returns a copy of the left pointer
of the node pointed to by p.
*/
binarytreepointer p;
{return(p->leftptr);
}
binarytreepointer right(p)
/* Returns a copy of the right pointer
of the node pointed to by p.
*/
binarytreepointer p;
{return(p->rightptr);
}
info(l)
/* Returns the key field value of
the node pointed to by l.
*/
binarytreepointer l;
{return(l->key);
}
bal(l)
/* Returns the balance field value of
the node pointed to by l.
*/
binarytreepointer l;
{return(l->balance);
}
binarytreepointer setnull()
/* Returns a null pointer. */
{return(NULL);
}
#define SENTINEL -1
main()
/* Reads record information, creates an AVL tree
storing the records, prints the key field values
of the tree records in preorder access order
after each record is inserted in the tree, and
prints the key & balance field values of the
final tree in preorder access order.
*/
{binarytreepointer t,setnull();
int keyvalue,increase;
t = setnull();
printf(\" enter keyvalue or sentinel \n");
scanf("%d",&keyvalue);while(keyvalue != SENTINEL)
}
increase = 0;
insertavl(keyvalue,&t,&increase);
printf("\n enter keyvalue or sentinel \n");scanf("%d",&keyvalue);printtree(t);
}
preorder (t);
}
printtree(t)
/* Prints the keys of t in
preorder access order.
*/
binarytreepointer t,left(),right();
{printf("\n %d \n",info(l));printtree(left(t));
printtree(right(t));
}
preorder(t)
/* Prints the keys & balances of
t in preorder access order.
*/
binarytreepointer t,left(),right(),setnull();
{if(t == setnull())
printf("\n The tree is null \n");else
{process(t);
preorder(left(t));
preorder(right(t));
}
}
process(t)
/* Prints the key and balance fields of
the node pointed to by t.
*/
binarytreepointer t;
{printf("\n key:%d balance:%d \n",info(t),bal(t));}
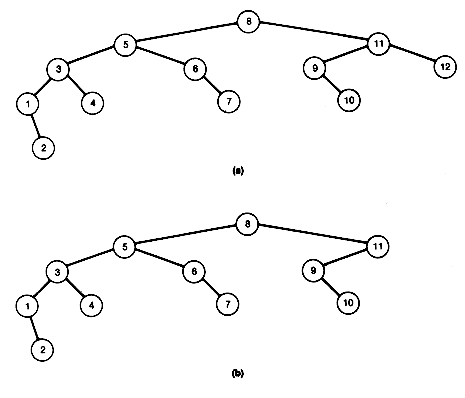
Figure 9.16 A Fibonacci Tree of Depth 5 and Deletion
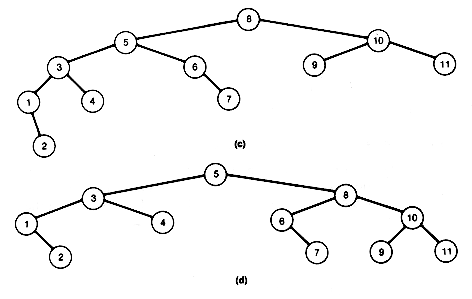
Figure 9.16
To delete a node from t:
If t is not null, then
if keyvalue<t.key, then
delete the node from t.leftptr
if t is balanced, then
reset its balance
else
rebalance t and reset balances
else if keyvalue>t.key, then
delete the node from t.rightptr
if t is balanced, then
reset its balance
else
rebalance t and reset balances
else
delete the node with the largest key value in t.leftptr
replace the root of t by that deleted node
if t is balanced, then
reset its balance
else
rebalance t and reset balances.